Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
This chapter includes an accompanying lecture presentation that has been prepared by the author: ![]() .
.
The ability of diffusion tensor imaging (DTI) tractography to depict eloquent white matter structures such as the pyramidal tract, arcuate fasciculus, and optic radiation (geniculocalcarine tract) has reduced surgical morbidity and supported improved extent of resection for brain tumors.
Longitudinal studies have shown that the accumulation of successive head injuries by athletes correlates with losses in DTI fractional anisotropy (FA) that match with functional impairments in postconcussive individuals. For athletes commencing impact sports, a preinjury DTI scan greatly improves the diagnostic value of subsequent DTI imaging. FA is generally subject to statistical analysis regarding the presence or absence of injuries to specific tracts by right-left comparison and by comparison to data on control subjects.
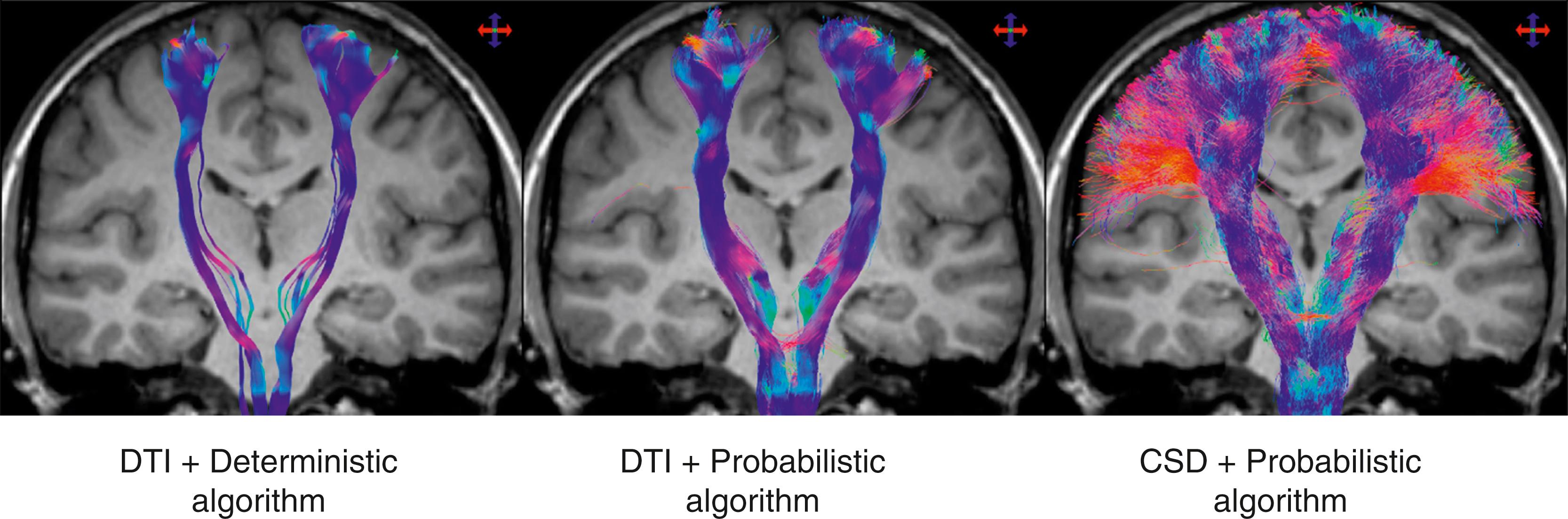
The Human Connectome Project has resulted in dramatic further advancements in the complexity and detail of tractography, while generally abandoning the tensor model in favor of newer mathematical models such as constrained spherical deconvolution (CSD).
Specific injuries identifiable with DTI—such as a damage to the fornix—can be identified to explain specific functional deficits such as impairment of new memory formation or damage to the angular gyrus resulting in problems with word finding after head injury.
Tractographic imaging provides an increased access to critical targets for functional neurosurgery both for lesioning and for stimulation.
DTI is based on special MRI pulse sequences that allow pulsed magnetic field diffusion gradients to be applied in multiple directions without disrupting the x, y, and z gradients that make imaging possible. The resulting data are then processed with tensor or advanced vector mathematics to calculate the direction or directions of axons in each image voxel.
The advent of imaging methods that measure and depict directional diffusion in neural tissue have revolutionized neuroscience and continue to have a progressively transformative impact in several subdisciplines of neurosurgery. Tractography based on diffusion anisotropy imaging has become critical to surgical planning for surgical treatments for brain tumors, epilepsy, and trauma, as well as for functional treatments that require highly targeted lesioning or deep brain stimulation targeting ( Fig. 14.1 ). Applications in evaluating spinal cord pathology and peripheral nerve disorders are advancing as well. Early localization of areas of ischemia and occult stroke has also emerged as an important new application of this technology and has the potential to enable better understanding of recovery or progression after an initial ischemic event.
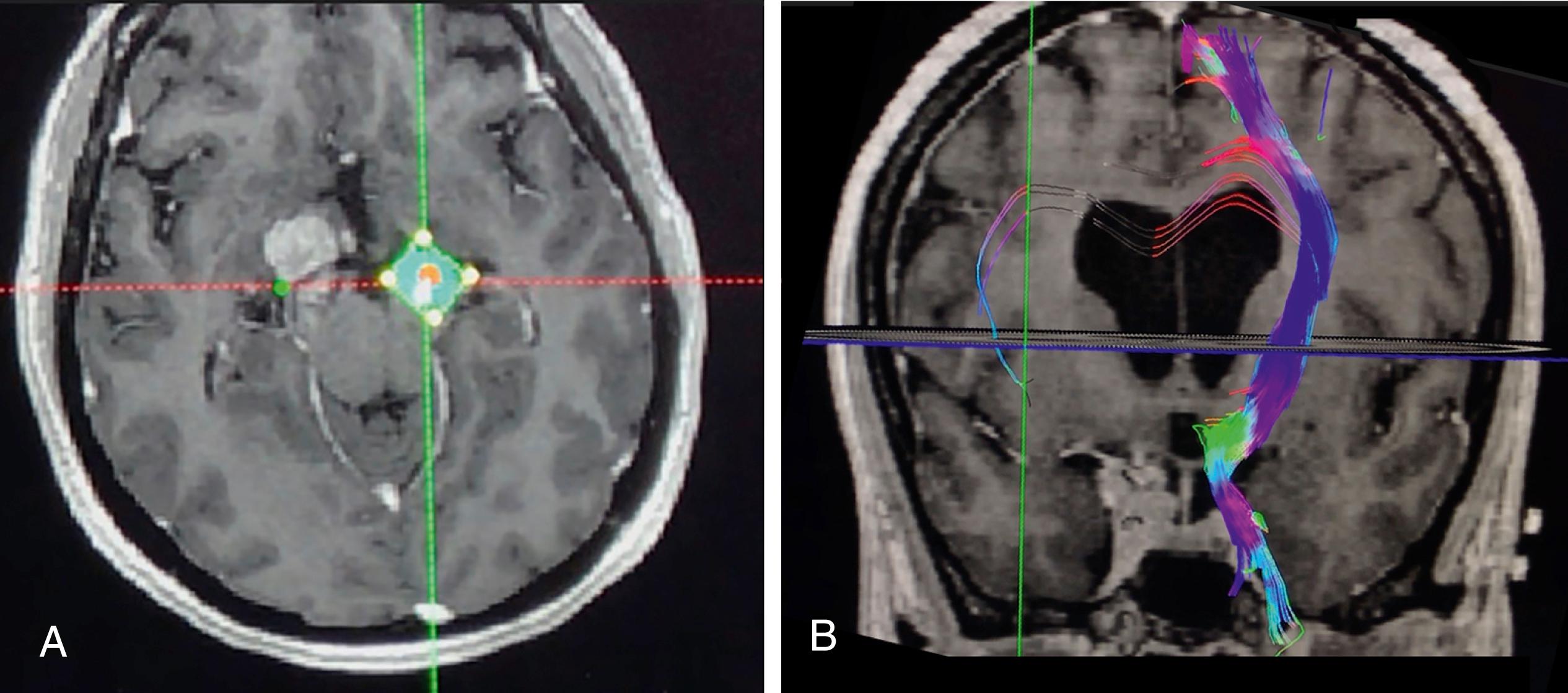
Diffusion tensor imaging (DTI) tractography is now increasingly deployed for complex surgical planning tasks in aneurysm surgery, approaches to arteriovenous malformations, and for assessment of effects of vasospasm in subarachnoid hemorrhage. Developing procedural treatments for psychiatric disorders and planning for neuroendoscopy , are other areas that reach beyond the longstanding role of DTI tractography in neuro-oncology.
In tumor surgery, the potential to have a detailed view of the pyramidal tract, the arcuate fasciculus and the optic radiations and other critical white matter pathways as they traverse the centrum semiovale has greatly increased the safety of many surgeries. In 2007 Wu et al. reported from a randomized controlled prospective study of 260 glioma operations that the use of tractography led to a 43% decrease in surgically related mortality and a 62% decrease in surgical morbidities such as unnecessary paralysis, muteness, and blindness.
The field continues to advance rapidly with the advent of remarkably high resolution from new 7-Tesla imagers and similar advances based on technologic advances applied in advanced 3-T systems. Advances in analytic methodology also continue at a rapid pace. ,
The introduction of this technology arose from a single key breakthrough invention, which, once accomplished, led rapidly to the production of the first tractogram over a matter of weeks. The initial published report of the critical advance in MRI physics that makes the entire field possible was the September 1992 publication by Franklyn Howe (an MR physicist with a doctorate from Oxford) and Aaron Filler (a neurosurgery resident at the University of Washington who commenced the research during his doctoral work at Harvard), which revealed that they had solved the problem of how to direct an off-angle diffusion gradient through the location gradients required for MRI without causing the destructive cross-term interactions that had stymied all other researchers in this field. A number of groups were racing to find a way to make the first diffusion anisotropy image, and by 1991 all had identified the seemingly insoluble problem of destructive cross terms destroying the image. , After this first fundamental discovery, the subsequent steps that that led to the production of the first tractogram in early 1992 occurred over a matter of just a few weeks.
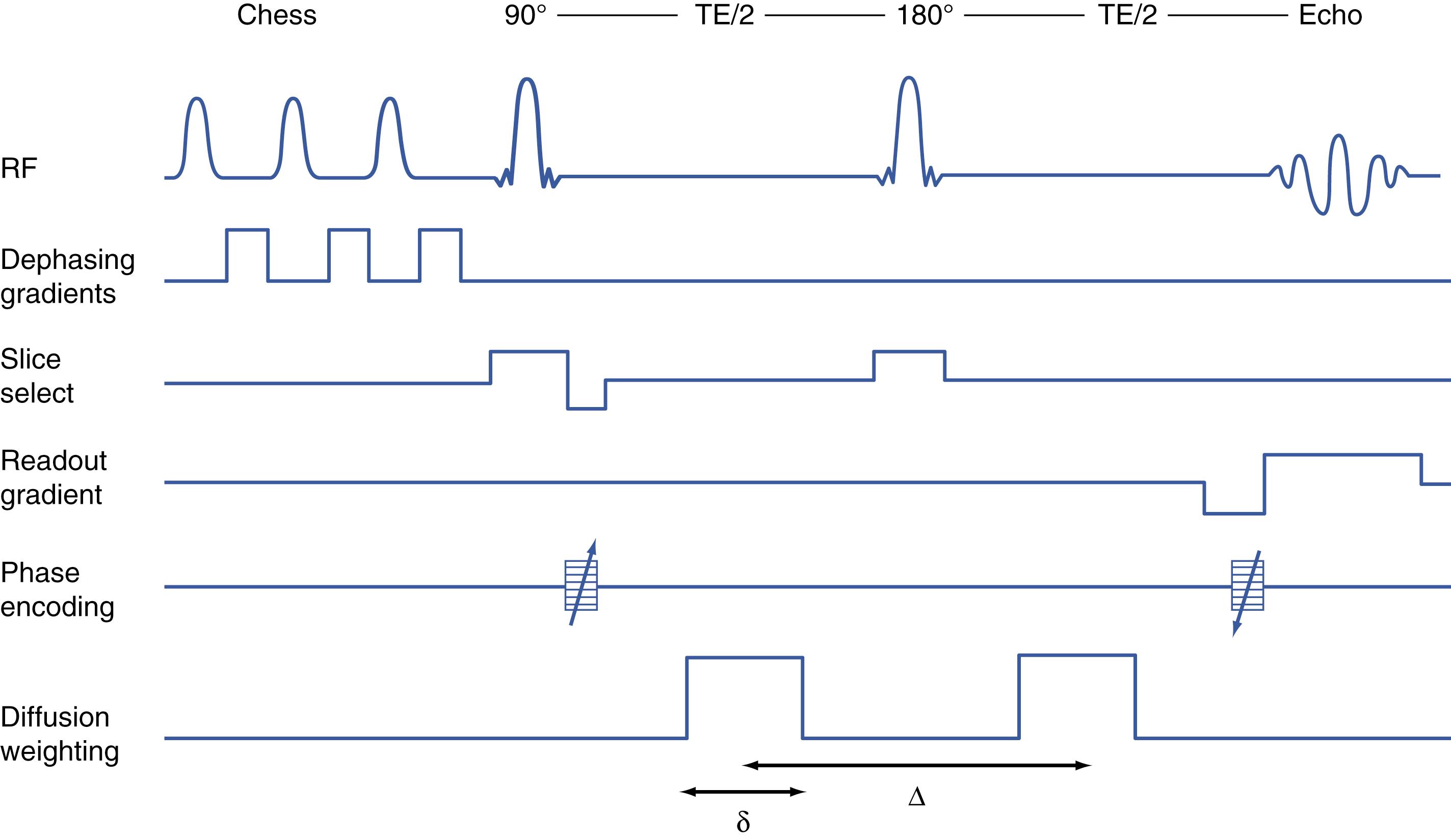
The discovery was in the field of MRI pulse sequence technology. Spin echo MRI uses a method called a 180-degree inversion pulse to eliminate noise and refocus the image signal of spinning protons ( Fig. 14.2 ). Howe and Filler showed that the same inversion pulse could be used to untangle the chaos that resulted when a powerful diffusion gradient magnetic field was directed through the delicate magnetic field array of the x, y, and z direction gradients required by all MRI. If the location gradient that was activated closest in time to the diffusion gradient was split into two oppositely directed pulses equally timed in opposite directions a few milliseconds before and a few milliseconds after the inversion pulse, then the destructive cross terms would disappear. When this critical innovation was tested and proven to work, the first diffusion image from an off-angle diffusion gradient was thus obtained, and this was reported in the 1992 publication along with the pulse sequence ( Fig. 14.3 ). This fundamental method, which also appeared in the Filler et al. patent application that led to US patent number 5,560,360 (initial filing in March 1992), is used to this day in every DTI, Q-Ball, high angular resolution diffusion imaging (HARDI), or other diffusion anisotropy image. The method is also called a “single-shot” method because the destructive cross terms are applied and then cancelled in a few milliseconds within a single pulse sequence acquisition.
The next step in the development of DTI was to show that diffusion-related MRI could in fact detect directional structure in brain tissue as the inventors had anticipated when multiple directions of off-angle diffusion gradients were used and a mathematical calculation of a vector or tensor direction was made in each voxel—a method developed with regard to vectors by Todd Richards (one of the US patent number 5,560,360 co-inventors from the University of Washington) and extended to tensors by Filler.
The final step was to apply the connected voxel algorithms that had been used for MR angiography to the directional information in each voxel so that selected white matter tracts could be visualized by starting at a seed location and using the orientation data to march along from voxel to voxel with a result that shows the actual white matter tracts in the brain in a way that could be captured in a medical image. This was developed by Jay Tsuruda (a neuroradiologist who is a coauthor of Moseley’s seminal 1990 paper ), the fourth of the University of Washington US patent number 5,560,360 inventors in further work with Filler. These original discoveries that underlie the technology were made 30 years ago. There are now more than 20,000 peer-reviewed publications in this field, and the pace of research and optimization continues to progress.
This work emerged from two groups working in this area during 1991 and 1992 on the fundamental method of data acquisition for DTI—one team led by neurosurgical resident Aaron Filler and colleagues at the University of Washington (Todd Richards and Jay Tsuruda) and University of London (Franklyn Howe) , and, separately, a second team led by Peter Basser and Dennis Le Bihan at the National Institutes of Health (NIH). In 1994 Peter Basser, an engineer, and Denis Le Bihan, a physician with training in neurosurgery and radiology, along with James Mattiello, a medical physicist, published a critical foundational paper in this field setting forth the mathematical basis for the design of the imaging method. The first pyramidal tract tractogram image from the Filler group was published in 1996 (filed in 1993) and the first from the Basser group, with Carlo Pierpaoli, appeared in 2000.
Both Filler and Basser were involved in strain gauge mathematics at Harvard University in the early 1980s—Basser as an undergraduate and Filler as a graduate student. This was one of two areas in which tensor mathematics was applied at Harvard’s Museum of Comparative Zoology (Functional Morphology group) and Department of Anthropology. , The application of the tensor method in structural and functional biology was taught by Filler and others as part of Harvard’s Biology 21 course. Filler also worked with Terrence Deacon doing axonal transport tracer studies to study the anatomy of the arcuate fasciculus in primates and for peripheral nerve imaging. Filler had been applying multivariate mathematics for analysis of brain anatomy dating back to a bachelor’s thesis at the University of Chicago in 1977.
In 1990 Lisa Tauxe, , , working with David Pilbeam’s team at the Department of Anthropology at Harvard, published an application of tensor mathematics for use in the field of magnetic stratigraphy—the use of changes in the direction of the earth’s magnetic field to identify stratigraphic layers. This was to support efforts to provide dates for hominoid fossils from the Miocene era (12 million years ago) in the Siwalik mountains of Pakistan. In the method, magnetometer data were collected from six different directions for each rock sample, so that a tensor could be determined that showed the orientation of the magnetic field in each sample. Numerous samples were collected, their orientation was noted when they were collected, and then each was subjected to tensor analysis from multiple directions so that magnetic flux stratigraphic lines in the mountainside could be determined.
Filler was a graduate student and lecturer in this research group (1979–1984), but later applied this exact mathematical paradigm to axonal directions to determine tracts in the brain, along with colleagues Todd Richards, an MR physicist who created software to determine the vector array for the brain; Franklyn Howe, who designed MRI pulse sequences capable of acquiring the data; and Jay Tsuruda, a neuroradiologist who showed how to postprocess the image data to depict the tracts. Both Tsuruda and Richards had trained under Michael Moseley, who introduced diffusion-weighted imaging (DWI) to brain imaging in 1990. ,
Filler, who in 1990 was a fourth-year resident in neurosurgery at the University of Washington under H. Richard Winn, filed a National Research Service Award (NRSA) grant application for a new method of MRI with off-angle gradients for anisotropic diffusion imaging in May 1991. This was rejected by NIH in October 1991 on the grounds that (1) the project was just about developing a method and had not focused on any one specific neurological hypothesis and (2) Filler had been unable to identify any experienced supervisor in this field (a field that had not yet come into existence).
Filler was seconded to London to work as a neurosurgery registrar at Atkinson Morley’s Hospital in Wimbledon—the site where Hounsfield invented and built the first CT scanner. In light of the NIH grant rejection, the consultant neurosurgery staff of Atkinson Morley’s Hospital—David Uttley, Anthony Bell, Henry Marsh, and Anne Moore—decided to put up funds from the hospital research foundation to support the project. When the project succeeded, Filler gave the first report of the new advance in imaging axonal flow by MRI at a joint meeting of the Society of British Neurological Surgeons and the New England Neurosurgical Society at a September 19, 1991 conference at the National Hospital for Neurology and Neurosurgery at Queen Square in London.
Peter Basser came to NIH in 1991 as an engineer working on strain gauges and magnetic stimulation of nerves, with no involvement or background in medical imaging. In September 1991, he came across a poster from another NIH scientist, Denis Le Bihan, showing early work in MRI of diffusion anisotropy. Basser realized that the tensor formalism he had learned as a student at Harvard could be applied to solve part of the imaging problem that Le Bihan was struggling with. On November 11, 1991, he wrote a confidential letter to several colleagues proposing the mathematical tensor solution to determining the orientation of diffusion in a voxel in MRI, essentially applying the same mathematics in which both Filler and he had been trained by the same sources at Harvard.
Filler, Howe, Richards, and Tsuruda—the four inventors on the Seattle/London patent—had poster presentations at the International Society for Magnetic Resonance in Medicine meeting in Berlin in August 1992; Basser, Le Bihan, and Mattiello had their poster in the same hall at the same meeting. Michael Moseley, one of the leading diffusion MRI scientists, saw the posters from Filler, Howe, Richards, and Tsuruda in Berlin, obtained copies of their images from them, and presented the work as part of a plenary session for the annual meeting of the Society for Magnetic Resonance Imaging in San Francisco in March 1993 in front of hundreds of MRI scientists. Denis Le Bihan was the moderator of the San Francisco session. The Seattle/London patent was filed in March 1993 as well, and subsequently Basser, Le Bihan, and Mattiello filed their patent in August 1993.
However, despite filing a patent, neither Basser nor Le Bihan knew how to collect the off-angle diffusion data necessary to actually make the image. Filler and Howe solved this problem and generated the first image data.
Richards wrote a program in Fortran on a Mac computer that took the diffusion data and then performed the voxel-by-voxel calculation on an actual brain MRI image data set to determine a mathematical summary of neural direction in each voxel of a brain image. Tsuruda showed how to generate a pyramidal tract tractogram from Todd Richard’s data by mathematically marching from voxel to voxel, and the result of the work by the four inventors is Figure 17 in US patent number 5,560,360—a patent with initial filings in the United Kingdom in March 1992 and completed filing in the United States in March 1993 ( Fig. 14.4 ).
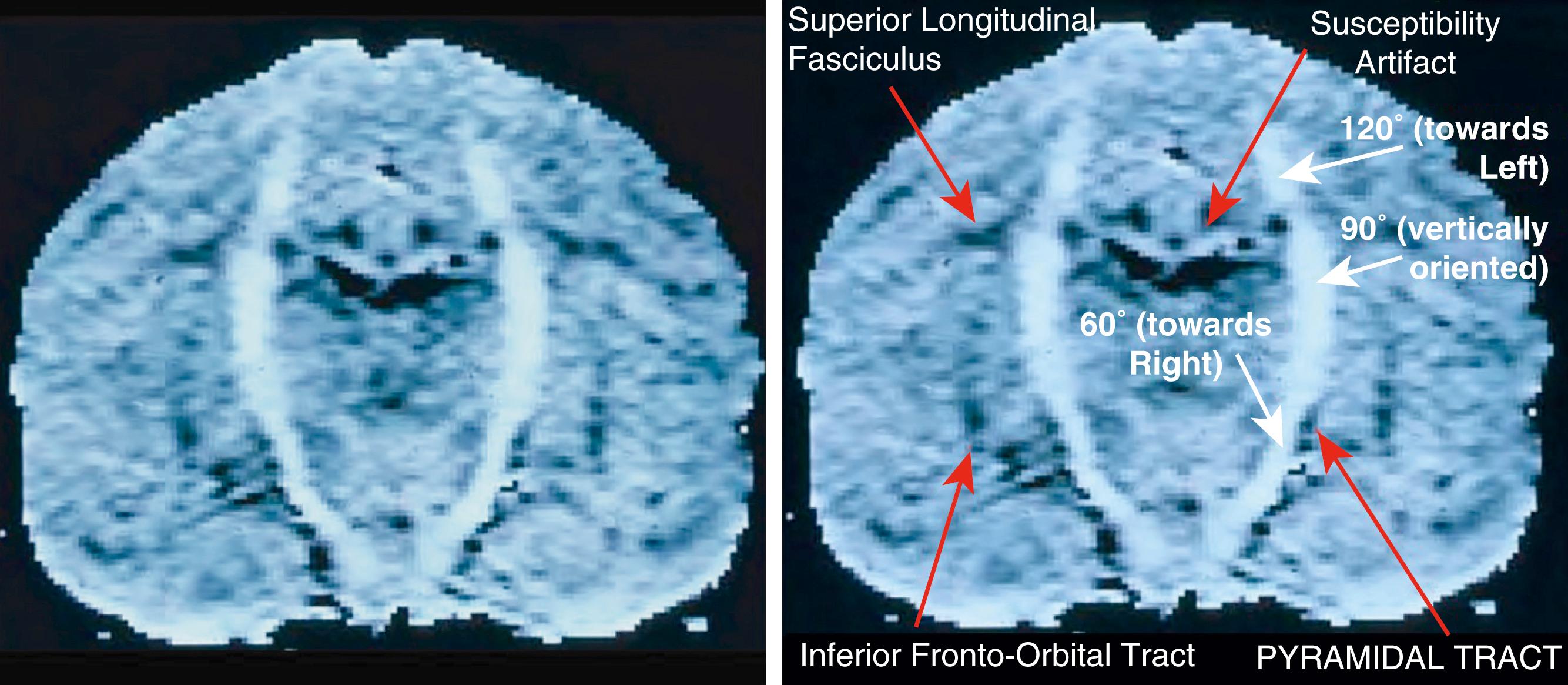
Basser, Mattielo, and Le Bihan filed their patent in August 1993, but it covered only a proposed method for collecting DTI data at a voxel level, with no means of performing the voxel-by-voxel calculations in an image array, and no method for tractography. They could not create a recognizable first brain image, but only rotated a pork loin in an MRI scanner to show that the fibers would change intensity when the muscle tissue was reoriented.
The key difference in the two images—a set of two-dimensional gray patches versus a pyramidal tract tractogram—was due to a discovery by Filler and Howe, which they reported in 1992 but which Basser and Le Bihan and others failed to notice in the literature. Many researchers at the time knew that a tensor method needed to be developed. Both Filler and Basser were familiar with the tensor mathematics. However, none of the other scientists solved a difficult issue in MRI physics that was blocking the way forward.
There is an interference that arises, called a cross term, in which the magnetic field from a diffusion gradient shot in at an off angle disrupts the magnetic field from the location gradients that are along the x-, y-, and z -axes of the scanner, which are necessary for MR imaging. Multiple researchers at the time knew that this was the unsolved problem (see Moseley et al., Mori and van Zijl, Le Bihan et al., and Conturo et al. ). Indeed, Basser reported in his history that when he told Le Bihan they just needed to measure the diffusion signal in six different directions, he was crestfallen when Le Bihan said he knew this was necessary, but no one knew how to do it.
This was the problem that Filler and Howe solved in February 1992 32 —developing a process of refocusing the location gradients in order to virtually eliminate the destructive cross terms. Mori and van Zijl published a nearly identical strategy to reduce the interference in their 1995 paper, but this was not sufficient by itself to make DTI possible. As pointed out by the Filler group, with this solution set forth in detail in their patent, diffusion gradient application directed from an essentially infinite number of different directions is possible.
The physical basis of the DTI technique is that water tends to diffuse more rapidly along the long axis of an axon as opposed to diffusing transversely through the walls of the axon. At a theoretical level, water should be able to diffuse transversely through axon membranes and myelin sheaths, but the directionality of water diffusion in neural tissue is well proven. When water diffuses uniformly in all directions in a material or tissue, that pattern is described as isotropic, or equal in all directions. When there is a preferred direction of diffusion, then the behavior of water in that tissue is termed anisotropic.
Fundamentally, MRI scanning is based on measurement of nuclear spins of water protons. A proton in a given compound (such as the hydrogen proton in a water molecule) spins around its axis at a rate that is related to a surrounding magnetic field based on the Larmor equation. Stated simply, for example, if the applied magnetic field is at 4.7 T, the water protons will have an intrinsic spin rate of exactly 200 MHz (200 million times around per second). If radiofrequency (RF) energy is pumped into the volume of water in the 4.7-T field at a frequency of 200 MHz, then that will be introducing energy at exactly the resonant frequency of those protons, and they will commence absorbing the energy.
At the start, all of the protons can be thought of as standing vertically, each spinning on its axis and all aligned with the direction of the main magnetic field of the scanner. The absorbed energy cannot make the proton spin any faster; however, like a top, the proton’s magnetic axis may be pushed off of vertical so that the protons begin to precess, all coherently with one another, in response to the incoming wave of the applied RF signal. In MR, a pulse of RF is applied at the exact necessary frequency and then the RF is turned off and an antenna is brought into use to detect an RF signal coming back from the spinning protons as they coherently precess en masse, giving off their excess energy as the “spinning tops” return toward vertical. With elapsing time—a few microseconds—the excess energy will gradually be transmitted out of the coherently spinning protons, and the signal from the protons will decay away as their vertical axis of spin returns to alignment with the main magnetic field.
In T1 or T2 MR paradigms, the rate of decay provides the image contrast, with some tissues having faster or slower rates of decay. T1 decay relates to interactions between the spinning protons and magnetically active components in surrounding tissue components, whereas T2 contrast is related to decay interactions with other spinning protons.
The difference between nuclear magnetic resonance (NMR)—a laboratory technique going back to the 1950s—and MRI is the application of “locational” magnetic gradients that establish a three-dimensional Cartesian grid in MRI. A gradient is an addition to the main magnetic field such that, for instance, for voxels on the left side of the imaging volume the field strength is at 4.72 T and for voxels on the right side of the volume the field strength is at 4.68 T. The spin frequency for protons in the voxels on the left will be higher (e.g., 200.1 MHz), and the resonant frequency for protons in the voxels on the right side will be lower (e.g., 199.8 MHz).
The gradient is turned on briefly by running an electrical current through a loop of wire that results in generation of a magnetic field. The field is strongest near the loop and lowest at a distance, so there is a gradient from weak to strong along one direction. A first gradient is applied from head to foot (axial or z -axis—“slice select”), a second gradient is applied from back to front (anteroposterior or y -axis—“phase encode”), and a third gradient is applied right to left (transverse or x -gradient— “frequency encode”). When all three gradients are used, each voxel in the three-dimensional volume will have a unique and different field strength, so each will have a unique and distinct resonant frequency and phase. The system can learn about signal strength in each voxel and know exactly where in the three-dimensional grid each of the voxel signal return sources is located.
With this—the invention of MRI (by Paul Lauterbur and by Raymond Damadian )—it became possible to individually and separately address different voxels in an image. If one wanted to test a voxel in the lower left part of the volume in the back, one would use a lower precise frequency to stimulate and the antenna to learn the decay rate in that voxel, and so on. In this fashion the decay rate could be individually measured in each separate voxel in the imaged volume, such as the brain. Operationally, all the different frequencies are pumped in at the same time (often slice by slice).The receiving antenna receives a complex cacophony of thousands of signals at the full array of frequency and uses the mathematics of Fourier transforms to sort the data into an ordered array of data measurements. The measurements are repeated a number of times over—for example, a second—and some voxels will begin to decay in strength faster. For a T2 image, voxels with cerebrospinal fluid (CSF) will decay slowly and will still have a bright strong signal at the end of the second, whereas voxels with denser brain tissue will have return resonance signals that decay more rapidly and so can be shown as a darker voxel (three dimensional) or a darker pixel (two dimensional) on an image on the screen.
Diffusion MRI is based on the addition of an additional magnetic field gradient during the image acquisition. In this case the gradient is used to make a measurement of the diffusion of water. When the diffusion gradient is applied there will be (as for the imaging gradients), for example, a higher field strength on the left side of the voxel and a lower strength on the right side of the voxel. If water molecules with their protons diffuse (physically move or spread owing to brownian forces of energy such as heat) equally in all directions, then the diffusion is isotropic or equal in all directions.
At the initial instant of the imaging experiment, all the water molecules in the voxel are set to precessing coherently, all spinning at their resonant frequency for the applied field strength (e.g., 4.7 T, so 200 MHz). However, as some of the water molecules wander, by diffusion, into an area of the voxel where the applied diffusion gradient is stronger, they will speed up. Others will diffuse or spread into areas of the voxel where the applied main magnetic field is weaker and will slow down by a small amount. Very soon the various water protons in the voxel will each have their own distinct spin rate frequencies. The coherence of the signal will have decayed owing to their diffusion or physical movement in the voxel.
In a voxel with isotropic diffusion (e.g., CSF), this decay of the coherent signal due to diffusion movements will happen at exactly the same rate whether the diffusion gradient is applied from right to left or from head to toe, and so on. However, in axons, diffusion is anisotropic. Water molecules diffuse preferentially up and down the length of an axon. If, for instance, a peripheral nerve is to be imaged as to diffusion, we can consider what happens when a gradient is applied perpendicular to the nerve direction. The entire length of the nerve will travel along at one level of the gradient strength. The water diffusion preferentially up and down the length of the axon will not experience decay from diffusion, because as the molecules diffuse up and down along the axon, they remain at the same gradient strength. However, if the gradient is then turned so that it is applied down the length of the nerve—higher strength proximally, lower strength distally—then as the water diffuses the molecules will move rapidly into higher or lower magnetic field strengths at a rapid rate and there will be accelerated decay from diffusion.
In isotropic tissue, the gradual decay rate caused by the diffusion gradient is the same no matter which way the gradient is oriented. However, for an anisotropic tissue such as a nerve axon, the rate of diffusion decay is highly dependent on the orientation of the applied diffusion gradient. Because of this difference, a given voxel will remain brightest when the gradient is applied perpendicular to the long axis of an axon passing through it; will be intermediate in decay rate if it contains isotropic tissue; and will decay rapidly, becoming dark in intensity, if it contains an axon and the gradient is applied parallel to the direction of the axon. Because of this, we can learn about the direction in which an axon is oriented by the way its image signal strength responds to the orientation of a particular applied diffusion gradient.
Diffusion MRI was first introduced into clinical use because of its capability to detect stroke in an MRI scan. There is a characteristic pattern of image intensities in a brain MRI image slice when diffusion gradients are applied. However, in the setting of stroke, axons start to lose their apparent diffusion when they suffer infarction. Therefore the image characteristics of a diffusion-weighted MR image will start to change in an area affected by stroke. The affected area of neural tissue will begin to act as if it were restricted or decreased rather than unrestricted. For diffusion-weighted MRI, there is no need to know the precise direction of diffusion.
One additional technical aspect of diffusion MRI is that the diffusion gradient is pulsed on twice during each acquisition to actually detect the effect. In essence, it is turned on briefly to “label” the protons by giving them a particular coherent spin at their location at the beginning of the acquisition and then it is pulsed on a second time a few milliseconds later with the two pulses symmetrically placed on either side of the 180-degree inversion pulse. The difference in physical position in the gradient between the two pulses will sharply and precisely delineate the effects of diffusion. This is called a Stejskal-Tanner pulse after its two developers. ,
As described earlier, when the orientation of a nerve is simple and linear and known in advance (such as the median nerve in the upper arm), diffusion-weighted gradients can be applied parallel or perpendicular to the nerve to show the anisotropy, or health, of the nerve. However, as in many locations for peripheral nerves and for most locations in the brain, neural tracts will curve and turn as they progress, so there is no simple method of planning a perpendicular or parallel diffusion gradient. In DTI or in vector versions (e.g., HARDI, Q-Ball imaging), a larger number of gradient directions are applied and mathematical methods are then used to calculate neural direction on a voxel-by-voxel basis.
Note, however, that the diffusion gradients have to be set to about 10 times the strength of the location gradients in order to work. Without diffusion gradients, there is an ordered array of magnetic field strengths voxel by voxel in a cube generated by the x, y, and z gradients. With the addition of a far more powerful gradient from some off angle, the ordered array of field strengths set up by the location gradients, particularly the “phase encode” or y gradient, turns to chaos. These interactions are called cross terms, and they made it impossible to actually get a useful image when off-angle gradients were applied to generate tensor data.
For standard diffusion-weighted MRI, a single diffusion gradient could be applied parallel to one of the location gradients. The cross terms could be managed in this situation by using a balanced opposing pair of gradients—for example, one pointing along the x -axis and a second one pointing in the same orientation but from the opposite direction. However, to calculate a tensor, it was necessary to send in diffusion gradients from multiple different angles. As Mori pointed out, the two balanced pulses Neeman had proposed have to arrive at substantially different times, so diffusion is progressing between the two arrival times and therefore full correction is not possible. With the added the complexity of a gradient that is not parallel to the location gradient, the geometry of correction becomes inordinately complex. The cross terms get far more complicated. There is then the additional issue that multiple images, at least seven, will be obtained with different gradient orientations, so failures of compensation will be different from one gradient direction to the next, even as the water molecules are diffusing in complex, anatomically determined pathways that do not follow a Cartesian grid.
The fundamental invention that created the field of DTI—which is wholly attributable to the Filler group in their US patent number 5,560,360—was a method for allowing a non-Cartesian gradient (a gradient not directed along the x-, y-, or z -axis) to be applied without destroying the locational gradients ( x, y, and z ). Unlike in other scientific fields (such as the use of tensor analysis to determine the direction of magnetization in anisotropic rocks by the Harvard group where Filler trained [Tauxe and colleagues]) the same physical process (precisely oriented magnetic field gradients) is used to create the image in MRI and to apply the method for disruption to assess diffusion direction and anisotropy.
Filler identified the problem in 1991 and tasked Franklyn Howe, an MRI physicist, with finding a refocusing method that would work intrinsically with each gradient orientation (no balanced pair). Howe developed two different methods of refocusing the location gradients immediately after each application of a diffusion gradient so that diffusion could be measured in any direction without disrupting the image being created simultaneously by the image gradients. This discovery was published in 1992 showing detailed high-resolution imaging despite application of an off-angle diffusion gradient. With this problem solved, there was no limit to how many diffusion gradient directions could be obtained without the image being significantly affected by cross terms.
In addition, based on work by co-inventor Todd Richards, the group showed that the image could be constructed in an entirely novel way. In radiography, CT, MRI, and DWI, the result of imaging is that each voxel in the image is ultimately assigned a single image intensity number (a scalar quantity). These various shades of black, gray, and white make up the image, whether as exposed silver grains on a film or as pixel intensities on a computer monitor screen.
In the diffusion anisotropy techniques (e.g., DTI, HARDI, Q-Ball), each voxel becomes the subject of a mathematical calculation, with the result that it contains one or more vectors and not a single scalar quantity. The direction(s) of the vector will show the orientation of axons in the voxel, and the length of the vector will show the health or relative degree of anisotropy in that voxel. For simple DTI methods, each voxel can contain only one vector. For the vector methods HARDI and Q-Ball, for instance, there can be multiple vectors in the voxel, illustrating the fact that there may be crossing, joining, or splitting brain tracts captured within a single voxel. Richards et al. published this methodology for mathematically combining the several different diffusion direction image acquisitions into a single image whose voxels contained the directional information in 1992 as well.
For all of these diffusion anisotropy methods, the fundamental paradigm is to collect the image by using multiple diffusion gradients (each as a Stejskal-Tanner paired pulse , ). The gradients for a tensor method must be applied in a minimum of six different directions; modern DTI/DVI (diffusion vector imaging) scanning is typically done with about 30 directions of diffusion, but there may be as many as 256 directions of diffusion gradients applied for super-high resolution analysis. The MRI unit may still have the original design of just three gradient coils used for the three imaging gradients ( x, y, and z directions). However, by turning two or all three of them on together in multiple varying strengths, the scanner can generate an infinite number of diffusion gradient orientations. The gradient refocusing is carried out in the course of each gradient acquisition.
Prior to this advance, in papers such as the Moseley work on anisotropy, the researcher would publish a grid of four images, one routine with no diffusion, one showing how the slice appeared with an x -direction gradient, one with the y -direction appearance, and one with the z -direction appearance. Using Todd Richards’s method, it was possible to do a calculation for each voxel that incorporated all of the image results for that voxel and produced an invariant result. The data in the voxel would show the calculated orientation in space of an effective vector (either truly a vector or as the summary primary axis of a tensor). In addition, it would encode in the length of the vector—just how relatively isotropic or anisotropic the tissue was within that particular voxel.
The word tensor is involved for two entirely separate reasons. In physics the phenomenon of diffusion is called a tensor quantity. In anisotropic diffusion in various materials (rocks, polymer liquid crystal solutions, and so on) there is no single pure direction of movement, but rather the result is a sort of oriented ovoid or ellipsoid. It cannot be accurately and fully described by a single vector, but rather forms a sort of ovoid cloud of movement, with a long axis and two short axes. This is described as the tensor quantity phenomenon. One therefore can speak of the diffusion tensor as the quantity to be measured, although in clinical brain MRI we are interested in the orientation of axons and have no clinical interest in describing the niceties of “the diffusion tensor” of axonal tissue as a general physical phenomenon.
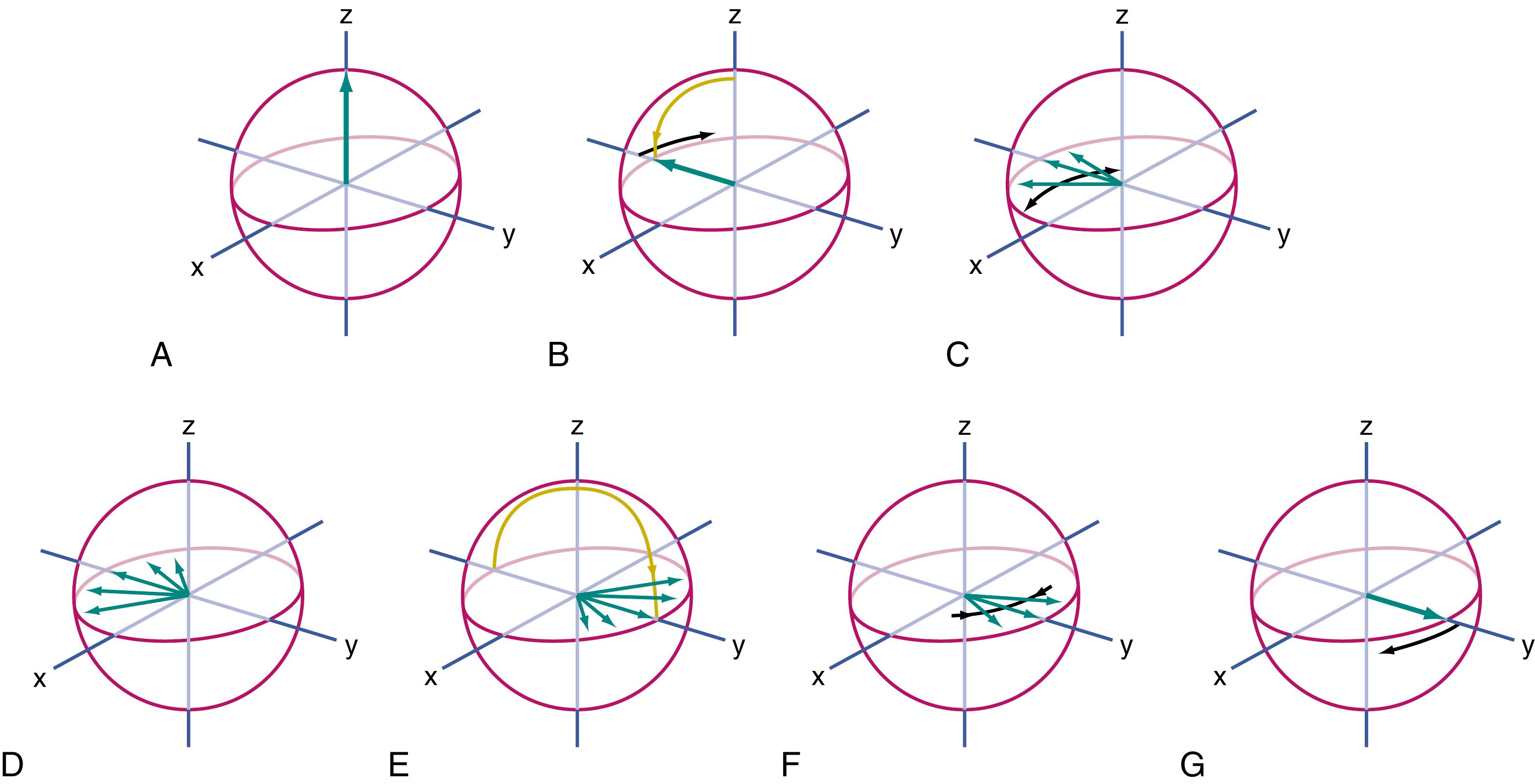
Separately, there is a type of mathematical analysis developed by Einstein called tensor analysis, , , which he applied to the study of space and time and also to the “Brownian motion” of diffusion. This mathematics is one of a number of mathematical techniques that can take an input of multiple vector measurements and convert them into a result that reveals the orientation and length of the principal axis of the ellipsoid and the orientation and length of the two short axes ( Fig. 14.5 ). This will show whether the ellipsoid is nearly spherical (as occurs in tissues with isotropic diffusion) or whether it is thin and elongated (as occurs in tissues with anisotropic diffusion), as well as determining the precise orientation in space of the principal or long axis of the ellipsoid. Typically in DTI of the brain, we are mostly interested in the long axis—its direction and how long is it (relative to the short axes). These are individually calculated for each voxel in the brain.
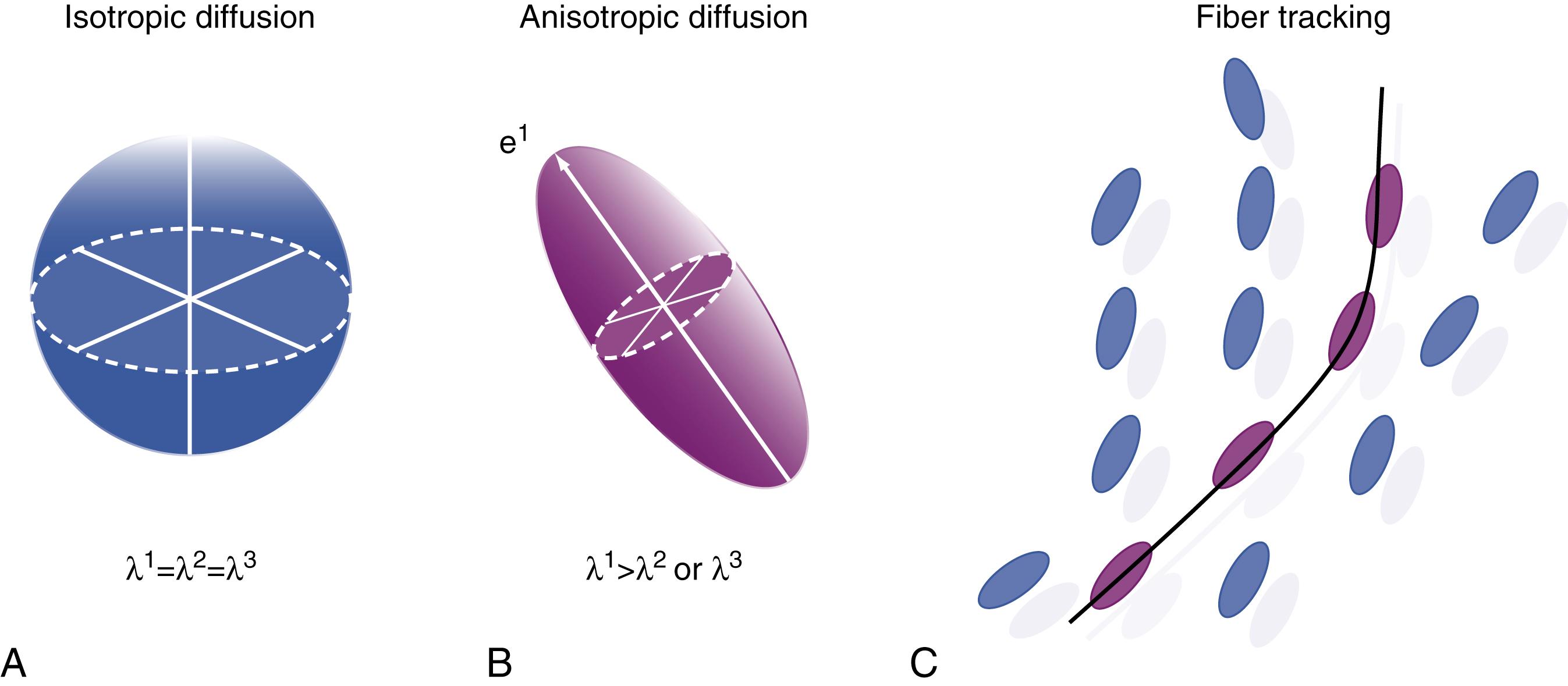
By contrast, in a vector mathematical analysis, multiple crossing, joining, or splitting tracts can be identified. A typical vector concept is based on treating each voxel as a multitessellated icosidodecahedron (polyhedron with 60 sides), like an elaborate buckminsterfullerene. We then simply ask if there are any faces of the polyhedron that are particularly bright on image acquisition. These will be potential multiple different axonal orientations within the single imaged voxel. There are also statistical spherical deconvolution methods ( Fig. 14.6 ) that can find multiple maxima for image directional intensity within the data space of each single vector. For certain regions of the brain, such as the optic radiation, the ability to follow multiple tracts and to follow tracts through sharp turns is critical for patient safety when tractograms are used to guide glioma surgery.
As a fourth aspect of the invention, Jay Tsuruda, a neuroradiologist, introduced the use of the connected voxel algorithm. This was a method under development at the time to improve carotid artery MR angiography. Tsuruda reprocessed brain image data produced by Richards to show that the algorithm could progress from voxel to voxel in a stepwise fashion. He also applied whole-volume ray projection (maximum intensity projection), but that method is not well suited to sorting out individual tracts. This led to the discovery that it was actually possible to produce images of brain tracts based on postprocessing of the voxel by voxel diffusion direction anisotropy data. The first DTI tractogram of the pyramidal tract appeared as Figure 17 in US patent number 5,560,360 (see Fig. 14.4 ).
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here