Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Pharmacokinetics describes the absorption, distribution, metabolism, and excretion of drugs. The pharmacokinetic parameters of a drug are used to characterize the drug concentrations reached within the body after a dose and the changes in those concentrations over time. Clinical pharmacokinetics is the discipline that applies pharmacokinetic principles to individualize dosage regimens, optimize the therapeutic effects of a medication, and minimize the chances of an adverse drug reaction. This is accomplished by achieving an effective concentration of unbound drug at the site of action. Clinically important sites of action include receptors, membrane transport systems, intracellular enzymes, interstitial tissues where infections may occur, and many others. Correlations have been made between drug concentrations in the circulation and effective or toxic drug concentrations at various sites of action. Depending upon the strength of those correlations, ranges of effective, toxic, and ineffective circulating drug concentrations have been defined for many drugs. Pharmacokinetics serves as a guide to effective therapy, but achieving specific concentrations is not the goal of therapy. Effective therapy is best judged by improvements in function, not just by reaching the desired peak and trough concentrations in the circulation.
The physiologic processes that transform drugs and remove them from the body were characterized decades ago using simple exponential equations. More modern mathematical approaches provide greater insight into both the rates of these processes and the influence of diverse patient factors upon these rates using nonlinear mixed effects modeling (NONMEM). NONMEM is often combined with the sparse sampling techniques of population-based pharmacokinetics that are critical for measurement of pharmacokinetics in extremely low-birth-weight newborns with limited blood volumes and challenging vascular access. The results of NONMEM analyses can then be used in Monte Carlo simulations to predict the range of concentrations expected from particular dosages in specific patient populations.
The basic physiologic processes involved in pharmacokinetics remain relevant to understanding how to produce optimal concentrations of drugs at the site of action and how to adjust dosages in clinical practice. The change in drug amount within the body can be described by the following general equation in which A is the amount of drug within the body, k is the rate constant of change for A within the body, and n defines the order (e.g., zero, first, second) of the process.
The simplest description begins with the intravenous infusion of a single dose. Infusions are usually carried out with a syringe pump that provides a constant rate of flow (mg/min). Constant rates are described by zero-order exponential equations in which e 0 = 1.
After a drug enters the circulation composed of red blood cells, proteins, and serum (the water and electrolyte solution), it may remain in that space in the water layer or bind to one of the components of blood, such as albumin, α 1 glycoprotein, or red blood cells, or it may be transported or diffuse across the endothelial membrane out of the circulation. This binding within the circulation is important because only the unbound portion of a drug is free to diffuse across membranes to reach sites of action, sites of metabolism (such as in the hepatocyte), or sites of excretion (such as the renal tubule). Preterm newborns often have reduced total proteins in their circulation, causing a greater percentage of the circulating drug concentration to remain unbound. This can lead to drug toxicity at total circulating concentrations regarded as nontoxic and therapeutic based on studies in adults or older children with higher protein concentrations.
Most drugs are eliminated by first-order exponential rates (k) in which a constant fraction of the drug is eliminated per unit of time. If the kinetics are determined by first-order elimination, then the rate of change of drug in the body (d A /d t ) is proportional to the amount in the body. Thus at high concentrations a greater amount of drug is eliminated per hour than at low concentrations. For example, if the concentration is 100, it will decrease to 50 in one half-life, a loss of 50, but during the next half-life, only 25 will be removed as the concentration decreases from 50 to 25. This exponential decline in plasma concentration ( Fig. 16.1 ) can be represented by the following equation:
where C t is the concentration at some time t , C 0 is the initial concentration at time 0, and e −kt represents the exponential decline in plasma concentration associated with first-order elimination. The exponential decrease in plasma concentration with time may be made linear by taking the natural logarithm of each side of Eq. (16.3) to convert this to the equation for a straight line, y = mx + b .
The slope of this straight line is the elimination rate constant k (time −1 ), which may be calculated by rearranging Eq. (16.4) :
where C 1 is the higher early concentration and C 2 is the lower concentration measured some time later. If the logarithm (base 10) of concentration is graphed versus time, the slope will be k /2.303. The relationship between the elimination rate constant and the half-life for a first-order process may be derived mathematically from Eq. (16.3) . For a drug whose initial concentration is 100 mg/L, the concentration at one half-life is 50 mg/L.
which can be rearranged to
where t represents one half-life; because Ln2 = 0.693, the equation becomes
When circulating concentrations are sampled quickly after intravascular drug infusion, the concentration can be used to estimate the distribution volume within the central compartment defined as the volume necessary to describe the change in concentration produced by a specific dose:
This volume can be viewed as the volume required to dilute the concentrated dosage formulation to the concentration of drug observed within the body.
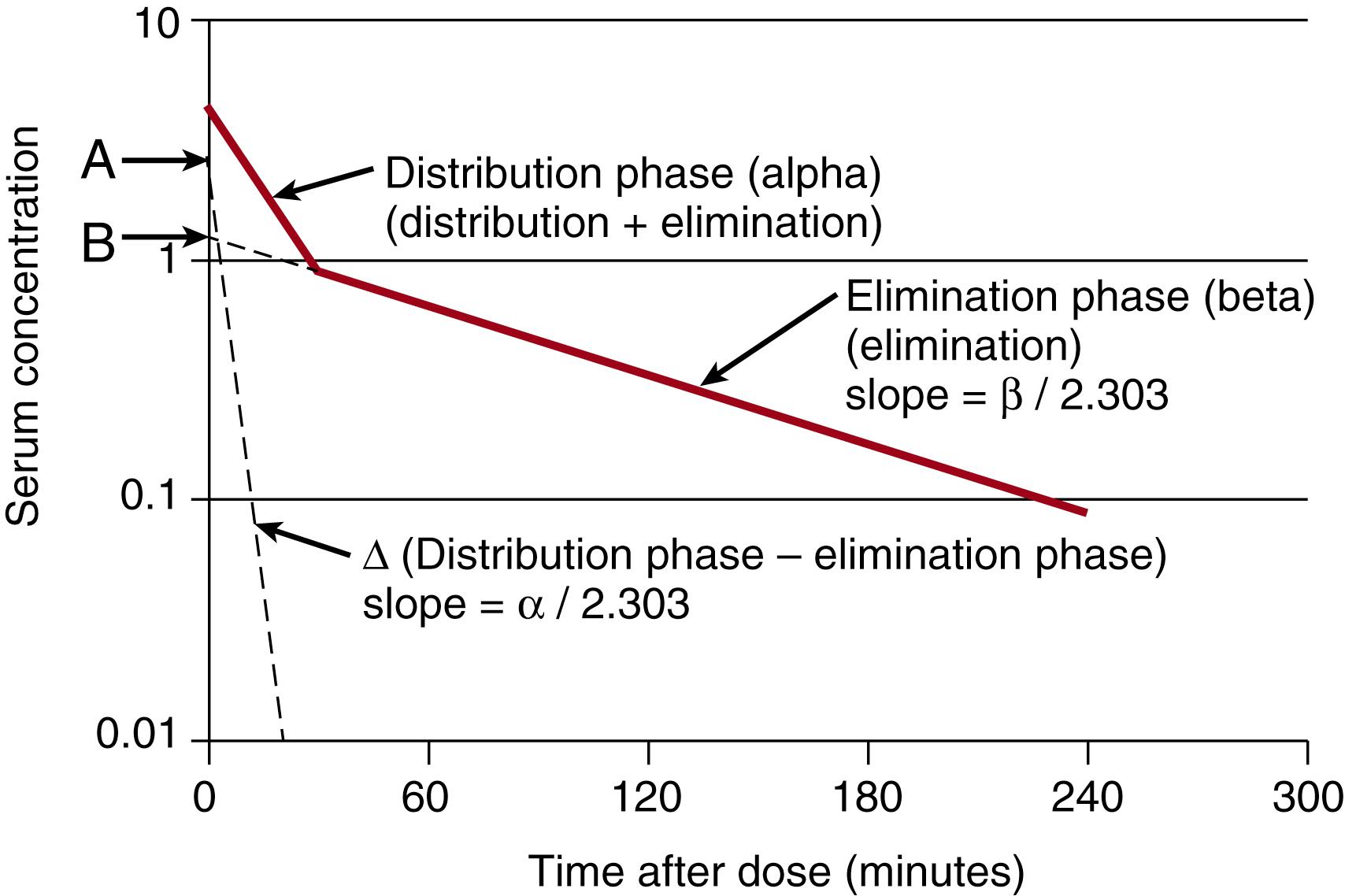
For drugs that begin to diffuse out of the circulation soon after administration, the initial drop in concentration due primarily to diffusion is termed the distribution phase . It is generally followed by a phase with a slower decrease in concentration, reflecting elimination by excretion of unchanged drug or by metabolism of the parent molecule that was administered. This produces the familiar biphasic concentration-time graph (see Fig. 16.1 ) that can usually be fitted to two or occasionally three first-order exponential terms (concentration = Ae − α t + Be −β t ).
The multipliers of time (t) , α and β, provide the rate constants for the different rates of drug removal. These rate constants with units of time -1 are inversely related to the half-life by the natural logarithm of 2. The rate of distribution is defined by the following equation:
Accurate analysis of these rate constants using the older techniques of pharmacokinetics is complicated because both distribution and elimination are occurring simultaneously after the drug enters the circulation. To determine the rate of the distribution phase requires subtracting the change in concentration due to the slower β (elimination) phase (see Fig. 16.1 ). This procedure is referred to as curve stripping .
When there is a third phase after the α and β phases, it is usually attributed to distribution into and out of deep tissue compartments, such as fat or bone, during this third, or γ, phase. In reality these are artificial explanations that may or may not explain the actual movement of the drug within the body, but they do describe the observed changes in concentration. More important, these basic mathematical approaches do not account for factors that may contribute to significant changes in concentration that are especially relevant to neonatal studies. These include factors such as gestational age, urine output, organ dysfunction, and interactions with other drugs. The influence of these factors can be determined using NONMEM, described later in this chapter.
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here