Radiation Detection & Ancillary Instrumentation

Radiation detection

Consider the model of a basic radiation detector, as shown in Fig. 2.1 . The detector acts as a transducer that converts radiation energy to electronic charge. Applying a voltage across the detector yields a measurable electronic current. Radiation detectors typically operate in either of two modes, current mode or pulse mode. Detectors that operate in current mode measure the average current generated within the detector over some characteristic integration time. This average current is typically proportional to the exposure rate to which the detector is subjected or the amount of radioactivity within the range of the detector. In pulse mode, each individual detection is processed with respect to the peak current (or pulse height) for that event. This pulse height is proportional to the energy deposited in the detection event. The histogram of pulse heights is referred to as the pulse-height spectrum. It is also referred to as the energy spectrum because it plots a histogram of the energy deposited within the detector.

Certain properties of radiation detectors characterize their operation. Some are applicable to all detectors, whereas others are used for detectors that operate in pulse mode. These characterizations are not only useful for describing the operation but can also give insight into the benefits and limitations of the particular detector.

The detection efficiency depends on several factors, including the intrinsic and extrinsic efficiency of the detector. The intrinsic efficiency is defined as the fraction of the incident radiation particles that interact with the detector. It depends on the type and energy of the radiation and the material and thickness of the detector. For photons, the intrinsic efficiency, D _I , is given to first order by:

where μ is the linear attenuation coefficient for the material of interest at the incident photon energy, and x is the thickness of the detector. Thus the intrinsic efficiency can be improved by using a thicker detector or choosing a photon energy and detector material that optimizes the value of μ.

The extrinsic efficiency is the fraction of photons or particles emitted from the source that strike the detector. It depends on the size and shape of the detector and the distance of the source from the detector. If the detector is a considerable distance from the source (i.e., a distance that is >5 times the size of the detector), the extrinsic efficiency, D _E , is given by:

where A is the area of the detector, and d is the distance from the source to the detector. This equation defines the inverse square law. For example, if the source-to-detector distance is doubled, the intensity of the radiation beam is reduced by a factor of 4. The total detection efficiency is the product of the intrinsic and extrinsic efficiencies:

In pulse mode, the pulse height is proportional to the energy deposited within the detector. However, the uncertainty in the energy estimation, referred to as the energy resolution, depends on the type of detector used and the energy of the incident radiation. For a photon radiation source of a particular energy, the feature associated with that energy is referred to as the photopeak, as shown in Fig. 2.2 . The width of the photopeak, as characterized by the full width at half of its maximum (FWHM) value normalized by the photon energy represented as a percentage, is used as a measure of the energy resolution of the detector.

When the detector is subjected to a radiation beam of low intensity, the count rate is proportional to the beam intensity. However, the amount of time it takes for the detector to process an event limits the maximum possible count rate. Two models describe the count rate limitations: nonparalyzable and paralyzable. In the nonparalyzable model, each event takes a certain amount of time to process, referred to as the dead time, which defines the maximum count rate at which the detector will saturate. For example, if the dead time is 4 μs, the count rate will saturate at 250,000 counts per second. With the paralyzable model, the detector count rate not only saturates but can “paralyze”—that is, lose counts at very high count rates. Gamma cameras, for example, are paralyzable systems.

The three basic types of radiation detectors used in nuclear medicine are gas detectors, scintillators, and semiconductors. These three operate on different principles and are typically used for different purposes.

Gas detectors are used every day in nuclear medicine for assaying the amount of radiopharmaceutical to be administered and to survey packages and work areas for contamination. However, because of the low density of gas detectors, even when the gas is under pressure, the sensitivity of gas detectors is not high enough to be used for clinical counting and imaging applications.

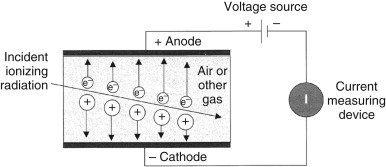
A gas radiation detector is filled with a volume of gas that acts as the sensitive material of the detector. In some cases it is air, and in others it is an inert gas such as argon or xenon, depending on the particular detector. Electrodes are located at either end of the sensitive volume. The detector circuit also contains a variable voltage supply and a current detector. As radiation passes through the sensitive volume, it causes ionization in the gas. If a voltage is applied across the volume, the resulting ions (electrons and positive ions) will start to drift, causing a measurable current in the circuit. The current will last until all of the charge that was liberated in the event is collected at the electrodes. The resulting current entity is referred to as a pulse and is associated with a particular detection event. If only the average current is measured, this device operates in current mode. If the individual events are analyzed, the device is operating in pulse mode.

Fig. 2.3 shows the relationship between the charge collected in the gas detector and the voltage applied across the gas volume. With no voltage, no electric field exists within the volume to cause the ions liberated in a detection event to drift, and thus no current is present and no charge is collected. As the voltage is increased, the ions start to drift, and a current results. However, the electric field may not be sufficient to keep the electrons and positive ions from recombining, and thus not all of the originally liberated ions are collected. This portion of Fig. 2.3 is referred to as the recombination region. As voltage is increased, the level is reached at which the strength of the electric field is sufficient for the collection of all of the liberated ions (no recombination). This level is referred to as the saturation voltage, and the resulting plateau in Fig. 2.3 is the ionization chamber region. When operating in this region, the amount of charge collected is proportional to the amount of ionization caused in the detector and thereby to the energy deposited within the detector. Ionization detectors or chambers typically operate in current mode and are the detectors of choice for determining the radiation beam intensity level at a particular location. They can directly measure this intensity level in either exposure in roentgens (R) or air kerma in rad. Dose calibrators and the ionization meters used to monitor the output of an x-ray device or the exposure level from a patient who has received a radiopharmaceutical are examples of ionization (or ion ) chambers used in nuclear medicine.

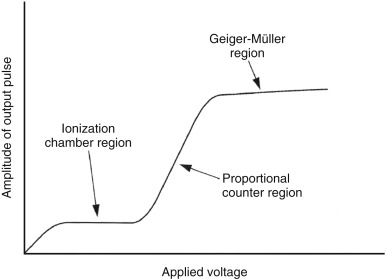
If the voltage is increased further, the drifting electrons within the device can attain sufficient energy to cause further ionizations, leading to a cascade event. This can cause substantially more ionization than with an ionization chamber. The total ionization is proportional to the amount of ionization initially liberated; therefore these devices are referred to as proportional counters or chambers. Proportional counters, which usually operate in pulse mode, are not typically used in nuclear medicine. If the voltage is increased further, the drifting electrons attain the ability to cause a level of excitations and ionizations within the gas. The excitations can lead to the emission of ultraviolet radiation, which also can generate ionizations and further excitations. This leads to a terminal event in which the level of ionization starts to shield the initial event, and the level of ionization finally stops. This is referred to as the Geiger-Müller process. In the Geiger-Müller device, every event leads to the same magnitude of response, irrespective of the energy or the type of incident radiation. Thus the Geiger-Müller meter does not directly measure exposure, although it can be calibrated in a selected energy range to milliroentgens per hour (mR/hr). However, the estimate of exposure rate in other energy ranges may not be accurate. The Geiger-Müller survey meter is excellent at detecting small levels of radioactive contamination and thus is often used to survey radiopharmaceutical packages that are delivered and work areas within the nuclear medicine clinic at the end of the day.

Scintillation detectors

Some crystalline materials emit a large number of light photons upon the absorption of ionizing radiation. This process is referred to as scintillation, and these materials are referred to as scintillators. As radiation interacts within the scintillator, a large number of excitations and ionizations occur. On de-excitation, the number of light photons emitted is directly proportional to the amount of energy deposited within the scintillator. In some cases, a small impurity may be added to the crystal to enhance the emission of light and minimize the absorption of light within the crystal. Several essential properties of scintillating materials can be characterized, including density, effective Z number (number of atomic protons per atom), amount of light emitted per unit energy, and response time. The density and effective Z number are determining factors in the detection efficiency because they affect the linear attenuation coefficient of the scintillation material. The amount of emitted light affects both energy and, in the gamma camera, spatial resolution. Resolution is determined by the statistical variation of the collected light photons, which depends on the number of emitted photons. Finally, the response time affects the temporal resolution of the scintillator. The most common scintillation crystalline material used in nuclear medicine is thallium-doped sodium iodide (NaI) with lutetium oxyorthsilicate (LSO) or lutetium yttrium oxyorthosilicate (LYSO) most commonly used in positron emission tomography (PET).

Once the light is emitted in a scintillation detector, it must be collected and converted to an electrical signal. The most commonly used device for this purpose is the photomultiplier tube (PMT). Light photons from the scintillator enter through the photomultiplier entrance window and strike the photocathode, a certain fraction of which (approximately 20%) will lead to the emission of photoelectrons moving toward the first dynode. For each electron reaching the first dynode, approximately a million electrons will eventually reach the anode of the photomultiplier tube. Thus the photomultiplier tube provides high gain and low noise amplification at a reasonable cost. Other solid-state light-detection approaches are now being introduced into nuclear medicine devices. In avalanche photodiodes (APDs), the impinging light photons lead to the liberation of electrons that are then drifted in the photodiode, yielding an electron avalanche. The gain of the APD is not as high as with the PMT (several hundred compared with about a million), but the detection efficiency is substantially higher (approximately 80%). A second solid-state approach is the silicon photomultiplier tube ( SiPMT ). This device consists of hundreds of very small APD channels that operate like small Geiger-Müller detectors—that is, each detection is a terminal event. The signal from the SiPMT is the number of channels that respond to a particular detection event in the scintillator. SiPMTs have moderate detection efficiency (approximately 50%) and operate at low voltages. One further advantage of APDs and SiPMTs compared with PMTs is that they can operate within a magnetic field. Thus the development of positron emission tomography/magnetic resonance (PET/MR) scanners has involved the use of either APDs or SiPMTs.

Solid-state technology is used to detect the light from a scintillation detector and also can be used to directly detect gamma rays. The detection of radiation within a semiconductor detector leads to a large number of electrons liberated, resulting in high energy resolution. The energy resolution of the lithium-drifted germanium (GeLi) semiconductor detector has approximately 1% energy resolution compared with the 10% energy resolution associated with a sodium iodide scintillation detector. However, thermal energy can lead to a measurable current in some semiconductor detectors such as GeLi, even in the absence of radiation, and thus these semiconductor detectors must be operated at cryogenic temperatures. On the other hand, semiconductor detectors such as cadmium telluride (CdTe) or cadmium zinc telluride (CZT) can operate at room temperature. CdTe and CZT do not have the excellent energy resolution of GeLi, but at approximately 5%, it is still significantly better than that of sodium iodide.

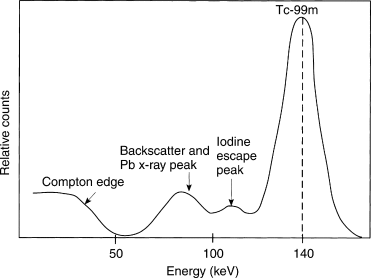
The pulse height spectrum corresponding to the detection of the 140-keV gamma rays from technetium-99m (Tc-99m) is illustrated in Fig. 2.4 . The photopeak corresponds to events where the entire energy of the incident photon is absorbed within the detector. These are the events of primary interest in most counting experiments, and thus the good events are within an energy acceptance window about the photopeak. Other events correspond to photons scattered within the detector material and depositing energy, which can range from very low energy from a very-small-angle scatter to a maximum 180-degree scatter (in the spectrum referred to as the Compton edge ). Events below the Compton edge correspond to these scattered events. In some cases, photons can undergo multiple scatters and possibly result in events between the Compton edge and the photopeak. Photons scattered within the patient and then detected may also result in events in this energy region. Finally, the pulse-height spectrum will be blurred depending on the energy resolution of the detector. Thus in Fig. 2.4 , the photopeak has approximately a 10% spread because of the energy resolution associated with NaI, rather than the narrow spike that might be expected from the emission of a monoenergetic gamma ray.