Theory of Rotors and Arrhythmias

Arrhythmogenesis in a Ring of Tissue

The idea of rotational activity in application to cardiac arrhythmias has been around for more than a century, when it was described as follows: “If a closed circuit of muscle of considerably greater length than the wave of excitation is provided, it is possible to start a wave in this circuit which will continue to propagate itself round and round the circuit for an indefinite number of times.” In modern terms, two important properties of cardiac tissue need to be considered: the ability to conduct pulses of excitation with velocity (v) and the existence of a refractory period (R), during which the tissue cannot be excited but recovers after it. As a result, if a wave is initiated propagating along a circle of cardiac tissue of length L, then the wave will make a complete rotation during time T = L/v. Then, as stated by Mines, if “a closed circuit length” L “greater than the wave of excitation” (Rv), that is, if L > Rv, the rotation along the circle will be sustained ( Fig. 33.1A ).

Rotor Formation

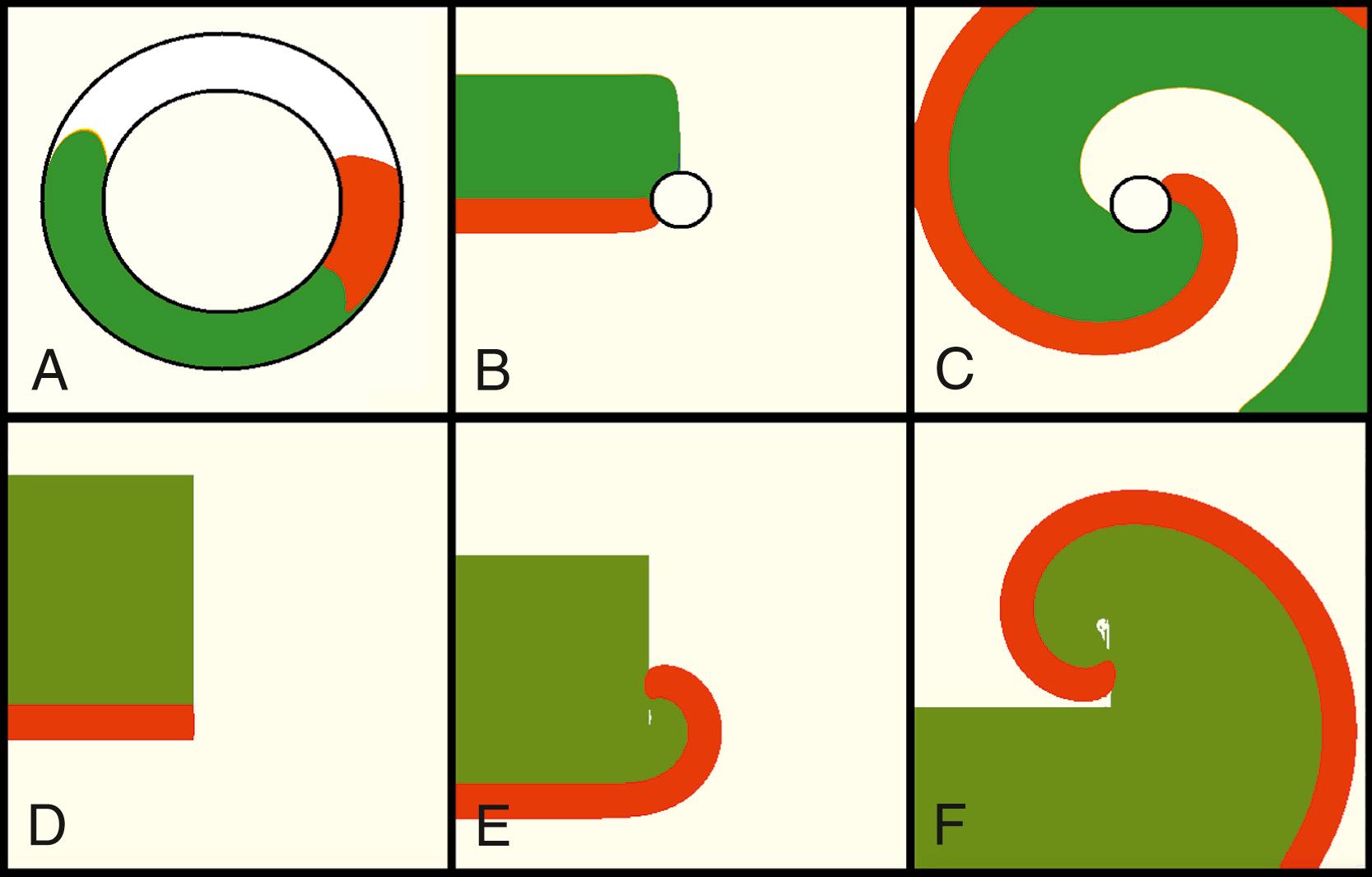
When a wavefront that propagates in a two-dimensional (2D) sheet of cardiac cells encounters an obstacle in its path, it will keep its endpoint on the obstacle over time and evolve into a spiral wave (see Fig. 33.1B–C ). The period of wave rotation around the obstacle (T) can again be estimated from the circumference of the obstacle (L) and the velocity of propagation (v) as T = L/v.

An important finding for 2D tissue was the understanding that such a rotation is also possible in tissue without any obstacles. In this case the excitation from a wave break (see Fig. 33.1D ) will propagate along the refractory tail of the wave until the end of the refractory period (see Fig. 33.1E ), then it will make a half-turn, continuously following the refractory tail (see Fig. 33.1F ).

In this situation, the wave rotates chasing its own refractory tail, which serves as a functional obstacle for wave propagation. Such rotating waves are often called rotors. An essential difference between rotors and spiral waves rotating around obstacles (anatomic reentry) is that the rotation period of a rotor is close to the refractory period of the tissue. This property can be understood from Fig. 33.1F , where the wavefront closely follows the refractory tail of the wave. Therefore rotors are believed to be responsible for the most dangerous arrhythmias (i.e., various types of tachycardia and fibrillation where the heart rate is exceedingly high).

If rotation around an anatomic obstacle is compared with a rotor, these sources show different dynamics. Anatomic reentry is normally a stationary periodic process that produces periodic electrocardiogram (ECG) characteristic of monomorphic arrhythmias. This happens because the tip of the wave follows the same route around the obstacle. Although rotors can also be stationary, for cardiac tissue it is rather exceptional. Theoretical studies revealed that, even in the absence of any heterogeneity, the rotation of the tip of the rotor can occur along a complex trajectory because of its interaction with the refractory tail of the wave. This process, called meandering, was first described by Zykov in low-dimensional models of excitable media, where meandering patterns can exhibit epicycloidal rotation (inward petals) or hypocycloidal rotation (outward petals) with few intermediate regimens. These types of dynamics turned out to be very general, and further research confirmed such meandering in many detailed models of cardiac tissue. Other types of rotor dynamics are discussed further later.

Rotors do not uniquely exist in the heart; they were first found in the Belousov-Zhabotinsky chemical reaction and many other physical and biologic systems. The Jalife group has extensively studied properties of rotors in cardiac tissue and their relation to cardiac arrhythmias using a range of experimental setups, from simple 2D preparations to the whole heart level. The importance of rotors for cardiac arrhythmias is widely recognized and can be found in most medical textbooks on cardiology. ^,

New Effects in Two Spatial Dimensions: Curvature and Anisotropy

Cardiac propagation is a result of excitation of the individual cardiac myocytes, and excitation is caused by local depolarization of myocytes. During its excitation, a myocyte generates a current that depolarizes the adjacent myocytes, which in turn become excited, thus continuing this process. When going from 1D to 2D wave propagation, additional factors affect the wave dynamics: wavefront curvature and anisotropy.

It was found that in two or three spatial dimensions, a positively curved wavefront (e.g., a wave initiated at an electrode) will propagate at a lower velocity than a planar wavefront ( Fig. 33.2 ). This fact is commonly explained as follows. In an expanding front, a smaller number of depolarized cells should provide current to depolarize a larger number of cells just ahead, which slows down the propagation velocity. The degree of current divergence is larger for a wavefront of smaller radius, and theoretical estimates showed that if the wavefront has a curvature higher than some critical value, it cannot expand and should collapse. In practice, it is also seen that a stimulating electrode with a too-small radius cannot be used to stimulate the tissue.

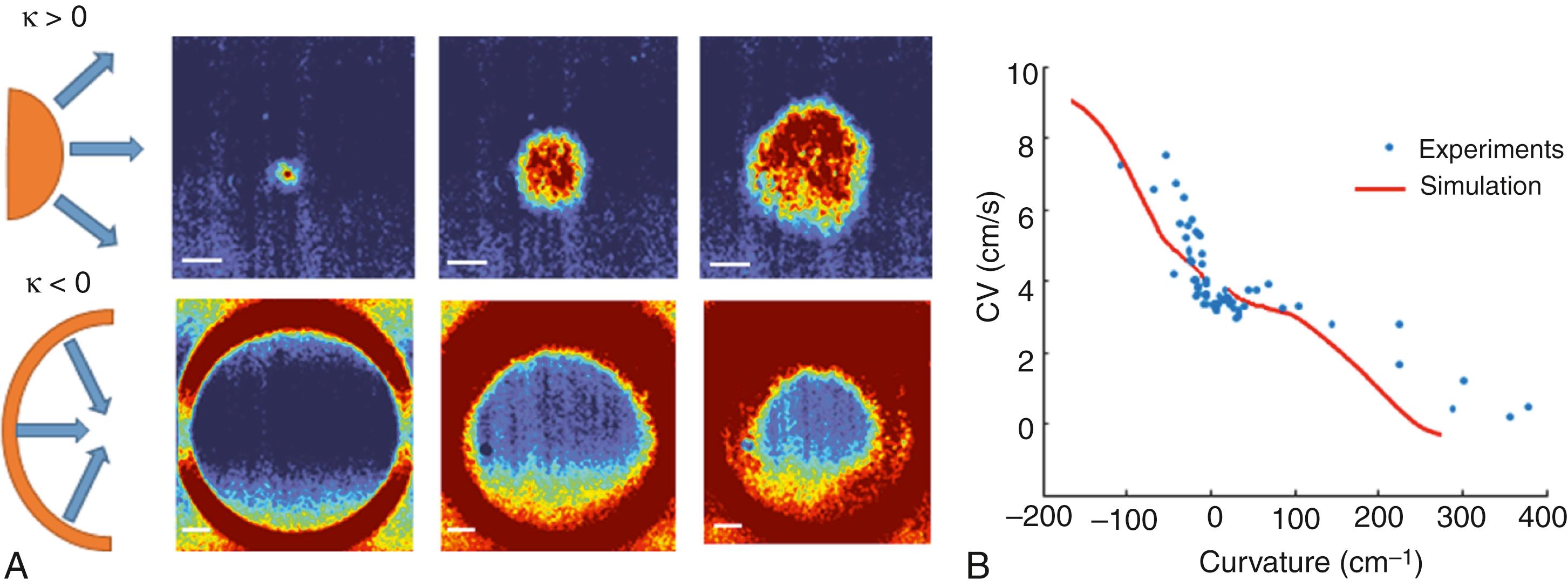
The effects of curvature on wave propagation velocity were reproduced in many theoretical studies and have been indirectly demonstrated in elegant experiments. ^, However, until recently, it was difficult to measure it in experiment. Today, the use of new methodologies and especially optogenetics allows researchers to perform more detailed studies of these phenomena. Using this methodology, it is possible to depolarize by light areas on any desired shape and study wave propagation originating from such areas. McNamara and coworkers quantified the effect of wavefront curvature on conduction velocity in monolayers of otopatch spiking human embryonic kidney (HEK) cells expressing sodium and potassium channels in parallel with numerical simulation of this process. They initiated expanding fronts with positive curvature (see top row of Fig. 33.2A ) and incoming waves with negative curvature. The effects of curvature on the velocity of wave propagation are shown in Fig. 33.2B together with simulations. Incoming waves have a higher velocity and expanding waves have a lower velocity than a planar front (i.e., front with zero curvature). The authors also estimated that the radius of critical curvature of the wavefront in their system was 25 mm. This is lower than the estimated 100 to 50 mm obtained using optogenetics in mouse ventricles and earlier estimates 200 to 100 mm obtained using circular electrodes.

However, experiments also reveal some paradoxical effects of curvature. Teplenin and colleagues studied excitations elucidated by depolarized areas of various shapes. It was paradoxically found that excitation can be more easily initiated by the areas of high curvature than by the areas of low curvature. Fig. 33.3 shows excitations initiated by depolarization in a “Pac-Man” shape. In the experiment ( Fig. 33.3 , top row) and in modeling studies ( Fig. 33.3 , bottom row) the excitation occurs at the highest curvature region of the Pac-Man shape. This is a paradoxical observation, as the density of current generated by the depolarized region is lowest at the region with highest positive curvature. In this case generation of new waves is a more complex process, which is a result of boundary instability of the whole system, and higher curvature here potentiates this bifurcation. Because the local generation of waves is linked to the formation of ectopic activity in the heart, this result shows that the onset of ectopic activity may depend on the shape of the abnormal region in a complex and nonintuitive way.

Another factor that strongly affects wave propagation in two and three spatial dimensions is the anisotropy of cardiac tissue. The myocardial wall is essentially a muscle consisting of myofibers. The myofibers are locally aligned, but their orientation changes in a rather complex manner throughout the heart, as myofibers gradually turn over 90 to 150 degrees through the myocardial wall. This anatomic fact is important for wave propagation because the waves of electrical depolarization travel two to three times faster along the myofiber direction than in the transverse directions. If wave propagation is observed in a local patch with well-aligned myofibers, anisotropy can be viewed as a mere rescaling of coordinate axes with the local conduction velocity; one of the recent developments in this area is that for more complex cases, one can study effects of anisotropy using rescaling via a curved space formalism from mathematical physics, which is discussed later.

Rotor Drift and Anchoring

Sources of Rotor Drift

Theoretical studies have shown that any type of inhomogeneity normally causes drift of the rotors. For example, a gradient of action potential duration (APD) induces a drift of rotors. Multiple numerical studies showed that the longitudinal component is always directed toward the region of the longer period of rotor rotation. The mechanism of this phenomenon is still unknown. For cardiac arrhythmias, this means that because of drift the cycle length of an arrhythmia will increase, which should present some antiarrhythmic effect. Because even in normal ventricles there are substantial differences in APD between the basal and apical regions, between left and right ventricles, and across the myocardial wall, such heterogeneity can directly affect the rotor dynamics during cardiac arrhythmia.

The change of muscle fiber direction (anisotropy) in the heart was also shown to produce drift of the rotors. Also, both heterogeneity and anisotropy can cause new rotors to form. The fact that heterogeneity in the refractory period can induce new rotors was established in classic works of Moe and colleagues and Krinsky. The fact that abrupt change in fiber orientation can induce blocks of wave propagation and formation of new rotors was established more recently in modeling and experimental studies. Interestingly, in a mathematical sense, a locally varying anisotropy can be viewed as change in the geometry of the wavefront. Thus the formation of waveblocks by anisotropy is like the effects of critical curvature discussed earlier.

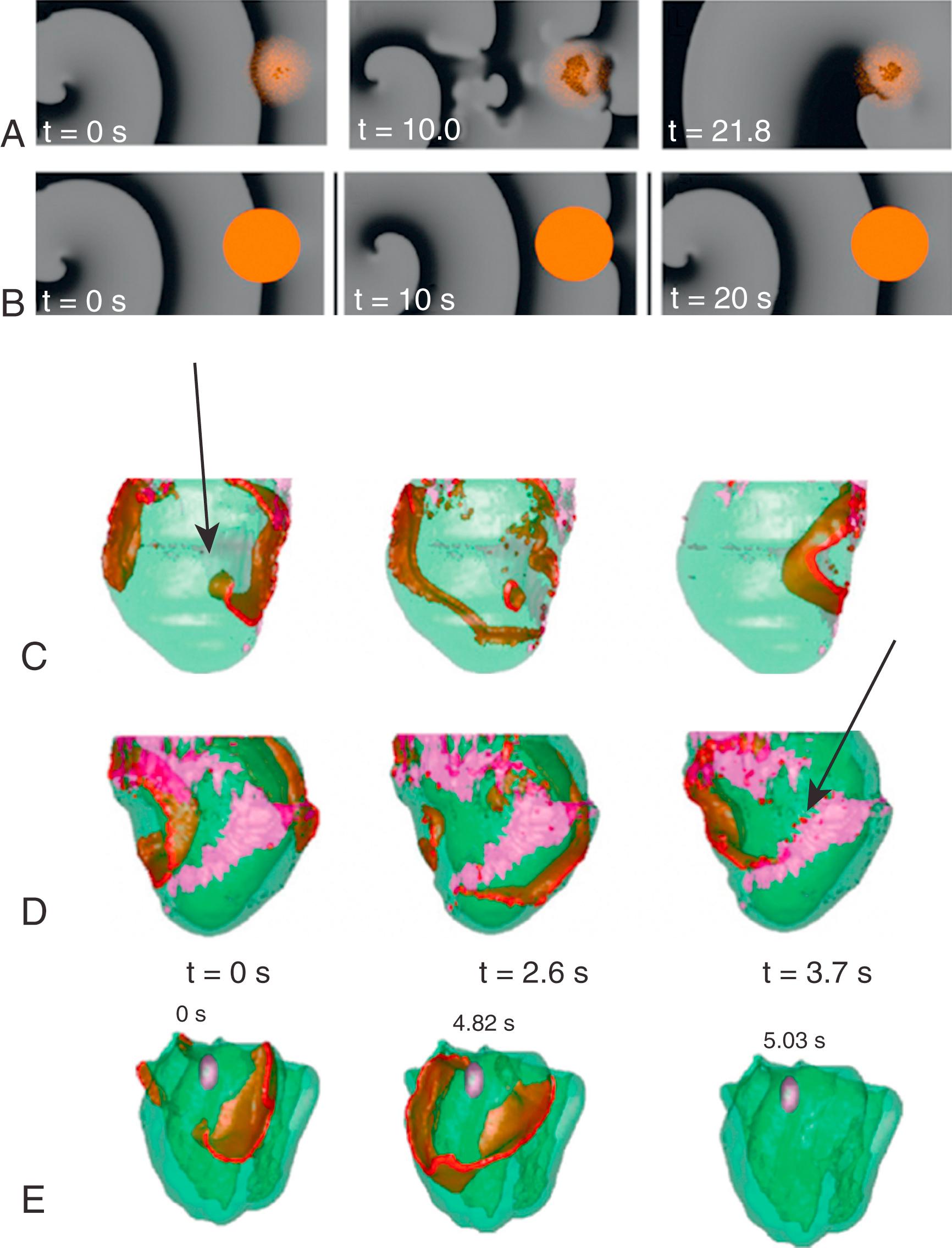
Because cardiac tissue has all types of heterogeneity, the first detailed recordings of rotors in an experiment showed that they drift. However, that study also described an extremely important process that was later called anchoring. During its drift, the rotor attached to the anatomic inhomogeneity and started to rotate stationary around it ( Fig. 33.4A ). Thus a transition from rotor to anatomic reentry was observed. Currently anchoring is considered one of the main factors that can stabilize arrhythmia in the heart and underlies many important clinical phenomena (e.g., it can explain the transition from polymorphic to monomorphic arrhythmias).