Principles of ultrasound

Key points

Ultrasound is mechanical energy in the form of vibrations that propagate through a medium such as tissue.
Ultrasound interacts with tissue by undergoing absorption, reflection, refraction, and scattering and produces an image representative of tissue structure.
Imaging artifacts can be recognized and understood based on a knowledge of the principles of ultrasound.

Basic ultrasound physics

Sound is a mechanical energy in the form of vibrations that propagate through a medium such as air, water, or tissue. The frequency of audible sound ranges from 20 to 20,000 Hz (cycles per second). Ultrasound involves a frequency spectrum that is greater than 20,000 Hz. Medical applications use frequencies in the range of 1,000,000 to 50,000,000 Hz (1 to 50 MHz). The propagation of ultrasound results from the displacement and oscillation of molecules from their average position and the subsequent displacement and oscillations of molecules along the direction of propagation of the ultrasound wave.

Ultrasound waves can be described using the common properties of waves. Fig. 1.1 is an illustration of a sinusoidal wave with the pressure amplitude along the y -axis and the time or distance along the x -axis. Fig. 1.1 is referred to in the following sections to introduce the basic properties of waves.

• Fig. 1.1, Sinusoidal wave depicted on the time axis and distance axis. The time to complete one cycle is the period (τ). The distance to complete one cycle is the wavelength (λ).

Wavelength, frequency, and velocity

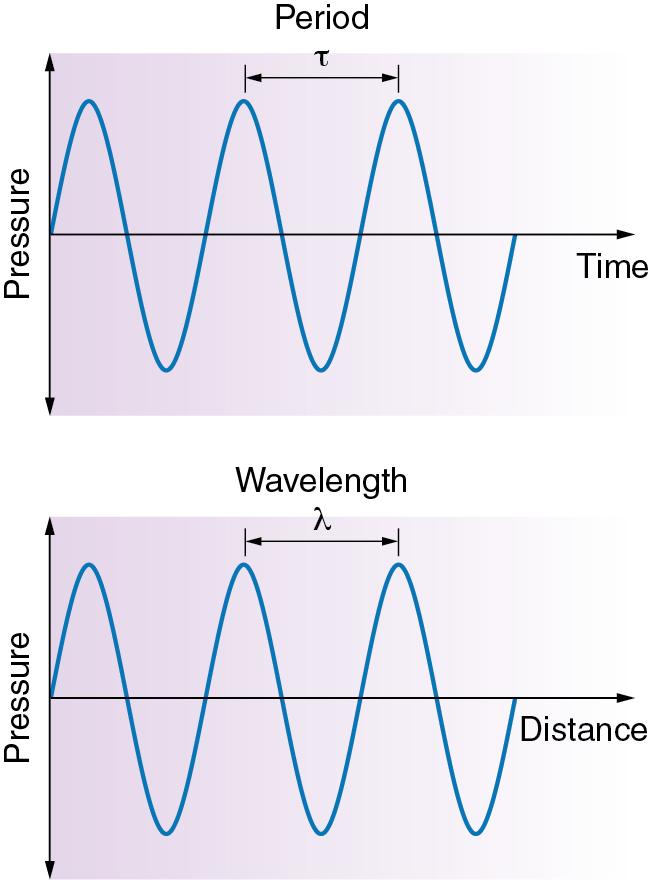
The wavelength is the distance in the propagating medium that includes one complete cycle (see Fig. 1.1 ). The wavelength (λ) is dependent on the frequency (f) of the oscillations and the velocity (c) of propagation in the medium. The relationship of wavelength, frequency, and velocity is given in Eq. 1.1 .

c = f λ

$c = f λ$

The frequency of a wave is the number of oscillations per unit of time. Typically, in ultrasound, this is stated in terms of cycles per second or Hertz (1 c/s = 1 Hz). The period of a wave (τ) is the inverse of the frequency and represents the time required to complete one cycle. The relationship between frequency and period is given in Eq. 1.2 .

c = \frac{1}{τ}

$c = \frac{1}{τ}$

The velocity of propagation depends on the physical properties of the medium in which the wave is propagating. The primary physical properties governing the velocity of propagation are the density and compressibility of the medium.

Density, compressibility, and bulk modulus

The density (ρ) of a medium is the mass per unit volume of that medium (kg/m ³ in SI units). The compressibility (K) of a medium is a property that reflects the relationship between the fractional decrease in volume and the pressure applied to a medium. For example, air has high compressibility (a small amount of pressure applied to a volume of air will result in a large fractional decrease in volume), whereas bone has relatively low compressibility (a large amount of pressure applied to a volume of bone will result in a small fractional decrease in volume). Finally, the bulk modulus (β) , which is the inverse of the compressibility, is the negative ratio of pressure applied to a medium and the fractional change in volume of the medium and reflects the stiffness of the medium.

The acoustic velocity (c) of a medium can be determined once the density (ρ) and the compressibility (K) , or bulk modulus (β) , are known. Eq. 1.3 demonstrates the relationship of the three physical properties.

Density, compressibility, and bulk modulus are not independent of one another. Typically, as density increases, compressibility decreases and bulk modulus increases. However, compressibility and bulk modulus typically vary more rapidly than does density, and they dominate in Eq. 1.3 .

c = \frac{1}{\sqrt{K_{ρ}}} = \frac{\sqrt{β}}{\sqrt{ρ}}

$c = \frac{1}{\sqrt{K_{ρ}}} = \frac{\sqrt{β}}{\sqrt{ρ}}$

The acoustic velocity in different media can be determined by applying the equations to practice. For example, water at 30°C has a density of 996 kg/m ³ and a bulk modulus of 2.27 × 10 ⁹ N/m ² . Inserting these values into Eq. 1.3 yields an acoustic velocity of 1509 m/s in water. Values for density and bulk modulus have been characterized extensively and can be found in the literature. A summary of relevant tissue properties is given in Table 1.1 . The acoustic velocity is not dependent on the frequency of the propagating wave (i.e., acoustic waves of different frequencies all propagate with the same acoustic velocity within the same medium).

TABLE 1.1

Physical Properties of Tissue

Adapted from Duck FA. Physical Properties of Tissue . London: Academic Press; 1990.

Tissue or Fluid	Density (kg/m ³ )	Bulk Modulus (×10 ⁹ N/m ² )	Acoustic Velocity (m/s)
Water (30°C)	996	2.27	1509
Blood	1050–1075	2.65	1590
Pancreas (pig)	1040–1050	2.63	1591
Liver	1050–1070	2.62	1578
Bone, cortical	1063–2017	28.13	3760

Ultrasound interactions in tissue

Ultrasound imaging of tissue is achieved by transmitting short pulses of ultrasound energy into tissue and receiving reflected signals. The reflected signals that return to the transducer represent the interactions of a propagating ultrasound wave with tissue. A propagating ultrasound wave can interact with tissue, and the results are reflection , refraction , scattering , and absorption.

Reflection

Specular reflections of ultrasound occur at relatively large interfaces (greater than one wavelength) between two media of differing acoustical impedances. At this point, it is important to introduce the concept of acoustic impedance. The acoustic impedance (Z) of a medium represents the resistance to sound propagating through the medium and is the product of the density (ρ) and the velocity (c):

Z = ρ c

$Z = ρ c$

Sound will continue to propagate through a medium until an interface is reached where the acoustic impedance of the medium in which the sound is propagating differs from the medium that it encounters. At an interface where an acoustic impedance difference is encountered, a proportion of the ultrasound wave will be reflected back toward the transducer and the rest will be transmitted into the second medium. The simplest case of reflection and transmission occurs when the propagating ultrasound wave is perpendicular (90 degrees) to the interface ( Fig. 1.2 ). In this case the percentage of the incident beam that is reflected is as follows:

• Fig. 1.2, Reflection of an ultrasound wave at normal incidence to an interface between two media with different acoustic impedances (Z).

reflected = {(\frac{Z_{2} − Z_{1}}{Z_{2} + Z_{1}})}^{2} × 100

$reflected = {(\frac{Z_{2} − Z_{1}}{Z_{2} + Z_{1}})}^{2} × 100$

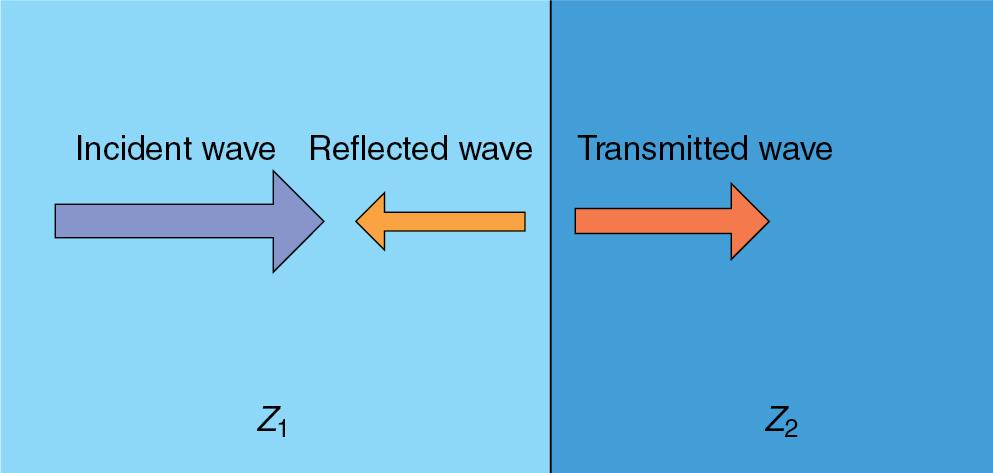
The percentage of the incident beam that is transmitted is as follows:

transmitted = 100 − reflected

$transmitted = 100 − reflected$

Refraction

When the incident beam arrives at the interface at an angle other than 90 degrees, the transmitted beam path diverges from the incident beam path because of refraction ( Fig. 1.3 ). The angle at which the transmitted beam propagates is determined by Snell’s law:

$• Fig. 1.3, Refraction and reflection of an incident wave that is not normal to the interface between media with different acoustic velocities (c). The angle of reflection is identical to the angle of incidence. The angle of the refracted wave is dependent on the acoustic velocities of the two media and can be determined by applying Snell’s law (see text).$

\frac{\sin φ_{1}}{\sin φ_{2}} = \frac{c_{1}}{c_{2}}

$\frac{\sin φ_{1}}{\sin φ_{2}} = \frac{c_{1}}{c_{2}}$

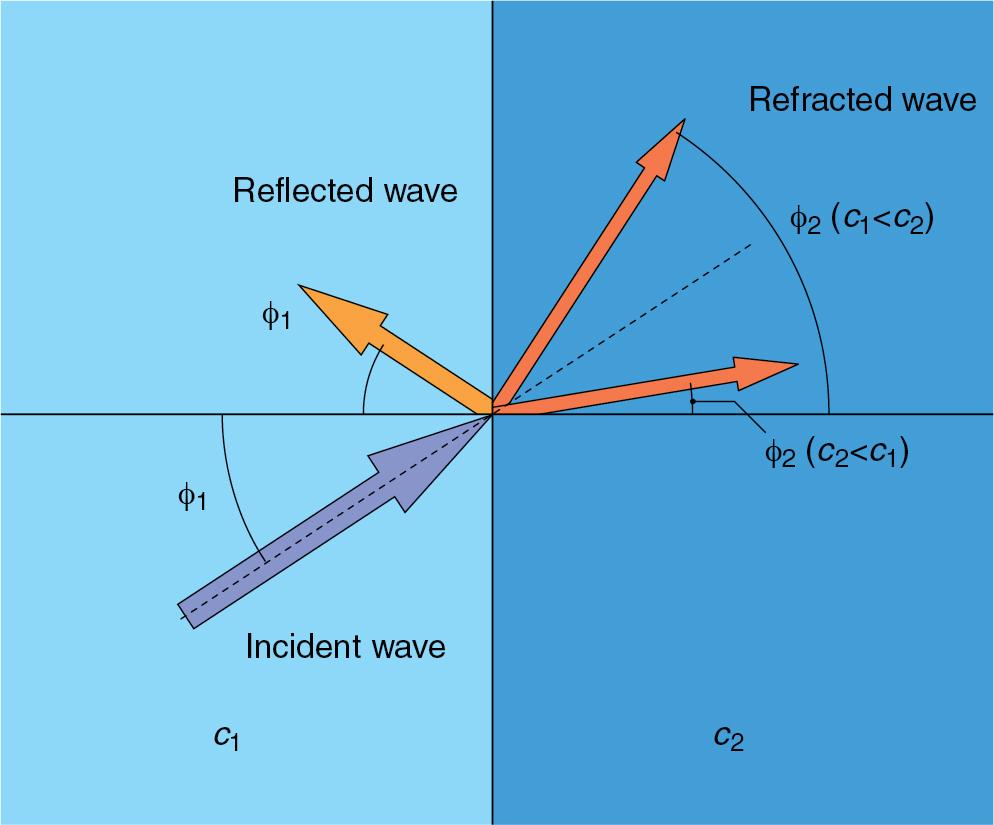
The angle of refraction is determined by the acoustic velocities in the incident ( c ₁ ) and transmitted ( c ₂ ) media. There are three possible scenarios for a refracted beam, depending on the relative speeds of sound between the two media: (1) if c ₁ > c ₂ , the angle of refraction will be bent toward normal ( φ ₁ > φ ₂ ); (2) if c ₁ = c ₂ , the angle of refraction will be identical to the angle of incidence, and the beam will continue to propagate without diverging from its path; (3) if c ₁ < c ₂ , the angle of refraction will be bent away from normal ( φ ₁ < φ ₂ ). Refraction of the ultrasound beam can lead to imaging artifacts that are discussed later in the chapter.

Scattering

Scattering , also termed nonspecular reflection , occurs when a propagating ultrasound wave interacts with different components in tissue that are smaller than the wavelength and have different impedance values than the propagating medium. Examples of scatterers in tissue include individual cells, fat globules, and collagen. When an ultrasound wave interacts with a scatterer, only a small portion of the acoustic intensity that reflects off of the scatterer is reflected back to the transducer ( Fig. 1.4 ). In addition, a signal that has undergone scattering by a single scatterer will usually undergo multiple scattering events before returning to the transducer. Scattering occurs in heterogeneous media, such as tissue, and is responsible for the different echotextures of organs such as the liver, pancreas, and spleen. Tissue containing fat or collagen scatters ultrasound to a greater degree than do other tissues, and this is why lipomas and the submucosal layer of the gastrointestinal (GI) tract appear hyperechoic (bright) on ultrasound imaging.

$• Fig. 1.4, Schematic representation of single scattering. Scattering occurs from an interface that is smaller than the wavelength of the propagating ultrasound signal. The transducer is responsible for sending and receiving the signal. I b is the backscattered intensity that will propagate back to the transducer. (A) The ultrasound signal is transmitted by the transducer and propagates toward the scatterer. (B) The pulse reaches the scatterer. (C) The incident acoustic intensity is scattered in different directions. (D) The backscattered energy received by the transducer is only a small fraction of the incident acoustic intensity that is scattered.$

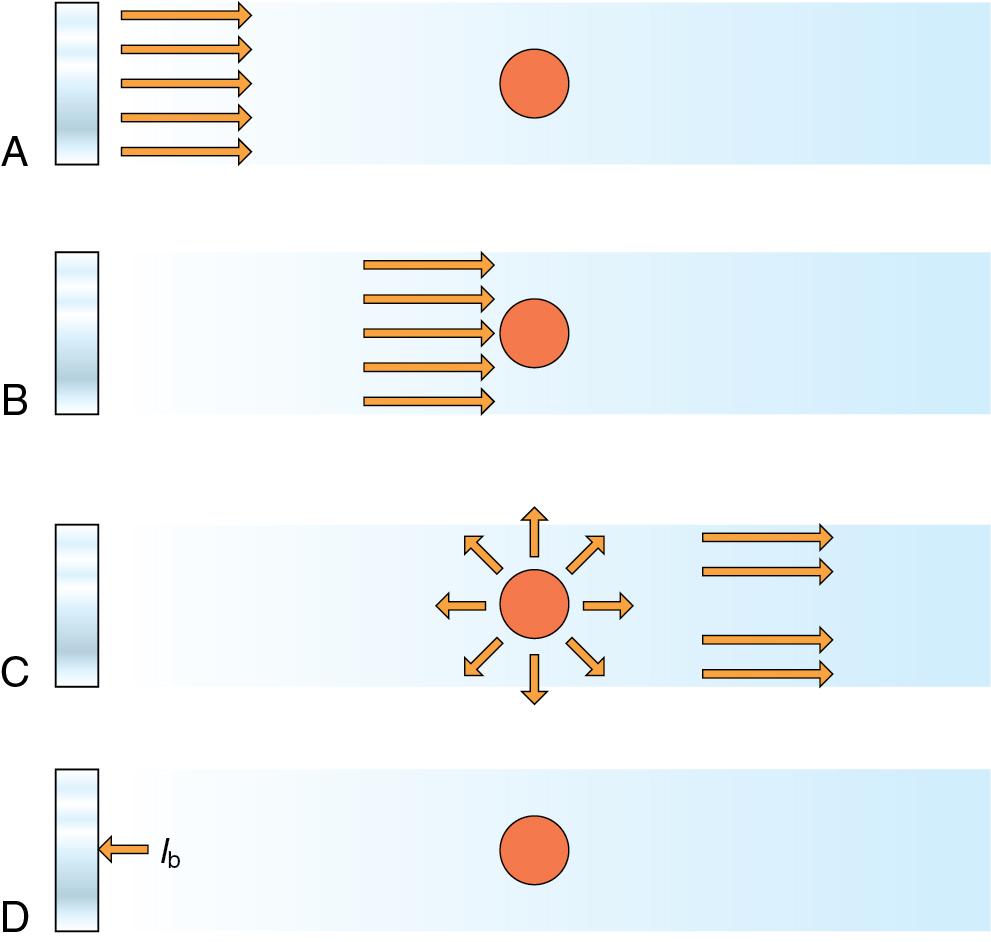
Multiple reflections from nonspecular reflectors within the tissue returning to the transducer result in a characteristic acoustic speckle pattern, or echotexture, for that tissue. Because speckle originates from multiple reflections and does not represent the actual location of a structure, moving the transducer will change the location of the speckle echoes while maintaining a similar speckle pattern. In addition, the noise resulting from acoustic speckle increases with increasing depth as a result of the greater number of signals that have undergone multiple reflections from nonspecular reflectors returning to the transducer.

Absorption

Ultrasound energy that propagates through a medium can be absorbed, resulting in the generation of heat. The absorption of ultrasound energy depends on tissue properties and is highly frequency dependent. Higher frequencies cause more tissue vibration and result in greater absorption of the ultrasound energy and more heat generation.

Ultrasound intensity

The intensity of the ultrasound signal is a parameter that describes the power of the ultrasound signal over a cross-sectional area. As ultrasound waves propagate through tissue, the intensity of the wave becomes attenuated. Attenuation is the result of effects of both scattering and absorption of the ultrasound wave. The attenuation coefficient (a) is a function of frequency that can be determined experimentally, and it increases with increasing frequency. The frequency of the ultrasound pulse affects both the depth of penetration of the pulse and the obtainable resolution. In general, as the frequency is increased, the depth of penetration decreases, owing to attenuation of the ultrasound intensity, and axial resolution improves, as discussed later in this chapter.

The intensity of the propagating ultrasound energy decreases exponentially as a function of depth and is given by the following equation:

I_{x} = I_{0} e^{− 2 a x}

$I_{x} = I_{0} e^{− 2 a x}$

where I ₀ is the initial intensity of the ultrasound pulse and I _x is the intensity of the ultrasound pulse after it has passed a distance x through tissue with an attenuation coefficient a in Neper/cm (Np/cm). As the attenuation coefficient increases with frequency, intensity also decreases exponentially as frequency increases. This equation partially explains the limitation on the depth of imaging because the returning ultrasound pulse from the tissue must be of sufficient intensity to be detected by the ultrasound transducer.

Basics of ultrasound instrumentation

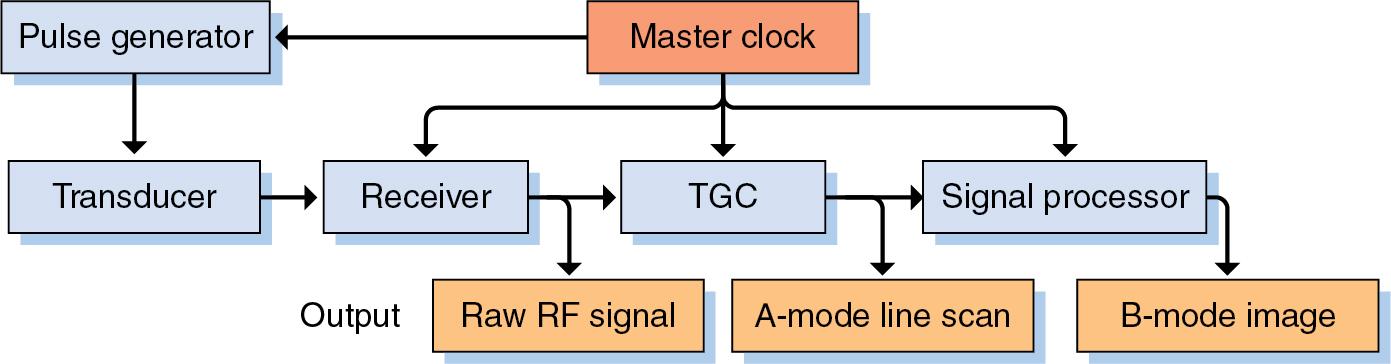
The key component of an ultrasound system is the transducer. A transducer is a device that converts one form of energy to another. In the case of ultrasound transducers, electrical energy is converted to mechanical energy, resulting in the transmission of an ultrasound pulse. When an ultrasound signal is then received by the ultrasound transducer, the received mechanical signal is converted back to an electrical signal that is then processed and digitized by the ultrasound processor to yield a real-time image of the tissue being interrogated by the ultrasound transducer ( Fig. 1.5 ).

• Fig. 1.5, Ultrasound instrumentation schematic. The overall system is synchronized by a master clock. A pulse generator sends an electrical signal to the transducer, and the result is a transmitted ultrasound pulse. The transducer then receives the backreflected signal resulting from the transmitted pulse. This signal is then passed on to the receiver, which amplifies the entire signal. The output from the receiver is the raw radiofrequency (RF) signal. The signal can then undergo time gain compensation (TGC), and the subsequent output will be the A-mode line scan. After TGC, the signal is further processed, including demodulation and registration, to yield a B-mode image.

Transducers

The active element of an ultrasound transducer, responsible for generating and receiving acoustic signals, is made typically from a piezoelectric ceramic. Piezoelectric ceramics are composed of polar crystals that are aligned in a particular orientation such that when an electric field is applied, the material changes shape. Therefore if an alternating electrical field is applied to the material at a particular frequency, the material will vibrate mechanically at that frequency, similar to an audio speaker. In addition, if the piezoelectric material is deformed by sufficient mechanical pressure (e.g., a reflected ultrasound wave), a detectable voltage will be measured across the material with a magnitude proportional to the applied pressure. The magnitude of the voltage then determines how brightly that signal is represented in B-mode imaging (this is explained in the later section on B-mode imaging).

Processors

Fig. 1.5 is a block diagram of the components of an ultrasound imaging system. The main components are the ultrasound transducer, processor, and display. Within the processor are electronic components that are responsible for controlling the excitation of the transducer, amplification of the received signal, time gain compensation (TGC), and signal processing resulting in an output signal to the display.

You're Reading a Preview

Become a Clinical Tree membership for Full access and enjoy Unlimited articles

Become membership

If you are a member. Log in here