Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
This chapter includes an accompanying lecture presentation that has been prepared by the authors: ![]() .
.
This chapter includes an accompanying lecture presentation that has been prepared by the authors: ![]() .
.
Intracranial volume is composed of cerebrospinal fluid (CSF), blood, brain, and pathologic items such as tumors or blood clots, and this volume must be constant for a given individual:
In the steady state, intracranial pressure (ICP) is mainly dependent on CSF volume and cerebral blood volume. CSF volume is highly dependent on the dural venous sinus pressure. Cerebral blood volume is dependent on cardiac parameters and cerebral autoregulation.
In the non–steady state or pathologic state, volumes of different compartments such as V BRAIN may increase.
An ICP waveform can be defined and measured. ICP indices can be measured that give information about changing compliance and autoregulation and may be able to give an early warning to worsening pathology.
Some compensation for increasing volume can occur before significant increases in ICP occur; the extent of compensation depends on the rate of change of volume (slower allows more).
Elevations in ICP reduce cerebral perfusion pressure which can limit blood flow to the brain and cause injury.
Treatment for raised ICP can follow a conceptual framework thinking about V CSF , V BLOOD , V BRAIN , and V OTHER , where different interventions tackle different compartments.
ICP therapy should be approached in a stepwise fashion, with recognition of the potential origin of the ICP elevation and observation for which treatments are more and less effective.
The exquisite sensitivity of the CNS to physical and chemical injury has led to an ingenious series of protective and homeostatic systems that shroud, nurture, nourish, and maintain maximal function. These systems include rigid physical protection in the form of skull bones, hydraulic shock absorption in the form of CSF, substrate supply and cellular homeostasis in the form of a rich vascular supply with continuous turnover of extracellular fluid, and protection from external noxious substances by the blood-brain barrier (BBB).
These highly developed protective systems can, however, become detrimental under certain pathologic conditions. In particular, encasing of the brain tissue in a rigid structure (the skull) places an important constraint on the refined interplay between cerebral homeostatic processes, namely that of volume regulation. Noncompressible matter such as fluid, when added to a rigid container, generates pressure, which in the case of the CNS is intracranial pressure (ICP). Under pathologic conditions, the intracranial volume, and therefore the ICP, can rise, a change that itself presents a serious threat to the CNS. The effects of raised ICP can further contribute to the primary pathologic process.
A wide range of neurosurgical problems—congenital lesions, neoplasms, metabolic and infectious syndromes, infarction, hemorrhage, and trauma—require evaluation and treatment for elevated ICP. Effective clinical treatment of problems relating to raised ICP demand a detailed understanding of the physiologic mechanisms that generate and maintain normal ICP, perturbations that lead to an elevated ICP, and means by which elevated pressures can be reduced.
Although problems with brain swelling and the effects of removing pieces of skull were understood even in the times of Galen, Hippocrates, Mesoamerica cultures, and the early Egyptian physicians, modern thinking about volume regulation inside the skull began with the writings of George Kellie and his mentor Alexander Monro, who worked in Edinburgh at the turn of the 19th century. Monro, in his seminal work on the brain and nervous system wrote :
For, as the substance of the brain, like that of other solids of our body, is nearly incompressible, the quantity of blood within the head must be the same, or very nearly the same at all times, whether in health or disease, in life or after death, those cases only excepted in which water or other matter is effused, or secreted from the blood vessels; for in these a quantity of blood, equal in bulk to the effused matter, will be pressed out of the cranium.
Some years later at a meeting of the Medico-Chirurgical Society of Edinburgh, George Kellie presented a report in which he advanced this idea and stated :
If these premises be true, it does not then appear very conceivable how any portion of the circulating fluid can ever be withdrawn from within the cranium, without its place being simultaneously occupied by some equivalent; or how anything new or exuberant can be intruded without an equivalent displacement.
These ideas, which were formalized physiologically later, became known as the Monro-Kellie doctrine. Subsequent advances in the understanding of ICP came with the ability to effectively monitor ICP under different circumstances. Quinke first described lumbar puncture for the relief of “brain pressure” in 1911. However, it was not until the work of Guillaume and Janny in 1951 that ICP began to be continuously monitored. Lundberg later published results from a large series of patients in which he described several of the fundamental concepts used today in clinical ICP monitoring, including the Lundberg A, B, and C waves.
ICP monitoring today is considered commonplace in neurosurgical practice. ICP values are used as a measure of disease and an indication of treatment response as well as to assist with monitoring cerebral perfusion.
The upper limit of normal ICP in adults and older children is given as 15 to 20 mm Hg. “Normal” values for ICP depend on age, body posture, and clinical conditions. In the supine position, ICP in healthy adults is reported as 7 to 15 mm Hg. In the vertical position, it may become negative (as low as –15 mm Hg). Transient physiologic changes resulting from coughing or sneezing often produce pressures exceeding 30 to 50 mm Hg, but ICP returns rapidly to baseline levels.
ICP can be measured with the use of low-volume displacement transducers to interface with CSF pathways in the intraventricular, intraparenchymal, subdural, or epidural space. The ICP waveform is normally pulsatile and can be divided into three major components ( Fig. 69.1 ). The average level is commonly referred to as the ICP, whereas rhythmic fluctuations in pressure superimposed on this level are associated with cardiac and respiratory activity. To completely describe ICP, one should specify the magnitude of the baseline, or “steady-state” level and the amplitude and periodicity of the pulsatile components. Changes in these pulsatile components can be one of the earliest signs that the ICP is beginning to rise, as a reflection of the increased conductance of pressure waves through a “tightening” brain.
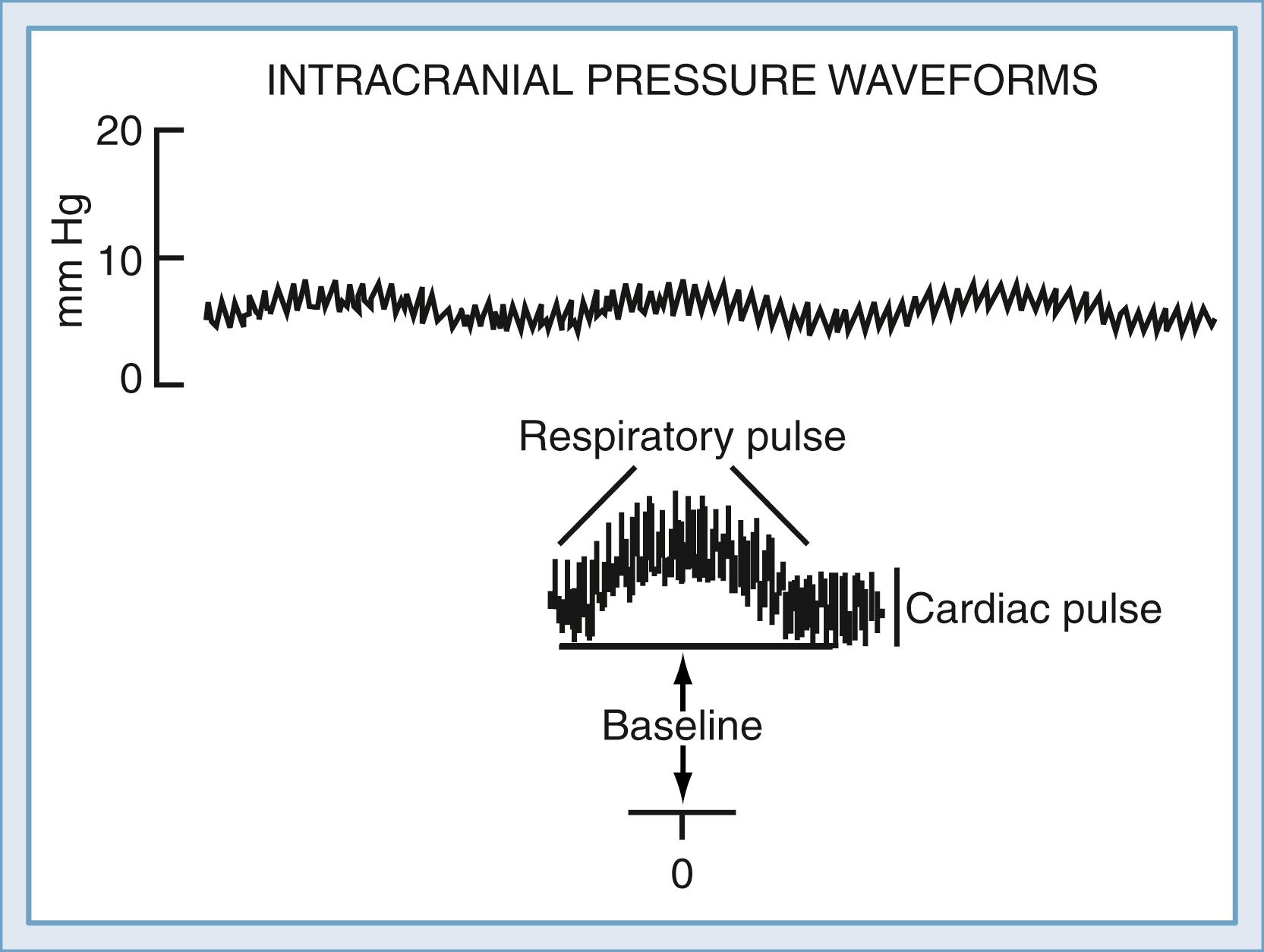
Cardiac and respiratory activity creates pulsatile components via cyclical changes in cerebral blood volume (CBV). Left ventricular contraction contributes the cardiac component, which has a frequency similar to that of the peripheral arterial pulse. The exact vessels that transmit the peripheral pulse remain to be established. Early studies suggested that the choroid plexus and pial arteries were responsible, although later analysis has implicated the high-compliance venous blood vessels.
The respiratory contribution to the ICP waveform arises as a result of fluctuations in arterial blood pressure and cerebral venous outflow during the respiratory cycle, generated by pressure changes in the thoracic and abdominal cavities. During inspiration, there is a fall in arterial blood pressure and an increase in pressure gradient from the cerebral veins to the central venous capacitance vessels. This gradient drives cerebral venous return, which is therefore increased on inspiration, with a concomitant drop in total CBV. Mechanical ventilation and intrathoracic disease may considerably alter the respiratory contribution to the ICP waveform. This concept has resulted in experimental and clinical trials of devices that can alter intrathoracic pressure during the respiratory cycle of resuscitation. The impedance threshold device limits inflow of respiratory gas and therefore creates greater and longer negative intrathoracic pressure. The device has been shown to improve cerebral and coronary perfusion and to reduce ICP in cardiac arrest and hypotension. , Its application to or effect on elevated ICP in primary CNS disease such as traumatic brain injury is yet to be determined, although early human studies have suggested that ICP may be reduced by its use. The complex relationship among pulmonary function, intrathoracic pressure, and ICP can lead to considerable challenges when managing concurrent lung and brain injury in the polytrauma population.
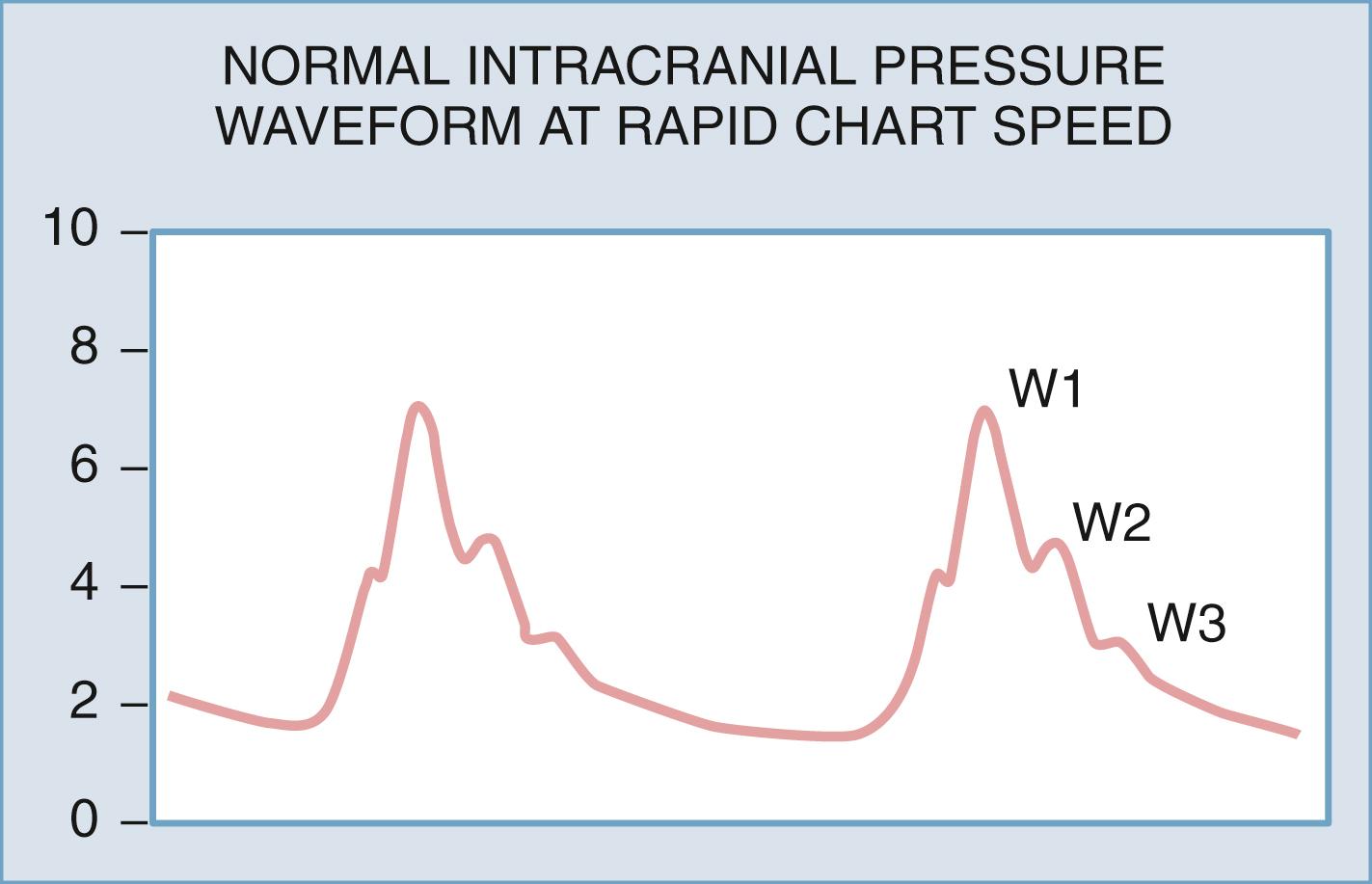
If the ICP waveform is examined in more detail and at higher resolution, then the waveform of highest frequency can be seen to consist of as many as five smaller peaks. Three of these are relatively constant ( Fig. 69.2 )—the percussion wave (W1), the tidal wave (W2), and the dicrotic wave (W3). , The percussion wave, the most constant in amplitude, derives from pulsations in large intracranial arteries. The tidal wave has a more variable shape and is thought to arise from brain elastance. The tidal wave and the dicrotic wave are separated by the dicrotic notch, which corresponds to the dicrotic notch in the arterial pulse waveform.
As the intracranial space approximates a fluidic space, ICP is functionally synonymous with CSF pressure and is defined as the pressure that must be exerted against a needle introduced into the CSF space so as to just prevent escape of fluid. ICP depends on several parameters that are features common to any hydrodynamic system: the internal (intracranial) fluid volume, the elastance of the system, the contribution from the atmosphere, and the orientation of the craniospinal axis relative to the gravitational vector.
Pressure (P) is defined as force (F) per unit area (A). Pressures are usually reported in units of either millimeters of water (mm H 2 O) or millimeters of mercury (mm Hg). This convention arose because a fluid column exerts a pressure at its base proportional to the height of the column (h), the density of the fluid (ρ), and the gravitational constant (g). Because, for a given fluid, g and ρ are constant, pressures can be compared by their relation to the height of a given fluid. ICP is thus variably expressed in either mm Hg or mm H 2 O. Dividing the pressure in mm H 2 O by 13.6 yields the equivalent pressure in mm Hg; this constant is based on the ratio of the density of water to mercury. The SI unit for pressure is the Pascal (Pa), which is defined as 1 Newton (N)/square meter. One kiloPascal (kPa) is 7.5 mm Hg or 102 mm H 2 O.
In actual fact, three different pressures contribute to ICP: atmospheric pressure, hydrostatic pressure, and filling pressure. Atmospheric pressure is the component resulting from pressure in the atmosphere that is transmitted to the brain, and therefore absolute ICP varies with altitude. This pressure is principally transmitted through the vasculature ; however, ICP is typically reported relative to atmospheric pressure, and this latter component is ignored.
As with any column of fluid, the skull and spinal canal experience hydrostatic pressure caused by the weight of their contents. The contribution of hydrostatic pressure depends on the weight of fluid and tissue above the point of measurement, divided by the cross-sectional area at that level. For example, lumbar CSF is greater in the sitting position than in the lateral decubitus position , as a result of the hydrostatic difference; increasing degrees of head-down tilting further increase the contribution of hydrostatic pressure.
The filling pressure of the system is determined by the volume of the intracranial contents and the elastance of the enclosing structures. The intracranial contents consist of blood, brain, CSF, and any pathologic masses. As an enclosed system, the relationship of intracranial contents can be approximated as a fixed volume.
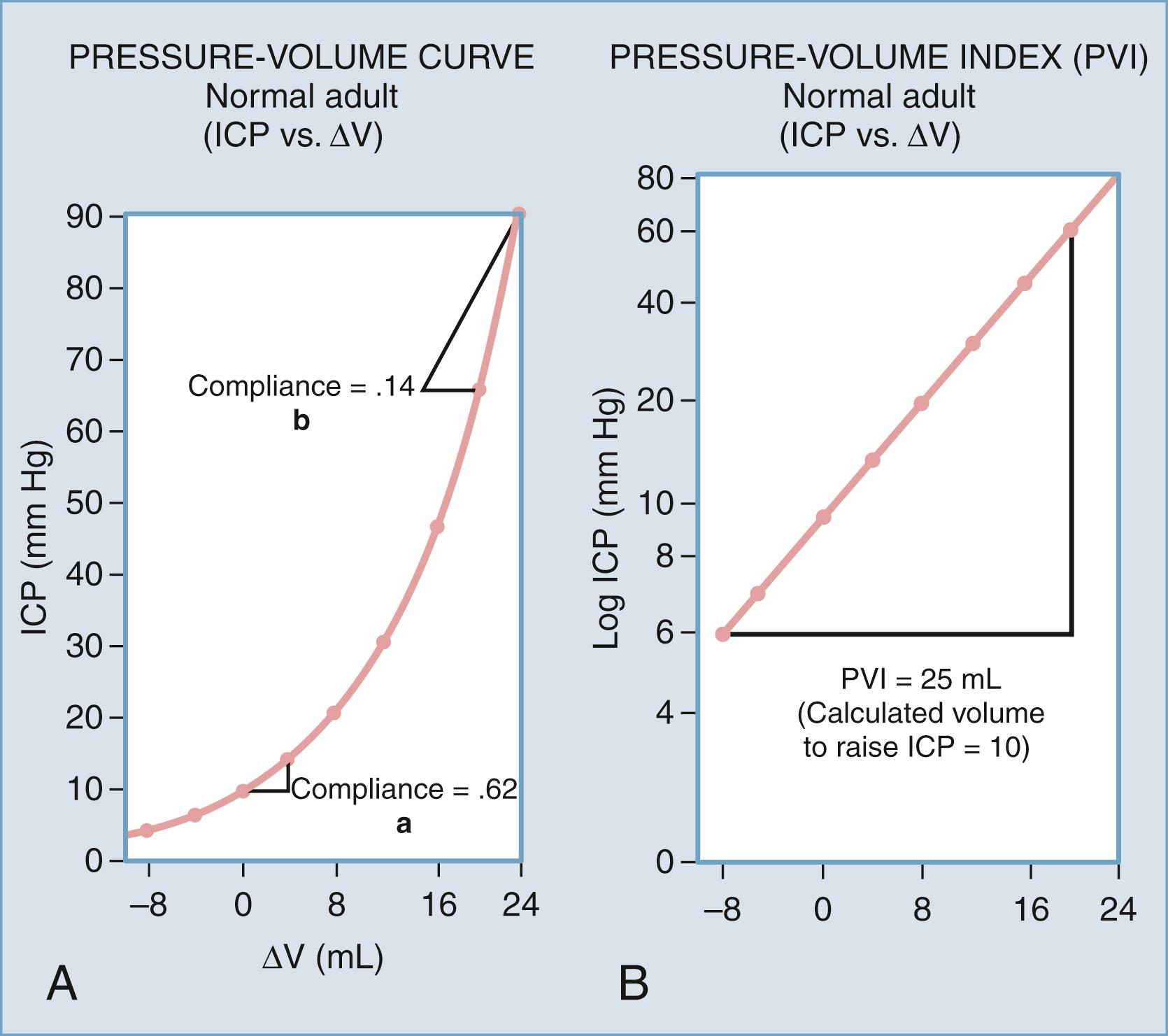
However, in the non-ideal in vivo environment, the described volumes are subject to differences in tissue characteristics such as elastance and compliance. Elastance is a system parameter that is defined by the pressure change per unit of volume change, that is, the corresponding pressure change for any given volume increase in craniospinal contents ( Fig. 69.3 ). The relationship is not necessarily linear across all volumes and not necessarily constant under all physiologic conditions. Compliance is the inverse of elastance, and both measures are useful for understanding the physiology of ICP. Elastance arises as a combined result of both distention and displacement. In other words, as volume is added to the system, there are two principal routes for compensation, expansion, and loss of volume. In a physiologic sense, this can occur either by distention of the spinal dura mater or by displacement of CSF and blood. These concepts will be expounded upon in the discussion of non–steady-state dynamics later in this chapter. Atmospheric pressure, hydrostatic pressure, and filling pressure all contribute to the concept of steady-state dynamics.
In the adult, approximately 87% of the typically 1500-mL intracranial space is occupied by the brain, 9% by compartmental CSF (ventricles, cisterns, and subarachnoid space), and 4% by blood. The extracellular space is in direct contact with the CSF and forms approximately 15% of the total brain volume. Total CSF is considered to include compartmental CSF and the extracellular space.
Cranial CSF volume as assessed in humans was found to have a mean of 164.5 mL, with a range of 62.2 to 267 mL. Ventricular volume also varies considerably as assessed with MRI, from 7.49 to 70.5 mL, with a mean of 31.9 mL. Reasons for such variation are not clear, although the amount of CSF in any organism reflects a dynamic balance between production and clearance.
CSF is classically considered to have been produced principally by the choroid plexuses, which are invaginations of the pia mater into the ventricular cavities, specifically in the roofs of the third and fourth ventricles and the walls of the lateral ventricles. At these points, fronds of densely branching blood vessels are invested by pia mater and covered by specialized ependymal cells, the choroidal epithelium. The surfaces of cells in this structure are densely covered with villous processes to increase the surface area. A second site of CSF production is the ventricular ependyma, the proportional contribution of which arguably ranges from 50% to 100%. ,
For a considerable time, CSF was described as an ultrafiltrate of plasma, implying that hydrostatic pressure within blood vessels forced protein-free fluid through interendothelial spaces. Close analysis of the composition of CSF ( Table 69.1 ), however, shows multiple differences in composition at the ionic level, a finding that argues strongly against the idea of a simple filtration or dialysis process. CSF, in general, has higher sodium, chloride, and magnesium concentrations than one would expect in a plasma filtrate. The concentrations of potassium, calcium, urea, and glucose are lower. The overall osmolality is, however, very similar. Current thinking therefore holds that a simple filtration process is modified by energy-dependent secretion and reabsorption processes.
| Substance | Plasma | CSF |
|---|---|---|
| Sodium (Na + ) | 150 | 147 |
| Potassium (K + ) | 4.63 | 2.86 |
| Magnesium (Mg 2+ ) | 1.61 | 2.23 |
| Calcium (Ca 2+ ) | 4.7 | 2.28 |
| Chloride (Cl − ) | 99 | 113 |
| Bicarbonate (HCO 3 − ) | 26.8 | 23.3 |
| Amino acids | 2.62 | 0.72 |
| Osmolality | 289.0 | 289.0 |
| pH | 7.397 | 7.30 |
Estimates of the rates of CSF production can be made experimentally through examination of the clearance or turnover of injected substances, by marker dilution techniques, or by ventriculocisternal perfusion. Estimates with these techniques have yielded values in the range of 0.35 to 0.37 mL/min for humans. , In later studies, flow voids in MR signal within the CSF system have been used to estimate CSF production rates. Estimates of the flow of CSF through the aqueduct in humans, which should in principal equate to the flow of CSF secretion in the lateral and third ventricles, have yielded values of 0.48 mL/min. There are variations in absolute rates of CSF production, though, that clearly relate to the absolute weight of CSF producing tissue in each subject. Furthermore, rates of CSF production follow a diurnal variation, with peak production rates in the late evening and early morning.
Because there is a constant production of CSF, there must be removal of CSF at the same rate. CSF circulates from its origin, through the ventricles, to the cisterna magna, basal cisterns, and subarachnoid space. The principal site of physiologic CSF drainage is into the dural venous system through the dural venous sinuses. Evaginations of the arachnoid membrane protrude into the lumens of the dural veins and form the arachnoid granulations or villi. This arrangement forms a valvular connection between the subarachnoid space and the dural sinus so that blood cannot reflux into the CSF. A higher hydrostatic pressure in the subarachnoid space drives the bulk flow of fluid in the forward direction, therefore draining CSF volume. Studies of these structures have revealed that they can allow molecules up to several microns to pass, but only unidirectionally. CSF reabsorption has been shown to cease at CSF pressures less than 5 mm Hg. Additional pathways of solute flow have been demonstrated including lymphatics of the nasal mucosa, transporters and receptors in the choroid plexus epithelium, and meningeal lymphatic vessels. The relative contribution of these routes in the human population is unknown.
In the absence of pathology, baseline ICP and the amplitude of the pulsatile components of ICP remain constant despite a variety of transient perturbations. As alluded to previously, the skull should be regarded as a rigid container of noncompressible elements. ICP therefore depends on the relative constancy of total volume inside the skull (V INTRACRANIAL SPACE ), contributed to by cerebrospinal fluid (V CSF ), blood (V BLOOD ), and brain tissue (V BRAIN ). The ability of the dural coverings to distend is very limited, so any change in volume of one of the three intracranial components must occur at the expense of the other two if ICP is to be maintained. The following equation describes this relationship:
This relationship encapsulates the concept of the Monro-Kellie doctrine. The presence of an abnormal component such as a tumor or hematoma (represented by V OTHER in the preceding equation) demands reciprocal change(s) in the volumes of brain, blood, or CSF to maintain ICP at physiologic levels. It is important to note that even the physiologic state is far from static; it is rather a dynamic equilibrium. Constant changes induced by the heartbeat, systemic blood pressure, fluid status, and intrathoracic pressure invoke transient changes within the intracranial compartment that are considered part of the steady state.
As alluded to previously, the nonpulsatile volume of CSF at any point in time depends on a balance among rate of formation, rate of absorption, and the volume sink in the skull. The interactions among these parameters can be addressed with use of a mathematical model that analyzes the physiologic mechanisms of (1) CSF formation; (2) volume storage, or compliance; and (3) fluid absorption ( Fig. 69.4 ).
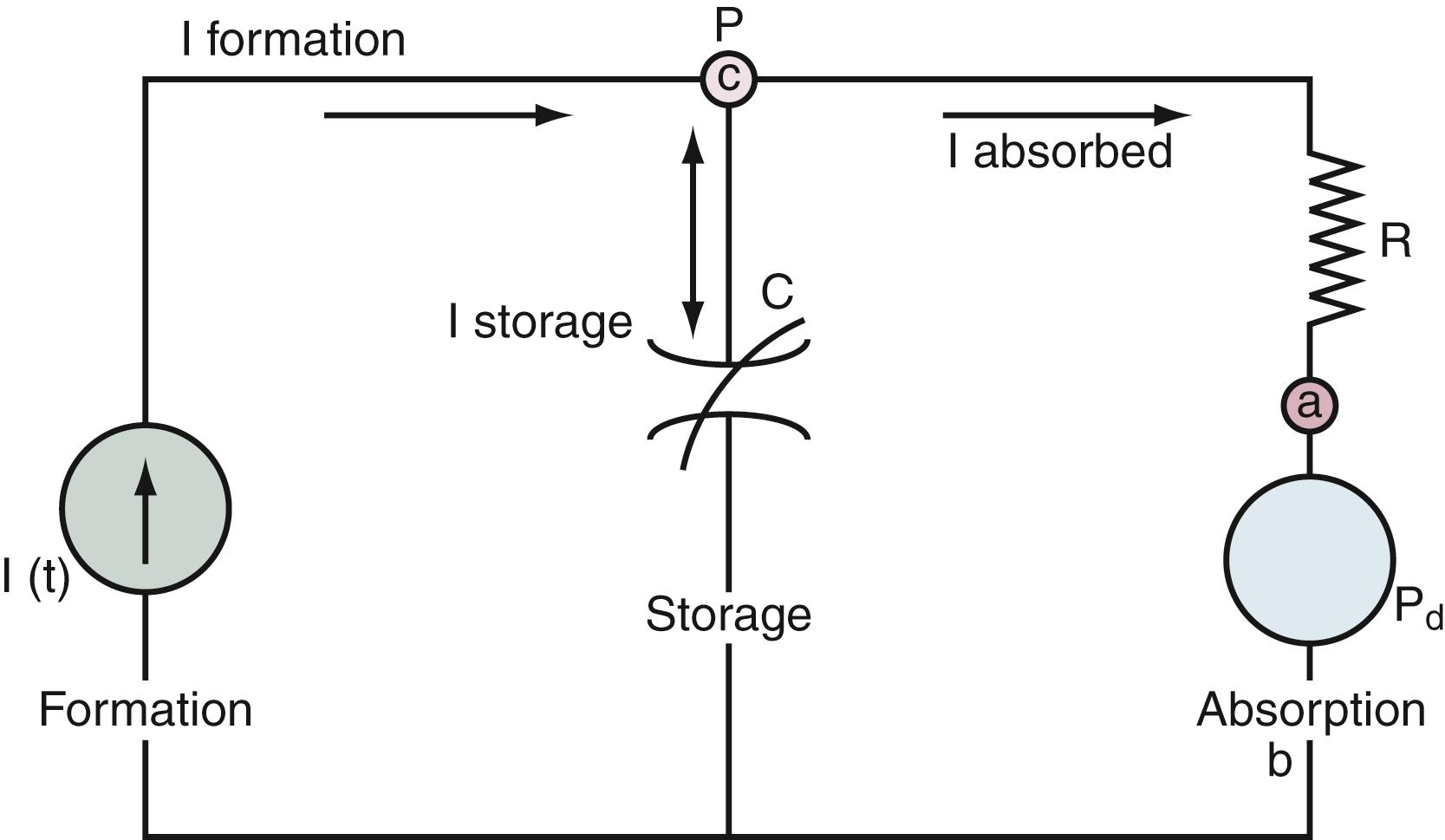
The formation of CSF can be depicted as a pump that continuously introduces fluid into the CSF spaces of the neural axis. The rate of formation of fluid (I f ) is considered constant and independent of the pressure that has to be pumped against, in accordance with observations that the rate of CSF formation is affected minimally, if at all, by changes in the ICP. The fluid enters a compliant storage space, which can expand to accommodate the added volume, and proceeds via outflow pathways to be absorbed across the arachnoid villi into the dural venous sinuses. The compliance mechanism is represented by an element (C) that decreases its compressibility with increasing volume, much like the resistance offered by a rubber balloon at maximum inflation. Both the resistance of the CSF channels leading to the arachnoid villi and the resistance of the villi to fluid flow are combined into a single resistive element (R o ). This component represents the total resistance to the outflow of CSF, which under normal conditions remains fixed and independent of ICP. The final element of this model is the dural sinus pressure (P d ). Fluid crossing the arachnoid villi must overcome this exit pressure.
From this conceptual framework, a theory has been developed to describe the interaction of the formation, storage, and absorptive elements in the steady state. First, both pressure and volume are in equilibrium, and there can be no net increase or decrease in the total volume of CSF. The CSF formed must pass through the absorptive elements so that no net fluid is stored.
Because all fluid formed passes through the resistive element (R o ), a pressure gradient is developed across the absorptive element that is equal to the product of fluid formation (I f ) and fluid resistance (R o ). The greater the magnitude of flow or resistance, the greater the resulting pressure gradient (I f × R o ). As long as the system is in equilibrium, the pressure of the CSF spaces must be of sufficient magnitude to drive fluid through the arachnoid villi at the same rate it is being formed. Therefore, the CSF pressure (ICP) must be equal to the sum of the pressure gradient across the absorptive element (I f × R o ) and the exit pressure. The following equation
shows that the steady-state ICP is proportional to three parameters: (1) the rate of CSF formation, (2) the resistance to CSF absorption, and (3) the dural sinus pressure. When these parameters remain constant, ICP is unchanged and the compliance element does not actively participate in ICP regulation. This relationship can be visually expressed as an equivalent electrical circuit (see Fig. 69.4 ).
An increase in CSF formation, outflow resistance, or venous pressure at the site of fluid absorption can alter this dynamic equilibrium and result in elevated ICP. Mathematical modeling has shown that the contribution of the product of CSF formation rate and outflow resistance (I f × R o ) is approximately 10% of the total ICP. The remainder is attributed to the magnitude of the dural sinus pressure (P d ). With this distribution, the outflow resistance would have to increase markedly to cause a significant rise in ICP. However, much smaller elevations of sagittal sinus pressure (P d ) caused by venous sinus obstruction would be transmitted directly to the CSF system, thus raising resting ICP. From the preceding equation, it is clear that changes in these elements can occur independently of one another. If P d rises, CSF absorption can remain constant, and a shift to a new ICP equilibrium can occur. Normal CSF resistance in the presence of raised ICP induced by venous obstruction has been demonstrated. In this case, there is no net change in the CSF volume and presumably no change in the compliance element.
The other dynamic component of the equation representing the Monro-Kellie doctrine that is relevant in steady-state dynamics is CBV. CBV and CBF are essentially functions of the cerebral arteriovenous pressure difference and cerebrovascular resistance, which is largely determined by vessel caliber. Although, as described previously, there are rhythmic changes in blood volume as a result of the cardiorespiratory cycles, both CBV and CBF are maintained within narrow limits by the process of autoregulation. Vascular tone is influenced by both physical (biomechanical force) and chemical (pH, P co 2 ) signals, with the aim of maintaining CBF across a wide range of both arterial blood pressures (50 to 160 mm Hg) and levels of tissue metabolism (Pa co 2 , 20 to 70 mm Hg). The mean normal adult CBF is 53 mL/100 g per minute.
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here