Neonatal Pulmonary Physiology

Lung Volumes and Lung Mechanics

Knowledge of the functional components of lung volume and the mechanical properties of the lungs plays an important role in the understanding of neonatal respiratory physiology. The lungs have physical and mechanical properties including elastic recoil, airway resistance and inertance that resist inflation. The dynamic interactions between these properties are responsible for the effort required during normal spontaneous tidal breathing. A driving pressure is required to move a volume of gas into and out of the respiratory tract during a respiratory cycle that results in measurable airflow and volume changes. Functional residual capacity (FRC) is the volume of air in the lungs at the end of expiration of a normal, resting breath when alveolar pressure ( P _A ) equals atmospheric pressure ( P _atm ; Fig. 39.1A ). Establishment of the FRC is vital to maintain adequate lung mechanics and gas exchange. FRC is maintained by the opposing forces of lung elastic recoil and chest wall outward recoil. Changes in the elastic properties of either the lung or the chest wall alter FRC.

Respiratory System Compliance

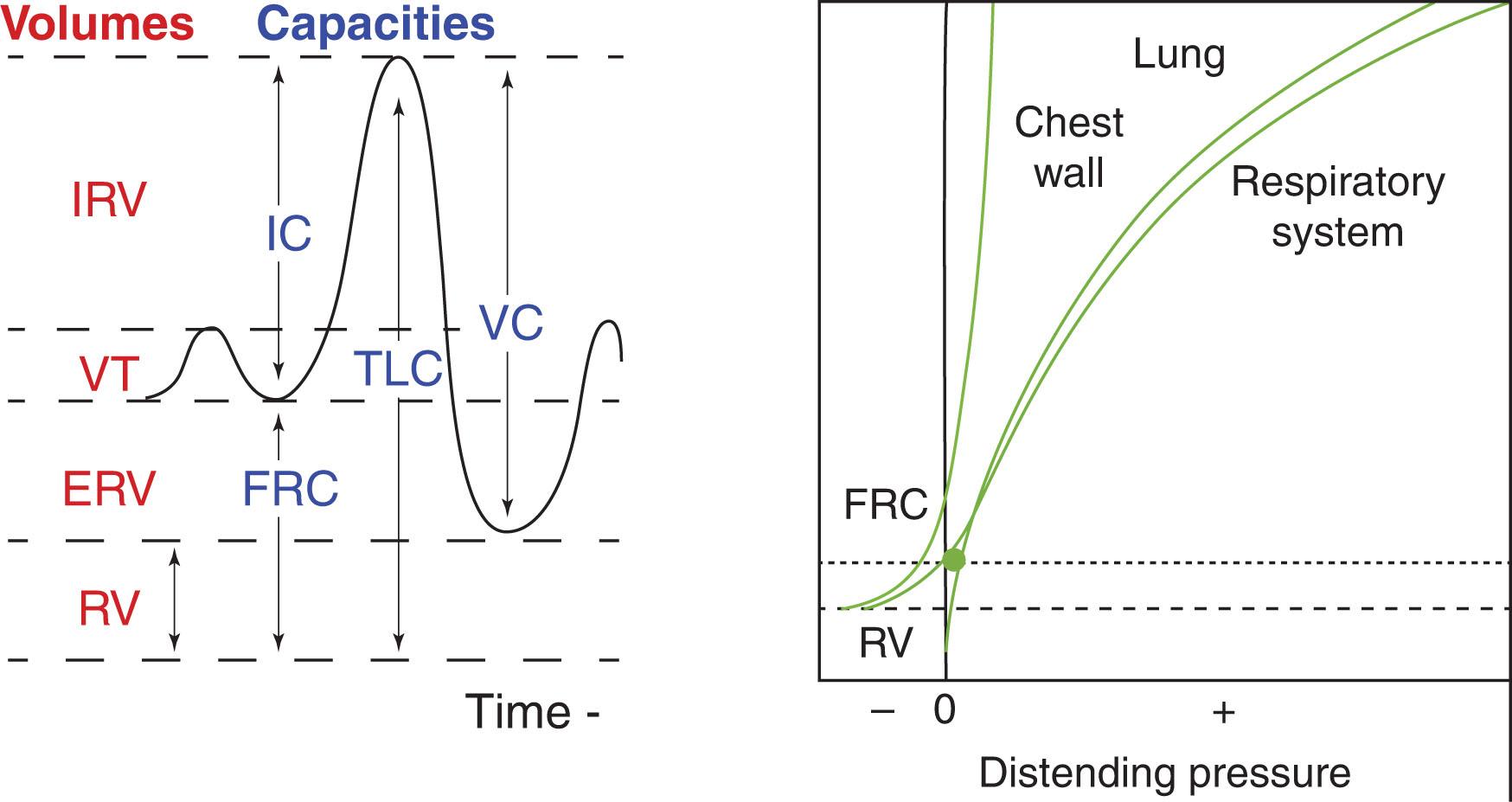
The lung contains elastic tissues that pull the lung to its deflated state. This property is called elastic recoil. Hooke’s law requires that the pressure needed to inflate the lungs must be in proportion to the volume of inflation. The change in volume divided by the change in pressure is the lung compliance ( Fig. 39.1B ).

Conventionally, the volume of inflation is plotted on the y -axis, and the distending pressure is plotted on the x -axis. In this way the constant of proportionality is volume divided by pressure, or lung compliance. Throughout the range of tidal breathing the relationship between pressure and volume is linear. At higher lung volumes, as the lung reaches its elastic limit (i.e., total lung capacity), this relationship plateaus, making the pressure–volume relationship nonlinear. Static compliance is the change in volume for a given pressure during static, non flow conditions. On a static compliance curve, ventilation occurs at the steep portion where large changes in volume occur for small changes in pressure. Dynamic compliance is the change in volume and pressure during spontaneous or mechanical breathing while there is airflow. It is predominantly influenced by the rate of respiration.

The total compliance of the respiratory system ( C rs ) is comprised of the compliance of the lung ( C l ) and chest wall ( C cw ), where 1/ C rs = 1/ C l + 1/ C cw . The tendency for the lung to collapse inward at the end of exhalation is balanced by the negative (subatmospheric) intrapleural pressure resulting from the outward recoil of the chest wall. FRC is maintained when these opposing forces are at equilibrium. Inflation of the respiratory system above FRC requires a positive distending pressure that must overcome the elastic recoil of both the lung (alveolar pressure minus intrapleural pressure) and the chest wall (intrapleural pressure minus atmospheric pressure). Deflation below FRC requires an active expiratory maneuver. Residual volume (RV) is defined as the volume of air that cannot be expired even with a forced deflation.

As depicted in Fig. 39.1B the infant's chest wall is composed primarily of cartilage. Therefore, C cw is greater in infants, and the pleural pressure is less negative or only slightly sub atmospheric. As a result of the more compliant chest wall with very little outward distending pressure, the neonatal lung is more prone to collapse at the end of exhalation. In newborn infants, FRC is maintained during spontaneous breathing by increasing expiratory resistance through laryngeal adduction (glottic narrowing), by maintaining inspiratory muscle activity throughout expiration, making the chest wall stiffer, and by initiating high breathing frequencies to limit the expiratory time, and causing the lungs to retain gas (gas trapping).

Airway Resistance

A gradient of pressure (Δ P ) is required for gas flow ( V ) to occur to overcome the nonelastic resistance of the lungs. Mathematically, resistance ( R ) = (Δ P )/ V . Physical resistance to gas flow arises due to friction between gas molecules against the walls of airways (i.e., airway resistance) and due to friction between the tissues of the lung and the chest wall (i.e., viscous tissue resistance). Resistance depends on the length and diameter of the airway as well as the density and viscosity of the gas. Airway resistance represents approximately 80% of the total resistance of the respiratory system; tissue resistance and inertial forces account for the remaining 20%. In the newborn, the small size of the airways makes them significantly more prone to high airway resistance with nasal resistance representing almost half of the total airway resistance. In addition, neonates are preferential nose breathers. Therefore, any mucus or edema in the nasal passages can offer significant resistance to air flow.

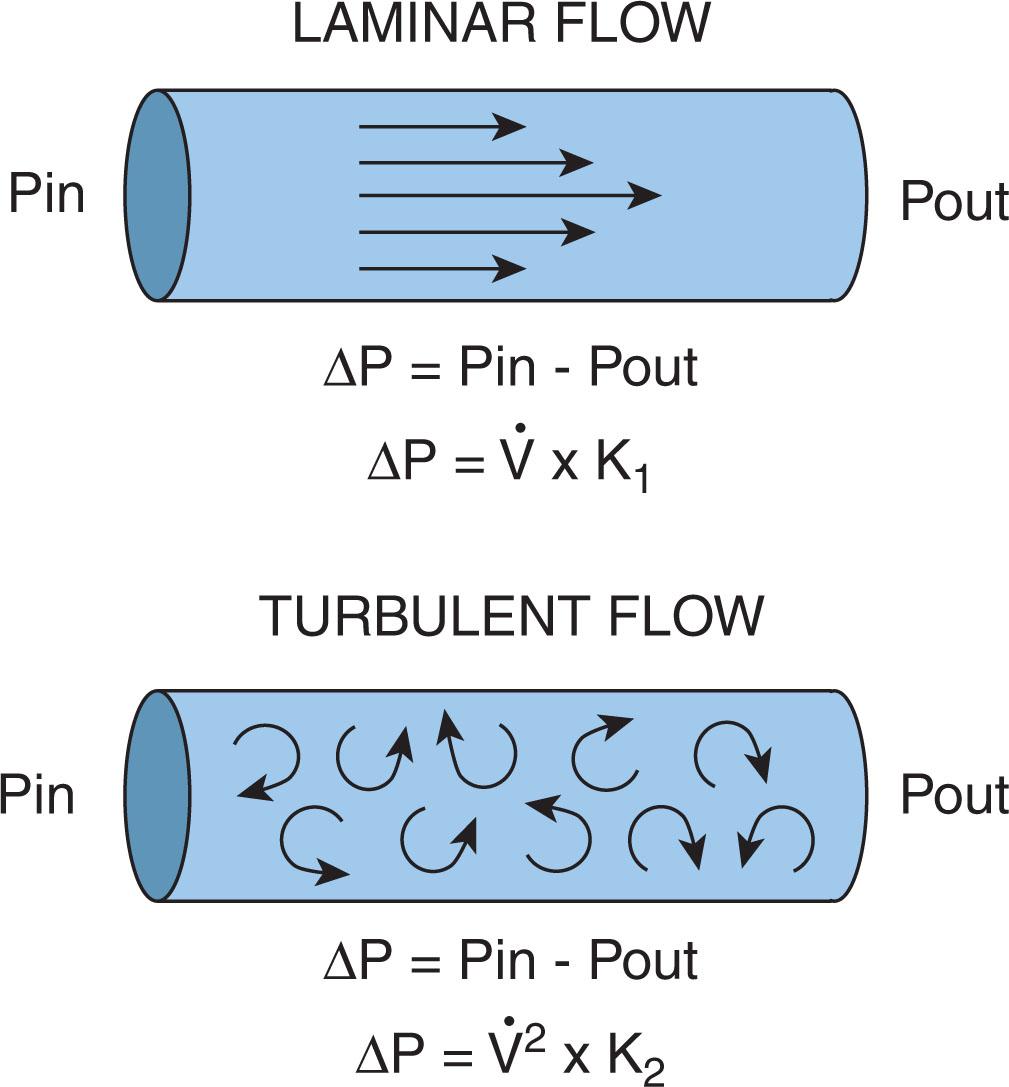
The movement of gas through the airway is modeled by two basic patterns of flow, laminal and turbulent ( Fig. 39.2 ). During laminar flow the pressure difference needed to move gas through the airway is directly related to the flow rate times a constant (airway resistance). During turbulent flow, however, this pressure is directly proportional to a constant multiplied by the flow rate squared. Gas flow becomes turbulent at branch points in airways, at sites of obstruction, and at high flow rates. Turbulence occurs whenever flow increases to a point that the Reynolds number exceeds 2000. This dimensionless number is derived from fluid dynamics and is calculated as Re = [ p × d × V ]/[ u ] where V is the volumetric flow rate, p is gas density, d is radius of the tube, and u the gas viscosity. Obviously, turbulent flow is most likely to occur in the central airways, where volumetric flow is high, rather than in peripheral airways where flow is distributed across a large total cross-sectional area. Both types of flow exist in the lung, so the net pressure drop is calculated as follows :

Inflation of the lung increases the length of airways and might therefore be expected to increase airway resistance; however, lung inflation also increases airway diameter. Because airway resistance varies with the fourth to fifth power of the radius of the airway, the effects of changes in airway diameter dominate, and resistance is inversely proportional to lung volume. Airway resistance is lower during inspiration than during expiration, because pleural pressure becomes more negative during inspiration, and a greater distending pressure is applied across the lung. This distending pressure increases airway diameter as well as alveolar diameter and decreases the resistance to gas flow. During expiration, pleural pressure increases and airways are compressed. Collapse of airways is opposed by their cartilaginous support and by the pressure exerted by gas in their lumina. During passive expiration these defenses are sufficient to prevent airway closure. When intrapleural pressure is high, during active expiration, airways may collapse, and gas may be trapped in the lung causing dynamic hyperinflation. This problem may be accentuated in the small preterm infant with poorly supported central airways.

Inertance

Gas and tissues in the respiratory system also resist accelerations in flow, which is determined by gas density and the ratio of airways length to surface area. Inertance represents opposition to these accelerated forces and is assumed to be negligible during quiet breathing and physiologically significant only at rapid respiratory frequencies and high flow rates.