Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
The human infant has at least two important advantages over the adult in the evaluation of respiratory mechanical function. First, the infant, like newborn mammals of many species, is often asleep and does not immediately react to gently performed maneuvers. Hence, a maneuver consisting of a very brief occlusion of the airways during spontaneous breathing is often used in the evaluation of the mechanical properties of the respiratory system in infants. Second, infants have a chest wall compliance ( C w ) some five times higher than lung compliance ( C L ). Therefore because the reciprocal of respiratory system compliance 1/ C rs equals 1/ C L + 1/ C w , C rs is about 83% of C L . This means that C rs essentially reflects C L in infants, which is an important practical advantage because C rs can be measured much more easily than C L . This chapter reviews some basic concepts and focuses on simple techniques that permit measurements of respiratory mechanics in newborn infants.
In the chain of events that contribute to the translation of the output of the respiratory rhythm generator into pulmonary ventilation, the mechanical properties of the respiratory system are a critical aspect ( Fig. 63.1 ). After activation of the inspiratory muscles, the magnitude of the force generated depends on the force-length and force-velocity characteristics of the muscles. The physical translation of force into inspiratory pressure depends on the configuration of the muscle and the mechanical properties of the structure to which the force is applied. Finally, of the total muscle pressure generated, a part overcomes the elastic properties of the respiratory system to change lung volume (V) and a part is dissipated to overcome the resistive characteristics of the respiratory system to generate flow (
). An additional pressure component for the acceleration of the gas depends on the inertia of the respiratory system; it is usually very small and can be disregarded. Hence, the total pressure P produced equals the sum of elastic ( P el ) and resistive ( P res ) components; the former is proportional to V and 1/ C, while the latter is proportional to
and R :
where C (compliance) and R (resistance) are proportionality factors determined by, respectively, the elastic and resistive characteristics of the system.
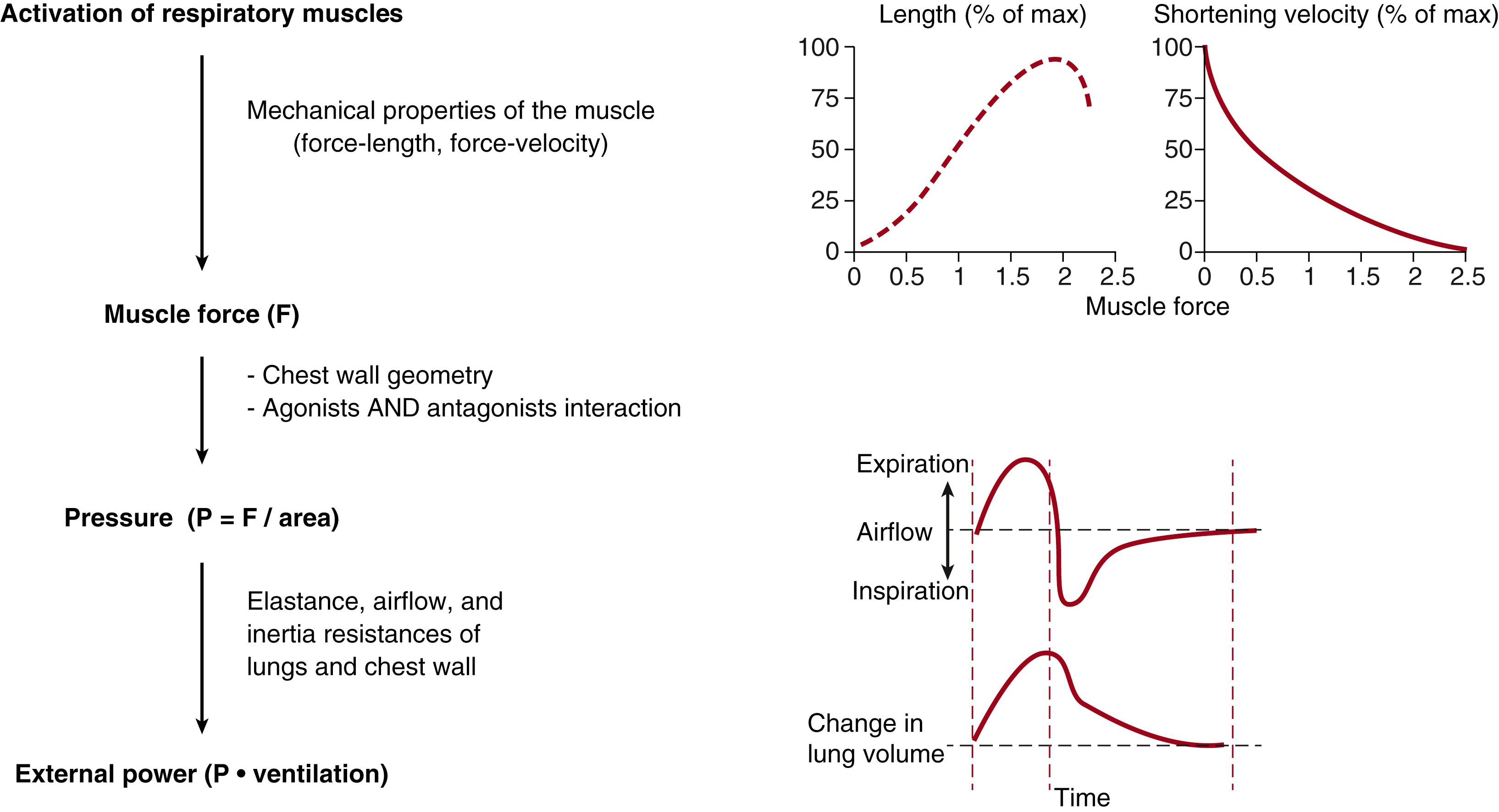
During spontaneous breathing, the total P for inflation is generated by the respiratory muscles. Hence, muscle pressure ( P mus ) equals P , and inflow occurs whenever P mus − P el is greater than 0. During resting breathing, because the tidal volume is entirely above the resting volume of the respiratory system ( V r ), the inspiratory muscles generate P mus and expiration is passive. However, in some conditions, such as certain cases of hyperventilation or during breathing against a positive airway pressure, the expiratory muscles may become active and breathing occurs both above and below V r . In these cases, inspiration originates from the recoil of the respiratory system after expiratory muscle relaxation plus the active contraction of the inspiratory muscles.
During external (mechanical) ventilation, P mus = 0, and the driving pressure is generated by the ventilator, which opposes P el and P res . Whenever P mus = 0, the system is in passive mode; this is the case during lung expansion by a ventilator or in the last portion of expiration during resting breathing. During this phase, the elastic pressure stored during inspiration ( P el ) is the sole driving pressure generating expiratory flow—that is,
.
Whenever P mus differs from 0, the system is in an active mode; of course, this is the case during spontaneous inspiration or when
during voluntary breath holding (in which case P mus = P el ).
Whenever
, Equation 63.1 simplifies to
This condition is defined as static, irrespective of whether P el is offset by muscle activity (e.g., during breath holding) or by external means with P mus = 0 (e.g., relaxation against an artificial occlusion of the airways). In contrast, whenever
differs from 0, the system is in a dynamic condition again, irrespective of whether the respiratory muscles are active (e.g., inflation during spontaneous inspiration) or not (e.g., inflation by a ventilator). In conclusion, the operating modes of the respiratory system can be summarized into four combinations, static or dynamic, depending on the absence or presence of
, each either active or passive, depending on the presence or absence of muscle activity ( Table 63.1 ).
| BTPS | Body temperature, ambient pressure, saturated with water vapor |
| C ( C L , C rs , C w ) | Compliance (of lungs, respiratory system, chest wall), mL/cm H 2 O |
| FRC | Functional residual capacity (end-expiratory volume), mL |
| P | Pressure, cm H 2 O |
| P ao | Pressure at the airway opening, cm H 2 O |
| P el | Elastic pressure (proportional to lung volume), cm H 2 O |
| P es | Esophageal pressure (proportional to pleural pressure), cm H 2 O |
| P mus | Pressure generated by the respiratory muscles, cm H 2 O |
| P res | Resistive pressure (proportional to airflow), cm H 2 O |
| R ( R L , R r s , R w ) | Resistance (of the lungs, respiratory system, chest wall), cm H 2 O/mL/s |
| τ rs | Passive time constant of the respiratory system, s |
| τ rs(exp) | Expiratory time constant of the respiratory system, s |
| V | Volume, mL BTPS |
| V r | Static relaxation volume of the respiratory system, mL |
| V T | Tidal volume, mLBTPS |
| |
Flow, mL BTPS /s |
| Active mode | P mus > 0, respiratory muscles are active |
| Passive mode | P mus = 0, respiratory muscles are relaxed |
| Static condition | . Active: breath holding by muscle contraction above or below V r . Passive: relaxation against closed airways above V r ( P ao > 0), below V r ( P ao < 0), or at V r ( P ao = 0) |
| Dynamic condition | . Active: activation of the respiratory muscles, as during spontaneous breathing. Passive : respiration driven by external means, with respiratory muscles relaxed, as during mechanical ventilation or in the late portion of expiration during resting breathing |
A dynamic condition with changes in V so small that the component V ⋅1/ C in Equation 63.1 is negligible is approached whenever
is very high and V is very small, such as with thermal panting or high-frequency ventilation. During an inspiratory effort against closed airways, because the change in lung volume equals 0 (and therefore
), no external work is performed and the energy of isometric contraction is dissipated entirely as heat.
As defined already, the respiratory system is in a passive mode when P mus = 0. This is the case during paralysis, with the lungs ventilated by external means (e.g., during positive pressure ventilation) or without paralysis after a period of hyperventilation. Hyperventilation lowers the arterial partial pressure of carbon dioxide below the threshold for muscle activation, which is just a few millimeters of mercury below the resting arterial partial pressure of carbon dioxide. During spontaneous breathing, the passive mode occurs when the subject relaxes at lung volumes above the resting position of the respiratory system; in infants, this is the case after an occlusion of the airways at the end of inspiration. The sustained lung inflation activates the airway slowly adapting stretch receptors, which trigger the vagally mediated Hering-Breuer inflation reflex and cause relaxation of the inspiratory muscles. This brief period of artificially provoked muscle relaxation is important in the context of pulmonary function testing in human neonates and is sufficient to evaluate the passive mechanical properties of the respiratory system ( C rs , R rs ) during spontaneous breathing.
Measurements of passive mechanics of the respiratory system are easier to perform during artificial ventilation than during spontaneous breathing because P mus = 0 and the passive conditions are guaranteed. In addition, because it is customary to ventilate the lungs through an endotracheal tube, the infant’s upper airways are bypassed, eliminating an important source of nonlinear mechanical behavior. Therefore the respiratory system will likely perform as a first-order mechanical system, which simplifies the conceptual approach and the analysis of the measurements.
In intubated infants undergoing mechanical ventilation, the pneumotachograph, placed in series between the endotracheal tube and the ventilator, measures
. The
signal is amplified and electronically integrated to obtain the changes in lung volume (V) . The total P needed to inflate the whole respiratory system ( P in Equation 63.1 ) is conveniently measured at the airway opening ( P ao )—for example, at the mouth or at the inlet of the endotracheal tube. From these measurements, C rs and R rs are either separately computed or derived from the equation of motion of the respiratory system (Equation 63.1). Because three (
, V , P ao ) of the five variables are measured, it is possible to derive mathematically the two unknown constants, C rs and R rs . Measurements of C rs and R rs during mechanical ventilation are often plagued by air leaks around the endotracheal tube; a cuffed tube would eliminate the problem, but it is rarely used in routine clinical management. Air leaks can introduce enormous errors in the computation of the volume of air delivered to the lungs and of the parameters related to it. Alternative methods for measurements of changes in lung volume in artificially ventilated infants, such as head-out body plethysmography and respiratory inductance plethysmography, are cumbersome and of little value in the clinical setting. Measurements of R rs as commonly performed (see later) need to take into account that the endotracheal tube resistance is often quite high in comparison with R rs , and its computation can be difficult because the fluid dynamics of small tubes is prone to substantial errors. The monitoring of the inflation pressure at the distal end of the tube, rather than at its proximal end, could eliminate this potential analytical problem.
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here