Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Learning how to interpret medical data will make you a better clinician, researcher, and teacher.
Interpreting data begins by assessing the investigation that produced it; low-quality data with a high risk of bias are of limited value, regardless of how appealing the results may seem.
The presence or absence of a control or comparison group has a profound influence on data interpretation. An uncontrolled study is purely descriptive and cannot assess effectiveness or efficacy.
Statistical tests often make assumptions about the underlying data. Unless these assumptions are met, the results are invalid.
Uncertainty is present in all data because of the inherent variability in biologic systems and in our ability to assess them in a reproducible fashion. Results should be reported with effect sizes and 95% confidence intervals, which incorporate uncertainty by providing a zone of compatibility with the data.
All statistical tests measure error. The P value is the likelihood of a type I error (false-positive conclusion), which occurs if a true null hypothesis is mistakenly rejected. Conversely, a type II error (false-negative conclusion) occurs when a real difference is missed and is related to statistical power and sample size.
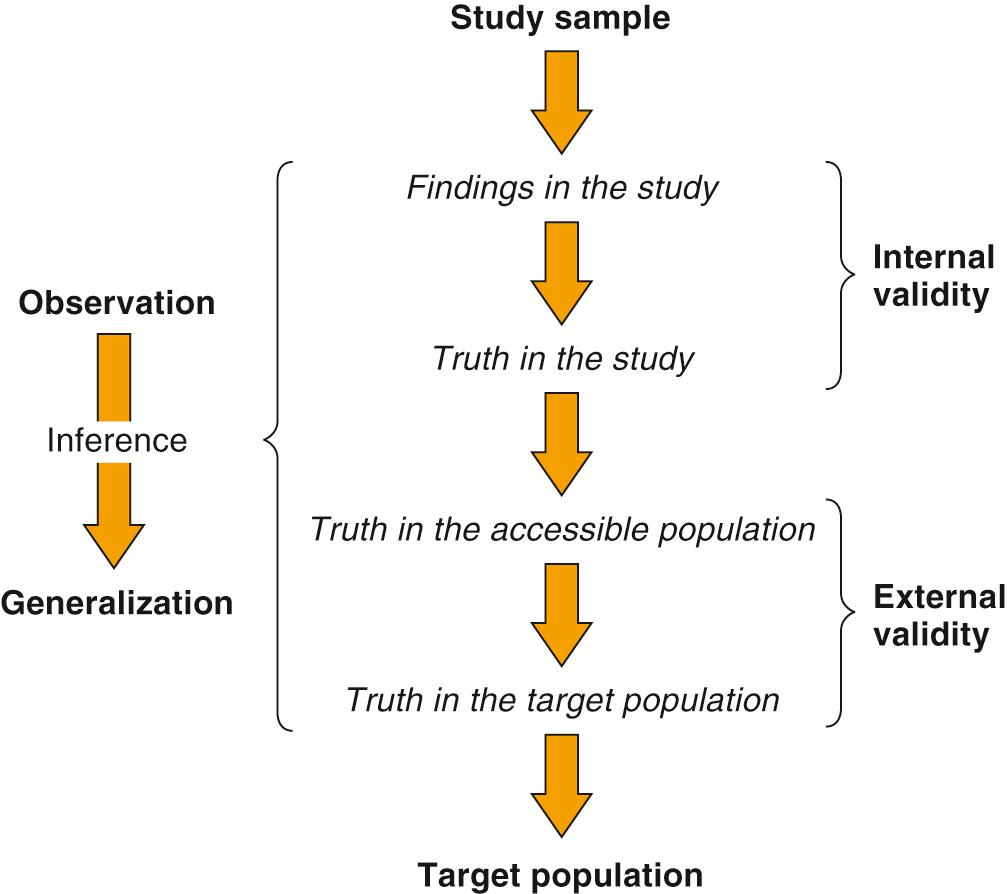
A study has internal validity when the data are analyzed and interpreted properly, but external validity (generalizability) requires that the study sample be representative of the larger population to which it is intended to apply.
Confidence intervals and common sense are needed to balance statistical significance with what is clinically important to patients.
A single study is rarely definitive. Science is a cumulative process that requires a large body of consistent and reproducible evidence before conclusions can be formed.
Effective data interpretation facilitates moving from observations to generalizations with predictable degrees of certainty and uncertainty.
In every chapter of this text, whether it relates to clinical medicine or basic science, the authors draw on their own experience and the experience of others to form valid and generalizable conclusions. Experience yields data, and interpreting data is the heart and soul of the cumulative process called science. Learning how to interpret medical data will make you a better clinician, researcher, and teacher.
Effective data interpretation is a habit: a combination of knowledge, skill, and desire. By applying the seven habits shown in Table 2.1 and further outlined in this chapter, any otolaryngologist—regardless of his or her level of statistical knowledge or lack thereof—can interpret data. Practitioners can also improve their ability to understand and critically appraise the biomedical literature. The numerous tables that accompany the text were designed as stand-alone reminders and often contain keywords with definitions endorsed by the International Epidemiological Association (IEA).
| Habit | Underlying Principles | Keywords |
|---|---|---|
|
All data are not created equal; fancy statistics cannot salvage biased data from a poorly designed and executed study. | Bias, accuracy, research design, internal validity, confounding, causality |
|
Special data require special tests; improper analysis of small samples or data with an asymmetric distribution gives deceptive results. | Measurement scale, frequency distribution, descriptive statistics |
|
All observations have some degree of random error; interpretation requires estimating the associated level of precision or confidence. | Precision, random error, confidence intervals |
|
Uncertainty in observation implies certainty of error; positive results must be qualified by the chance of being wrong, negative results by the chance of having missed a true difference. | Statistical test, type I error, P value, type II error, power |
|
Statistical tests measure error, not importance; an appropriate measure of clinical importance must be checked. | Effect size, statistical significance, clinical importance |
|
Results from one dataset do not necessarily apply to another; findings can be generalized only for a random and representative sample. | Population, sample, selection criteria, external validity |
|
A single study is rarely definitive; data must be interpreted relative to past efforts and by their implications for future efforts. | Research integration, level of evidence, meta-analysis |
This chapter also discusses the practice of data interpretation and includes specific hypothesis tests, sample size determinations, and common statistical deceptions encountered in the otolaryngology literature. You do not have to be a wizard with numbers to understand data; all you need are patience, persistence, and a few good habits that will help settle the dust that follows the clash of statistics with the human mind.
The seven habits that follow are the key to understanding data. They embody fundamental principles of epidemiology and biostatistics developed in a logical and sequential fashion. Table 2.1 gives an overview of the seven habits and their corresponding principles and keywords.
Bias is a four-letter word that is easy to ignore but difficult to avoid. Data collected specifically for research ( Table 2.2 ) are likely to be unbiased—they reflect the true value of the attribute being measured. In contrast, data collected during routine clinical care will vary in quality depending on the specific methodology applied.
| Aspect of Study Design | Effect on Data Interpretation |
|---|---|
| H ow W ere the D ata O riginally C ollected ? | |
| Specifically for research | Interpretation is facilitated by quality data collected according to an a priori protocol. |
| During routine clinical care | Interpretation is limited by consistency, accuracy, availability, and completeness of the source records. |
| Database or data registry | Interpretation is limited by representativeness of the sample and the quality and completeness of data fields. |
| I s the S tudy E xperimental or O bservational ? | |
| Experimental study with conditions under direct control of the investigator | Low potential for systematic error ( bias ); bias can be reduced further by randomization and masking ( blinding ). |
| Observational study without intervention other than to record, classify, analyze | High potential for bias in sample selection, treatment assignment, measurement of exposures, and outcomes. |
| I s T here a C omparison or C ontrol G roup ? | |
| Comparative or controlled study with two or more groups | Permits analytic statements concerning efficacy, effectiveness, and association. |
| No comparison group present | Permits descriptive statements only because of improvements from natural history and placebo effect. |
| W hat I s the D irection of S tudy I nquiry ? | |
| Subjects identified before an outcome or disease; future events recorded | Prospective design measures incidence (new events) and causality (if a comparison group included). |
| Subjects identified after an outcome or disease; past histories examined | Retrospective design measures prevalence (existing events) and causality (if a comparison group is included). |
| Subjects identified at a single time point, regardless of outcome or disease | Cross-sectional design measures prevalence (existing events) and association (if a comparison group is included). |
Experimental studies, such as randomized controlled trials (RCTs), often yield high-quality data because they are performed under carefully controlled conditions. In observational studies, however, the investigator is simply a bystander who records the natural course of health events during clinical care. Although more reflective of “real life” than a contrived experiment, observational studies are more prone to bias. Comparing RCTs with outcomes studies highlights the difference between experimental and observational research ( Table 2.3 ).
| Characteristic | Randomized Controlled Trial | Outcomes Study |
|---|---|---|
| Level of investigator control | Experimental | Observational |
| Treatment allocation | Random assignment | Routine clinical care |
| Patient selection criteria | Restrictive | Broad |
| Typical setting | Hospital or university based | Community based |
| End point definition | Objective health status | Subjective quality of life |
| End point assessment | Masked (blinded) | Unmasked |
| Statistical analysis | Comparison of groups | Multivariate regression |
| Potential for bias | Low | Very high |
| Generalizability | Potentially low | Potentially high |
The presence or absence of a control group has a profound influence on data interpretation. An uncontrolled study, no matter how elegant, is purely descriptive. Case series, which appear frequently in the otolaryngology literature, cannot assess efficacy or effectiveness, but they can convey feasibility, experience, technical details of an intervention, and predictive factors associated with good outcomes or adverse events. The best case series (1) include a consecutive sample of subjects; (2) describe the sample fully and include details of interventions and adjunctive treatments; (3) account for all participants enrolled, including withdrawals and dropouts; and (4) ensure that follow-up duration is adequate to overcome random disease fluctuations.
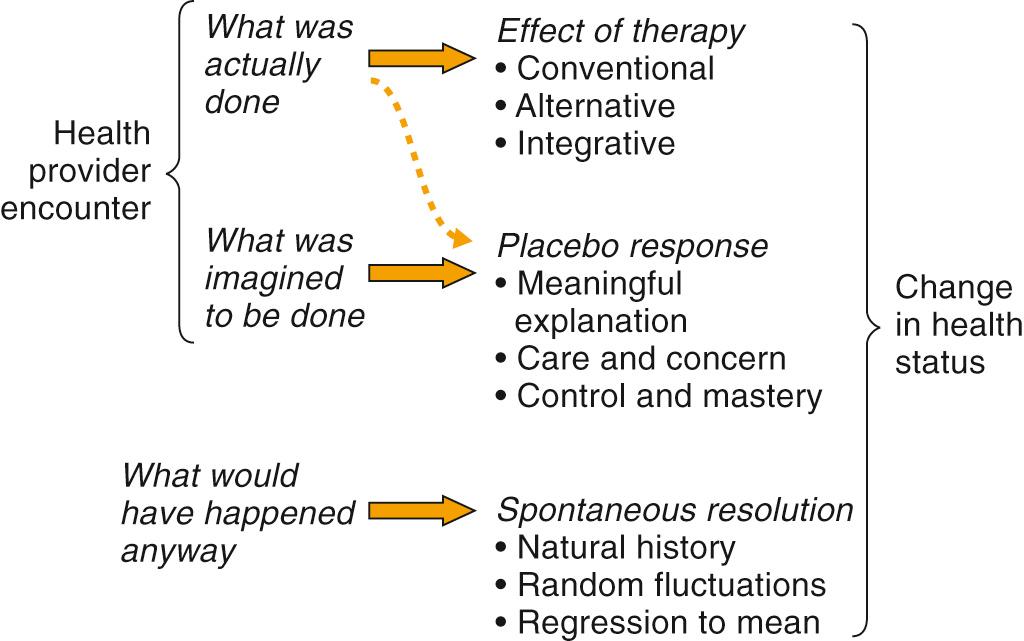
Without a control or comparison group, treatment effects cannot be distinguished from other causes of clinical change ( Table 2.4 ). Some of these causes are seen in Fig. 2.1 , which depicts change in health status after a healing encounter as a complex interaction of three primary factors.
What was actually done . Specific effects of therapy, which include medications, surgery, physical manipulations, and alternative or integrative approaches.
What was imagined to be done . Placebo response, defined as a change in health status resulting from the symbolic significance attributed by the patient (or proxy) to the encounter itself. A placebo response is most likely to occur when the patient receives a meaningful and personalized explanation, feels care and concern expressed by the practitioner, and achieves control and mastery over the illness or believes that the practitioner can control the illness.
What would have happened anyway . Spontaneous resolution, which includes natural history, random fluctuations in disease status, and regression to a mean symptom state.
| Explanation | Definition | Solution |
|---|---|---|
| Bias | Systematic deviation of results or inferences from truth; may be intentional or unintentional | Accurate, protocol-driven data collection |
| Chance | Random variation without apparent relation to other measurements or variables (e.g., luck) | Control or comparison group |
| Natural history | Course of a disease from onset to resolution; may include relapse, remission, and spontaneous recovery | Control or comparison group |
| Regression to the mean | Symptom improvement independent of therapy, as sick patients return to a mean level after seeking care | Control or comparison group |
| Placebo effect | Beneficial effect caused by the expectation that the regimen will have an effect (e.g., power of suggestion) | Control or comparison group with placebo |
| Halo effect | Beneficial effect caused by treatment novelty or by the provider's manner, attention, and caring | Control or comparison group treated similarly |
| Hawthorne effect | Beneficial effect caused by the participant's knowledge of being evaluated and observed in a study | Control or comparison group treated similarly |
| Confounding | Distortion of a measure of the effect of an exposure on an outcome by other prognostic factors or variables that influence the occurrence of the outcome | Randomization or multivariate analysis |
| Allocation (susceptibility) bias | Beneficial effect caused by allocating subjects with less severe disease or better prognosis to the treatment group | Randomization or comorbidity analysis |
| Ascertainment (detection) bias | Favoring the treatment group during outcome analysis (e.g., rounding numbers up for treated subjects and rounding them down for controls) | Masked (blinded) outcome assessment |
The placebo response differs from the traditional definition of placebo as an inactive medical substance. Whereas a placebo can elicit a placebo response, the latter can occur without the former. A placebo response results from the psychologic or symbolic importance attributed by the patient to any nonspecific event in a healing environment. These events include touch, words, gestures, local ambience, and social interactions. Many of these factors are encompassed in the term caring effects , which have been central to medical practice in all cultures throughout history. Caring and placebo effects are so important that they have been deliberately used to achieve positive outcomes in clinical practice.
Questionnaires and quality-of-life surveys are particularly prone to bias (see Table 2.4 ) when response rates are not reported and if the measures have not been formally assessed for reliability, validity, and responsiveness. Unless the authors used a “validated” measure, the results are suspect, but problems may also arise if a validated instrument is used in an inappropriate way. For example, some surveys are developed specifically to compare individuals at a point in time (discriminative surveys) and may not be valid when used to measure change in status within individuals before and after intervention (evaluative surveys). Additional bias may arise in survey research related to sampling the population, administering the questionnaire, and managing the resultant data.
When data from a comparison or control group are available, inferential statistics may be used to test hypotheses and measure associations. Causality may also be assessed when the study has a time-span component, either retrospective or prospective (see Table 2.2 ). Prospective studies measure incidence (new events), whereas retrospective studies measure prevalence (existing events). Unlike time-span studies, cross-sectional inquiries measure association, not causality. Examples include surveys, screening programs, and evaluation of diagnostic tests. Study design, in general, can greatly impact the ability of clinicians and others to use research to assess treatment claims and to make informed health choices.
Another clue to data quality is study type, but this cannot replace the four questions in Table 2.2 . Note the variability in data quality for the study types listed in Table 2.5 , particularly the observational designs. Randomization balances baseline prognostic (confounding) factors, both known and unknown, among groups; this includes factors such as severity of illness and the presence of comorbid conditions. Because these factors also influence a clinician's decision to offer treatment, nonrandomized studies are prone to allocation (susceptibility) bias (see Table 2.4 ) and false-positive results. For example, when the survival of surgically treated cancer patients is compared with the survival of nonsurgical controls (e.g., patients treated with radiation or chemotherapy) without randomization, the surgical group will generally have a more favorable prognosis independent of therapy because the customary criteria for operability—special anatomic conditions and no major comorbidity—also predispose to favorable results.
| Study Type | How Were the Data Originally Collected? | Was a Control or Comparison Group Included? | What Is the Direction of the Study Inquiry? |
|---|---|---|---|
| E xperimental S tudies | |||
| Basic science study | Research | Yes or no | Prospective or cross-sectional |
| Clinical trial | Research | Yes or no | Prospective or cross-sectional |
| Randomized trial | Research | Yes | Prospective |
| O bservational S tudies | |||
| Cohort study | Clinical care or research | Yes or no | Prospective |
| Historical cohort study a | Clinical care | Yes | Prospective |
| Outcomes research | Clinical care or research | Yes or no | Prospective |
| Case-control study | Clinical care | Yes | Retrospective |
| Case series | Clinical care | Yes or no | Retrospective or prospective |
| Survey study | Clinical care or research | Yes or no | Cross-sectional |
| Diagnostic test study | Clinical care or research | Yes or no | Cross-sectional |
a Also called a retrospective cohort study or nonconcurrent cohort study.
The relationship between data quality and interpretation is illustrated in Table 2.6 using hypothetical studies to determine whether tonsillectomy causes baldness. Note how a case series (examples 1 and 2) can have either a prospective or retrospective direction of inquiry, depending on how subjects are identified; contrary to common usage, all cases series are not “retrospective reviews.” Only the controlled studies (examples 3 through 7) can measure associations, and only the controlled studies with a time-span component (examples 4 through 7) can assess causality. The nonrandomized studies (examples 3 through 6), however, require adjustment for potential confounding variables—baseline prognostic factors that may be associated with both the intervention (tonsillectomy) and the outcome (baldness) and may therefore distort results. As noted previously, adequate randomization helps balance prognostic factors among groups, thereby reducing confounding.
| Study Design a | Study Execution | Interpretation |
|---|---|---|
|
A group of bald subjects are questioned as to whether or not they had a tonsillectomy. | Measures prevalence of tonsillectomy in bald subjects; cannot assess association or causality |
|
A group of subjects who had or who are about to have tonsillectomy are examined later for baldness. | Measures incidence of baldness after tonsillectomy; cannot assess association or causality |
|
A group of subjects are examined for baldness and for presence or absence of tonsils at the same time. | Measures prevalence of baldness and tonsillectomy and their association; cannot assess causality |
|
A group of bald subjects and a group of nonbald subjects are questioned about prior tonsillectomy. | Measures prevalence of baldness and association with tonsillectomy; limited ability to assess causality |
|
A group of subjects who had prior tonsillectomy and a comparison group with intact tonsils are examined later for baldness. | Measures incidence of baldness and association with tonsillectomy; can assess causality when adjusted for confounding variables |
|
A group of nonbald subjects about to have tonsillectomy and a nonbald comparison group with intact tonsils are examined later for baldness. | Measures incidence of baldness and association with tonsillectomy; can assess causality when adjusted for confounding variables |
|
A group of nonbald subjects with intact tonsils are randomly assigned to tonsillectomy or observation and are examined later for baldness. | Measures incidence of baldness and association with tonsillectomy; can assess causality despite baseline confounding variables |
a Studies are listed in order of increasing ability to establish causal relationship.
Statistical tests often make assumptions about the underlying data. Unless these assumptions are met, the test will be invalid. Describing before you analyze avoids trying to unlock the mysteries of square data with a round key.
Describing data begins by defining the measurement scale that best suits the observations. Categorical (qualitative) observations fall into one or more categories and include dichotomous, nominal, and ordinal scales ( Table 2.7 ). Numeric (quantitative) observations are measured on a continuous scale and are further classified by the underlying frequency distribution , a plot of observed values versus the frequency of each value. Numeric data with a symmetric (normal) distribution are symmetrically placed around a central crest or trough (bell-shaped curve). Numeric data with an asymmetric distribution are skewed (shifted) to one side of the center, have a sloping “exponential” shape that resembles a forward or backward J , or contain some unusually high or low outlier values.
| Scale | Definition | Examples |
|---|---|---|
| Dichotomous | Classification into either of two mutually exclusive categories | Breastfeeding (yes/no), sex (male/female) |
| Nominal | Classification into unordered qualitative categories | Race, religion, country of origin |
| Ordinal | Classification into ordered qualitative categories but with no natural (numeric) distance between their possible values | Hearing loss (none, mild, moderate), patient satisfaction (low, medium, high), age group |
| Numeric | Measurements with a continuous scale or a large number of discrete, ordered values | Temperature, age in years, hearing level in decibels |
| Numeric (censored) | Measurements on subjects lost to follow-up or in whom a specified event has not yet occurred at the end of a study | Survival rate, recurrence rate, or any time-to-event outcome in a prospective study |
Depending on the measurement scale, data may be summarized using one or more of the descriptive statistics given in Table 2.8 . Note that when summarizing numeric data, the descriptive method varies according to the underlying distribution. Numeric data with a symmetric distribution are best summarized with the mean and standard deviation (SD) because 68% of the observations fall within the mean ± 1 SD and 95% fall within the mean ± 2 SD. In contrast, asymmetric numeric data are best summarized with the median, because even a single outlier can strongly influence the mean. If a series of five patients are followed after sinus surgery for 10, 12, 15, 16, and 48 months, the mean duration of follow-up is 20 months, but the median is only 15 months. In this case, a single outlier, 48 months, distorts the mean.
| Descriptive Measure | Definition | Application |
|---|---|---|
| C entral T endency | ||
| Mean | Arithmetic average | Numeric data that are symmetric |
| Median | Middle observation; half the values are smaller, and half are larger | Ordinal data; numeric data with an asymmetric distribution |
| Mode | Most frequent value | Nominal data; bimodal distribution |
| D ispersion | ||
| Range | Largest value minus smallest value | Emphasizes extreme values |
| Standard deviation | Spread of data about their mean | Numeric data that are symmetric |
| Percentile | Percentage of values equal to or below that number | Ordinal data; numeric data with an asymmetric distribution |
| Interquartile range | Difference between the twenty-fifth and seventy-fifth percentiles | Ordinal data; numeric data with an asymmetric distribution |
| O utcome | ||
| Survival rate | Proportion of subjects surviving, or with some other outcome, after a time interval (e.g., 1 year, 5 years) | Numeric (censored) data in a prospective study; can be overall, cause specific, or progression free |
| Odds ratio | Odds of a disease or outcome in subjects; risk factor divided by odds in controls | Dichotomous data in a retrospective or prospective controlled study |
| Relative risk | Incidence of a disease or outcome in subjects; risk factor divided by incidence in controls | Dichotomous data in a prospective controlled study |
| Rate difference a | Event rate in treatment group minus event rate in control group | Compares success or failure rates in clinical trial groups |
| Correlation coefficient | Degree to which two variables have a linear relationship | Numeric or ordinal data |
Although the mean is appropriate only for numeric data with a symmetric distribution, it is often applied regardless of the underlying symmetry. An easy way to determine whether the mean or median is appropriate for numeric data is to calculate both; if they differ significantly, the median should be used. Another way is to examine the SD; when it is very large (e.g., larger than the mean value with which it is associated), the data often have an asymmetric distribution and should be described by the median and interquartile range. When in doubt, the median should always be used over the mean.
A special form of numeric data is called censored (see Table 2.7 ). Data are censored when three conditions apply: (1) the direction of study inquiry is prospective; (2) the outcome of interest is time related; and (3) some subjects die, are lost, or have not yet had the outcome of interest when the study ends. Interpreting censored data is called survival, or time-to-event, analysis because of its use in cancer studies, in which survival is the outcome of interest. Survival analysis permits full use of censored observations (e.g., patients with <1 year of follow-up) by including them in the analysis up to the time the censoring occurred. Results of cancer studies are often reported with Kaplan-Meier curves , which may describe overall survival, disease-free survival, disease-specific survival, or progression-free survival. Survival data at the far right of the curves should be interpreted cautiously because fewer patients remain, which yields less precise estimates.
A survival curve starts with 100% of the study sample alive and shows the percentage still surviving at successive times for as long as information is available. The resulting hazard function yields a continuous curve that shows how the risk of having the event or outcome (e.g., the hazard rate) changes over time. Survival analysis may also be applied to any situation where time-to-event is important, not just to absence of mortality. For example, the 3-, 5-, or 10-year rates for cholesteatoma recurrence or the future “survival” of tonsils (i.e., no need for tonsillectomy) could be estimated in a cohort of children after adenoidectomy alone. Similarly, survival analysis could be used to estimate the time to occlusion or extrusion of tympanostomy tubes.
Several statistical methods are available for analyzing survival data. The Kaplan-Meier (product-limit) method records events by exact dates and is suitable for small and large samples. Conversely, the life-table (actuarial) method records events by time interval (e.g., every month, every year) and is most commonly used for large samples in epidemiologic studies. When censored data need adjustment for multiple prognostic or confounding variables, which might independently influence time-to-event, the Cox proportional hazards model can calculate hazard ratios for all variables (prognostic and confounding).
The odds ratio, relative risk, and rate difference (see Table 2.8 ) are useful ways of comparing two groups of dichotomous (binary) data. A retrospective (case-control) study of tonsillectomy and baldness might report an odds ratio of 1.6, indicating that bald subjects were 1.6 times more likely to have had tonsillectomy than were nonbald controls. In contrast, a prospective study would report results using relative risk. A relative risk of 1.6 means that baldness was 1.6 times more likely to develop in tonsillectomy subjects than in nonsurgical controls. When interpreting binary data, readers should note that the odds ratio and relative risk will be similar if the event rate is small, but for common events they can diverge widely. Finally, a rate difference of 30% in a prospective trial or experiment reflects the increase in baldness caused by tonsillectomy above and beyond what occurred in controls. No association exists between groups when the rate difference equals zero or the odds ratio or relative risk equals one (unity).
Two groups of ordinal or numeric data are compared with a correlation coefficient (see Table 2.8 ). A coefficient ( r ) from 0 to 0.25 indicates little or no relationship, from 0.25 to 0.49 a fair relationship, from 0.50 to 0.74 a moderate to good relationship, and greater than 0.75 a good to excellent relationship. A perfect linear relationship would yield a coefficient of 1.00. When one variable varies directly with the other, the coefficient is positive; a negative coefficient implies an inverse association. Sometimes the correlation coefficient is squared ( r 2 ) to form the coefficient of determination, which estimates the percentage of variability in one measure that is predicted by the other.
Uncertainty is present in all data because of the inherent variability in biologic systems, and it is present in our ability to assess data in a reproducible fashion. If we were to measure hearing in 20 healthy volunteers on five different days, it would be very unlikely for us to get the same mean result each time; this is because audiometry has a variable behavioral component that depends on the subject's response to a stimulus and the examiner's perception of that response. Similarly, if hearing were to be measured in five groups of 20 healthy volunteers each, it would be very unlikely for us to get the same mean hearing level in each group; again, it would be unlikely because of variations among individuals. A range of similar results would be obtained, but rarely would the exact same result be obtained on repetitive trials.
Uncertainty must be dealt with when interpreting data unless the results are meant to apply only to the particular group of patients, animals, cell cultures, and DNA strands in which the observations were initially made. Recognizing this uncertainty, each of the descriptive measures in Table 2.8 is called a point estimate that is specific to the data that generated it. In medicine, however, the clinician seeks to pass from observations to generalizations and from point estimates to data applicable to other populations. When this process occurs with calculated degrees of uncertainty, it is called inference .
The following is a brief example of clinical inference. After treating five vertiginous patients with vitamin C, you remark to a colleague that four had excellent relief of their vertigo. She asks, “How confident are you of your results?”
“Quite confident,” you reply. “There were five patients, four got better, and that's 80%.”
“Maybe I wasn't clear,” she interjects. “How confident are you that 80% of vertiginous patients you see in the next few weeks will respond favorably, or that 80% of similar patients in my practice will do well with vitamin C? In other words, can you infer anything about the real effect of vitamin C on vertigo from only five patients?”
Hesitatingly you retort, “I'm pretty confident about that number, 80%, but maybe I’ll have to see a few more patients to be sure.”
The real issue, of course, is that a sample of only five patients offers low precision (repeatability). How likely is it that the same results would be found if five new patients were studied? Actually, it can be stated with 95% confidence that four out of five successes in a single trial is consistent with a range of results from 28% to 99% in future trials. This 95% confidence interval (CI) reveals the range of values considered plausible for the population and provides a zone of compatibility with the data. All point estimates of effect size should ideally be accompanied by a 95% CI, yet this occurs infrequently in the otolaryngology literature, and when it does the authors rarely include an interpretation.
Precision may be increased, or uncertainty may be decreased, by (1) using a more reproducible measure, (2) increasing the number of observations (sample size), or (3) decreasing the variability among the observations. The most common method is to increase the sample size, because the variability inherent in the subjects studied can rarely be reduced. Even a huge sample of perhaps 50 000 subjects still has some degree of uncertainty, but the 95% CI will be quite small. Realizing that uncertainty can never completely be avoided, statistics are used to estimate precision. Thus, when data are described using the summary measures listed in Table 2.8 , a corresponding 95% CI should accompany each point estimate.
Precision differs from accuracy. Precision relates to random error and measures repeatability; accuracy relates to systematic error (bias) and measures nearness to the truth. A precise otologist may always perform a superb mastoidectomy, but an accurate otologist performs it on the correct ear. A precise surgeon cuts on the exact center of the line, but an accurate surgeon first checks the line to be sure its placement is correct. Succinctly put, precision is doing things right, and accuracy is doing the right thing. Precise data include a large enough sample of carefully measured observations to yield repeatable estimates; accurate data are measured in an unbiased manner and reflect what is truly purported to be measured. When we interpret data, we must estimate both precision and accuracy.
To summarize habits 1, 2, and 3: “Check quality before quantity” determines whether or not the data are worth interpreting (habit 1). Assuming they are, “describe before you analyze,” and summarize the data using appropriate measures of central tendency, dispersion, and outcome for the particular measurement scales involved (habit 2). Next, “accept the uncertainty of all data” as noted in habit 3, and qualify the point estimates in habit 2 with 95% CIs to measure precision. When precision is low (e.g., the CI is wide), proceed with caution. Otherwise, proceed with habits 4, 5, and 6, which deal with errors and inference.
To err is human—and statistical. When comparing two or more groups of uncertain data, errors in inference are inevitable. If it can be concluded that the groups are different, they may actually be equivalent. If the conclusion is that they are the same, a true difference may have been missed. Data interpretation is an exercise in modesty, not pretense—any conclusion we reach may be wrong. The ignorant data analyst ignores the possibility of error; the savvy analyst estimates this possibility by using the right statistical test.
Now that we have stated the problem in English, let us restate it in thoroughly confusing statistical jargon ( Table 2.9 ). We begin with some testable hypotheses about the groups we are studying, such as “Gibberish levels in group A differ from those in group B.” Rather than keep it simple, we now invert this to form a null hypothesis: “Gibberish levels in group A are equal to those in group B.” Next we fire up our personal computer, enter the gibberish levels for the subjects in both groups, choose an appropriate statistical test, and wait for the omnipotent P value to emerge.
| Term | Definition |
|---|---|
| Central tendency | A supposition arrived at from observation or reflection that leads to predictions that can be tested and refuted |
| Null hypothesis | Results observed in a study, experiment, or test that are no different from what might have occurred because of chance alone |
| Statistical test | Procedure used to reject or accept a null hypothesis; statistical tests may be parametric, nonparametric (distribution free), or exact |
| Type I (α) error | Wrongly rejecting a null hypothesis (false-positive error); declaring that a difference exists, when in fact it does not |
| P value | Probability of making a type I error; P < .05 indicates a statistically significant result that is unlikely to have been caused by chance |
| Confidence interval | A zone of compatibility with the data, which also indicates a range of values considered plausible for the population from which the study sample was selected |
| Type II (β) error | Failing to reject a false null hypothesis (false-negative error); declaring that a difference does not exist, when in fact it does |
| Power | Probability that the null hypothesis will be rejected if it is indeed false; mathematically, power is 1.00 minus type II error |
The P value gives the probability of making a type I error: rejection of a true null hypothesis. In other words, if P = .10, there is a 10% chance of being wrong when we declare that group A differs from group B based on the observed data. Alternatively, there is a 10% probability that the difference in gibberish levels is explainable by random error—we cannot be certain that uncertainty is not the cause. In medicine, P < .05 is generally considered low enough to safely reject the null hypothesis. Conversely, when P > .05, the null hypothesis of equivalent gibberish levels is accepted. Nonetheless, one might be making a type II error by accepting a false null hypothesis. Rather than state the probability of a type II error directly, it is stated indirectly by specifying power (see Table 2.9 ).
Moving from principles to practice, two hypothetical studies are presented. The first is an observational prospective study to determine whether tonsillectomy causes baldness: 20 patients who underwent tonsillectomy and 20 controls are examined 40 years later, and the incidence of baldness is compared. The second study will use the same groups but will determine whether tonsillectomy causes hearing loss. This allows exploration of statistical error from the perspective of a dichotomous outcome (bald vs. nonbald) and a numeric outcome (hearing level in decibels).
Suppose that baldness develops in 80% of tonsillectomy patients (16/20) but in only 50% of controls (10/20). If we infer, based on these results in 40 specific patients, that tonsillectomy predisposes to baldness in general, what is the probability of being wrong (i.e., a type I error)? Because P = .10 (Fisher exact test), a 10% chance of type I error exists, so we should be reluctant to associate tonsillectomy with baldness based on this single study; the strength of the evidence against the null hypothesis is simply too much to ignore.
Intuitively, however, a rate difference of 30% (e.g., 80% minus 50%) seems significant; so what is the chance of being wrong when we conclude that it is not (i.e., a type II error)? The probability of a type II error (false-negative result) is actually 48%, the same as saying 52% power, which means we may indeed be wrong in accepting the null hypothesis; therefore, a larger study is needed before any definitive conclusions can be drawn.
Intrigued by the initial findings, we repeat the tonsillectomy study with twice as many patients in each group. Suppose that baldness again develops in 80% of tonsillectomy patients (32/40) but in only 50% of controls (20/40). The rate difference is still 30%, but now P = .01 (Fisher exact test). The conclusion is that tonsillectomy is associated with baldness, with only a 1% chance of making a type I error (false-positive result). By increasing the number of subjects studied, the precision is increased to a level that could move from observation to generalization with a tolerable level of uncertainty. Similarly, the strength of the evidence against the null hypothesis is now much higher.
Returning to the earlier study of 20 tonsillectomy patients and 20 controls, the hearing levels for the groups are 25 ± 9 decibels (dB) and 20 ± 9 dB, respectively (mean value ± SD). What is the chance of being wrong if we infer that posttonsillectomy patients have hearing levels 5 dB lower than controls? Because P = .09 ( t test), the probability of a type I error is 9%. If, however, we conclude that no true difference exists between the groups, the chance of making a type II error is 58%. Thus, little can be said about the impact of tonsillectomy on hearing based on this study, because power is only 42%. In general, studies with “negative” findings should be interpreted by power, not P values.
When making inferences about numeric data, precision may be increased by studying more subjects or by studying subjects with less variability in their responses. For example, suppose again that there are 20 tonsillectomy patients and 20 controls, but this time the hearing levels are 25 ± 3 dB and 20 ± 3 dB. Although the difference remains 5 dB, the SD is only 3 for this study, compared with 9 in the preceding example. What effect does this reduced variability have on the ability to make inferences? The P value is now less than .001 ( t test), indicating less than a 1 : 1000 probability of a type I error if we conclude that the hearing levels truly differ.
All statistical tests measure error. Choosing the right test for a particular situation ( Tables 2.10 and 2.11 ) is determined by (1) whether the observations come from independent or related samples, (2) whether the purpose is to compare groups or to associate an outcome with one or more predictor variables, and (3) the measurement scale of the variables. When associating an outcome with predictor variables in an observational study, a propensity score can be incorporated into the analysis to reduce bias from baseline factors that might influence choice of treatment (e.g., age, illness severity, prior exposures).
| Situation | Parametric Test | Nonparametric Test |
|---|---|---|
| C omparing T wo G roups of D ata | ||
| Numeric scale | t Test | Mann-Whitney U , a median |
| Numeric (censored) scale | Mantel-Haenszel life table | Log rank, Mantel-Cox |
| Ordinal scale | — | Mann-Whitney U , a median test; chi-squared test for trend |
| Nominal scale | — | Chi-squared, log-likelihood ratio |
| Dichotomous scale | — | Chi-squared, Fisher exact, odds ratio, relative risk |
| C omparing T hree or M ore G roups of D ata | ||
| Numeric scale | One-way ANOVA | Kruskal-Wallis ANOVA |
| Ordinal scale | — | Kruskal-Wallis ANOVA; chi-squared test for trend |
| Dichotomous or nominal scale | — | Chi-squared, log-likelihood ratio |
| A ssociating an outcome W ith P redictor V ariables | ||
| Numeric outcome, one predictor | Pearson correlation | Spearman rank correlation |
| Numeric outcome, two or more predictor variables | Multiple linear regression, two-way ANOVA | — |
| Numeric (censored) outcome | Proportional hazards (Cox) regression | — |
| Dichotomous outcome | Discriminant analysis | Multiple logistic regression |
| Nominal or ordinal outcome | Discriminant analysis | Log-linear model |
a The Mann-Whitney U test is equivalent to the Wilcoxon rank-sum test.
| Situation | Parametric Test | Nonparametric Test |
|---|---|---|
| C omparing T wo G roups of D ata | ||
| Dichotomous scale | — | McNemar |
| Ordinal scale | — | Sign, Wilcoxon signed rank |
| Numeric scale | Paired t test | Sign, Wilcoxon signed rank |
| C omparing T hree or M ore G roups of D ata | ||
| Dichotomous scale | — | Cochran Q, Mantel-Haenszel chi-squared |
| Ordinal scale | — | Friedman ANOVA |
| Numeric scale | Repeated measures ANOVA | Friedman ANOVA |
Two events are independent if the occurrence of one is in no way predictable from the occurrence of the other. A common example of independent samples is two or more parallel (concurrent) groups in a clinical trial or observational study. Conversely, related samples include paired organ studies, subjects matched by age and sex, and repeated measures on the same subjects (e.g., before and after treatment). Longitudinal studies may include repeated measurements over time, which makes them challenging to analyze unless mixed models are used to explicitly account for the correlations between repeated measures within each patient. Measurement scales were discussed previously, but the issue of frequency distribution deserves reemphasis. The tests in Tables 2.10 and 2.11 labeled as “parametric” assume an underlying symmetric distribution for data. If the data are sparse, asymmetric, or plagued with outliers, a “nonparametric” test must be used.
Using the wrong statistical test to estimate error invalidates results. For example, suppose intelligence quotient (IQ) is measured in 20 subjects before and after tonsillectomy, and the mean IQ increases from 125 to 128. For this three-point increase, P = .29 ( t test, independent samples) suggests a high probability (29%) of reaching a false-positive conclusion. However, the observations in this example are related before and after IQ tests in the same subjects. What is really of interest is the mean change in IQ for each subject (related samples), not how the mean IQ of all subjects before surgery compares with the mean IQ of all subjects postoperatively (independent samples). When the proper statistical test is used ( t test, paired samples), P = .05 suggests a true association. Related (matched) samples are common in biomedical studies and should never be analyzed as though they were independent.
Results are statistically significant when the probability of a type I error is low enough ( P < .05) to safely reject the null hypothesis. If the statistical test compared two groups, we conclude that the groups differ. If the statistical test compared three or more groups, we conclude that global differences exist among them. If the statistical test related predictor and outcome variables (regression analysis), we conclude that the predictor variables explain more variation in the outcome than would be expected by chance alone. These generalizations apply to all the statistical tests in Tables 2.10 and 2.11 .
The next logical questions after “Is there a difference?” (statistical significance) is “How big a difference is there?” (effect size) and “Is this difference important to patients?” (minimal clinically important difference, or MCID). Unfortunately, most data interpretation stops with the P value, and the other questions are never asked. For example, a clinical trial of nonsevere acute otitis media found amoxicillin superior to placebo as an initial treatment ( P = .009). Before we agree with the author's recommendation for routine amoxicillin therapy, let us look more closely at the effect size. Initial treatment success occurred in 96% of amoxicillin-treated children versus 92% of controls, yielding a 4% rate difference that favored drug therapy. Alternatively, 25 subjects (100/4) must be treated (number needed to treat) with amoxicillin to increase the success rate by one subject over what would occur from placebo alone. Is this clinically important to patients? Possibly not, especially when we balance the small benefits against the possible adverse events related to antibiotic therapy.
Statistically significant results must be accompanied by a measure of effect size that reflects the magnitude of difference between groups. Otherwise, findings with minimal clinical importance may become statistically significant when a large number of subjects are studied. In the above example, the 4% difference in success rates was highly statistically significant, because more than 1000 episodes of otitis media contributed to this finding. Large numbers provide high precision (repeatability), which in turn reduces the likelihood of error. The final result, however, is a hypnotically tiny P value, which may reflect a clinical difference of trivial importance.
When comparing groups, common measures of effect size include the odds ratio, relative risk, and rate difference (see Table 2.8 ). For example, in the hypothetical study of tonsillectomy and baldness noted earlier, the rate difference was 30% ( P = .01) with a 95% CI of 10% to 50%. Therefore, we can be 95% confident that tonsillectomy increases the rate of baldness between 10% and 50%, with only a 1% chance of a type I error (false-positive). Alternatively, results could be expressed in terms of relative risk. For the tonsillectomy study , relative risk is 1.6 (the incidence of baldness was 1.6 times higher after surgery) with a 95% CI of 1.1 to 2.3.
Effect size is measured by the correlation coefficient ( r ) when an outcome variable is associated with one or more predictor variables in a regression analysis (see Table 2.10 ). Suppose that a study of thyroid surgery reports that shoe size had a statistically significant association with intraoperative blood loss (multiple linear regression, P = .04, r = .10). A correlation of only .10 implies little or no relationship (see habit 2), and an r 2 of .01 means that only 1% of the variance in survival is explainable by shoe size. Who cares if the results are “significant” when the effect size is clinically irrelevant, not to mention nonsensical? Besides, when P = .04, there is a 4% chance of being wrong when the null hypothesis is rejected, which may in fact be the case here. A nonsensical result should prompt a search for confounding factors that may not have been included in the regression, such as tumor-node-metastasis (TNM) stage, comorbid conditions, or duration of surgery.
Confidence intervals are more appropriate measures of clinical importance than are P values, because CIs reflect both magnitude and precision. When a study reports “significant” results, the lower limit of the 95% CI should be scrutinized; a value of minimal clinical importance suggests low precision (inadequate sample size). When a study reports “nonsignificant” results, the upper limit of the 95% CI should be scrutinized; a value indicating a potentially important clinical effect suggests low statistical power (false-negative finding). Ideally, the P value, effect size, and 95% CI for the effect size should all be reported to allow proper interpretation of study results.
When we interpret medical data, we ultimately seek to make inferences about some target population based on results in a smaller sample ( Table 2.12 ). Rarely is it possible to study every patient, medical record, DNA strand, or fruit fly with the condition of interest; nor is it necessary—inferential statistics let us generalize from the few to the many, provided that the few studied are a random and representative sample of the many. However, random and representative samples rarely arise through divine providence; therefore, we must seek the sample source before generalizing the interpretation of the data beyond the confines of the study that produced it.
| Term | Definition |
|---|---|
| Target population | Entire collection of items, subjects, patients, and observations about which inferences are made; defined by the selection criteria (inclusion and exclusion criteria) for the study |
| Accessible population | Subset of the target population accessible for study, generally because of geographic or temporal considerations |
| Study sample | Subset of the accessible population chosen for study |
| Sampling method | Process of choosing a sample from a larger population; the method may be random or nonrandom, representative or nonrepresentative |
| Selection bias | Error caused by systematic differences between a study sample and target population; examples include studies on volunteers and those conducted in clinics or tertiary care settings |
| Sample-size determination | Process of deciding, before a study begins, how many subjects should be studied based on the incidence or prevalence of the condition under study, anticipated differences between groups, the power desired, and the allowable level of type I error |
| Internal study validity | Degree to which conclusions drawn from a study are valid for the study sample; results from proper study design, unbiased measurements, and sound statistical analysis |
| External study validity (generalizability) | Degree to which conclusions drawn from a study are valid for a target population (beyond the subjects in the study); results from representative sampling and appropriate selection criteria |
As an example of sampling, consider a new antibiotic touted as superior to an established standard for treating acute otitis media. When you review the data on which this statement is based, you learn that the study end point was bacteriologic efficacy—the ability to sterilize the middle ear after treatment. Furthermore, the only patients included in the study were those whose initial tympanocentesis revealed an organism with in vitro sensitivity to the new antibiotic; patients with no growth or resistant bacteria were excluded. Can you apply these results to your clinical practice? Most likely not, because you probably do not limit your practice to patients with antibiotic-susceptible bacteria. In other words, the sample of patients included in the study is not representative of the target population in your practice.
A statistical test is valid only when the study sample is random and representative. Unfortunately, these assumptions are frequently violated or overlooked. A random sample is necessary, because most statistical tests are based on probability theory—playing the odds. The odds apply only if the deck is not stacked and the dice are not rigged; that is, all members of the target population have an equal chance of being sampled for study. Investigators, however, typically have access to only a small subset of the target population because of geographic or temporal constraints. When they choose an even smaller subset of this accessible population to study, the method of choosing (sampling method) affects the ability to make inferences about the original target population.
Of the sampling methods listed in Table 2.13 , only a random sample is theoretically suitable for statistical analysis. Nonetheless, a consecutive or systematic sample offers a relatively good approximation and provides data of sufficient quality for most statistical tests. The worst sampling method occurs when subjects are chosen based on convenience or according to subjective judgments about eligibility. Applying statistical tests to the resulting convenience (grab) sample is the equivalent of asking a professional card counter to help you win a blackjack game when the deck is stacked and cards are missing—all bets are off, because probability theory will not apply. A brute force sample of the entire population is also unsatisfactory, because lost, missing, or incomplete units tend to differ systematically from those that are readily accessible.
| Method | How It Is Performed | Comments |
|---|---|---|
| Brute force sample | All units of study accessible to the researchers are included: charts, patients, laboratory animals, and journal articles. | Time consuming and unsophisticated; bias prone, because missing units are seldom randomly distributed. |
| Convenience (grab) sample | Units are selected on the basis of accessibility, convenience, or by subjective judgments about eligibility. | Assume this method when none is specified; study results cannot be generalized because of selection bias. |
| Consecutive sample | Every unit is included over a specified time interval, or until a specified number is reached; the interval should be long enough to include seasonal or other temporal variations relevant to the research question. | Volunteerism and other selection biases can be minimized but requires judgment when generalizing to a target population. |
| Systematic sample | Units are selected using some simple, systematic rule, such as first letter of last name, date of birth, or day of the week. | Less biased than a grab sample, but problems may still occur because of unequal selection probabilities. |
| Random sample | Units are assigned numbers then selected at random until a desired sample size is attained; most common use is in clinical research to select a representative subset from a larger population. | Best method; bias is minimized, because all units have a known (and equal) probability of selection; data can be stratified based on subgroups in the population. |
| Cluster sample | Sample of natural groupings, or clusters, of units in a population is random (e.g., hospitals in a region, city blocks or zip codes, different office sites). | Helps create a manageable sample size, but the clusters are often homogeneous for the variables of interest. |
“Seek the sample source” means that we must identify the sampling method and selection criteria (inclusion and exclusion criteria) that were applied to the target population to obtain the study sample. When the process appears sound, we can conclude that the results are generalizable and externally valid (see Table 2.12 and Fig. 2.2 ). If the process appears flawed, we cannot interpret or extrapolate the results beyond the confines of the study sample.
Sometimes a study is internally valid, but the results may not be generalizable. Paradise and colleagues concluded that prompt versus delayed insertion of tympanostomy tubes for persistent otitis media does not affect child development. Although the study was meticulously designed and analyzed (internally valid), the participants had mostly unilateral (63%) or discontinuous (67%) otitis media with effusion; bilateral continuous effusions were uncommon (18%). Moreover, children with syndromes, developmental delays, or other comorbidities were excluded. Whereas no benefits were seen in the healthy children studied, the results are not generalizable to the more typical population of children who receive tubes, many of whom have chronic bilateral effusions with hearing loss and developmental comorbidities.
The impact of sampling on generalizability is particularly important when interpreting a diagnostic test. For instance, suppose an audiologist develops a new test for diagnosing middle ear effusion (MEE) . After testing 1000 children, she reports that 90% of children with a positive result did in fact have MEE (positive predictive value of 90%) . Yet when unselected kindergarten children were screened for MEE, the positive predictive value of the test is only 50%. Why does this occur? Because the baseline prevalence of MEE is lower in the kindergarten class (10% have MEE) than in the referral-based audiology population in which the test was developed (50% have MEE). Whereas the sensitivity and specificity of the test are unchanged in both situations, the predictive value is related to baseline prevalence (Bayes theorem); therefore, the ultimate utility of the test depends on the sample to which it will be applied.
No matter how elegant or seductive, a single study is rarely definitive. Science is a cumulative process that requires a large body of consistent and reproducible evidence before conclusions can be formed. When interpreting an exciting set of data, the cumulative basis of science is often overshadowed by the seemingly irrefutable evidence at hand—at least until a new study, by different investigators in a different environment, adds a new twist.
Habit 7 is the process of integration: reconciling findings with the existing corpus of known similar research. It is the natural consequence of habits 1 through 3 that deal with description and habits 4 through 6 that deal with analysis. Thus, data interpretation can be summarized in three words: describe, analyze, and integrate. This is a sequential process in which each step lays the foundation for subsequent ones, just as occurs for the six habits that underlie them.
Research integration begins by asking “Do the results make sense?” Statistically significant findings that are biologically implausible or that are inconsistent with other known studies can often be explained by hidden biases or design flaws that were initially unsuspected (habit 1). Improbable results can become statistically significant through biased data collection, natural history, placebo effects, unidentified confounding variables, or improper statistical analysis. A study with design flaws or improper statistical analysis is said to have low internal validity (see Table 2.12 ) and should be reanalyzed or discarded.
At the next level of integration, the study design that produced the current data is compared with the design of other published studies. The level of evidence for treatment benefits generally increases as we progress from uncontrolled observational studies (case reports, case series) to controlled observational studies (cross-sectional, retrospective, prospective) to controlled experiments (RCTs). Not all RCTs, however, are of high quality, and standards for analysis and reporting must be followed to ensure validity. Levels of research evidence are most often applied to studies of therapy or prevention ( Table 2.14 ), but they can also be defined for diagnosis and prognosis.
| Level a | Treatment Benefits | Prevalence or Incidence | Prognosis | Diagnostic Test Assessment |
|---|---|---|---|---|
| 1 | Systematic review of randomized trials or n -of-1 trials | Local and current random sample surveys (or census) | Systematic review of inception cohort studies b | Systematic review of cross-sectional studies with consistently applied reference standard and blinding |
| 2 | Randomized trial or observational study with dramatic effect | Systematic review of surveys that allows matching to local circumstances | Inception cohort studies b | Individual cross-sectional studies with consistently applied reference standard and blinding |
| 3 | Nonrandomized controlled cohort or follow-up study | Local nonrandom sample | Cohort study or control arm of randomized trial | Nonconsecutive studies or studies without consistently applied reference standards |
| 4 | Case series, case-control studies, or historically controlled studies | Case series | Case series or case-control studies or poor-quality prognostic study | Case-control studies, or studies with a poor or nonindependent reference standard |
| 5 | Expert opinion or mechanism-based reasoning from physiology, bench research, or first principles | Expert opinion or mechanism-based reasoning from physiology, bench research, or first principles | Expert opinion or mechanism-based reasoning from physiology, bench research, or first principles | Expert opinion or mechanism-based reasoning from physiology, bench research, or first principles |
a Level may be graded down based on study quality, imprecision, indirectness, inconsistency between studies, or because the absolute effect size is very small; level may be graded up if the effect size is large or very large.
b Inception cohort: group of individuals identified for subsequent study at an early, uniform point in the course of the specified health condition or before the condition develops.
Analysis of real world data (RWD) has become an increasingly important source of information that overcomes the limitations of RCTs regarding generalizability, implementability, and pragmatism in real-life clinical settings. RWD are data relating to patient health status, or the delivery of health care, that are routinely collected from electronic health records, administrative data (claims databases), population health surveys, or patient/disease registries. RWD are particularly useful for evaluating drug safety and effectiveness, but can also be used to create case-control studies that assess association.
A single study is rarely definitive; because science is cumulative, it mandates a large body of consistent and reproducible evidence before conclusions can be formed. For this reason, achieving the highest level of evidence (see Table 2.14 ) often requires a systematic review of available evidence, using explicit and reproducible criteria to locate, appraise, and synthesize articles with a minimum of bias. Meta-analysis is a form of systematic review that uses statistical techniques to derive quantitative estimates of the magnitude of treatment effects and their associated precision. Valid systematic reviews (and meta-analyses) address focused questions, assess the quality and combinability of articles, provide graphic and numeric summaries, and can be generalized to a meaningful target population. They also contain a flow diagram that shows the fate of articles as they pass through different phases of the review process, including identification, screening, eligibility, and inclusion. Graphic comparison of studies using forest and funnel plots helps assess publication trends, small-study bias, and overall combinability and consistency of included studies. Systematic reviews differ greatly from traditional “narrative” review articles ( Table 2.15 ) and are the preferred method for synthesizing research evidence.
| Characteristic | Narrative Review | Meta-Analysis |
|---|---|---|
| Research design | Free form | A priori protocol |
| Literature search | Convenience sample of articles deemed important by author | Systematic sample using explicit and reproducible article selection criteria |
| Data extraction | Selective data retrieval by one author | Systematic data retrieval by two or more authors to reduce error |
| Focus | Broad; summarizes a large body of information | Narrow; tests specific hypotheses and focused clinical questions |
| Emphasis | Narrative; qualitative summary | Numbers; quantitative summary |
| Validity | Variable; high potential for bias in article selection and interpretation | Good, provided articles are of adequate quality and combinability |
| Quality assessment | Usually not performed; all studies considered of equal quality | Assessed explicitly with criteria to measure risk of bias in study design, conduct, and reporting |
| Bottom line | Broad recommendations, often based on personal opinion; no discussion of heterogeneity | Estimates of effect size, based on statistical pooling of data; explicit assessment of heterogeneity among studies |
| Utility | Provides a quick overview of a subject area | Provides summary estimates for evidence-based medicine |
| Appeal to readers | Usually very high | Varies depending on focus |
Clinical practice guidelines are often the next step in evidence synthesis and may be defined as “statements that include recommendations intended to optimize patient care that are informed by a systematic review of evidence and an assessment of the benefits and harms of alternative care options.” Guidelines, therefore, build upon systematic reviews by incorporating values, preferences, and recommendation strengths, ideally based upon explicit and transparent processes that represent all stakeholders, including consumers. The best guidelines contain a limited number of actionable recommendations supported by distinct evidence profiles, and are accompanied by a plain language summary for patients and consumers.
Salient features of the most popular tests in otolaryngology journals are listed here. Note that each test is simply an alternative way to measure error (habit 4), not a self-contained method of data interpretation. Tests are chosen using the principles outlined in Tables 2.10 and 2.11 , then analyzed with readily available software, which can also help select the best test for a specific dataset. Explicit guidelines are available to help authors, editors, and reviewers identify the optimal format for reporting statistical results in medical publications.
The t test is a classic parametric test for comparing the means of two independent or matched (related) samples of numeric data; it is also called the Student t test.
A significant P value for independent samples implies a low probability that the mean values for the two groups are equal. When the samples are matched, a significant P value implies that the mean differences of the paired values are unlikely to be zero. Clinical importance is assessed by examining the magnitude of difference achieved and the associated 95% CI. Because valid results depend on relatively equal variances (the SD) within each group, a statistical test is required to verify this assumption (F test).
The t test produces an artificially low P value if the groups are small (fewer than 10 observations) or if they have an asymmetric distribution (one or more extreme outlying values); instead, a nonparametric test (Mann-Whitney U or Wilcoxon rank-sum test) should be used. If, however, each group contains more than 30 observations, the underlying distribution can deviate substantially from normality without invalidating the results. These t tests should never be used to compare more than two groups; for those, analysis of variance (ANOVA) is required. When the outcome of interest is time-to-event (e.g., cancer survival, duration of hospital stay, disease recurrence), survival analysis is more appropriate than a t test.
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here