Implant Attributes: Cantilever Beam Fixation

Cantilever

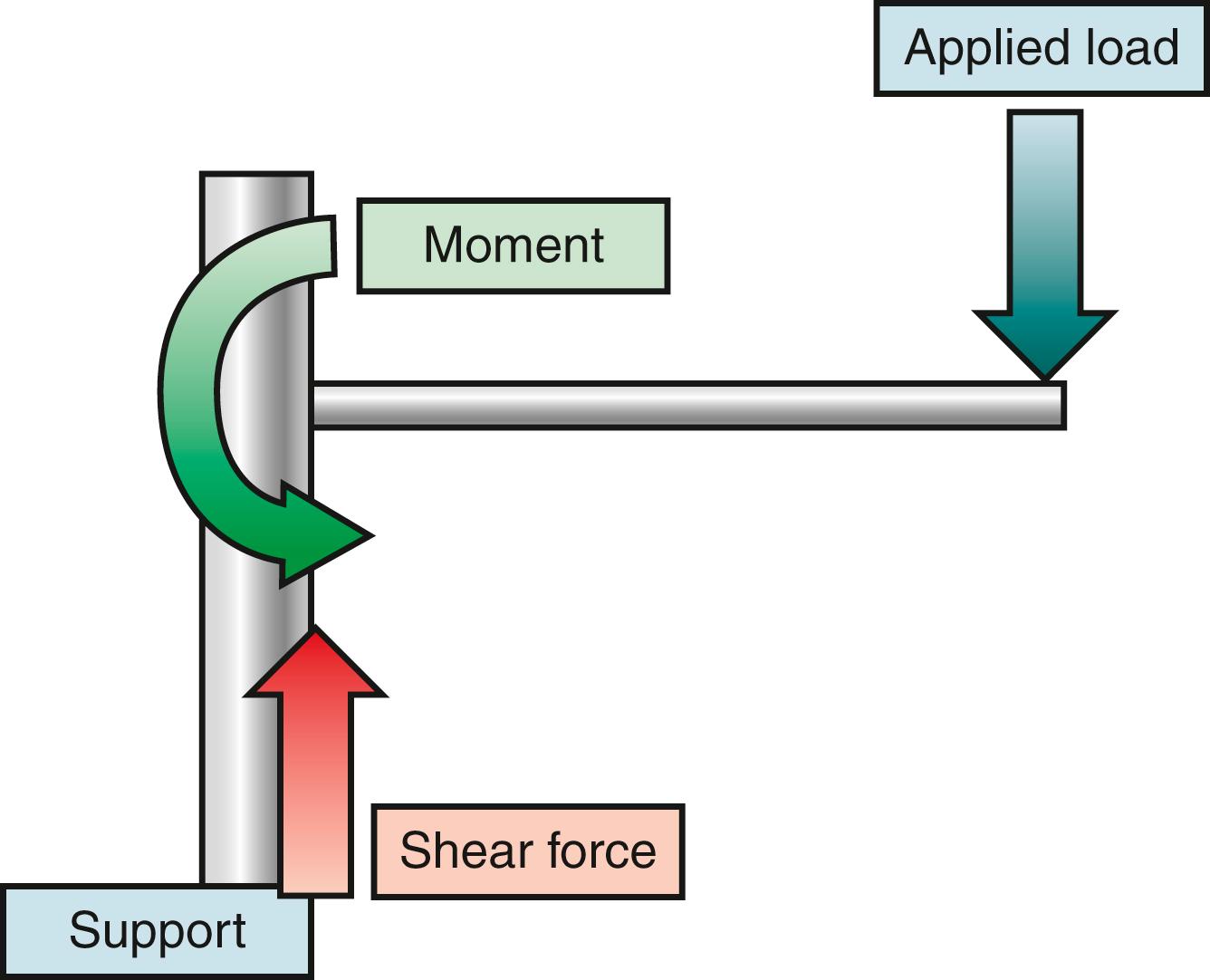
A cantilever beam is simply defined as a beam that is rigidly supported only at one end and carries a load. Examples of this commonly used engineering construct are numerous ( Fig. 14.1 ). Spinal instrumentation constructs using cantilever beams are also common. ^, It is important to recognize, however, that spinal instrumentation constructs are rarely composed of pure cantilever beams and may function otherwise in different clinical scenarios and when challenged with other stresses or moments.

An idealized cantilever beam is shown in Figure 14.2 . A load applied to the beam is resisted by shear force and a moment at the point of attachment to the support. In this idealized situation, with axial loading, the beam experiences a shear stress parallel to the vertical axis and a moment. This moment consists of a force and an instantaneous axis of rotation about which the force is applied.

Some important definitions that are frequently used throughout this chapter are listed here to facilitate better understanding of the biomechanical properties of the constructs depicted in this chapter and, more importantly, their clinical significance:

• 1.

  Shear/shearing stress. A stress that results from the shear of an elastic solid and is measured by the force per unit area exerted by adjacent mutually displaced layers upon each other in the plane common to both.

• 2.

  Moment. The product of a quantity (as a force) and the distance to a particular axis or point.

• 3.

  Yield strength. The stress at which a piece under strain is deformed some definite amount.

• 4.

  Moment of inertia of a mass. The ratio of the torque applied to a rigid body free to rotate about a given axis to the angular acceleration thus produced about that axis and equal to the sum of the products of each element of mass by the square of its distance from the given axis. Also known as rotational inertia.

Cantilevers in Spinal Instrumentation

Cantilevers are frequently used in modern constrained spinal instrumentation. Figure 14.3 depicts an idealized short-segment nonsegmental spinal instrumentation construct. Such a construct has been termed cantilever beam fixation. ^, Brief analysis reveals the presence of four potential cantilevers. Each screw is a cantilever beam supported by the vertebral body support. Each rod is a cantilever beam supported by a screw support. Analysis of such a complex system requires either significant simplification or separate analysis of each component before considering the properties of the entire system.

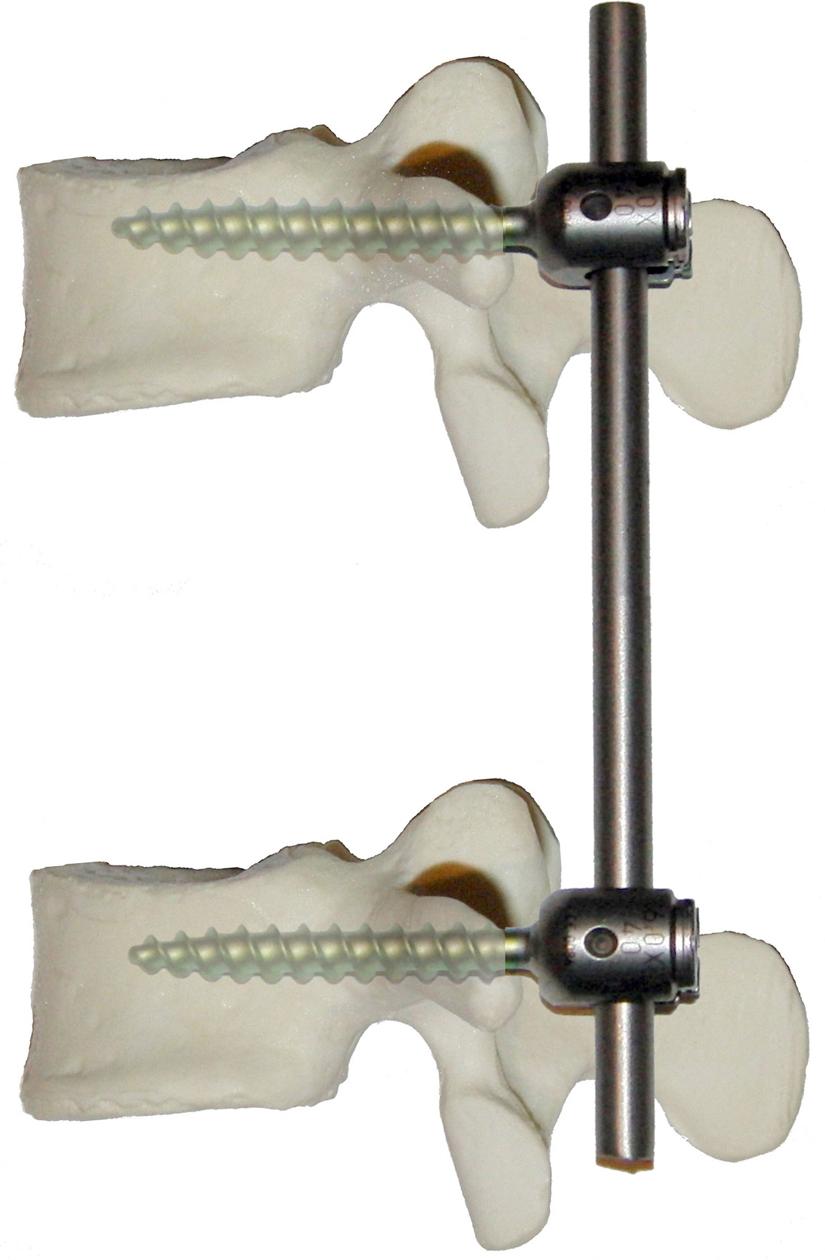
With regard to spinal fixation points, all screws function as cantilevers in response to vertical shear forces and sagittal moments. As will be discussed, screws may not function as cantilevers in response to other forces and moments. Hooks do not function as cantilevers. Although able to resist a shear force in certain circumstances, they in and of themselves are unable to resist a bending moment. Likewise, cables do not function as cantilevers because they function only when attached at both ends. When attached at only one end, cables resist neither shear force nor bending moments.

With regard to the longitudinal elements of spinal instrumentation constructs, a screw–rod interface functions as a cantilever only when the screw is rigidly attached to the longitudinal element. Nonconstrained plate and screw interfaces do not function as cantilevers because they are not rigidly attached to a support and are limited in their ability to resist an applied moment. Likewise, many “dynamic” stabilization systems incorporate a screw–rod interface that is very limited in its ability to resist a bending moment.

Bone–Screw Cantilever

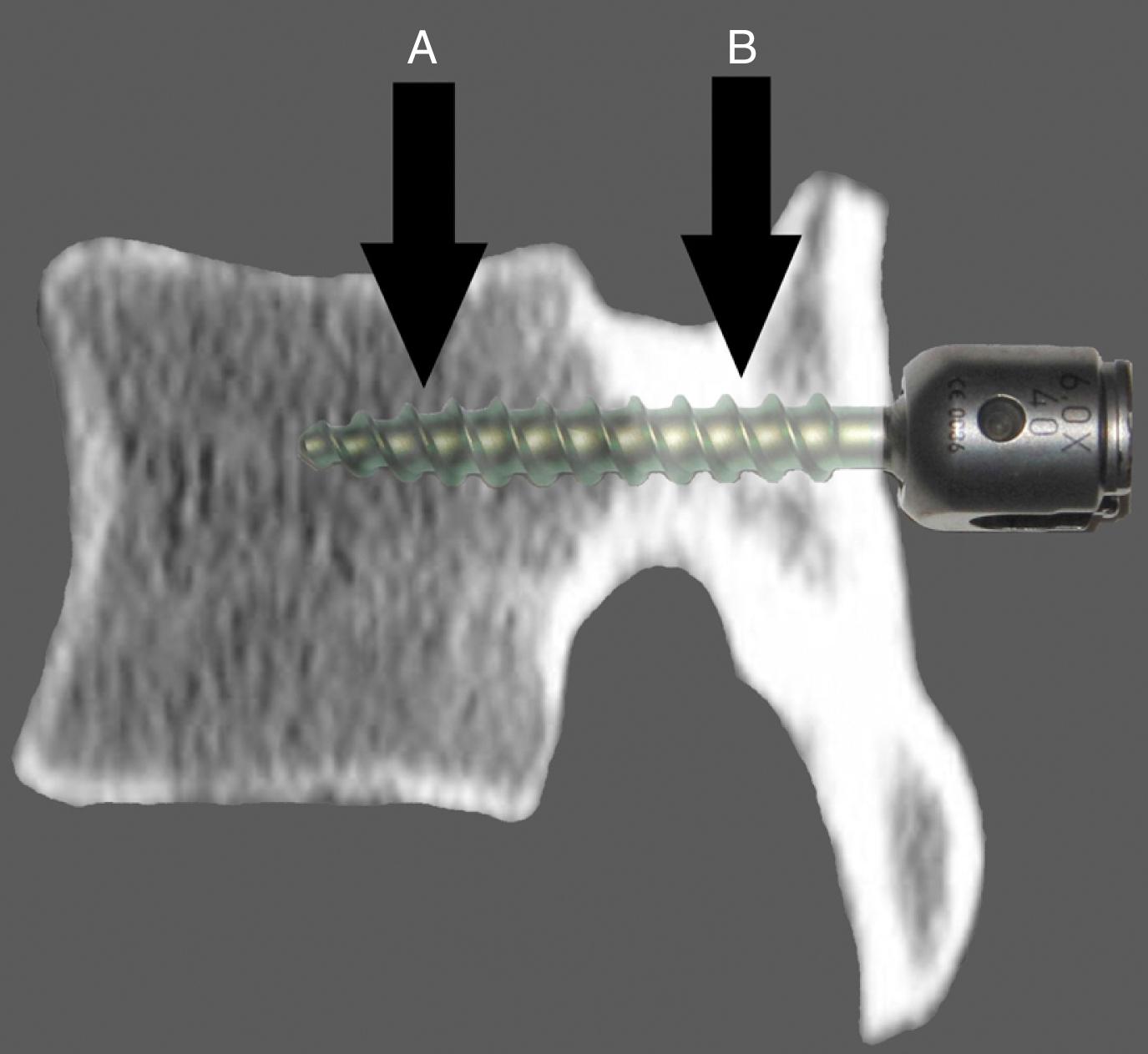
In the clinical situation, a transpedicular or vertebral body screw often functions as a cantilever. In this situation, the vertebral bone acts as the support. Both a shear stress and a rotational moment are resisted at the bone–screw interface.

Resistance to Shear Stress

The shear stress resistance of a typical screw is often much greater than the resistance of the bone in which is embedded. Resistance to shear stress at the bone–screw interface is primarily determined by the mechanical properties of the bone composing the vertebra. An idealized diagram of a vertebral body is shown in Figure 14.4 . The screw traverses a finite thickness of cortical bone, entering the cancellous bone of the central vertebral body. Shear stress resistance is a function of the relative contributions of the bone–screw interfaces in these locations. This contribution is related to the yield strength of the material, the stress at which a material begins to deform plastically, and the area of contact. Although the cancellous bone has significantly lower yield strength, the larger area of the bone–screw interface mitigates this property. The total shear stress resistance is the sum of the values for the engaged areas of cortical and cancellous bone.