General principles of pharmacokinetics and pharmacodynamics

Critically ill patients suffer from a variety of physiologic insults that result in a rapidly changing physiologic status, thus making appropriate drug dosing a challenging problem. Understanding how these changes affect pharmacokinetics and pharmacodynamics can result in improved dosing decisions. This chapter reviews the basic principles of pharmacokinetics and pharmacodynamics and how they may be affected by critical illness.

The terms pharmacokinetics and pharmacodynamics describe the amount of drug in the body at a given time and the pharmacologic effects caused by the drug. Pharmacokinetics describes the movement of a drug into, within, and out of the body over time, whereas pharmacodynamics explains the effects the drug has on the body. How a patient responds to therapy is a function of both the physiologic processes that dictate drug exposure (the changes in drug concentration over time) and the processes that govern how that exposure translates into pharmacodynamic effects. Understanding the pharmacokinetic parameters of clearance, volume of distribution, half-life, steady state, and absorption, along with pharmacodynamic principles such as receptor theory, potency, affinity, tolerance, and minimum effective concentration can enhance the treatment of critically ill patients.

General principles of pharmacokinetics

Clearance, volume of distribution, half-life, and bioavailability are four pharmacokinetic parameters that allow the clinician to better estimate dosing requirements. If the concentration of a drug in a sampled fluid (e.g., plasma, urine, saliva) correlates well with its pharmacologic response (therapeutic or toxic), then the application of pharmacokinetics is likely to be beneficial ( Fig. 139.1 ). This is especially true for drugs where lack of efficacy because of low exposure or toxicity because of high exposure pose significant risks to the patient.

Fig. 139.1, For concentration monitoring to be useful, there must be a strong relationship between concentration of the drug measured in an easily accessible fluid and concentration at the effect site.

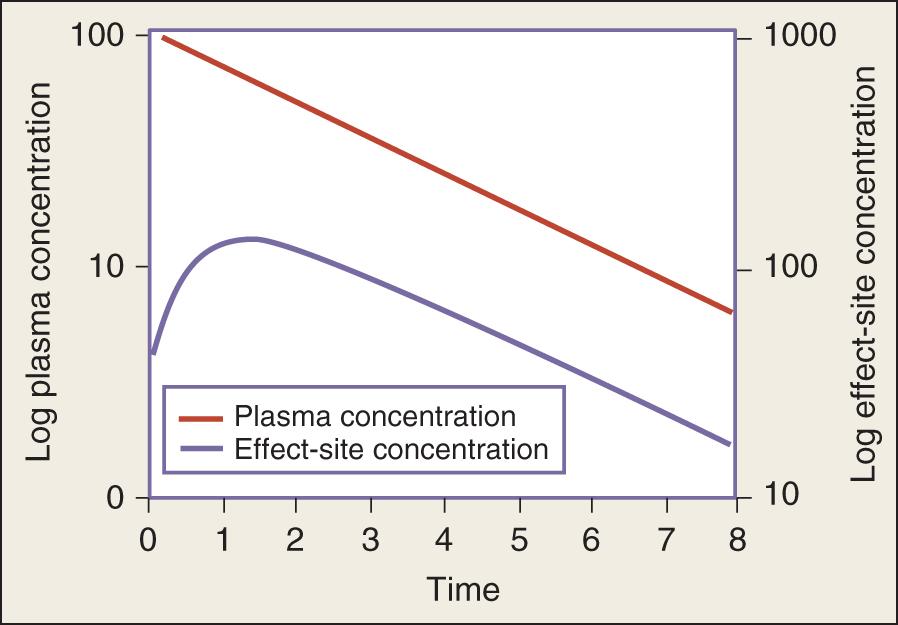
Measurement of the relationship between drug concentration and therapeutic or toxic response in a large number of patients enables the development of a therapeutic range or target concentration for that drug ( Fig. 139.2 ). ^, A multitude of host factors (e.g., hemodynamic status, decreased organ function, nutritional status, concurrent disease states) increase the likelihood that drug dosing based on individualized pharmacokinetic assessment will be beneficial. ^, Gender-related differences can occur in both pharmacokinetic and pharmacodynamic responses. Individual chapters in this text are devoted to many of these agents and their adjustments for dosage in patients with renal or hepatic failure.

Pharmacokinetic models

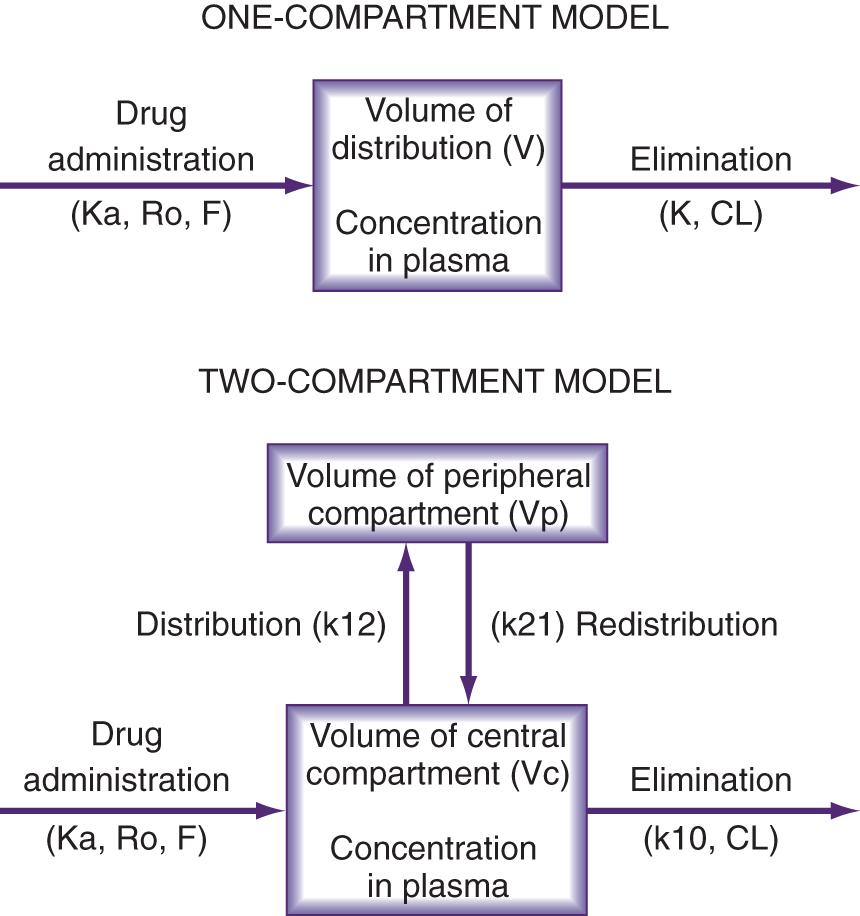
The pharmacokinetic concepts of clearance, volume of distribution, half-life, and bioavailability are based on enormously complex physiologic principles and use mathematical models that make many assumptions. Most clinically useful pharmacokinetic equations assume one- or two-compartment models (see Fig. 139.2 ).

When the drug enters the one-compartment model, it is assumed to be instantaneously and completely mixed in a given volume of distribution, resulting in a uniform concentration throughout the compartment. The rate constant K reflects the usual situation of elimination by a first-order, linear process. The drug is assumed to enter the compartment instantaneously in the case of an intravenous bolus dose. If the dosage is administered through oral or intramuscular routes, entry into the compartment is assumed to occur at a rate defined by a first-order absorption rate constant (Ka), whereas entry into the compartment is assumed to occur at a constant rate described by a zero-order rate constant (Ro) if the drug is administered by intravenous infusion. Bioavailability (F) is defined as the fraction of the administered dose that reaches the systemic circulation.

Clearance (CL) is a primary parameter that can be physiologically associated with a particular organ in the body such as the liver or kidney. Clearance is often expressed by the equation CL = K × V, leading to the impression that CL is a function of the parameters K and V. However, this arrangement of the equation is not correct from a physiologic point of view. CL and V are both primary parameters, and K is a secondary parameter. The first-order rate is determined by changes in either CL or V, and the equation is correctly written as K = CL/V.

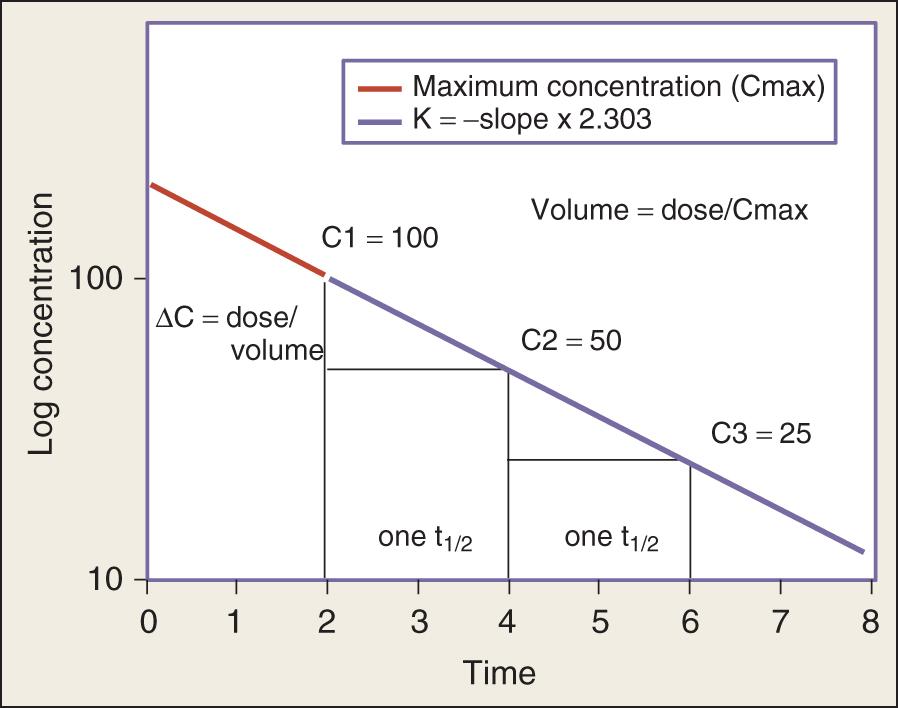
Half-life (t _1/2 ) is a useful measure of how quickly a drug is eliminated from the body and is related to the first-order elimination rate constant:

t_{1 / 2} = \frac{ln (2)}{K} = \frac{0.693}{K}

$t_{1 / 2} = \frac{ln (2)}{K} = \frac{0.693}{K}$

Specifically, t _1/2 defines the time taken for the drug concentration to decrease by one-half. In a linear pharmacokinetic system with first-order elimination, t _1/2 is constant, and it takes the same amount of time for the concentration to fall from 100 to 50 (arbitrary units) as it does to decline from 50 to 25 ( Fig. 139.3 ).

Fig. 139.3, Log concentration-time curve for a one-compartment model after intravenous administration, illustrating volume of distribution, elimination rate constant, and half-life.

The one-compartment model allows concentrations at any point in time to be calculated:

C 2 = C 1 × {exp}^{– K × Δt}

$C 2 = C 1 × {exp}^{– K × Δt}$

where Δt is the time between measurements C1 and C2. The monoexponentially decreasing concentration-time curve appears linear when plotted on semi-log coordinates.

Sometimes a drug does not instantly equilibrate with all tissues in the body. This can often be adequately described by a two-compartment model, which is characterized by a rapidly distributing central compartment and a more slowly equilibrating peripheral compartment ( Fig. 139.4 ). The equation describing the concentration-time profile for the two-compartment model is:

C = A × {exp}^{– α × t} + B × {exp}^{– β × t}

$C = A × {exp}^{– α × t} + B × {exp}^{– β × t}$

Fig. 139.4, Log concentration-time curve for a two-compartment model after intravenous administration, illustrating a distribution period (α) and postdistribution period (β). Concentrations C1 and C2 reflect both distribution and elimination processes, whereas concentrations C3 and C4 reflect postdistribution elimination processes.

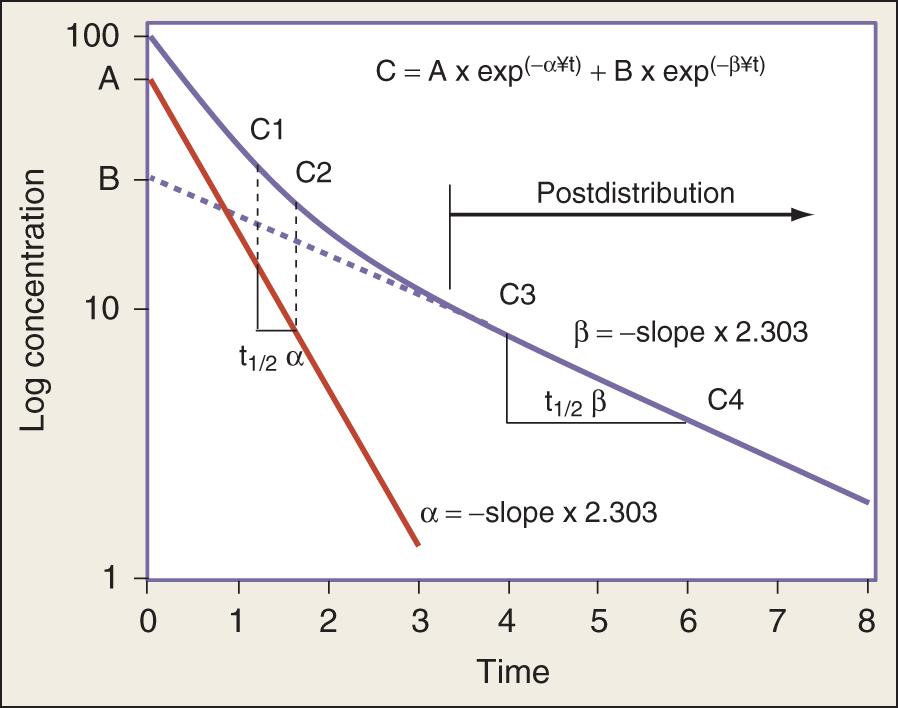
The distinguishing feature of this biexponential equation is that when plotted on semi-log coordinates, the concentrations are the sum of two distinct straight lines representing two half-lives. One is the terminal or β half-life, and the other is the rapid distribution or α half-life. As the rapid distribution exponential becomes negligible in the equation, the slower exponential term dominates, and the concentration-time profile resembles that of a single-compartment drug. Consequently, the equation:

C 2 = C 1 × {exp}^{– β × Δt}

$C 2 = C 1 × {exp}^{– β × Δt}$

in which β replaces K, can still be used to predict concentrations, as long as both C1 and C2 are in the postdistributive phase. This sum-of-exponentials approach can be extended to three-compartment or even more complex models, but it is difficult to obtain all the concentrations needed to characterize each exponent.

Clearance

CL is a primary pharmacokinetic parameter that measures the ability of the body to eliminate a drug. It is often stated that clearance is the volume of blood (plasma) that is completely cleared of drug per unit time. Although this is one way to define clearance, it does not capture the relationship between drug clearance (mL/min) and the rate of drug elimination (mg/hr). In pharmacokinetics, the general concept of clearance is also the rate of elimination relative to the concentration. In a first-order pharmacokinetic system, the rate of elimination is proportional to the drug concentration; clearance is this proportionality constant:

Rate of elimination = CL × concentration

$Rate of elimination = CL × concentration$

Clearance is clinically useful because it can be directly related to the organ of elimination. We can talk about renal clearance, hepatic clearance, or biliary clearance, and the sum of each of the individual clearances is the total body clearance. This allows us to adjust doses in response to changes in organ function. A patient with developing renal failure is likely to require a reduction of the dose of a drug that is eliminated by the kidney but not necessarily a dose reduction of a drug that is eliminated by the liver. For example, if the clearance of a drug is known to be 50% renal and 50% hepatic and renal function is decreased by 50%, it is necessary to reduce the dose by only 25% to maintain the same concentration.

The area under the curve (AUC) is a useful measure of drug exposure and results from dose and CL:

AUC = \frac{Dose}{CL}

$AUC = \frac{Dose}{CL}$

This concept is similar to a steady-state concentration (Css) being considered as the measure of drug exposure during a continuous intravenous infusion. The Css is solely a function of the infusion rate (Ro) and CL:

Css = \frac{Ro}{CL}

$Css = \frac{Ro}{CL}$

Notice that Css is not a function of the volume of distribution. Though counterintuitive, doubling the volume of distribution will not result in a halving of Css. The important point is that the equation is predicting the concentration at a steady state. During a constant infusion, rapidly doubling the volume of distribution will only transiently halve the concentration. If clearance remains unchanged, the concentration will return to the same Css.

With intermittent dosing, drug concentrations go up and come down during each dosing interval. The average Css (Css,avg) is a time-averaged concentration (i.e., the mean of all concentrations during the dosing interval); it is also a function of clearance and the dosing rate. In the case of oral administration, the dosing rate is a function of the dose administered (D), dosing interval (τ), and F:

Css, avg = \frac{F × D / τ}{CL}

$Css, avg = \frac{F × D / τ}{CL}$

As before, the overall drug exposure is not influenced by the volume of distribution, but it does change in proportion to changes in clearance or the dosing rate through changes in F, D, or τ.

Volume of distribution

The volume of distribution (V) is another primary pharmacokinetic parameter and is useful for determining the change in drug concentration for a given dose. After an intravenous bolus dose in a one-compartment pharmacokinetic model, the change in concentration (ΔC) between the maximum concentration (Cmax) and the concentration immediately before the dose is administered is a function of the dose (D) and the V:

ΔC = \frac{D}{V}

$ΔC = \frac{D}{V}$

This equation is useful for predicting both the concentration after a first bolus dose and the increase in concentration at any point in time after a bolus dose. If a concentration before a bolus dose is known, the equation can be used to predict the increase in concentration after the dose is administered (see Fig. 139.3 ). This equation is also useful for estimating the dose needed to reach a given concentration. If it is known that the volume of distribution is 0.45 L/kg and a Cmax of 10 mg/L is desired after the loading dose, the dose is estimated to be 10 mg/L × 0.45 L/kg = 4.5 mg/kg. This equation only predicts loading doses and not maintenance doses. A steady-state condition is not necessary, which is common in critical care.

The value for the volume of distribution does not necessarily coincide with any particular physiologic space. The veracity of this statement becomes readily apparent when one considers a drug such as digoxin, which has a volume of distribution of approximately 440 L. Clearly, a volume of distribution of that magnitude cannot have a relationship to any physiologic space in an average-sized human. Therefore the term apparent volume of distribution is often used.

The concept of the volume of distribution gets more complex when more than one compartment is needed to describe the pharmacokinetics of a drug. Mathematically, the volume of distribution is a hypothetical volume that is needed to relate the amount of drug in the body to a measured concentration in a fluid (plasma). Unlike the one-compartment model, wherein the entire drug in the body is regarded as being in a single compartment until it is eliminated, drug also circulates through additional compartments in a multicompartment model. In this situation, the volume of distribution must increase as drug distributes to other compartments until distribution equilibrium among all compartments is reached. Technically, an infinite number of volumes of distribution are observed as this equilibration process occurs, but only three are commonly defined. The volume of distribution of the central compartment (Vc) is the volume of the usual sampling compartment; it is always the smallest volume term. Immediately after the administration of an intravenous bolus, all added drug is in the central compartment, and Vc can be used to calculate a change in concentration.

The volume of distribution increases over time until a distribution equilibrium is reached among all compartments. This is the largest value for the volume of distribution. The fact that the distribution equilibrium has occurred can be discerned from a log concentration versus time plot (see Fig. 139.4 ). The curve becomes log linear when the rate of drug entry into each peripheral compartment equals the rate of return from each compartment. Because it is often calculated using the clearance and β or terminal elimination half-life, this volume is often called V _β :

V_{β} = \frac{CL}{β}

$V_{β} = \frac{CL}{β}$

The steady-state volume of distribution (Vss) is the sum of the volumes of all the compartments in the model. If a drug were infused to steady state, Vss would be the proportionality constant relating Css to the total amount of drug in the body.

You're Reading a Preview

Become a Clinical Tree membership for Full access and enjoy Unlimited articles

Become membership

If you are a member. Log in here