Computational Approaches for Accurate Rotor Localization in the Atria

Introduction

Experimental and clinical data from a number of laboratories support the hypothesis that both acute and persistent atrial fibrillation (AF) in some animal models and groups of human patients is not random. Studies analyzing the spatiotemporal organization of waves and dominant frequency (DF) in the isolated sheep heart demonstrate that AF maintenance depends on reentrant, or so-called “rotor,” sources localized mainly in the left atrium (LA) and generating fibrillatory conduction in their periphery. Subsequent translational studies analyzing the organization of DFs in human AF have suggested that, in paroxysmal AF, reentrant AF sources were localized primarily on the LA posterior wall near the pulmonary veins (PVs) but elsewhere in persistent AF. More direct evidence for the presence and role of rotors in driving human AF has since been provided in numerous invasive and noninvasive ^, mapping studies. Several such studies showed that AF could be eliminated by directly ablating AF-driving sources that exhibit high-frequency periodic activity, based on either electrogram analysis, DF analysis, or panoramic endocardial mapping. ^, ^, The results demonstrated that AF ablation based on a target-specific strategy aimed at eliminating localized sources, whether identified as reentries, rotors, focal discharges, or high-frequency sites, is at least as efficacious and potentially safer than empirically isolating all the PVs.

Nevertheless, controversies persist regarding the particular role of rotors as a mechanism underlying AF maintenance, ^, which likely are the result of different mapping and processing methods being used in different laboratories. The focus of this chapter is to present and discuss recent computational methods to better understand the localization of rotors with optical and electrical methods. The chapter begins with a brief mechanistic description of the rotor followed by an outline of the phase and frequency domain approaches used to enhance the accuracy in the understanding of rotor dynamics in AF. The chapter then illustrates and discusses the application of the phase and frequency approaches for identifying reentries or rotors in optical mapping, computer simulation, and intracardiac and noninvasive multielectrode electrical mapping studies. Ultimately, having a better understanding and localization of rotors responsible for AF maintenance may help in the design of the most suitable ablation strategy for each individual AF patient.

Action Potential Rotor

Cardiac muscle belongs to a class of systems called excitable media because each of its component cells can switch between bistable states designated as resting or excited (action potential [AP]) electrical potential states. When cells are coupled to form a two-dimensional (2D) or three-dimensional (3D) syncytium, the governing electrical, diffusion, and biochemical principles of such a system render it capable of generating AP waves that may self-organize and swirl continuously, forming vortices, which are termed rotors . Fig. 35.1 reproduces one of the first ever visualized rotors in cardiac tissue. Part A, taken from an optical mapping experiment, shows selected snapshots of AP depolarizations (in white ) forming a periodic wave with a full-cycle spectrum of action phases (rest, depolarization, plateau, and repolarization) and pivoting around a phase singularity point (SP) in space that is otherwise an ordinary point like any other point in the medium. In part B, a time-space plot along a line crossing the center of the rotation in part A ( red line ), together with superimposed traces at various times, illustrates the fact that the area around the SP is characterized as having a low-amplitude activity ( red arrow ), which remains unexcited even though it is highly excitable. Such an area is known generally as the core of the rotor as illustrated in the diagram of part C, which represents a counterclockwise spinning rotor with a characteristic isopotential activation front whose velocity decreases as the wave front curvature increases with decreased distance from the core. At the point of critical curvature, the propagation of the AP is blocked and only electrotonically mediated depolarizing currents invade the core region. In return, the unexcited core exerts an electrotonic repolarizing influence on the excited regions within its immediate surroundings, acting to reduce their action potential amplitude and duration. The closer such regions are to the center, the briefer the depolarization phase duration will be. In fact, at the area near the critical curvature, the AP duration (APD) shortening effect is such that the front and tail of a wave meet so their isopotential curves become a single continuous curve. Thus a unique feature of rotors, one that distinguishes them from so-called “anatomic reentry” (i.e., reentry around an unexcitable center), is the joining of the wave front with its repolarizing tail. The joined front tail and the SP are the basis for the identification and localization of rotors in the heart.

Fig. 35.1, Rotor in Optical Mapping (the Gold Standard) and Low Amplitude at the Core Region.

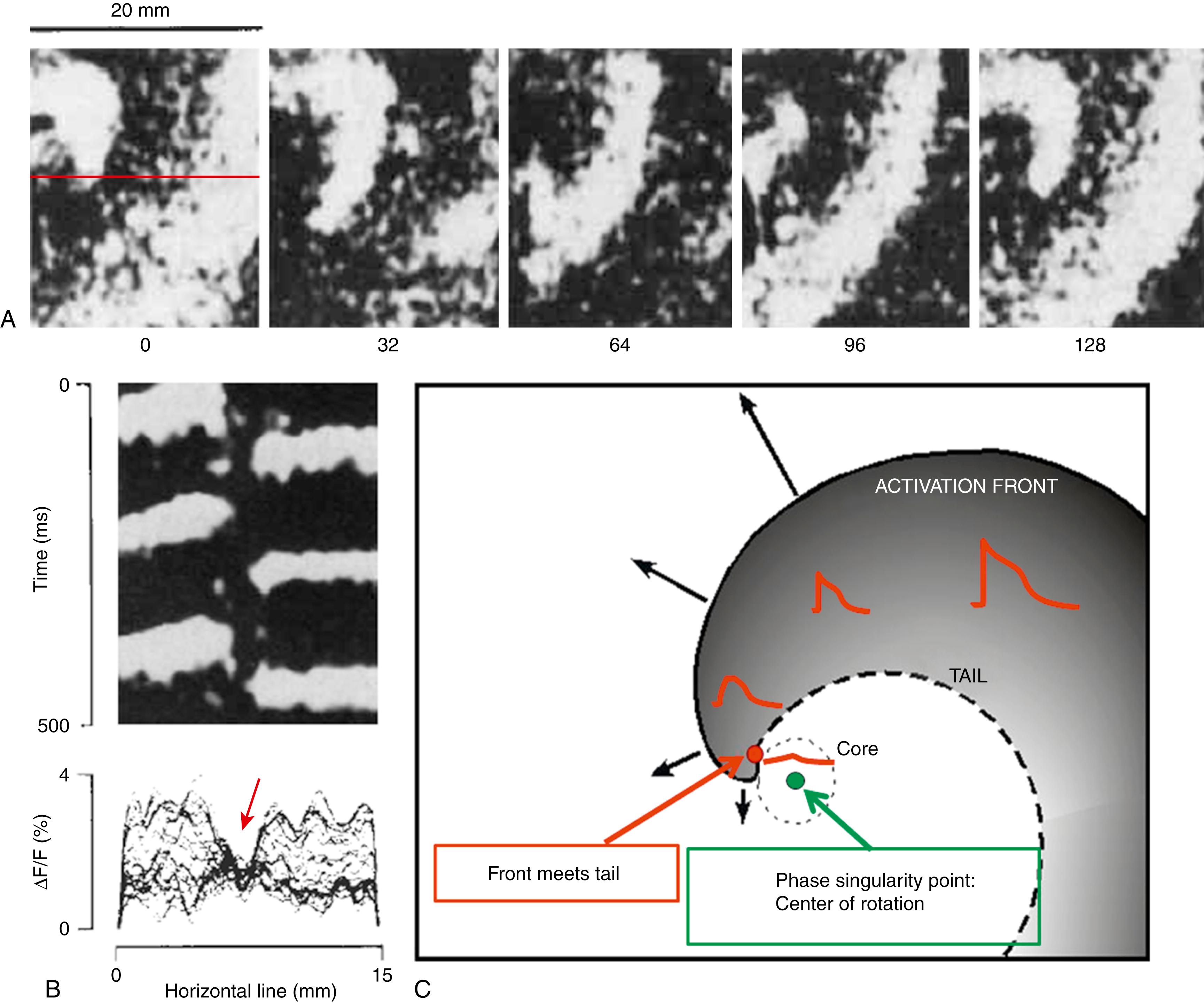
In practice, rotor localization is difficult. As illustrated in Fig. 35.1 , the voltage near the rotor SP can be very small in comparison with the AP amplitude, and the center of rotation may also meander and drift. Therefore marking the activations for rotor localization might be inaccurate. Spatiotemporal characterization and localization of rotors can, however, be markedly enhanced by separately analyzing the instantaneous and stationary properties that are derived, respectively, from analyses in the phase and the frequency domains, as discussed in the following sections.

Phase Representation Of The Action Potential Time Course

In 1998 Gray et al. introduced a unique phase mapping algorithm that markedly enhanced the characterization of complex spatiotemporal patterns of cardiac fibrillation. A transmembrane signal derived from the fluorescence of a potentiometric dye that recorded with a high-resolution video camera each pixel location of the ventricular epicardium exhibited repetitive APs, each of which was transformed into a quasiclosed trajectory in 2D phase space that could be represented by its phase. Accordingly, because the AP recorded by a single pixel during fibrillation is a function of time, the fluorescence of each pixel at time t, F(t), was plotted against the fluorescence of the same pixel offset by a time interval τ, F(t−τ). A cyclic return map of F(t) versus F(t−τ) was constructed, which allowed for the phase of the AP’s sequence, θ(t), to be defined as the angle of the coordinate x = F(t) and y = F(t−τ) in a 2D fluorescence space around the mean fluorescence for that given pixel, with repeating values between 0 and 2π (or between 0 and 360 degrees), represented as a continuous color scheme. The value of the time lag τ is chosen such that the phase can be uniquely specified during the course of a wave rotation. In nonlinear dynamics, an optimal choice of τ for such a task is one that minimizes the mutual dependence of the two variables. Thus the value of τ can be chosen so that it is the lowest lag that significantly minimizes the correlation between F(t) and F(t−τ). The aforementioned criterion, however, is difficult to implement because it needs to be evaluated separately for each pixel. The simple possibility for minimizing the correlation by selecting the lagging time τ to be a quarter of the average interbeat interval is also hampered because of the variability in the frequency content of the signals during fibrillation. Fortunately, the Hilbert transform automatically provides an optimal F(t−τ) counterpart for F(t), enabling the most reliable possible phase calculation of the AP sequences, regardless of their varying frequency content.

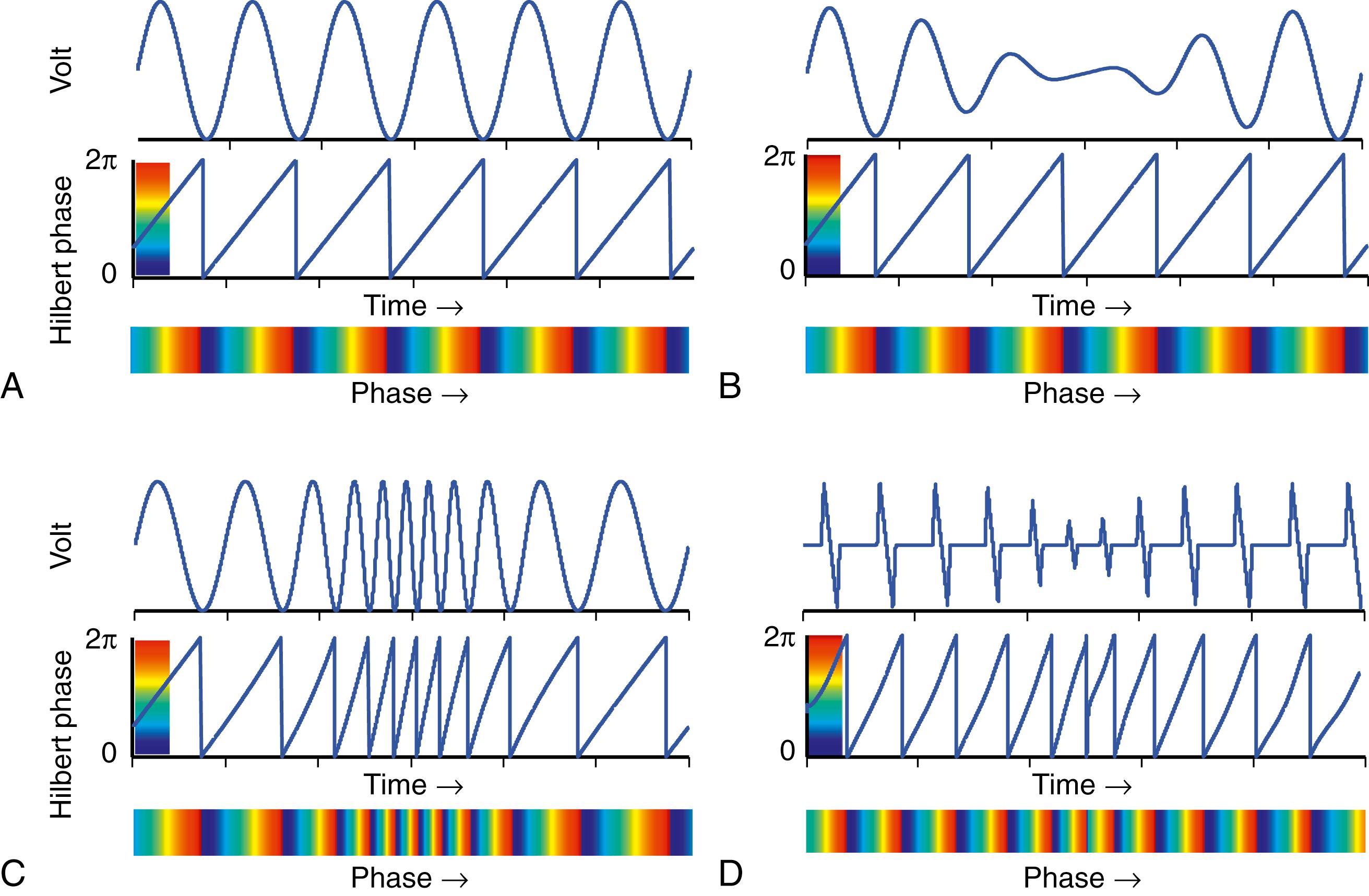
Fig. 35.2 presents a few examples demonstrating the performance and robustness of the Hilbert transform approach to resolve the time course phase of quasiperiodic signals. In part A, a simulated harmonic wave with a constant frequency and amplitude, shown in the upper trace, is subject to Hilbert transform and phase calculation, as shown in the lower trace. The time course of the phase is seen to repeat its linear increase between 0 and 2π radians (or between 0 and 360 degrees), which can be color coded between blue and red and displayed as a color bar time series (bottom). Part B reproduces a similar processing on a wave simulated to have a constant frequency, but with a transient modulation of amplitude reduction, such as expected near the pivoting point of a rotor, as shown in Fig. 35.1 . As can be appreciated by the phase trace and color-coded time series at the bottom, the phase calculation based on the Hilbert transform is not affected by the transient amplitude reduction and displays the correct phase time course, as in part A. Part C demonstrates that the Hilbert transform correctly calculates the instantaneous phase, even when the frequency is not constant. In part D, the Hilbert-based phase of a preprocessed signal simulated is calculated to have not only transient alterations in amplitude and frequency but also a nonharmonic morphology that is more comparable to unipolar electrical recordings. Even in this case, the calculated phase time course accurately follows the simulated cycles, showing the robustness of the Hilbert method for capturing instantaneous amplitude and frequency modulations. It should be noted, however, that the interpretation of the phase as the stage of the AP cycle in experimental and clinical cases is not always straightforward. Interpretation may benefit from additional processing and filtering justified on physiologic grounds, as demonstrated in the following section.

Fig. 35.2, Phase Representation of the Action Potential Using the Hilbert Transform.

You're Reading a Preview

Become a Clinical Tree membership for Full access and enjoy Unlimited articles

Become membership

If you are a member. Log in here