Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Electrical potentials exist across the membranes of virtually all cells of the body. Some cells, such as nerve and muscle cells, generate rapidly changing electrochemical impulses at their membranes, and these impulses are used to transmit signals along the nerve or muscle membranes. In other types of cells, such as glandular cells, macrophages, and ciliated cells, local changes in membrane potentials also activate many of the cell’s functions. This chapter reviews the basic mechanisms whereby membrane potentials are generated at rest and during action by nerve and muscle cells. See .
In Figure 5-1 A , the potassium concentration is great inside a nerve fiber membrane but very low outside the membrane. Let us assume that the membrane in this case is permeable to the potassium ions but not to any other ions. Because of the large potassium concentration gradient from the inside toward the outside, there is a strong tendency for potassium ions to diffuse outward through the membrane. As they do so, they carry positive electrical charges to the outside, thus creating electropositivity outside the membrane and electronegativity inside the membrane because of negative anions that remain behind and do not diffuse outward with the potassium. Within about 1 millisecond, the potential difference between the inside and outside, called the diffusion potential, becomes great enough to block further net potassium diffusion to the exterior, despite the high potassium ion concentration gradient. In the normal mammalian nerve fiber, the potential difference is about 94 millivolts, with negativity inside the fiber membrane.
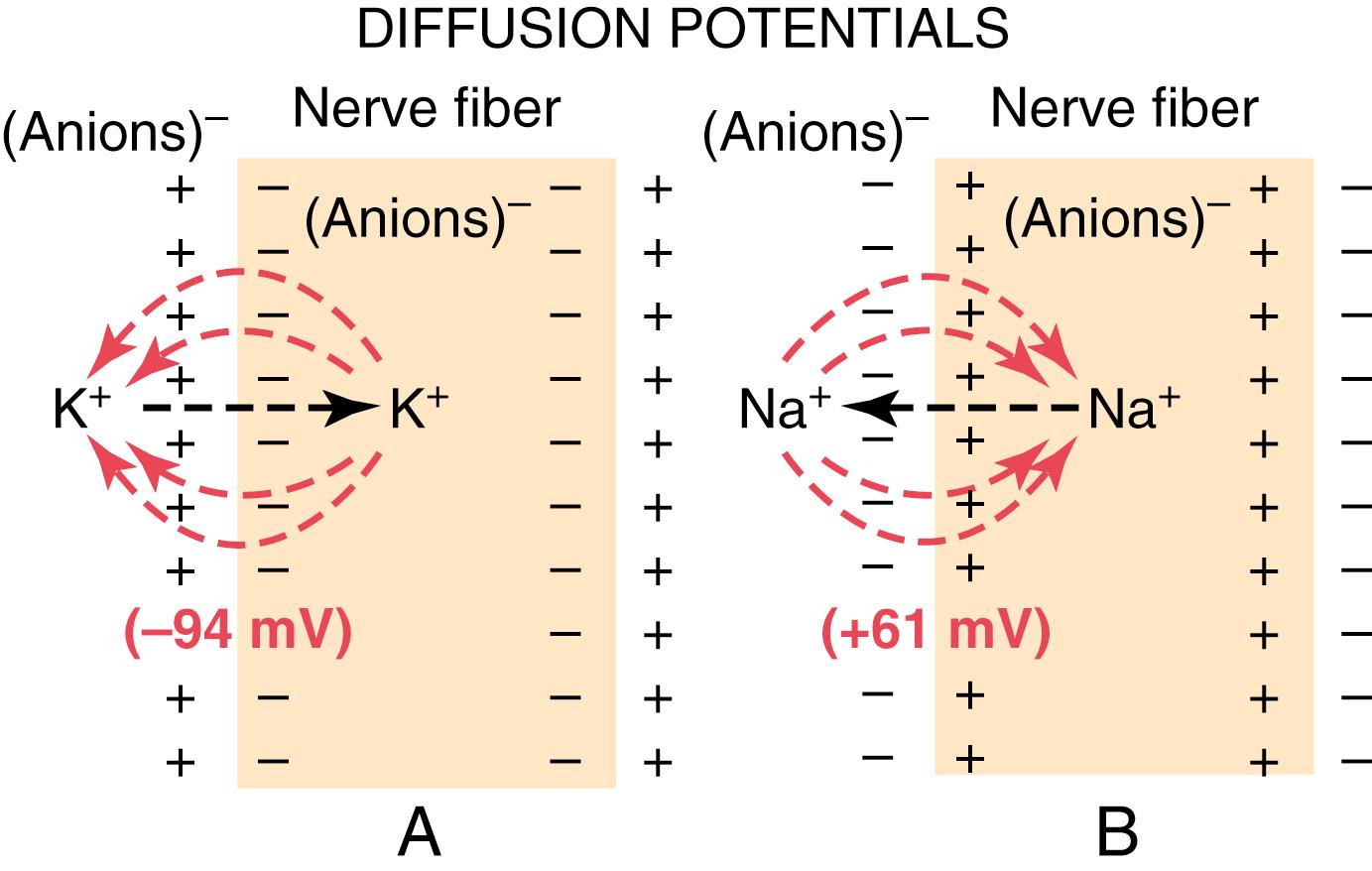
Figure 5-1 B shows the same phenomenon as in Figure 5-1A , but this time with a high concentration of sodium ions outside the membrane and a low concentration of sodium ions inside . These ions are also positively charged. This time, the membrane is highly permeable to the sodium ions but is impermeable to all other ions. Diffusion of the positively charged sodium ions to the inside creates a membrane potential of opposite polarity to that in Figure 5-1 A , with negativity outside and positivity inside. Again, the membrane potential rises high enough within milliseconds to block further net diffusion of sodium ions to the inside; however, this time, in the mammalian nerve fiber, the potential is about 61 millivolts positive inside the fiber.
Thus, in both parts of Figure 5-1 , we see that a concentration difference of ions across a selectively permeable membrane can, under appropriate conditions, create a membrane potential. Later in this chapter, we show that many of the rapid changes in membrane potentials observed during nerve and muscle impulse transmission result from such rapidly changing diffusion potentials.
The diffusion potential across a membrane that exactly opposes the net diffusion of a particular ion through the membrane is called the Nernst potential for that ion, a term that was introduced in Chapter 4 . The magnitude of the Nernst potential is determined by the ratio of the concentrations of that specific ion on the two sides of the membrane. The greater this ratio, the greater the tendency for the ion to diffuse in one direction and therefore the greater the Nernst potential required to prevent additional net diffusion. The following equation, called the Nernst equation, can be used to calculate the Nernst potential for any univalent ion at the normal body temperature of 98.6°F (37°C):

where EMF is the electromotive force and z is the electrical charge of the ion (e.g., +1 for K + ).
When using this formula, it is usually assumed that the potential in the extracellular fluid outside the membrane remains at zero potential, and the Nernst potential is the potential inside the membrane. Also, the sign of the potential is positive (+) if the ion diffusing from inside to outside is a negative ion, and it is negative (−) if the ion is positive. Thus, when the concentration of positive potassium ions on the inside is 10 times that on the outside, the log of 10 is 1, so the Nernst potential calculates to be −61 millivolts inside the membrane.
When a membrane is permeable to several different ions, the diffusion potential that develops depends on three factors: (1) the polarity of the electrical charge of each ion; (2) the permeability of the membrane (P) to each ion; and (3) the concentration (C) of the respective ions on the inside (i) and outside (o) of the membrane. Thus, the following formula, called the Goldman equation or the Goldman-Hodgkin-Katz equation, gives the calculated membrane potential on the inside of the membrane when two univalent positive ions, sodium (Na + ) and potassium (K + ), and one univalent negative ion, chloride (Cl − ), are involved:
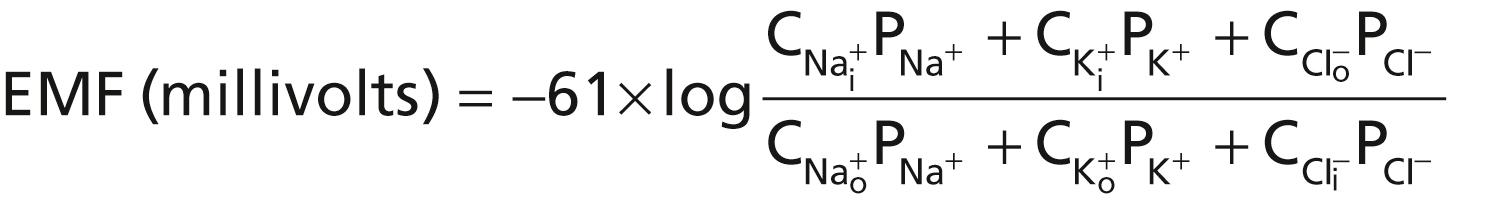
Several key points become evident from the Goldman equation. First, sodium, potassium, and chloride ions are the most important ions involved in the development of membrane potentials in nerve and muscle fibers, as well as in the neuronal cells. The concentration gradient of each of these ions across the membrane helps determine the voltage of the membrane potential.
Second, the quantitative importance of each of the ions in determining the voltage is proportional to the membrane permeability for that particular ion. If the membrane has zero permeability to sodium and chloride ions, the membrane potential becomes entirely dominated by the concentration gradient of potassium ions alone, and the resulting potential will be equal to the Nernst potential for potassium. The same holds true for each of the other two ions if the membrane should become selectively permeable for either one of them alone.
Third, a positive ion concentration gradient from inside the membrane to the outside causes electronegativity inside the membrane. The reason for this phenomenon is that excess positive ions diffuse to the outside when their concentration is higher inside than outside the membrane. This diffusion carries positive charges to the outside but leaves the nondiffusible negative anions on the inside, thus creating electronegativity on the inside. The opposite effect occurs when there is a gradient for a negative ion. That is, a chloride ion gradient from the outside to the inside causes negativity inside the cell because excess negatively charged chloride ions diffuse to the inside while leaving the nondiffusible positive ions on the outside.
Fourth, as explained later, the permeability of the sodium and potassium channels undergoes rapid changes during transmission of a nerve impulse, whereas the permeability of the chloride channels does not change greatly during this process. Therefore, rapid changes in sodium and potassium permeability are primarily responsible for signal transmission in neurons, which is the subject of most of the remainder of this chapter.
In some cells, such as the cardiac pacemaker cells discussed in Chapter 10 , the membrane potential is continuously changing, and the cells are never “resting”. In many other cells, even excitable cells, there is a quiescent period in which a resting membrane potential can be measured. Table 5-1 shows the approximate resting membrane potentials of some different types of cells. The membrane potential is obviously very dynamic in excitable cells such as neurons, in which action potentials occur. However, even in nonexcitable cells, the membrane potential (voltage) also changes in response to various stimuli, which alter activities for the various ion transporters, ion channels, and membrane permeability for sodium, potassium, calcium, and chloride ions. The resting membrane potential is, therefore, only a brief transient state for many cells.
| Cell Type | Resting Potential (mV) |
|---|---|
| Neurons | −60 to −70 |
| Skeletal muscle | −85 to −95 |
| Smooth muscle | −50 to −60 |
| Cardiac muscle | −80 to −90 |
| Hair (cochlea) | −15 to −40 |
| Astrocyte | −80 to −90 |
| Erythrocyte | −8 to −12 |
| Photoreceptor | −40 (dark) to −70 (light) |
When multiple ions contribute to the membrane potential, the equilibrium potential for any of the contributing ions will differ from the membrane potential, and there will be an electrochemical driving force (V df ) for each ion that tends to cause net movement of the ion across the membrane. This driving force is equal to the difference between the membrane potential (V m ) and the equilibrium potential of the ion (V eq ) Thus, V df = V m – V eq .
The arithmetic sign of V df (positive or negative) and the valence of the ion (cation or anion) can be used to predict the direction of ion flow across the membrane, into or out of the cell. For cations such as Na + and K + , a positive V df predicts ion movement out of the cell down its electrochemical gradient, and a negative V df predicts ion movement into the cell. For anions, such as Cl − , a positive V df predicts ion movement into the cell, and a negative V df predicts ion movement out of the cell. When V m = V eq , there is no net movement of the ion into or out of the cell. Also, the direction of ion flux through the membrane reverses as V m becomes greater than or less than V eq ; hence, the equilibrium potential (V eq ) is also called the reversal potential .
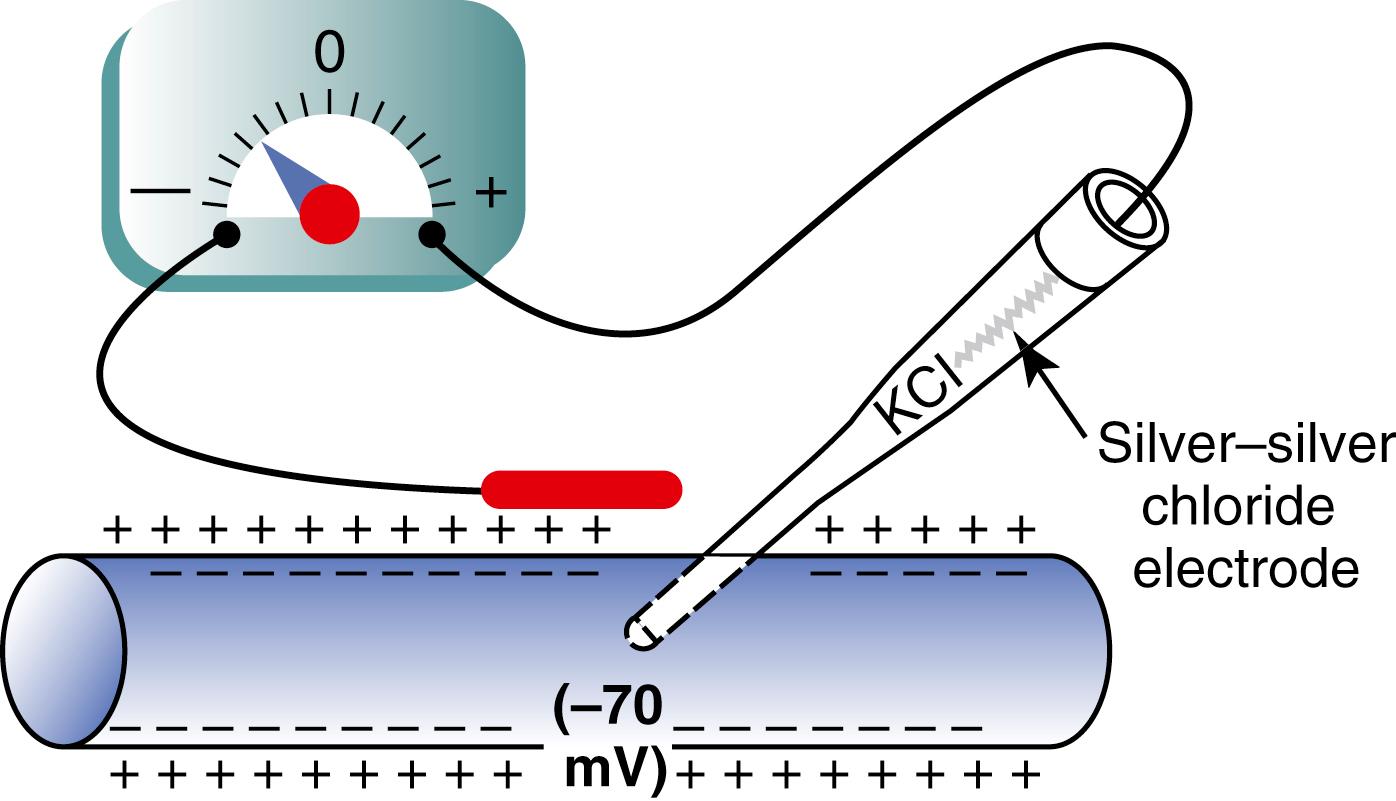
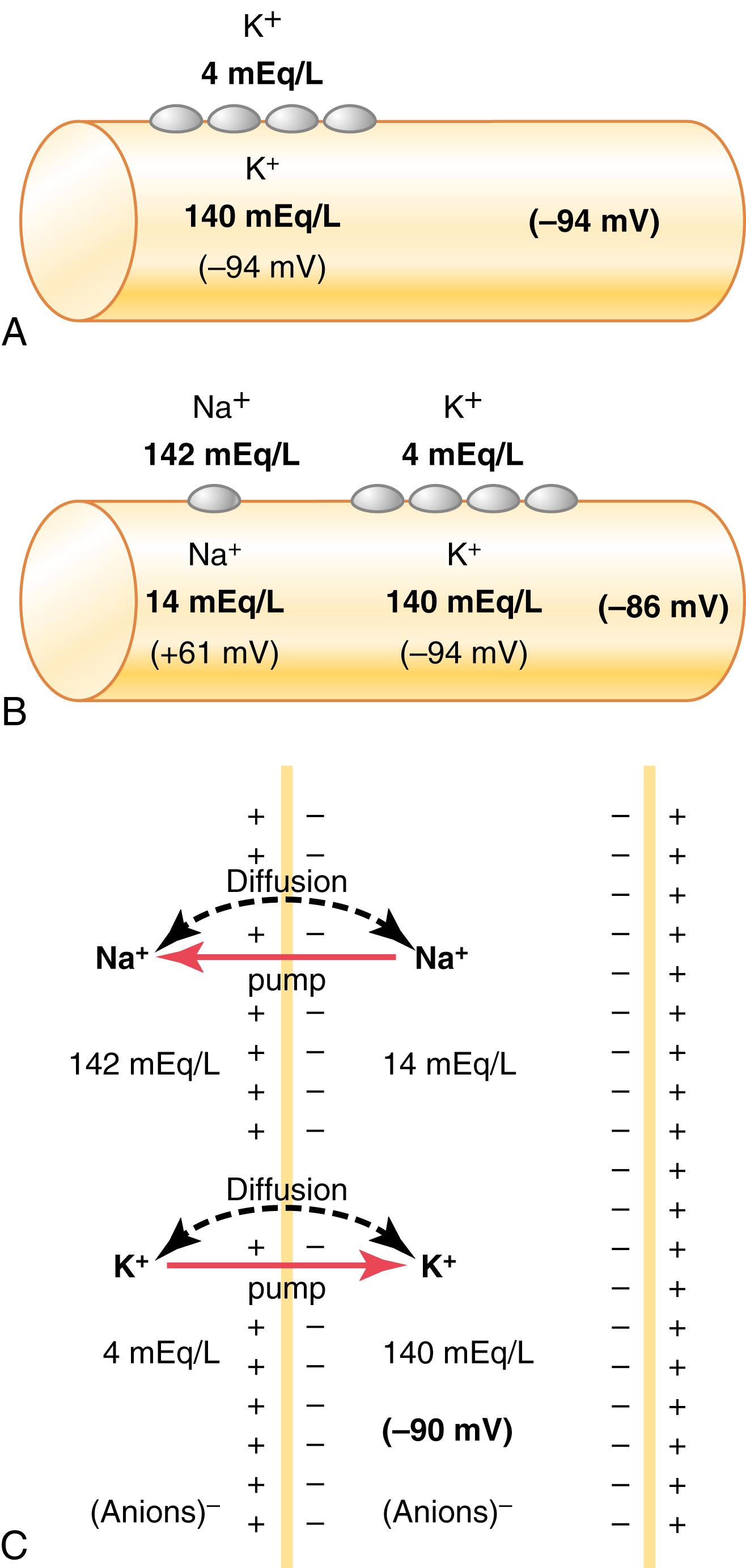
The method for measuring the membrane potential is simple in theory but often difficult in practice because of the small size of most of the cells and fibers. Figure 5-2 shows a small micropipette filled with an electrolyte solution. The micropipette is impaled through the cell membrane to the interior of the fiber. Another electrode, called the indifferent electrode, is then placed in the extracellular fluid, and the potential difference between the inside and outside of the fiber is measured using an appropriate voltmeter. This voltmeter is a highly sophisticated electronic apparatus that is capable of measuring small voltages despite extremely high resistance to electrical flow through the tip of the micropipette, which has a lumen diameter usually less than 1 micrometer and a resistance of more than 1 million ohms. For recording rapid changes in the membrane potential during transmission of nerve impulses, the microelectrode is connected to an oscilloscope, as explained later in the chapter.
The lower part of Figure 5-3 shows the electrical potential that is measured at each point in or near the nerve fiber membrane, beginning at the left side of the figure and passing to the right. As long as the electrode is outside the neuronal membrane, the recorded potential is zero, which is the potential of the extracellular fluid. Then, as the recording electrode passes through the voltage change area at the cell membrane (called the electrical dipole layer ), the potential decreases abruptly to −70 millivolts. Moving across the center of the fiber, the potential remains at a steady −70-millivolt level but reverses back to zero the instant it passes through the membrane on the opposite side of the fiber.
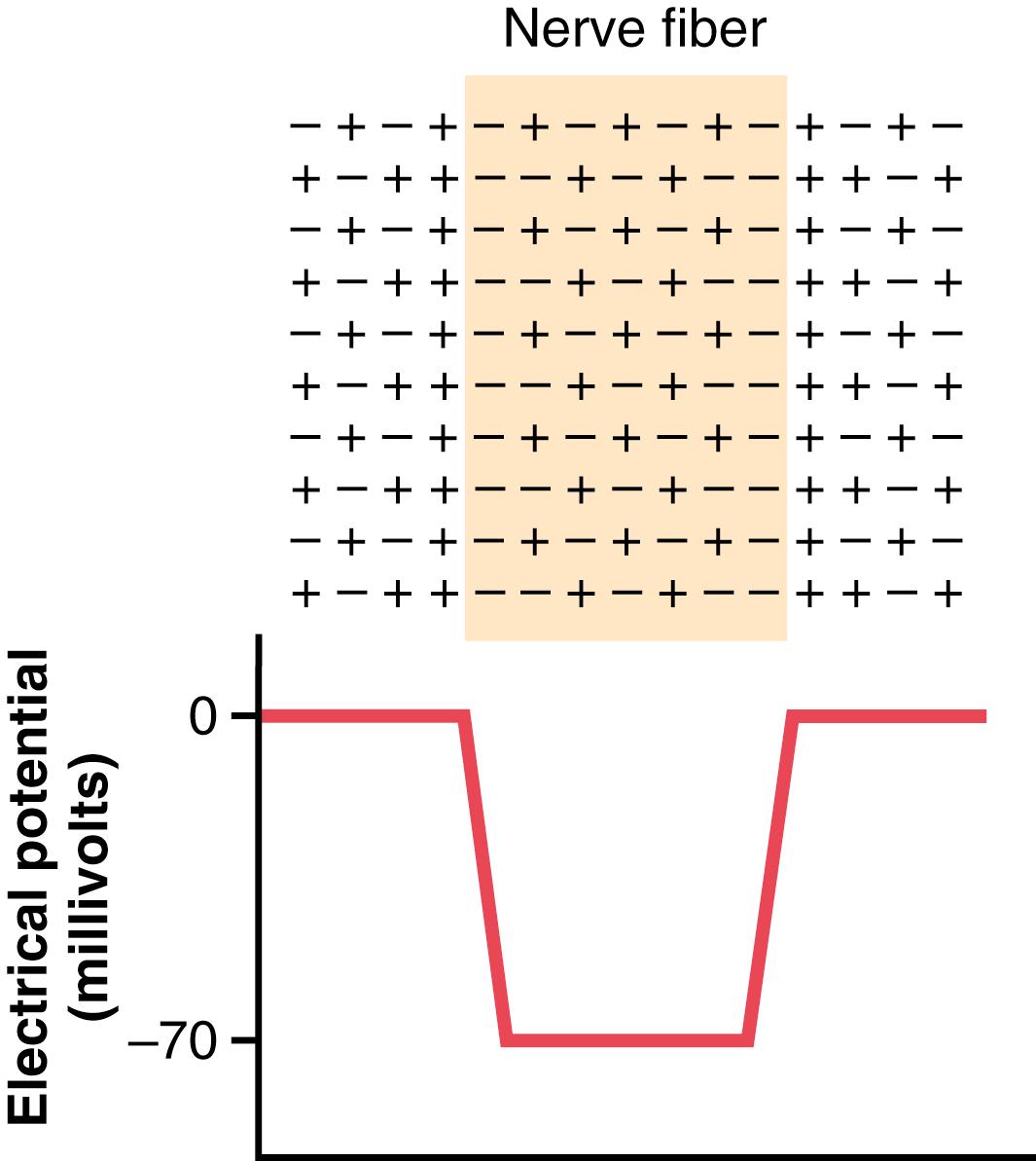
To create a negative potential inside the membrane, only enough positive ions to develop the electrical dipole layer at the membrane itself must be transported outward. The remaining ions inside the nerve fiber can be both positive and negative, as shown in the upper panel of Figure 5-3 . Therefore, transfer of an incredibly small number of ions through the membrane can establish the normal resting potential of −70 millivolts inside the nerve fiber, which means that only about 1/3,000,000 to 1/100,000,000 of the total positive charges inside the fiber must be transferred. Also, an equally small number of positive ions moving from outside to inside the fiber can reverse the potential from −70 millivolts to as much as +35 millivolts within as little as 1/10,000 of a second. Rapid shifting of ions in this manner causes the nerve signals discussed in subsequent sections of this chapter.
The resting membrane potential of large nerve fibers when they are not transmitting nerve signals is about −70 millivolts. That is, the potential inside the fiber is 70 millivolts more negative than the potential in the extracellular fluid on the outside of the fiber. In the next few paragraphs, the transport properties of the resting nerve membrane for sodium and potassium and the factors that determine the level of this resting potential are explained.
Recall from Chapter 4 that all cell membranes of the body have a powerful Na + -K + pump that continually transports sodium ions to the outside of the cell and potassium ions to the inside, as illustrated on the left side in Figure 5-4 . Note that this is an electrogenic pump because three Na + ions are pumped to the outside for each two K + ions to the inside, leaving a net deficit of positive ions on the inside and causing a negative potential inside the cell membrane.
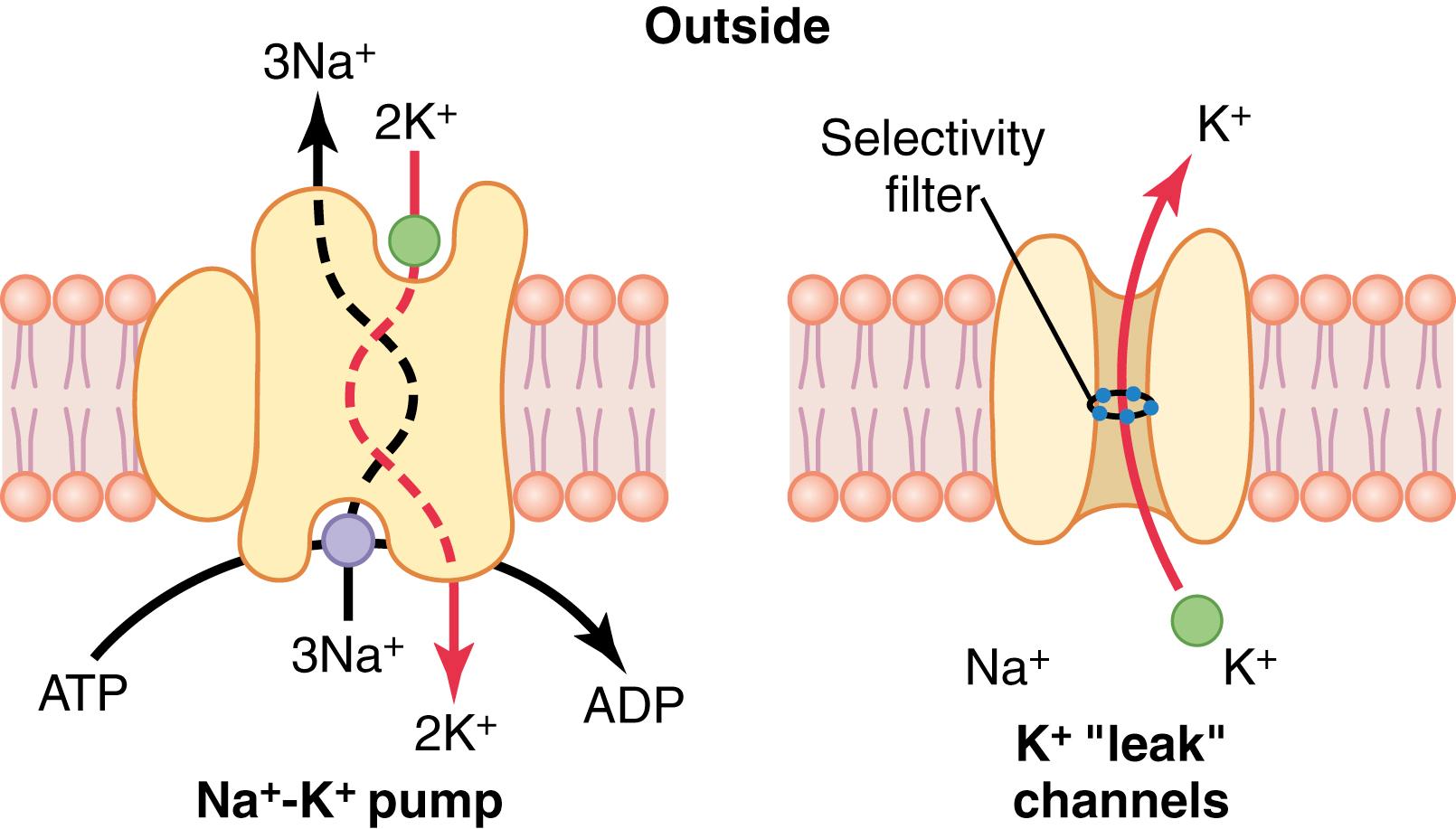
The Na + -K + pump also causes large concentration gradients for sodium and potassium across the resting nerve membrane. These gradients are as follows:
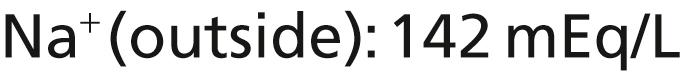
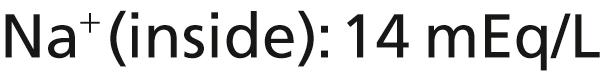
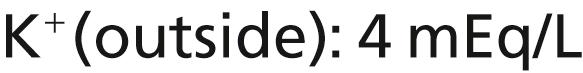

The ratios of these two respective ions from the inside to the outside are as follows:
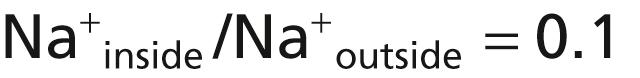

The right side of Figure 5-4 shows a channel protein (sometimes called a tandem pore domain, potassium channel , or potassium [K + ] “leak” channel ) in the nerve membrane through which potassium ions can leak, even in a resting cell. The basic structure of potassium channels was described in Chapter 4 ( Figure 4-4 ). These K + leak channels may also leak sodium ions slightly but are far more permeable to potassium than to sodium, normally about 100 times as permeable. As discussed later, this differential in permeability is a key factor in determining the level of the normal resting membrane potential.
Figure 5-5 shows the important factors in the establishment of the normal resting membrane potential. They are as follows.
In Figure 5-5A , we assume that the only movement of ions through the membrane is diffusion of potassium ions, as demonstrated by the open channels between the potassium symbol (K + ) inside and outside the mem brane. Because of the high ratio of potassium ions inside to outside, 35:1, the Nernst potential corresponding to this ratio is −94 millivolts because the logarithm of 35 is 1.54, and this, multiplied by −61 millivolts, is −94 millivolts. Therefore, if potassium ions were the only factor causing the resting potential, the resting potential inside the fiber would be equal to −94 millivolts, as shown in the figure.
Figure 5-5B shows the addition of slight permeability of the nerve membrane to sodium ions, caused by the minute diffusion of sodium ions through the K + -Na + leak channels. The ratio of sodium ions from inside to outside the membrane is 0.1, which gives a calculated Nernst potential for the inside of the membrane of +61 millivolts. Also shown in Figure 5-5B is the Nernst potential for potassium diffusion of −94 millivolts. How do these interact with each other, and what will be the summated potential? This question can be answered by using the Goldman equation described previously. Intuitively, one can see that if the membrane is highly permeable to potassium but only slightly permeable to sodium, the diffusion of potassium contributes far more to the membrane potential than the diffusion of sodium. In the normal nerve fiber, the permeability of the membrane to potassium is about 100 times as great as its permeability to sodium. Using this value in the Goldman equation, and considering only sodium and potassium, gives a potential inside the membrane of −86 millivolts, which is near the potassium potential shown in the figure.
In Figure 5-5C , the Na + -K + pump is shown to provide an additional contribution to the resting potential. This figure shows that continuous pumping of three sodium ions to the outside occurs for each two potassium ions pumped to the inside of the membrane. The pumping of more sodium ions to the outside than the potassium ions being pumped to the inside causes a continual loss of positive charges from inside the membrane, creating an additional degree of negativity (about −4 millivolts additional) on the inside, beyond that which can be accounted for by diffusion alone.
Therefore, as shown in Figure 5-5C , the net membrane potential when all these factors are operative at the same time is about −90 millivolts. However, additional ions, such as chloride, must also be considered in calculating the membrane potential.
In summary, the diffusion potentials alone caused by potassium and sodium diffusion would give a membrane potential of about −86 millivolts, with almost all of this being determined by potassium diffusion. An additional −4 millivolts is then contributed to the membrane potential by the continuously acting electrogenic Na + -K + pump, and there is a contribution of chloride ions. As mentioned previously, the resting membrane potential varies in different cells from as low as around −10 millivolts in erythrocytes to as high as −90 millivolts in skeletal muscle cells.
Nerve signals are transmitted by action potentials, which are rapid changes in the membrane potential that spread rapidly along the nerve fiber membrane. Each action potential begins with a sudden change from the normal resting negative membrane potential to a positive potential and ends with an almost equally rapid change back to the negative potential. To conduct a nerve signal, the action potential moves along the nerve fiber until it comes to the fiber’s end.
The upper panel of Figure 5-6 shows the changes that occur at the membrane during the action potential, with the transfer of positive charges to the interior of the fiber at its onset and the return of positive charges to the exterior at its end. The lower panel shows graphically the successive changes in membrane potential over a few 10,000ths of a second, illustrating the explosive onset of the action potential and the almost equally rapid recovery.
The successive stages of the action potential are as follows.
The resting stage is the resting membrane potential before the action potential begins. The membrane is said to be “polarized” during this stage because of the −70 millivolts negative membrane potential that is present.
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here