Waveforms and mechanisms in neuromodulation

Waveform shapes

Much like analyzing how we have come to describe music, we can break down waveforms into a few very fundamental aspects. An electrical field-creating source transfers the field to the tissue via a metallic electrode contact, or more than one and is either “on” or “off.” A note in music either occurs or it does not occur in time. By this binary reality, the device either is creating an electric field of some sort or is not, at any given moment. If it had been “on” and is now “off,” there may also be lingering effects from it having been “on” that are still operative on the tissue. Conversely, if the tissues had been affected in the past by a stimulus, they are unlikely to be in exactly the same state when the stimulus is again “on” that they were in at previous times. So many variables, each with their own time constants, are brought into the mix of any type of stimulus on tissue that when one contemplates how any of the effects can be predicted the problem quickly can seem to be overwhelming. Cell membranes, secondary messengers, a variety of transmitters and receptors, all with their own time constants, longer term changes in receptor up- and downregulation, and other proteomic and genomic changes dynamically altered over multiple time scales all make the problem staggering. Moreover, many of these variables remain unknown in their values before, during, and after our attempts are made to analyze the process. As such, we are often left with only the behavioral level to measure, not by choice, but by necessity.

But as in music, notes are there for a time, or not. They linger in the vibrations of air for a time—variable times. They have different frequencies, are held on for varying amounts of time, and are strung together in time using a variety of cadences, rigidly rhythmic or less so. And a note can have a variety of characteristics like attack shape which alter our perception of it. That is pretty much everything needed to describe music in any composition, and likewise the nature of the waveform used in any neuromodulation device.

Currently, neuromodulation devices use, for the most part, square waves that are delivered in a static frequency with a static pulsewidth either continuously without pause, or in packets as so-called “bursts”. Amplitudes are adjusted in programming sessions using feedback from patients most of the time or based on prior anecdotal information regarding what amplitudes seemed to have been beneficial ( Fig. 6.1 ).

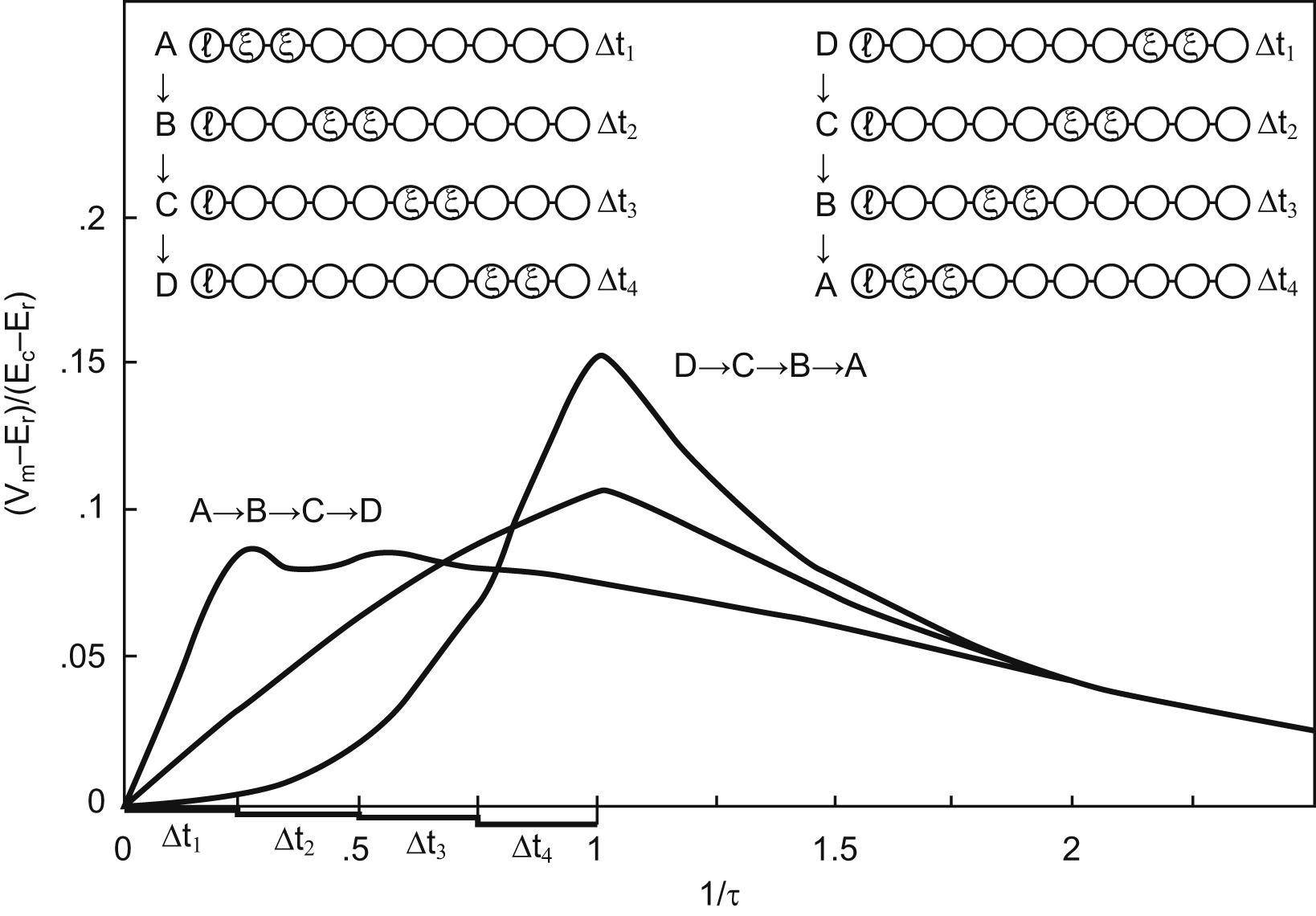
The amount of energy delivered to the tissues can be determined as a multiplication of frequency × pulsewidth × amplitude, for a given impedance, per second. This value in and of itself, however, neglects several aspects of how neural tissues respond to various waveforms with their own nonlinear dynamics to the timing and other features of the energy delivery. A simple illustration of this can be shown in work from Rall [ ] ( Fig. 6.2 here), studying dendritic processing in a passive cable model of dendrites and current injection at several locations along the dendrite from distal to the axon hillock and cell body in general and closer to it. If one uses the same total energy in each case, but in the first instance, injects a pulse of current from distal moving closer to the cell body in order, or in the second instance starting with the first pulse at the cell body and then moving distally, it becomes obvious that what the axon hillock “sees” over time, and which is the determinant largely of whether the neuron will fire an AP itself or not, is a completely different rise and fall of current in both cases, though their total energy delivered was the same. Extrapolating to this discussion, it is therefore not a foregone conclusion that 100 Hz, delivered with a 50 us pulsewidth at 2 mA is going to do the same thing as 50 Hz delivered with a 200 uS pulsewidth at 1 mA, or to a 5 kHz stimulus at 10 uS pulsewidth delivered at 0.2 mA for that matter. All of these waveforms, albeit all using steadily produced square waves without pauses between the anode and cathode phases, will likely have grossly different effects on an axon, though they use the same total energy delivery. Additionally, not all axons are the same, some are myelinated, some not, some large in diameter others smaller, and almost certainly they will each have slightly or radically different membrane parameters.

Most spinal cord stimulation has, until very recently, used lower frequency (<200 Hz) charge-balanced square waves, with pulsewidths in the range of 50–300 uS, and amplitudes typically within the range of 1–5 mA. Most systems now deliver “constant-current” stimulation, based on the intercontact impedances (which doesn't necessarily give any accurate information on what actually reaches the spinal cord), and don't make instantaneous adjustments to account for movement of the spinal cord itself, which is known to be occurring every few milliseconds with breathing, heartbeat, and physical movement and posture. This factor will be discussed further below.

It is also important to understand the efficiency for nerve fiber activation using various waveform “shapes.” This has been studied in detail (see Refs. [ , ]). The long-standing hypothesis that a rising exponential waveform shape was most energy efficient was refuted and, given the variations in cell dynamics, pulsewidth, and waveform shape, no shape was found to be simultaneously energy, charge, and power-optimal. The main factor in refuting this hypothesis turned out to be that prior work had analyzed linear membrane models for charge integration. Nonlinear models which took into account that the threshold rises with stimulation (accommodation) gave a more realistic and sophisticated view of how neurons actually respond. Not all neurons integrate current with the same set of membrane parameters or have the same degree of threshold accommodation. Moreover, spatial aspects of fiber location relative to the current source contribute to waveform shape efficiency as well, such that axon orientation, intervening tissue characteristics, and distance all can alter what shape may be most efficient for a particular circumstance. More detailed analysis of waveform shape and efficiency under various conditions and using different techniques has been performed and is further reviewed concisely in Ref. [ ].