Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Biomechanics is an interdisciplinary field that uses the principles of mechanics to improve the human body through design, development, and analysis of equipment, systems, and therapies. This biomechanical knowledge can help in understanding the loading of the musculoskeletal system and its mechanical responses, which can be used to determine normal function, predict changes, and propose interventions. More specifically, basic biomechanics explores forces and moments required for movement and balance of the human body by muscle recruitment and the consequence of internal forces on loading of soft tissues. This chapter explores biomechanics in terms of four topics: statics, dynamics, mechanics of materials, and applications. Additionally, examples of these concepts are provided throughout the chapter to illustrate how they can be directly applied to sports medicine.
Understanding the basic units of measure for biomechanics is important in describing the dimensional or spatial analyses. There are three primary dimensions—length, time, and mass—from which secondary dimensions are subsequently derived ( Table 2.1 ). Metric unit measurements are commonly used in the field of biomechanics to describe such dimensions and are also used in this chapter. One measurement not described in Table 2.1 is that used for angular descriptions. The unit for angles is typically defined in terms of radians or degrees.
| Dimensions | SI Unit |
|---|---|
| Primary | |
| Length | Meter (m) |
| Time | Second (s) |
| Mass | Kilogram (kg) |
| Secondary | |
| Area | m 2 |
| Volume | m 3 |
| Velocity | m/s |
| Acceleration | m/s 2 |
| Force | Newton (N) = kg • m/s 2 |
| Pressure/stress | Pascal (Pa) = N/m 2 |
| Moment/torque | N • m |
| Work/energy | Joule (J) = N • m |
| Power | J/s |
Most of the physical quantities encountered in mechanics are either scalars or vectors. Scalar quantities describe only the magnitude of an element and are used for concepts such as time, length, speed, mass, temperature, volume, work, power, and energy. In contrast, both a magnitude and a direction are associated with vector quantities. Examples of vector quantities are displacement, force, moment, velocity, and acceleration. The magnitude of an object's velocity is identical to its speed, but the velocity vector also contains information about the direction of motion. Graphically, a vector is represented as an arrow, with the orientation of the arrow indicating its line of action or direction. For example, the force of gravity is a vector quantity that can be represented by a downward arrow at an object's center of mass. Typically vectors are represented in a Cartesian coordinate system.
A coordinate system is a frame of reference for a structure or system. Coordinate systems are spatial tools that are useful in describing body position and orientation and the directionality of all vector quantities. To apply mechanical principles to a system, all vector quantities must be expressed with respect to the same coordinate system. Several types of coordinate systems are available, but the most commonly used in sports medicine research is the Cartesian coordinate system. This system can be either two- or three-dimensional. All axes are perpendicular to one another (a condition known as orthogonality) and have both positive and negative components. A vector quantity contains a component in each dimension corresponding to the magnitude associated with each axis. In a two-dimensional system, the horizontal and vertical axes are typically labeled “x” and “y,” respectively. In a three-dimensional system, the “z”-axis is added. This axis lies perpendicular to both the x- and y-axes, with its positive side determined by the right-hand rule. This rule states that if you align the index finger of your right hand with the positive x-axis and the middle finger with the positive y-axis, your thumb will be pointing in the positive direction of the z-axis. Similarly, the right-hand rule can be used to determine the positive and negative directions of angles and moments about a specified axis. While the thumb of your right hand is aligned with the rotational axis, your fingers will curl in the positive direction of rotation. These rules are very important in establishing the correct spatial quantities within a designated coordinate system.
An anatomic coordinate system is a Cartesian coordinate system with each axis representing anatomic directions such as superior-inferior, medial-lateral, and anterior-posterior. The corresponding rotations about these axes are represented by internal-external rotation, flexion-extension, and abduction-adduction, respectively. Researchers and clinicians use the anatomic coordinate system whenever possible because it is the most clinically relevant for diagnosis and treatment.
Degrees of freedom are the total number of independent movements needed to completely describe the position and orientation of a body in a given coordinate system. The musculoskeletal system has numerous degrees of freedom through which countless movements are accomplished. These movements can be performed in three-dimensional space through a set of translations and rotations and are typically described in an anatomic coordinate system. For example, the glenohumeral joint has a total of six degrees of freedom: three translations (superior-inferior, medial-lateral, and anterior-posterior), and three rotations (internal-external, abduction-adduction, and flexion-extension). However, depending on the analysis, the glenohumeral joint can be assumed to be a ball-and-socket joint, thus reducing the number of degrees of freedom to three rotations by constraining the translations. Similarly, the elbow only allows for one degree of freedom when it is considered a simple hinge joint.
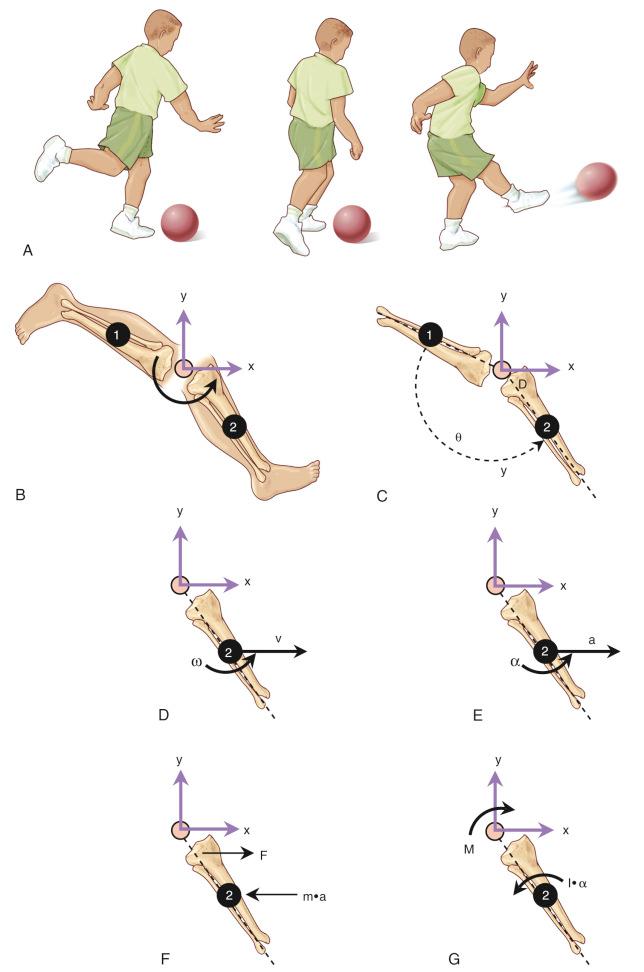
Degrees of freedom are important to consider when describing body motion and position numerically. Joint motion may be constrained by the shape of the articular surfaces or by stabilizing ligaments, reducing the degrees of freedom and simplifying the description. However, some joints, such as the knee and ankle, also allow for small amounts of translation that are important to consider when interpreting a clinical examination. With an anterior cruciate ligament (ACL) injury, the knee will have an increased level of anterior translation, thereby altering the anterior degree of freedom. Using reduced degrees of freedom is strategic when modeling or characterizing joints of the body. For example, when a person picks up an object from the floor and subsequently returns to an erect posture, each vertebra moves in three-dimensional space to achieve the desired posture, representing a large number of degrees of freedom. To evaluate lower back injuries using modeling techniques, the degrees of freedom can be significantly reduced by only considering the L5–S1 joint and assuming that the motion occurs only in the sagittal plane, resulting in a two-dimensional analysis. Similarly, in assessing the tibiofemoral joint during a kicking motion, it could be assumed that the tibia moves in only two dimensions within the sagittal plane ( Fig. 2.1A ). These reductive assumptions often overestimate the translations, rotations, forces, and moments required to perform the motion.
Three basic rules of physics—Newton's laws of motion—are used to describe the relationship between the forces applied to the body and the consequences of those forces on human motion ( Table 2.2 ).
| Law | Definition | Equation |
|---|---|---|
| First (inertia) | An object at rest tends to stay at rest and an object in motion tends to stay in motion with the same speed and in the same direction unless acted upon by an external unbalanced force. | |
| Second (acceleration) | The rate of change of the moment of a body is directly proportional to the applied force and takes place in the direction in which the force acts. | |
| Third (action-reaction) | For every action there is an equal but opposite reaction. |
Newton's first law states that an object at rest tends to stay at rest and an object in motion tends to stay in motion with the same speed and in the same direction (velocity) unless acted upon by an unbalanced force. This law is also commonly referred to as the law of inertia . Therefore a nonzero resultant force must act on a rigid body to change its velocity. For example, headrests are placed in cars to prevent whiplash injuries during rear-end collisions by stopping the motion of the head, which illustrates decreasing linear velocity and acceleration by application of an unbalanced force. Furthermore, if the resultant moments and forces are zero, then the body will also have no rotational or linear acceleration.
Newton's second law pertains to the behavior of objects for which all forces are not balanced. Therefore the resultant force is not equal to zero, and acceleration in the direction of the applied force will occur. The magnitude of the acceleration is proportional to the magnitude of the resultant forces or moments applied to the body. Thus, in essence, the first law is a special case of the second law:
where “F” is the resultant force, “m” is the mass of the body being acted upon, “a” is the acceleration of the body due to the unbalanced external forces, “M” is the resultant moment, “I” is the mass moment of inertia (resistance of a body to rotation), and α is the angular acceleration.
Linear acceleration can exist as an extremity is sent through a range of motion (ROM) during a task (see Fig. 2.1F ). In sports, an athlete frequently controls his or her mass moment of inertia or center of mass of the entire body by altering the positioning of the individual body segments to achieve stability or a particular motion. Gymnasts and divers use this concept to achieve multiple somersaults while in the air by tucking in the head and limbs closer to the center of the body, which is an example of angular acceleration due to changes in angular inertia (see Fig. 2.1G ).
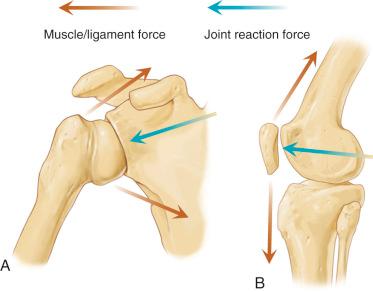
Newton's third law states that for every action there is an equal but opposite reaction. This law explains the idea that if a person pushes against a wall, it will in essence push back. Forces of action and reaction are equal in magnitude, but in the opposite direction. This concept is important in examining the principle of equilibrium and when using tools that assess forces being applied to the body of interest. Reaction forces act to constrain motions by reacting to an applied force. A daily application of this concept is simple walking and running. Every time a person places a foot on the ground, a force is exerted from the foot on the ground throughout the gait cycle. Simultaneously, however, a force of equal magnitude is exerted in the opposite direction from the ground up to the foot, which is termed a ground reaction force . Ground reaction forces are the forces applied by the ground because of the weight of the body. Similarly, within joints, muscles and connective tissues are found that create a joint reaction force ( Fig. 2.2 ). Both passive and active stabilizers maintain the humeral head within the glenoid fossa of the glenohumeral joint, which has implications for surgical repair of Bankart lesions by changing the arc of the glenoid and tendon transfers in changing the line of muscle action. If these joint structure changes alter the natural forces and/or the direction of these forces, joint instability would result, potentially leading to long-term degenerative changes.
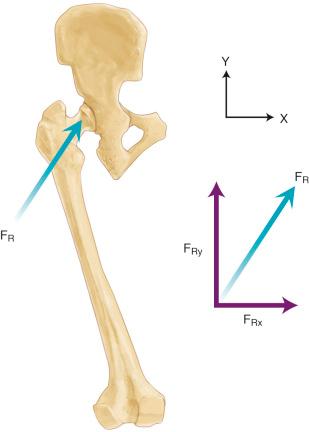
When a body is balanced by equal but opposite reactions for every action, the system is considered to be in a condition of equilibrium, which means that the net effect of the applied forces is zero as well as the net moment about any point. Although the sum of the force and moment vectors is zero, the body may still be moving at a constant velocity. Assuming a state of static equilibrium with a set of known force vectors, it is possible to determine unknown forces within a system. To do so, each force vector can be resolved into its individual components, such as the vertical (Fy) and horizontal (Fx) components for a two-dimensional coordinate system ( Figs. 2.3 and 2.4D ). Therefore the resulting equations for force and moment equilibrium in three dimensions are:
For static equilibrium, no linear or rotational motion occurs.
Using the aforementioned equations of static equilibrium, static analyses evaluate the external effects of forces on a rigid body at rest or during motion with a constant velocity. Applied to the body, static analyses are used to further determine the magnitude and direction of forces at joints and in the muscles. Forces provide both mobility and stability to the body but also introduce the potential to deform and injure the body. Typically, healthy tissues are able to withstand changes in their shape, but a tissue structure that has been injured by disease or trauma may not be able to adequately sustain the same loads required to perform activities of daily living. To perform static analyses, we must be able to represent the complex interactions of forces and moments acting on a body through the use of vectors and free-body diagrams.
The most common vector quantity in mechanical systems is a force. A force is applied on an object to create either a pushing or pulling response. Depending on the original state of the object, a force can cause a stationary object to move or alter the state of an object already in motion. Such forces can be either internal or external. Internal forces include those that hold a rigid body together, such as muscle tension generated within an extremity, whereas external forces are those applied to a rigid body. An example of an external force is the weight of an object being held in a person's hand. Forces can be further categorized into two subgroups: contact (tension, friction, external, and internal) and distance (gravitational and magnetic) forces. Distance forces act at a distance from the object or body with no direct physical contact. Additionally, forces can contain components acting in both the normal (perpendicular) and tangential (parallel) directions of the surface to which they are being applied.
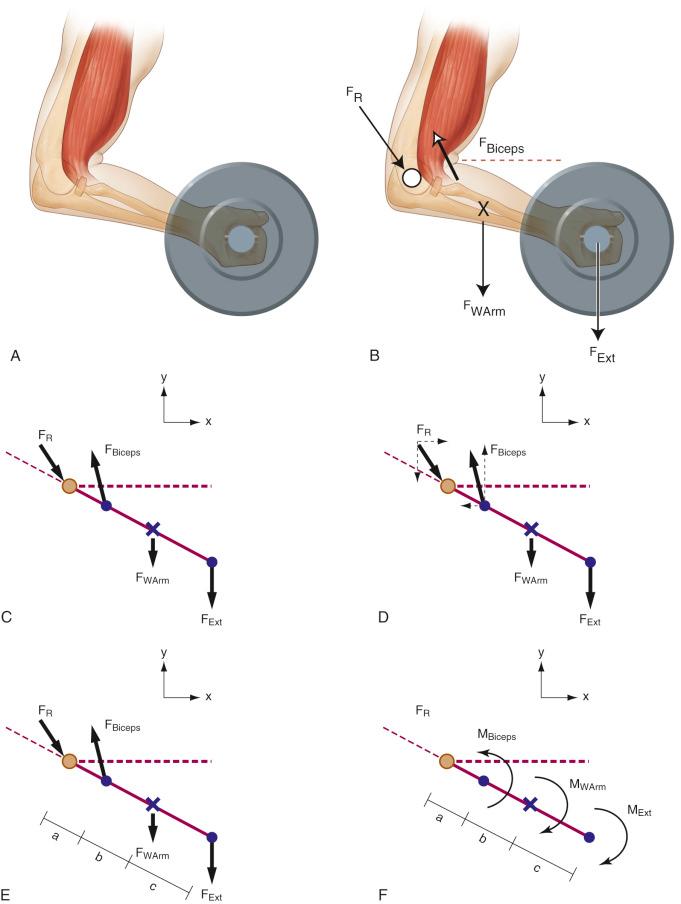
Vector quantities can represent not only translational motions in response to an applied force but also the rotation, twisting, and bending of an object. A moment (or torque) is determined by the magnitude of the force acting about a point and the length of the shortest distance between the point and line of action of the force. This distance is known as the moment or lever arm . A larger moment arm requires less force to achieve equivalent angular motion about the axis of rotation, which means that if the force remains the same but the lever arm increases, the moment will be of greater magnitude. Although a moment can realistically be calculated about any point, typically it is calculated about a joint axis of rotation during biomechanical analyses. For example, when tension is generated in the biceps muscle during a biceps curl exercise, the tendon pulls on the forearm at a distance from the elbow axis of rotation (see Fig. 2.4 ). This tension from the biceps muscle generates a positive moment about the elbow that can either help maintain the posture of the elbow or increase the amount of flexion, depending on whether the biceps muscle force is equal to or greater than the applied external forces of the weight.
To better evaluate a biomechanical system, such as forces being applied to a specified part of the body, free-body diagrams are an effective tool to simplify a complex analysis. Free-body diagrams allow for visualization and ease of calculation by properly identifying all the forces and moments acting on the body of interest in order to successfully achieve equilibrium. These diagrams are used by first drawing the body of interest and then isolating the body from its environment, only including the forces acting on the body. Again using the example of a biceps curl exercise to evaluate the elbow joint, the system should be drawn as only the forearm (with the radius and ulna combined as one), because this segment is the body segment of interest, with the elbow as the axis of rotation (see Fig. 2.4B ). It is important to note the position and orientation of the object by defining a coordinate system.
Applied forces are then identified and considered. Arrows representing the force vectors are drawn at every point where two (or more) bodies interact or join (see Fig. 2.4C ). Recalling that internal forces are those that hold a rigid body together, two examples within the human body are muscle contractions and bony contact at a joint line. Internal forces are further examined with the concept of stress, which is introduced in a later section of the chapter. External forces can be the weight of an object, friction, or gravity applied at the center of mass of a body segment. In a simplified situation, flexion of the elbow is counteracted by the weight of the forearm itself and the weight of the dumbbell. The point of application of the forearm weight is at the segment's center of gravity. Commonly this point is determined from anthropometric data. The point of application of the biceps force on the forearm is its tendon insertion. The remaining force is the result of contact with the distal end of the humerus and the proximal end of the forearm, whereby the point of contact is approximately at the joint surface of the bones. These forces can then be further resolved into their respective components along the previously identified x- and y-axes (see Fig. 2.4D ).
In addition to forces, the forearm experiences various applied moments. Because the points of application for the forces are known, the distances of each force along the forearm from the axis of rotation—the elbow—is also known (see Fig. 2.4E ). Using these distances as moment arm values, the next step is to identify moments created by each force. The direction of the moment is relative to the applied force and its relationship to the axis of rotation. No moments are generated by the forces at the elbow because their moment arms are zero (see Fig. 2.4F ). Once all the forces and moments applied to the body or body segment of interest are identified, they can be summed to determine the resultant force and moment. When the body is in a state of static equilibrium, the resultant forces and moments sum to zero, according to Newton's third law of motion.
These concepts of static analyses can be applied not only to whole-body analyses but also at the joint and tissue level. For the typical joint, forces can be related to compression and shear. For example, when a person is standing with the knee in full extension, the tibial plateau and femoral condyles experience compressive forces in the normal direction to each articular surface. However, an increased shear force is experienced during an anterior drawer test or when stopping quickly in a sporting event. Shear forces are experienced in the tangential direction along the tibial plateau. These forces are not only experienced between the bony structures but also transmitted through the soft tissue structures. During an anterior drawer test or quick stop, the ACL can become significantly loaded to resist anterior tibial translation and provide stability at the joint. The ACL becomes loaded as a result of a generated tensile force within the ligament to maintain equilibrium. However, after an injury such as an ACL rupture, opposing shear forces cannot be transferred through the ligament, and thus equilibrium cannot be maintained at the joint without excessive translation, resulting in anterior instability.
Based on the equations from Newton's second law of motion, dynamic analyses evaluate bodies in motion and can be divided into two subgroups: kinematics and kinetics. For dynamic systems, the forces and moments do not have a net value of zero, which violates the principle of equilibrium, and thus a different approach must be taken. Kinematics simply describes the motion of bodies, without regard to the factors that cause or affect the motion, by characterizing the geometric and time-dependent aspects of the motion. Conversely, kinetics is based on kinematics but includes the effects of forces and moments. Motion analyses and sports mechanics typically involve dynamic systems.
Simply stated, kinematics deals with motions without regard to forces and moments. These motions include translations and rotations. Translations are simply the linear motions in which all the parts of a rigid body move simultaneously in the same direction as every other point in that body and at the same velocity. Rotations are the angular motions of a rigid body along a circular path and about an axis of rotation. During passive knee flexion, the tibiofemoral joint undergoes both linear and angular motions. As the knee progresses through the ROM, the tibia experiences rotation in the sagittal plane, and simultaneously, the point of contact between the tibial and femoral articular surfaces translates in the posterior direction. Although flexion is the primary angular motion, internal tibial rotation also occurs, which exemplifies the complex motion that can occur at a single joint.
The spatial components used to describe linear kinematics are position, distance, and displacement. Position is a vector that simply defines the location of the object in space relative to a reference frame, commonly the center of a joint or a point of contact. Once the initial position changes, the object has moved a specified distance and displacement. Distance is a scalar quantity that describes the length of the entire path traversed. Displacement is a vector quantity (d) defining the shortest distance (straight line) between the starting and ending positions of the object independent of the path taken (see Fig. 2.1C ). Additionally, temporal descriptions of linear kinematics are speed, velocity, and acceleration. Velocity is a vector quantity (v) describing the rate of change of the position with respect to time, whereas speed is a scalar quantity equal to the magnitude of the velocity vector (see Fig. 2.1D ). Furthermore, acceleration is also a vector quantity (a) that describes the rate of change of velocity with respect to time, but it is commonly used to express an increase or decrease in speed (see Fig. 2.1E ).
Angular kinematics is experienced when a change in angular position occurs such that the body undergoes rotational motion about an axis of rotation. The angular distance through which the body moves is equal to the length of the angular path. Angular kinematics can describe rotatory motion for a body segment, such as the lower leg during a kick (see Fig. 2.1A ), in addition to the body as a whole, such as for a gymnast swinging on the bar to perform a giant circle. Descriptors used for these motions with respect to time are angular position, displacement, distance, velocity, and acceleration . These terms are similar to those used for linear kinematics, but they apply to a rotatory motion (see Fig. 2.1C–E ). The lower leg undergoes large changes in angular velocity (ω) and acceleration (α) throughout the ROM for activities such as running, swimming, or kicking a soccer ball. Most general movements in the body are a combination of both linear and angular motion. For example, during a normal gait cycle, the lower extremities translate and rotate. Similarly, during athletics, combined motions are clearly illustrated during pitching, as the glenohumeral joint creates an instantaneous axis of rotation when the ball is swung along an imaginary arc about the shoulder in addition to being propelled forward.
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here