Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Valvular diseases may be viewed as a model of how inappropriate loading conditions can lead to cardiac dysfunction, symptoms, and finally death. A paradox of valvular heart diseases is that, in contrast to diseases of myocardium, there is often discordance between normal left ventricular (LV) ejection fraction (EF) but decreased LV long axis function (quantified by LV global longitudinal strain [LV GLS]). Thus, to understand the role of strain in valvular diseases, one needs to understand the way the changes in loading conditions, LV geometry, and myocardial structure affect the myocardial deformation (i.e., strain), often without affecting EF.
The topic of how myocardial deformation is quantified is covered in Chapter 1 . In brief, myocardial deformation is a general term for changes that occur during contraction of the heart. In clinical practice, deformation is quantified via its three normal components: longitudinal, circumferential, and radial strain. Whereas in engineering the total solid-body deformation is quantified by also measuring the three sheer strain components, sheer in clinical practice is usually neglected or only indirectly quantified by a single measure of torsion. Strain is a local phenomenon; however, in clinical practice, it is usually expressed as a single global number as an average of local (segmental) processes. Strain can be measured anywhere, including nonmuscular structures (i.e., valves, aorta); however, the text focuses on LV GLS and, to a much lesser extent, right ventricular (RV) free wall strain (RVFWS) and RV GLS.
Aortic stenosis (AS) is a typical disease of pressure overload that over time results in a concentric increase in LV mass. The hemodynamics of it are characterized by high systolic stress and near-normal diastolic stress. In this setting, LV mass increase is due to increases in myocyte diameter. Given increased systolic stress, some decrease in deformation parameters, such as strain, is expected. Longstanding AS also leads to progressive replacement fibrosis. In the final stages, there are LV dilatation, depression of LVEF, and death.
Mitral regurgitation (MR) is a typical disease of volume overload. In compensated MR, there is an increase in diastolic stress but normal or near-normal systolic strain. Expectedly, given high preload, it is characterized by preserved or even above-normal LVEF and preserved deformation parameters. Although LV mass increases in MR, it has less to do with increase in myocyte diameter and more with increase in myocyte length. Still, in the end, LV dilatation and drop in EF occur, followed by death.
Finally, the LV response to aortic regurgitation (AR) is a mixture of pressure and volume overload. With this, it falls in between the AS and MR as far as the changes in ejection parameters are concerned. Of note, AR is characterized by the largest LV size with the largest increase in LV mass of the valvular diseases. Again, it shares a final common pathway of continuous dilation, EF drop, and death.
Myocardial deformation is determined by myocardial structure. A certain specific configuration of cardiac myocytes should always produce a similar contribution of individual strain components to total deformation. Although total deformation may vary with inotropic state and loading conditions, relative contributions of different strain components in a healthy heart should be the same. Yet, in valvular diseases, this is not always apparent.
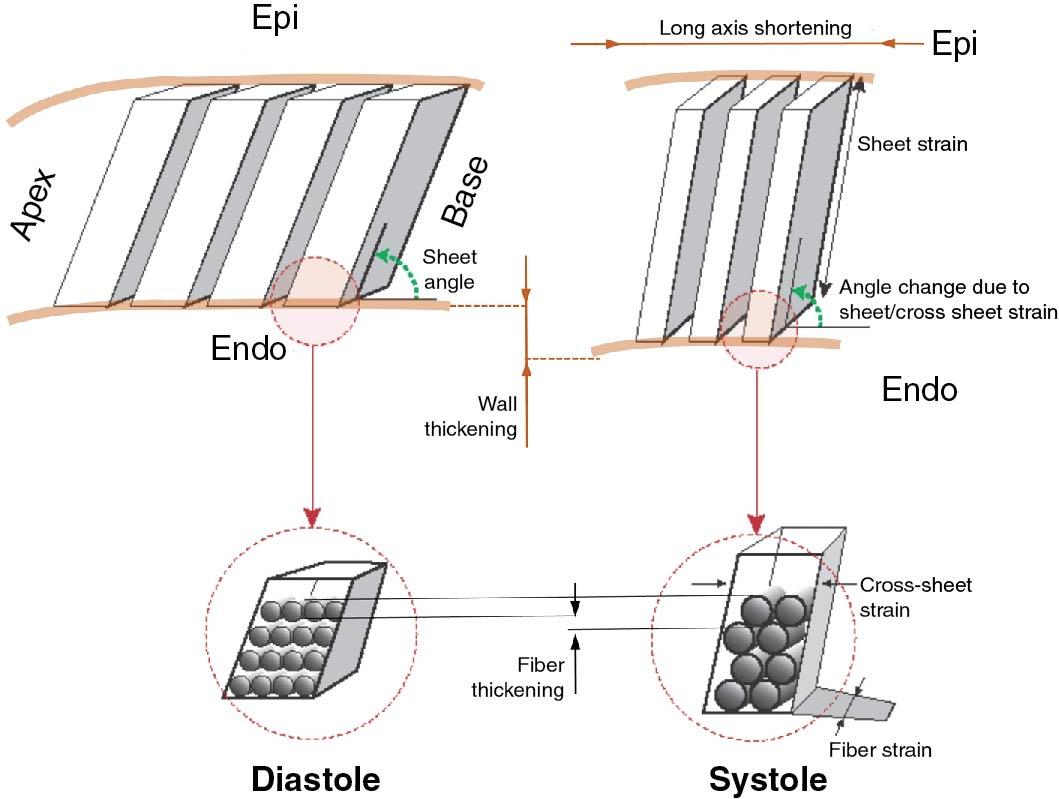
When cardiac myocytes contract, they deform by shortening their length in one direction while increasing their width in two other orthogonal directions. However, myocytes contract by a relatively minor amount of ∼15%, but the main purpose of contraction is an increase in wall thickness, typically in the range of 40%. To accomplish this, myocytes are organized in a complex secondary structure of muscle sheets. Individual myocytes lie in parallel, somewhat like logs in a firewood log rack, in approximately four myocyte-wide sheets that transverse from endocardium to epicardium ( Fig. 7.1 ). During systole, by changing the way myocytes are organized within the sheets, sheets augment individual myocyte shortening by becoming thinner and longer and increasing the sheet angle relative to endocardial surface during systole (see Fig. 7.1 ). These actions lead to muscle deformation that we can measure by three orthogonal normal strains (i.e., longitudinal, circumferential, and radial) and three sheer strains. Given (relative) muscle incompressibility and assuming low sheer, the three linear strains are interdependent so much so that we need to measure only two of the three normal strains to quantify deformation.
Classically, one talks about two types of overload—pressure and volume overload—although true loading conditions represent a mixture of the two, and in end-stage disease a very similar phenotype of systolic dysfunction, severe LV enlargement, and LV wall thinning emerges. Again classically, volume overload leads to eccentric LV hypertrophy (LVH; increased diastolic volume with unchanged relative wall thickness), whereas pressure overload leads to concentric LVH (no or small change in LV volume with increased relative wall thickness).
Experimental studies of pressure overload showed that, despite increase in thickness, there appears to be little change in myocardial structure. , This means that while individual myocytes are becoming thicker, transmural fiber orientation and their organization within sheets are unchanged.
Somewhat different and more complete data exist in volume-overloaded hearts. It seems that, with transition of LV diastolic geometry over time from normal to dilated, transmural fiber orientation remains the same. To accommodate the volume overload, there is an expected ∼15% increase in fiber length (due to myocyte elongation) and ∼20% sheet length (due to rearrangement of myocytes), with little change in sheet thickness. This is associated with increase in LV short axis diameter and, to a smaller degree, long axis length. The later two changes lead to a more spherical ventricle.
The above-mentioned changes occur throughout the heart. In addition, in the base of the heart, there is an increase in wall thickness occurring due to sheet sheer: The sheets remodel and become more perpendicular to the LV surface. This is the most relevant remodeling change during LV dilatation. There is increased wall thickness that parallels increase in cross-sectional area and is likely necessary to counter higher wall stresses (Laplace’s law). The LV apex does not experience significant increase in wall thickness, which may be reflective of lower wall stresses in the apex.
When a volume-overloaded remodeled heart contracts, there is very little change in fiber, sheet, and cross-sheet strain compared with a control state. The major difference is increased sheet sheer strain, which facilitates LV wall thickening. So, in sum, an animal model of volume overload, even with signs of heart failure present, does not lead to decrease in LV strains, and at least some increase of one of the strain components can be expected.
The most widely used deformation parameter is LV GLS rather than circumferential or radial strain. The reasons for this are twofold: practical and physiologic. Compared to other components, it is very easy to obtain data necessary to calculate LV GLS, and LV GLS measurements are less noisy than circumferential and radial strain ones. The physiologic reason is that LV GLS is less linked to LVEF than other strain components. Thus, GLS may be abnormal in disease states such as hypertension even if LVEF and circumferential strain are within normal limits.
A recent, simple, and elegant analytic model by Stokke et al, based on the relationship between EF deformation (strain), and two changes that define two overload states (increase in wall thickness [i.e., pressure overload] and increase in LV diastolic volume [i.e., volume overload] ) explains the dissociation of LV GLS and LVEF ( Fig. 7.2 ). A simplification of this relationship is shown in equation 1, assuming muscle incompressibility, quantification of strain at the midwall, and with strain and EF shown as fractions instead of percent:
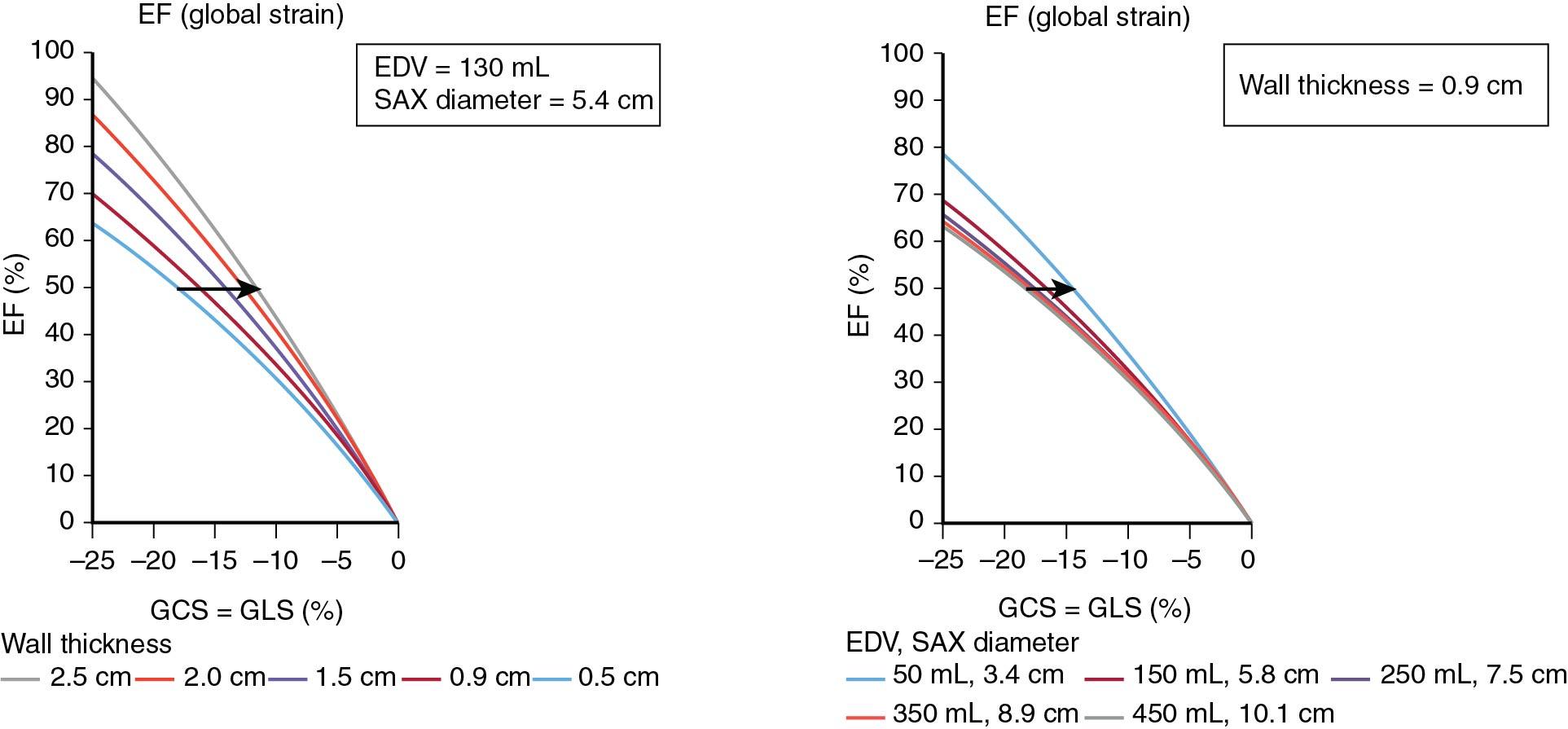
in which Scirc is circumferential strain, Slong is longitudinal strain, r is LV semiminor radius of the ventricle (i.e., one-half of end-diastolic diameter), and wall is wall thickness. Please note that longitudinal and circumferential strains must be entered as negative values. This relationship shows why GLS is more independent from LVEF than GCS and how small LV cavities with LVH are susceptible to impaired GLS in the presence of preserved EF ( Fig. 7.3 ).
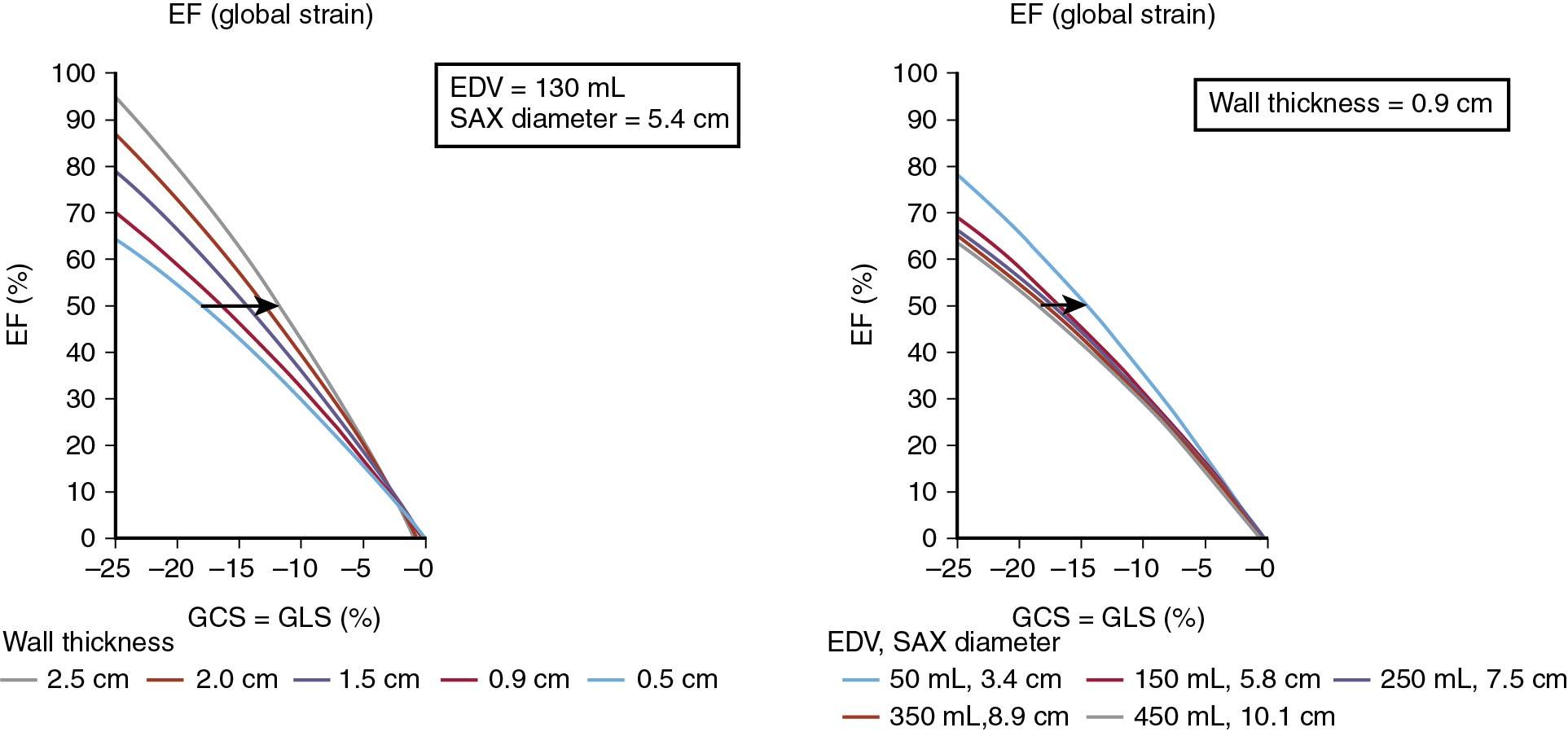
In the setting of valvular heart disease, the relationship means that if a healthy control is compared with patients with AS or MR with all three subjects having the same ejection fraction, an AS patient will have lower LV GLS and an MR patient would have higher LV GLS than a healthy control. In addition, a decrease in GLS could occur in both subjects without appreciative impact on EF.
As explained, pressure overload should decrease and volume overload should increase GLS. On the other hand, chronic overload conditions change myocardial structure: There are an increase in extracellular fibrosis, change in sarcomere titin isoforms, and increase in LV myocyte diameter. One could thus argue that we cannot claim that strain is “normal” unless one could measure it after suddenly and nontraumatically removing a culprit valvular lesion. Still, there are some data that can help us understand what one could consider normal in valve diseases.
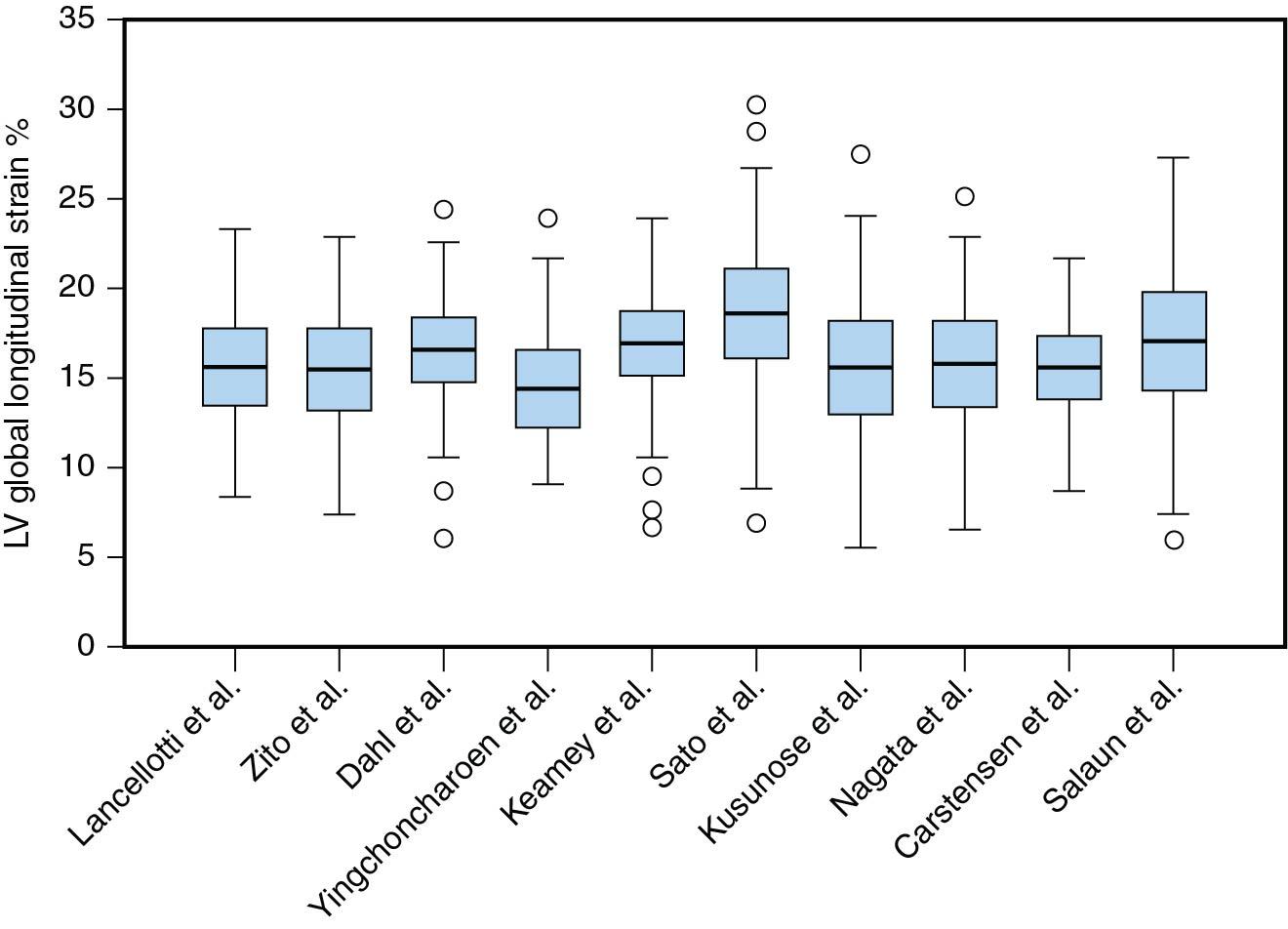
Table 7.1 shows GLS of the asymptomatic patients with valve diseases who have normal EF. As shown, the lowest values are encountered in AS while the highest ones are encountered in MR, with in-between values for AR. The question is, How do they compare to normal values? As discussed in Chapter 1 , normal strain values vary between different types of postprocessing software, but GLS worse than −16% is rarely normal, between −16% and −18% is borderline, and better than −18% is normal. Even with velocity vector imaging, an endocardial strain method used in many clinical studies because it is vendor-independent, mean values of −19.8% and −17.3% have been recorded. These findings are consistent with the initial conjecture that MR should increase strain, AS should decrease strain, with AR having strains that are slightly higher than normal.
| Disease Type | Patients ( n ) | Central Tendency Measure | Dispersion Measure | Author |
|---|---|---|---|---|
| Aortic stenosis | 1067 | −16.2% (mean) | 3.6 (SD) | Magne et al |
| Aortic stenosis | 504 | −16.1% (mean) | 4.0 (SD) | Hudded et al |
| Aortic regurgitation | 1063 | −19.5% (median) | −18.1 to −21.2 (25%-75% percentiles) | Alashi et al |
| Mitral regurgitation | 737 | −21.6 % (mean) | 2.0 (SD) | Mentias et al |
Although EF is widely used for decision making in valvular heart disease, it has important limitations. One can assess the usefulness of strain measurement in a particular valve disease by testing several independent hypotheses: Does strain predict exercise capacity? Does strain predict a future need for surgery? Does strain predict survival during conservative treatment or after surgery? Is it improved, unchanged, or worsened with treatment? And if it improves with treatment, does this improvement negate previous risk? Some of these hypotheses have been addressed and are summarized in the following sections, but much work remains to be done.
Strain is well described in AS. In a thoracic aortic banding (TAB) mouse model, which is a well-developed heart failure model with a hemodynamic profile that grossly mimics AS, there is an initial immediate drop in LVEF and circumferential and radial strain. It then decreases continuously over a follow-up period in a manner that reflects development of interstitial fibrosis and myocyte hypertrophy ( Fig. 7.4 ).
This model tells us something relevant about AS: that strain in AS is not fixed but can progressively decrease over time even though the hemodynamic insult (i.e., aortic narrowing) is constant. Although no animal data on GLS exist, the fact that both circumferential and radial strain decrease means that GLS also decreases.
Asymptomatic patients with AS normal systolic function (LVEF >50%) have the lowest GLS of all valve diseases ( Fig. 7.5 ), which is expected for several reasons.
First, the Stokke model links LVH (associated with AS) with normal EF to reduced GLS. In contrast, normal LVEF is closely linked to circumferential strain, which is also normal. Second, systolic strain is an ejection parameter and follows classic stress/strain relationships. The relationship of end-ejection systolic stress and LVEF in AS ( Fig. 7.6 ) shows higher wall stress to be associated with lower EF. In other words, given that AS, by definition, represents excess afterload, some drop in strain should be expected. Third, AS is associated with intrinsic changes in cardiac muscle properties. Figure 7.6 A shows that in AS, a significant proportion of patients have EF that is lower than what one would expect just because of afterload increase. This stems from additional histologic changes that occur in pressure overload, which include myocyte hypertrophy and interstitial fibrosis.
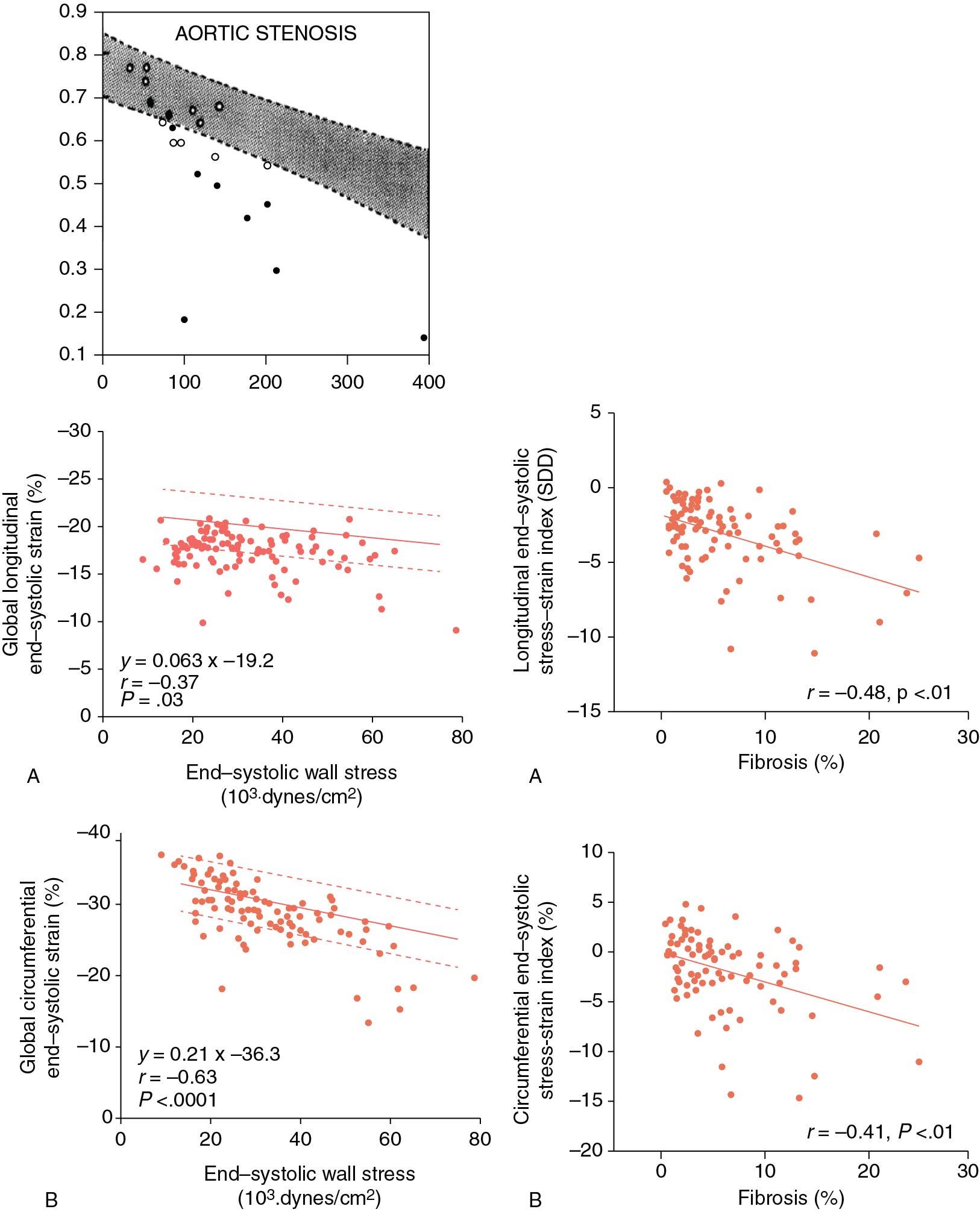
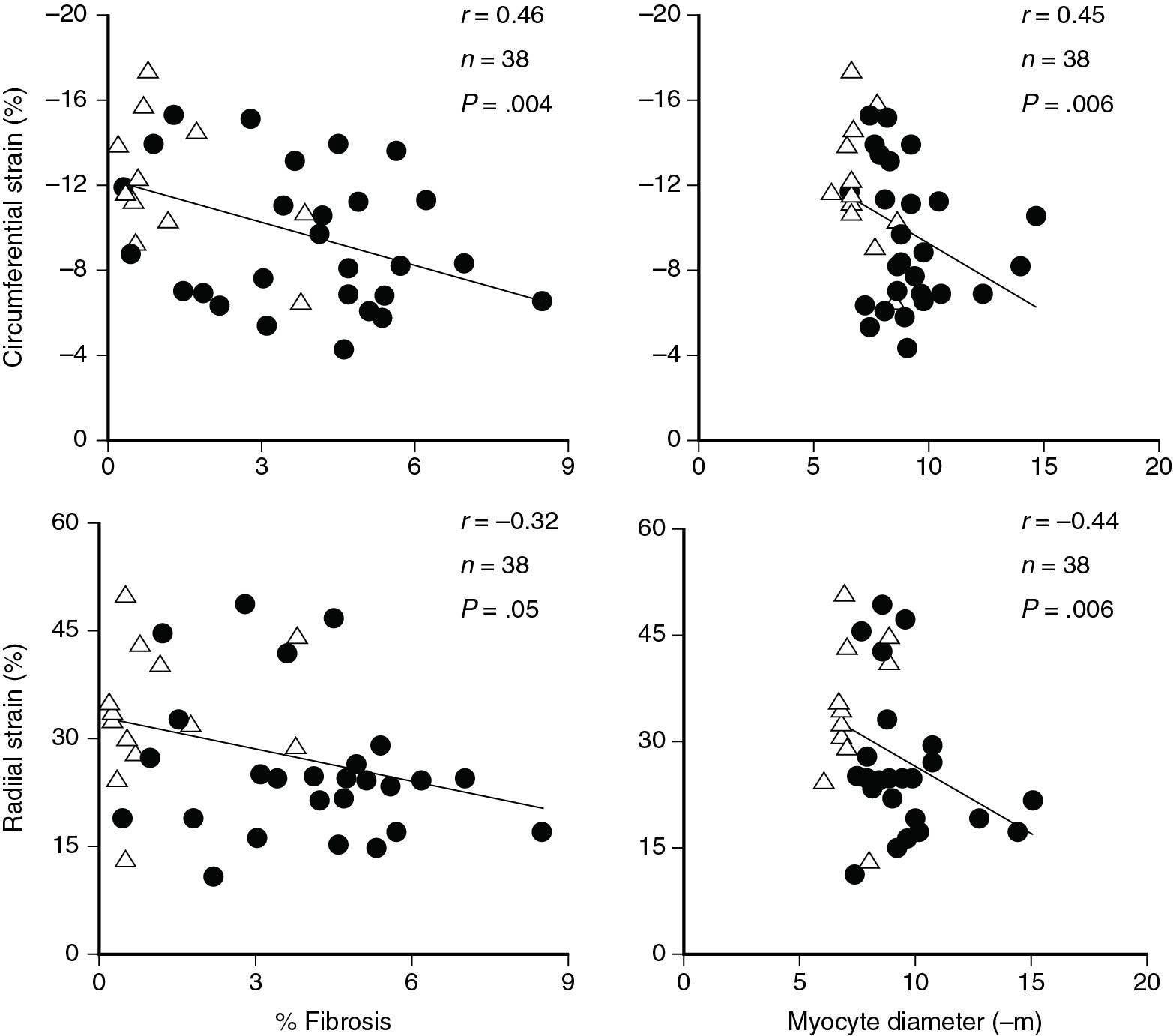
These factors were elegantly described by Slimani et al, who assessed intraoperative myocardial histology with stress strain relationships in 101 AS patients undergoing aortic valve replacement (AVR) (see Fig. 7.6 ). The authors have shown that predictably, higher end-systolic stress led to lower LV GLS and circumferential strain. However, even after correcting for afterload, both LV GLS and LV GCS remained at or below lower limits of normal. When stress-adjusted LV GLS and LV GCS were plotted against percent interstitial fibrosis, a clear inverse relationship emerged: In other words, and consistent with prior work, abnormal histology leads to excess decrease in both LV GLS and LV GCS that is uncovered after adjustment for end-systolic stress (ESS).
Slimani et al also support the Stokke model by showing that, when compared with healthy controls, LV GCS in AS patients undergoing AVR is normal (−29 ± 5% vs −30 ± 3% in healthy controls), while LV GLS is depressed (−17 ± 2% vs −20 ± 2% in healthy controls).
It follows that the severity of AS at least theoretically should inversely correlate with strain. A study by Ng et al shows that, indeed, the worse AS is, the lower the strain. In sum, in a clinical setting, strains are decreased in AS, with the decrease worsening the longer AS persists, and being worse in more severe AS.
The usefulness of GLS in predicting a need of AS surgery is unclear. A recent small study showed an association between surgery and GLS on univariate analysis but with a relatively small sample size. Patients with worse GLS in the basal segments had a greater probability of needing AVR in the future. Because impaired basal strain is a feature of amyloid heart disease, which is associated with AS, this may be an important confounder. Further studies are needed to elucidate these findings.
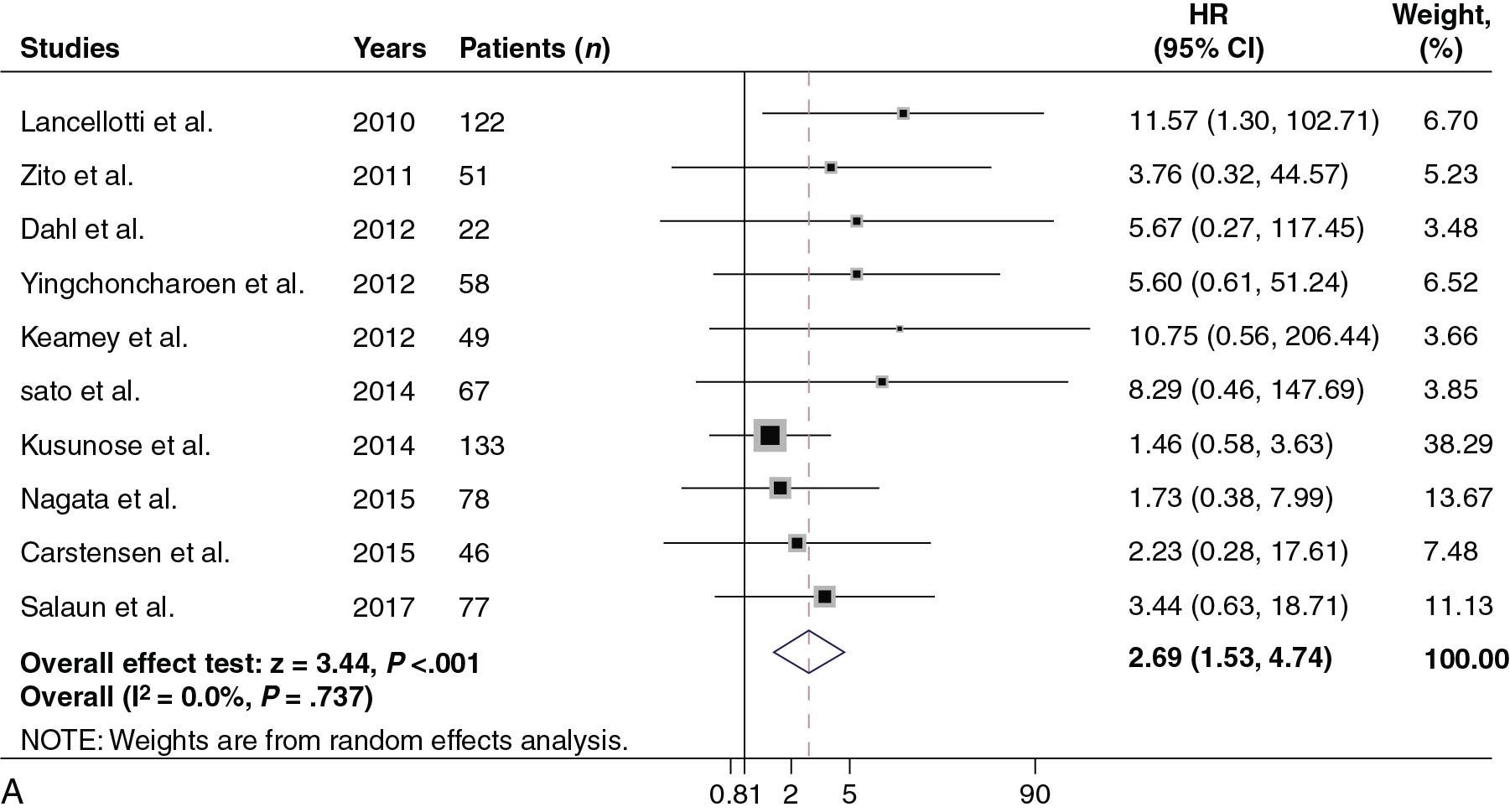
Strain in AS is clinically relevant because it predicts outcomes. In an already mentioned meta-analysis of asymptomatic AS patients with normal LVEF, strain was shown to be associated with survival after controlling for other clinical parameters ( Table 7.2 ). Similarly, Kusunose et al showed that in patients with moderate to severe AS and normal systolic function (LVEF >50%), GLS predicted outcomes independent not only of clinical factors but also of surgical correction. Studies have also shown that longitudinal strain is associated with survival when controlling, in addition, for brain natriuretic peptide (BNP), exercise capacity, and aortic valvuloarterial impedance. The relationship between survival and strain is nonlinear as it appears to steeply increase when GLS is worse than −17% ( Central Illustration ). In a recent individual patient meta-analysis, an optimal cutpoint of −14.7% was selected ( Fig. 7.7 A), and prognostic value was also witnessed in patients with EF ≥60% (see Fig. 7.7 B).
| Disease Type | Reference | n= | EF >50% | Asymtpomatic | Mean/Median | SD/25–75% Range | Hazard Ratio | 95% CI | Unit |
|---|---|---|---|---|---|---|---|---|---|
| Aortic stenosis | Magne et al | 1067 | y | y | −16.2% (mean) | 3.6 (SD) | 2.62 | 1.66-4.13 | Dichotomous at the cutoff of −14.7% |
| Aortic stenosis | Hudded et al | 504 | y | y | −16.1% (mean) | 4.0 (SD) | 1.12 | 1.07-1.16 | Per 1% increase |
| Aortic stenosis | Kusunose et al | 395 | y | n | −14.8% (median) | −12.1 to −17.2 (25–75%) | 1.05 | 1.03-1.07 | Per 1% increase |
| Aortic stenosis | Ng et al | 688 | n | n | −15.8% (mean) | 3.1 (SD) | 1.2 | 1.12-1.28 | Per 1% increase |
| Aortic regurgitation | Alashi et al | 1063 | y | y | −19.5% (median) | −18.1 to −21.2 (25–75%) | 1.11 | 1.04-1.19 | Per 1% increase |
| Mitral regurgitation | Mentias et al | 737 | y | y | −21.6 % (mean) | 2.0 (SD) | 1.6 | 1.47-1.73 | Per 1% increase |
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here