Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Predicting outcome is a time-honored duty of physicians, dating back at least to the time of Hippocrates. The need for a quantitative approach to outcome prediction, however, is more recent. Although a patient or family members will still want to hear a prognosis, there is increasing pressure to measure and publicly report medical care outcomes and assess the value of care. , deliver comparative information website ( www.leapfroggroup.org ). enacts penalties and provides incentives for providers based on quality. Public reporting of intensive care unit (ICU) performance, in the form of risk-adjusted mortality rates, is now mandated in some European countries and Veterans Administration (VA) hospitals in the United States and used in many ICUs in the United States. Thus clinicians need to understand the science behind these systems and how risk adjustment models may properly be applied. Risk adjustment systems allow performance (process of care) to be evaluated independent of the presenting condition (baseline risk).
Prognostication based on clinical observation is affected by heuristic bias, inaccurate estimation of the relative contribution of multiple factors, false beliefs, and human limitations such as fatigue. Outcome prediction models, on the other hand, will consistently replicate an estimate when considering relevant data. This presupposes that the model has been well developed and includes the most important predictive variables. Over time, we have learned that accepting patients in transfer, sociodemographic factors, and the point at which an outcome is assessed can lead to misinterpretation of supposedly objective measures. This chapter discusses what can (and should) be measured, how benchmarking models are created and assessed, how they are applied in clinical practice, how this information may be used, and the pitfalls and confounders associated with their use.
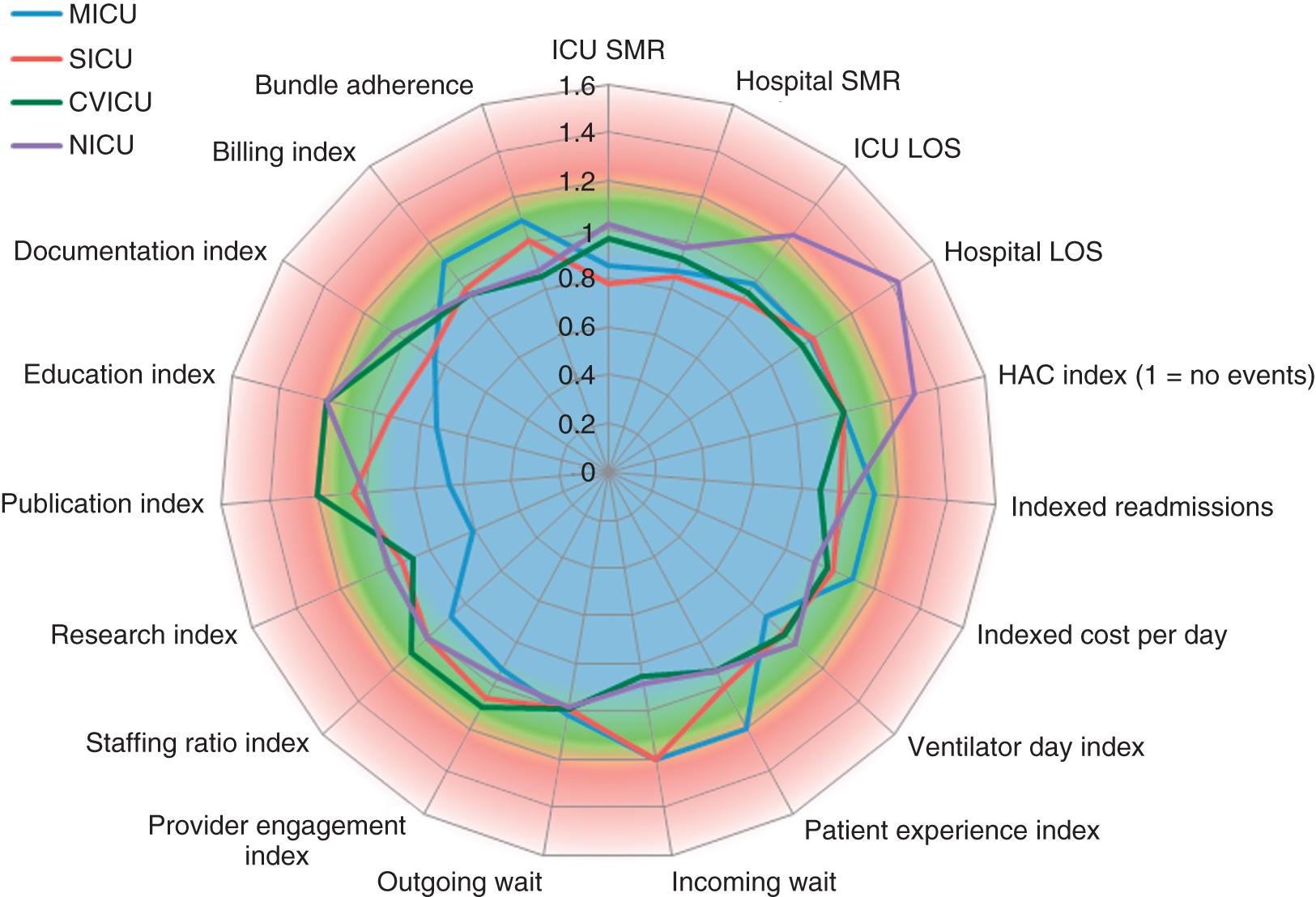
What is perceived as “quality” depends not only on individual subjective experience but also on integrating multiple perceptions and understanding the limitations of any one observation. Table 165.1 lists over 80 potential metrics categorized into process measures (what is done) or outcomes (what is achieved) in three categories: quality, efficiency, and patient/family experience. Process measures are important insofar as they provide guidance to interpreting outcomes that are out of range. A high urinary catheter utilization rate will affect the rate of catheter-associated urinary tract infections. Fig. 165.1 displays a “radar” plot where every variable has been normalized, such that 1.0 indicates performance at benchmark and the red-shaded areas indicate concern. In this hypothetical example, the neuro ICU appears to have issues with prolonged hospital length of stay (LOS), possibly related to hospital-acquired conditions. The medical ICU appears to excel at research, publication, and education, while having some issues with patient experience and wait times. Some metrics, such as mortality rate and LOS, will be determined primarily by a patient’s underlying physiology and health status. Thus rates are normalized using the ratio of observed to expected events and creating standardized rates.
| Process Measures | Quality Metrics | Efficiency | Experience | Optional (Local) |
|---|---|---|---|---|
| Daily wakeup/screen for weaning readiness | ICU SMR | ICU LOS | Patient satisfaction | Trainee performance |
| Glucose control | Hospital SMR | Hospital LOS | Family satisfaction | Publications |
| Lung protective ventilation (Vt/IBW) | 1-year SMR | ICU occupancy (95% CI) | Delirium rate | Funded research |
| Semirecumbent position (HOB at 30) | Sentinel events | Bed turnover rate | Tracheostomy rate | Local research |
| Stress ulcer prophylaxis | CNS events (CVA) | ED to ICU transfer time | % transfer to SNF | Regional transfers in |
| Mobilization of patients | Cardiac events (MI) | ICU to SD/floor time | Rehabilitation days | Workload (TISS) |
| Communication (daily goal transfer) | Respiratory events | Readmission to ICU | 1-year QOL/PICS | Organ donation rate |
| Antibiotic stewardship | Renal events (AKI) | Hospital readmission | Noise levels in ICU | Autopsy rate |
| Medicine reconciliation | GI events (GIB) | Cost/discharge | EOL care and DNR rate | |
| Handwashing | EMR (no cut/paste) | Cost/day | N:P staffing ratio | |
| DVT prophylaxis | DVT and HIT rates | Transfusion rates | MD:patient ratio | |
| Central line use and insertion | CLABSI rate | Ratio acute/LTAC days | Provider engagement | |
| Foley use and early removal | CAUTI rate | Palliative care referrals | Collaborative practice | |
| Ventilator and NIV utilization rates | VAP rate | Ventilator days | Procedure complications | |
| Assessing sedation RASS/CAMICU |
Designation as an ICU, 24-hour availability of consultants, an adverse event reporting system, routine multidisciplinary rounds, a standardized handover process, rate of catheter-related bloodstream infections, unplanned extubation rates, ICU readmission rate, and reporting and analysis of the standardized mortality rate (SMR) have been considered key indicators. The SMR is one of the most frequently used adjusted outcomes measured worldwide.
Mortality is a commonly chosen ICU and hospital outcome because it is unambiguous and readily available from a variety of data sources. Mortality, although clearly important, does not necessarily reflect quality of care or other important issues such as patient/family satisfaction, return to work, quality of life, or even cost, as early death results in a lower cost than prolonged hospitalization. There is a poor correlation between hospital rankings based on death and those based on other complications. A retrospective cohort study from 138 US ICUs contributing to Project IMPACT from 2001 to 2008 found that none of the 10 common performance indicators (e.g., mortality, readmission, LOS, bundle compliance) consistently correlated with the other 9. There is also little standardization on how mortality should be defined—traditional ICU or hospital rates are subject to discharge bias, but time-based outcomes (30-day, 1-year mortality rates) require intensive manual processes. Regionalized health information organizations or health information exchanges could make data collection easier but are not yet widely available.
Other potential outcomes of interest include morbidity, organ failure, complications, ICU or hospital LOS, ICU or hospital readmission, and health-related quality of life after hospital discharge. With electronic medical records (EMRs) and good coding, comorbidities may be identified by International Classification of Disease (ICD-9) and ICD-10 codes, but administrative records may not reflect all relevant events. ICU LOS is difficult to use as a proxy for quality of care because the frequency of distribution is usually skewed by long-stay outliers. In addition, early death shortens the LOS, resulting in competing risk effects. It is difficult to develop accurate models for ICU LOS at admission, and discrimination is usually inferior to that of mortality models based on the same database. A variety of regression methods have been applied to LOS prediction, with somewhat disappointing results. More success has been achieved by combining variables from ICU day 1 and day 5; variables with the most impact include mechanical ventilation, the PaO 2 :FiO 2 (arterial oxygen partial pressure/fraction of inspired oxygen) ratio, physiologic components, and day 5 sedation.
Patients readmitted to ICUs have increased hospital mortality and LOS. However, readmission rates are difficult to interpret without careful case-mix adjustment. Readmission rates are affected by triage decisions when ICU beds are constrained, but one study suggests that readmissions are only slightly higher with bed constraints, and, in any case, do not appear to affect short-term patient outcomes. In a retrospective study of 263,082 first-admission patients in 105 US hospitals, the median unit readmission rate was 5.9% (interquartile range [IQR], 5.1%–7.0%). Hospitals with high readmission rates, however, did not have higher standardized mortality rates or LOS after case-mix adjustment.
Patient satisfaction is an outcome highly valued by purchasers of health care, but it is subjective and requires substantial effort to quantify successfully. Evaluation of ICU performance requires a combination of indicators, but risk adjustment has mostly been developed for short-term mortality outcomes, with only a few studies risk-adjusting for other indicators.
The quality of a risk stratification system largely depends on the quality of the underlying database. Retrospective studies using existing data are quicker and less expensive but may be compromised by missing data, imprecise definitions, interobserver variability, and changes in medical practice over time. Data derived from discharge summaries or insurance claims do not always capture the presence of comorbid disease if the number of reportable events is truncated. Such coding bias is most apparent in severely ill patients. A variety of methods can assess the quality of the database, such as reabstraction of a sample of charts by personnel blinded to the initial results. Kappa analysis is a method for quantifying the rate of discrepancies between measurements (values) of the same variable in different databases (i.e., original and reabstracted). A kappa value of 0 represents random agreement and of +1.0 represents perfect agreement, but this statistic must be interpreted in light of the prevalence of the factor being abstracted.
Once data integrity is ensured, there are several possible approaches to relate outcome to the presenting condition. The empiric approach is to use a large database and subject the data to a series of statistical manipulations ( Box 165.1 ). Typically, death, one or more specific morbidities, and resource consumption (LOS) are chosen as outcomes (dependent variables). Factors (independent variables) thought to affect outcome are then evaluated against a specific outcome using univariate tests to establish the magnitude and significance of any relationship.
Precisely define outcome(s) of interest.
Identify and define candidate predictor variables (data analysis, expert opinion).
Collect data, and ensure its accuracy (reabstraction, kappa analysis).
Examine continuous variables, and transform or dichotomize as necessary.
Perform univariate analysis (chi-square, Fisher’s exact, Student’s t-test) against outcome(s).
Perform multivariate analysis (logistic regression, neural nets, Bayesian, others).
Examine and adjust for interactions among variables.
Develop a score or equation that relates independent variables to outcome.
Test calibration of model (goodness of fit, typically Hosmer-Lemeshow method).
Test discrimination of model (ROC area C-statistic, sensitivity, and specificity).
Validate model with independent data, split sample, or jackknife techniques.
Obtain external validation in new settings, and customize as needed.
Publish in peer-reviewed journal.
ICU-specific systems typically adjust for patient physiology, age, and chronic health condition. They may also assess admitting diagnosis, location before ICU admission or transfer status, cardiopulmonary resuscitation (CPR) before admission, surgical status, and mechanical ventilation use. An ideal approach would use only variables that characterize a patient’s initial condition, can be statistically and medically related to outcome, are easy to collect, and are independent of treatment decisions. There is also benefit to serial assessment of the condition, as the influence of independent variables may vary throughout the hospitalization. The Glasgow Coma Scale (GCS) is frequently used as a component of ICU severity scores but can be difficult to calculate correctly in sedated patients. The Full Outline of UnResponsiveness score, which includes information on brainstem reflexes and respiration, may be an alternative as a mortality predictor.
Measured variables such as “cardiac index” or “hematocrit” are preferred over “use of inotropes” or “transfusion given” because the criteria for intervention may vary. Widely used models rely on common measured physiologic variables (heart rate, blood pressure, and neurologic status) and laboratory values (serum creatinine level and white blood cell count). Models may consider age and chronic health status and include interaction terms when variables are not independent. Items chosen for inclusion in a scoring system should be readily available and relevant to involved clinicians. Specialized scoring systems become necessary for specific patient populations (pediatric, burn, trauma, cardiac surgery) whose underlying physiology or treatment course differs from that of the general adult ICU population. For example, left ventricular ejection fraction and reoperative status are important predictors of outcome in the cardiac surgical population but are neither routinely measured nor directly relevant to other population groups.
If the independent variable is dichotomous (yes/no, male/female), a two-by-two table can be constructed to examine the odds ratio and a chi-square test performed to assess significance ( Table 165.2 ). If multiple variables are being considered, the level of significance is generally set smaller than P = .05, using a multiple comparison correction.
| Predictor Variable: History of CHF | OUTCOME VARIABLE: MOF | |
|---|---|---|
| Yes | No | |
| Yes | 121 | 846 |
| No | 166 | 2697 |
* The odds ratio is defined by cross-multiplication (121 × 2697) ÷ (846 × 166). The odds ratio of 2.3 indicates patients with CHF are 2.3 times as likely to develop postoperative organ system failure as those without prior CHF. This univariate relationship can then be tested by chi-square for statistical significance.
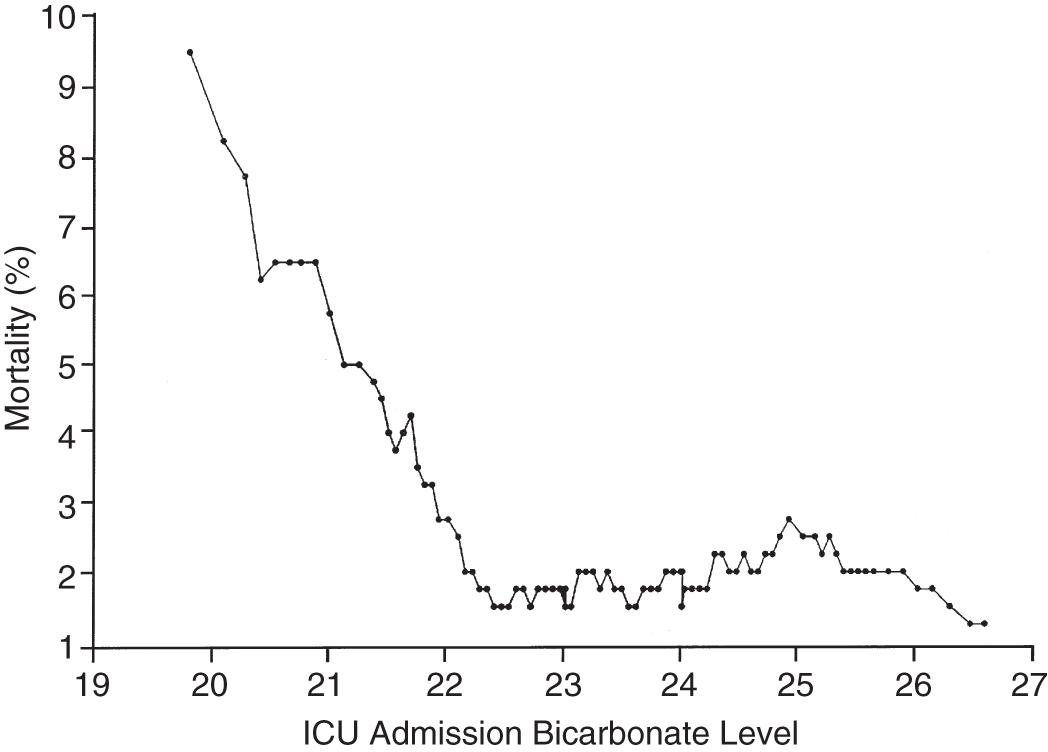
If the independent variable under consideration is continuous (e.g., age), a Student’s t-test is an appropriate choice for statistical comparison. With continuous variables, consideration must be given to whether the relationship of the variable to outcome is linear, exponential, or segmented across its range. Fig. 165.2 shows the relationship of ICU admission serum bicarbonate to mortality outcome in cardiac surgical patients ; data points have been averaged with adjacent values to produce a smoothed graph. Serum bicarbonate values higher than 22 mmol/L at ICU admission imply a relatively constant risk. Below this value, the risk of death rises sharply. Analysis of this locally weighted smoothing scatterplot graph suggests two ways for dealing with the impact of serum bicarbonate on mortality. One would be to make admission bicarbonate a dichotomous variable (i.e., >22 mmol/L or <22 mmol/L). The other would be to transform the data via a logarithmic equation to make the relationship more linear. Cubic splines analysis can be helpful when the relationship between independent and dependent variables is not linear or cannot be described by a simple transformation.
Univariate analysis assesses the forecasting ability of variables without regard to possible correlations or interactions between them. Linear discriminant and logistic regression techniques can evaluate and correct for overlapping influences on outcome. For example, both a history of heart failure and depressed left ventricular ejection fraction predict poor outcome in patients presenting for cardiac surgery. As might be expected, there is considerable overlap between the population with systolic heart failure and those with low ejection fraction. The multivariate analysis in this specific instance eliminates history of heart failure as a variable and retains only measured ejection fraction in the final equation to avoid double-counting of this general risk.
Because linear discriminant techniques require certain assumptions about data, logistic techniques are more commonly used. Multiple logistic regression produces an equation with a constant, a beta coefficient and standard error, and an odds ratio that represents each term’s effect on outcome. Table 165.3 displays the results of the logistic regression used in the Mortality Probability Model III ICU admission model (MPM 0 III). There are 17 variable terms, and a constant term, each with a beta value that, when multiplied by the presence or absence of a factor, becomes part of the calculation of mortality probability using a logistic regression equation. The odds ratios reflect the relative risk of mortality if a factor is present.
| Variable | Odds Ratios (95% Confidence Intervals) | Coefficients (Robust Standard Errors) |
|---|---|---|
| Constant | NA | −5.36283 (0.103) |
| Physiology | ||
| Coma/deep stupor (GCS 3 or 4) | 7.77* (5.921, 10.201) | 2.050514 (0.139) |
| Heart rate ≥150 bpm | 1.54 (1.357, 1.753) | 0.433188 (0.065) |
| Systolic BP ≤90 mm Hg | 4.27* (3.393, 5.367) | 1.451005 (0.117) |
| Chronic Diagnoses | ||
| Chronic renal insufficiency | 1.71 (1.580, 1.862) | 0.5395209 (0.042) |
| Cirrhosis | 7.93* (4.820, 13.048) | 2.070695 (0.254) |
| Metastatic neoplasm | 24.65* (15.970, 38.056) | 3.204902 (0.222) |
| Acute Diagnoses | ||
| Acute renal failure | 2.32 (2.137, 2.516) | 0.8412274 (0.042) |
| Cardiac dysrhythmia | 2.28* (1.537, 3.368) | 0.8219612 (0.200) |
| Cerebrovascular incident | 1.51 (1.366, 1.665) | 0.4107686 (0.051) |
| GI bleed | 0.85 (0.763, 0.942) | −0.165253 (0.054) |
| Intracranial mass effect | 6.39* (4.612, 8.864) | 1.855276 (0.166) |
| Other | ||
| Age (per year) | 1.04* (1.037, 1.041) | 0.0385582 (0.001) |
| CPR before admission | 4.47* (2.990, 6.681) | 1.497258 (0.205) |
| Mechanical ventilation within 1 hour of admission | 2.27* (2.154, 2.401) | 0.821648 (0.028) |
| Medical or unscheduled surgical admit | 2.48 (2.269, 2.719) | 0.9097936 (0.046) |
| Zero factors (no factors other than age from previous list) | 0.65 (0.551, 0.777) | −0.4243604 (0.088) |
| Full code | 0.45 (0.416, 0.489) | −0.7969783 (0.041) |
| Interaction Terms | ||
| Age × Coma/deep stupor | 0.99 (0.988, 0.997) | −0.0075284 (0.002) |
| Age × Systolic BP ≤90 | 0.99 (0.988, 0.995) | −0.0085197 (0.002) |
| Age × Cirrhosis | 0.98 (0.970, 0.986) | −0.0224333 (0.004) |
| Age × Metastatic neoplasm | 0.97 (0.961, 0.974) | −0.0330237 (0.003) |
| Age × Cardiac dysrhythmia | 0.99 (0.985, 0.995) | −0.0101286 (0.003) |
| Age × Intracranial mass effect | 0.98 (0.978, 0.988) | −0.0169215 (0.003) |
| Age × CPR before admission | 0.99 (0.983, 0.995) | −0.011214 (0.003) |
The challenge in building a model is to include sufficient terms to deliver reliable prediction while keeping the model from being cumbersome to use or too closely fitted to its unique development population. Generally accepted practice is to limit the number of terms in the logistic regression model to 10% of the number of patients having the outcome of interest to avoid “overfitting” the model to the developmental data set. It is important to identify interaction among variables that may be additive, subtractive (canceling), or synergistic and thus require additional terms in the final model. In the earlier example, seven interaction items were added to reflect important observations in elderly patients, where the very old without significant comorbidity frequently have better outcomes than unhealthy younger individuals.
The patient’s diagnosis is an important determinant of outcome, but conflicting philosophies exist on how disease status should be addressed by a severity adjustment model. One approach is to define principal diagnostic categories and add a weighted term to the logistic regression equation for each illness. This acknowledges the different impact of physiologic derangement by diagnosis. For example, patients with diabetic ketoacidosis have markedly altered physiology but a low expected mortality; a patient with an expanding abdominal aneurysm, conversely, may show little physiologic abnormality and yet be at high risk for death. Too many diagnostic categories, however, may result in too few patients in each category to allow statistical analysis for a typical ICU, and such systems are difficult to use without sophisticated (and often proprietary) software.
The other approach is to ignore disease status and assume that factors such as age, chronic illness, and altered physiology will suffice to explain outcome in large groups of patients. This method reduces manual data collection and avoids issues with inaccurate labeling of illness in patients with multiple problems and the need for lengthy lists of coefficients but could result in a model that is less accurate and somewhat dependent on having an “average” case mix. Regardless of the specific approach, age and comorbidities (metastatic or hematologic cancer, immunosuppression, and cirrhosis) are given weight in nearly all ICU models to help account for the patient’s physiologic reserve or ability to recover from acute illness. Yet many influential variables (e.g., frailty in elders, mental illness, paraplegia) increase the risk of poor outcome but are seldom incorporated into models. For example, acutely intoxicated patients tend to have low in-hospital mortality but striking rates of long-term mortality, particularly when street drugs are the intoxicating agent. Do-not-resuscitate (DNR) orders are a strong confounder in mortality evaluations but have only been included as a scoring variable in more recent models.
Models may be validated on an independent data set or by using the development set with methods such as jackknife or bootstrap validation. Two criteria are essential in assessing model performance: calibration and discrimination. Calibration refers to how well the model tracks outcomes across its relevant range. A model may be very good at predicting good outcomes in healthy patients and poor outcomes in very sick patients yet unable to distinguish outcomes for patients in the middle range. The Hosmer-Lemeshow goodness-of-fit test assesses calibration by stratifying the data into categories (usually deciles) of risk. The number of patients with an observed outcome is compared with the number of predicted outcomes at each risk level. If the observed and expected outcomes are very close at each level across the range of the model, the sum of chi-squares will be low, indicating good calibration. The P value for the Hosmer-Lemeshow goodness-of-fit increases with better calibration and should be nonsignificant (i.e., >.05). Special precautions apply when using the Hosmer-Lemeshow tests with very large databases, where massive numbers can produce significance without clinical importance.
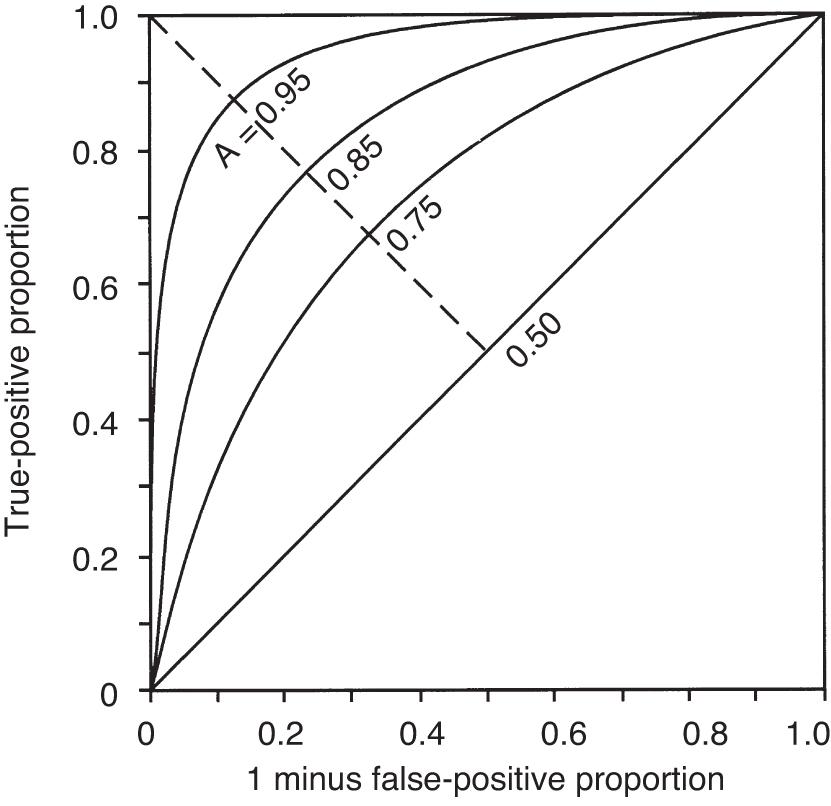
The second measurement of model performance is discrimination, or how well the model predicts the correct outcome. A classification table ( Table 165.4 ) displays four possible outcomes that define sensitivity and specificity of a model with a binary (died/survived) prediction and outcome. Sensitivity (the true-positive rate) and specificity (the true-negative rate, or 1 minus false-positive rate) are measures of discrimination but will vary according to the decision point chosen to distinguish among outcomes when a model produces a continuous range of possibilities. The sensitivity and specificity of a model when using 50% as the decision point will differ from that using 95% as the decision point. The classification table can be recalculated for a range of outcomes by choosing various decision points: for example, 10%, 25%, 50%, 75%, and 95% mortality risk. At each decision point, the true-positive rate (proportion of observed deaths predicted correctly), the false-negative rate (proportion of survivors incorrectly predicted to die), and overall correct classification rate can be presented. The C-statistic, or area under a receiver-operating characteristic (ROC) curve, is a convenient way to summarize sensitivity and specificity at all possible decision points. A graph of the true-positive proportion (sensitivity) against the false-positive proportion (1 minus specificity) across the range of the model produces the ROC curve ( Fig. 165.3 ). A model with equal probability of producing the correct or incorrect result (e.g., flipping a coin) will produce a straight line at a 45-degree angle that encompasses half of the area (0.5) under the curve. Models with better discrimination will incorporate increasingly more area under the curve to a theoretical maximum of 1.0. An area under the ROC curve (auROC) higher than 0.70 is acceptable, with higher than 0.80 considered excellent, and higher than 0.90 outstanding. Most ICU models have ROC areas of 0.8–0.9 in their development set, although the ROC area usually decreases when models are applied prospectively to new data sets. The ROC analysis is valid only if the model has first been shown to be well calibrated.
| Predicted Outcome | ACTUAL OUTCOME | |
|---|---|---|
| Died | Survived | |
| Died | a | c |
| Survived | b | d |
A model may discriminate and calibrate well on its development data set yet fail when applied to a new population. Discrepancies in performance can also relate to differences in surveillance strategies and definitions and can occur when a population is skewed by an unusual number of patients having certain risk factors, as could be seen in a specialized ICU. Large numbers of low-risk ICU admissions will result in poor predictive accuracy for the entire ICU population. The use of sampling techniques (i.e., choosing to collect data randomly on 50% of patients rather than all patients) also appears to bias results. Models deteriorate over time owing to changes in populations and medical practice. These explanations should be considered before concluding that quality of care is different between the original and later applications of a model.
Application of a severity of illness scoring system involves comparison of observed outcomes with those predicted by the model. The SMR is defined as observed mortality divided by expected mortality and is generally expressed as a mean value ±95% confidence intervals (CIs), which will depend on the number of patients in the sample. SMR values of 1.0 (± the CI) indicate that the mortality rate, adjusted for presenting illness, is at the expected level. SMR values significantly lower than 1.0 indicate performance better than expected. Small differences in scores, as could be caused by consistent errors in scoring elements, timing of data collection, or sampling rate, cause important changes in the SMR. , Different models applied to the same data set may produce discordant results, with the same hospital being identified as performing better than expected by one model and worse than expected by another.
Three widely used general-purpose ICU outcome systems are based on changes in patient physiology: the Acute Physiology and Chronic Health Evaluation (APACHE II, APACHE III, APACHE IV ), the Mortality Probability Models (MPM 0 -II, MPM 24 -II, MPM 0 -III), and the Simplified Acute Physiology Score (SAPS II, SAPS III , ). MPM 0 -II and SAPS II were developed from the same data set and initially shared variables. All models have been regularly updated and are in at least their third generation. Although variables and weighting differ, all are based on the premise that as critical illness increases, patients will exhibit greater deviation from physiologic normal for a variety of common parameters such as heart rate, blood pressure, neurologic status, and laboratory values. Risk is also assigned for advanced age and chronic illness. Variables from these models have also been incorporated into the US VA hospital system model (based on APACHE) and the California Outcomes Study (similar to MPM 0 -II and -III), in addition to models customized for international populations.
APACHE II was developed from data on 5815 adult medical and surgical ICU patients at 13 hospitals between 1979 and 1982; patients undergoing coronary artery bypass grafting, coronary care, or burn treatment were not part of the initial analysis. Severity of illness was assessed with 12 routine physiologic measurements plus the patient’s age and previous health status. Scoring was based on the most abnormal measurements during the first 24 hours in the ICU, with a maximum score of 71 points. The physiology score was then combined with coefficients to adjust the score for 29 nonoperative and 16 postoperative diagnostic categories, producing a mortality estimate.
APACHE II does not control for admission source or pre-ICU management, which could restore a patient’s altered physiology and lead to a lower score and thus underestimate a patient’s true risk. Mortality estimates are most accurate for patients admitted directly from the emergency department and less so for interhospital and intrahospital transfers. Failure to consider the location before ICU admission could thus lead to erroneous conclusions about the quality of medical care. Although the developers now consider APACHE II to have significant limitations based on its age, it is still in widespread use.
APACHE III, published in 1991, addressed limitations of APACHE II, including the impact of treatment time and location before ICU admission. The number of separate disease categories was increased from 45 to 78. APACHE III was developed on a representative database of 17,440 patients at 40 hospitals, including 14 tertiary facilities that volunteered for the study and 26 randomly chosen hospitals in the United States. APACHE III went through several partial updates between 1991 and 2003. Compared with APACHE II, the ranges of physiologic “normal” are narrower; deviations from normal are asymmetrically weighted to be more clinically relevant. Interactions between variables were considered, and five new variables (blood urea nitrogen, urine output, serum albumin, bilirubin, and glucose) were added, whereas the APACHE II variables serum potassium and bicarbonate were dropped. Information was also collected on 34 chronic health conditions, of which seven (AIDS, hepatic failure, lymphoma, solid tumor with metastasis, leukemia/multiple myeloma, immunocompromised state, and cirrhosis) were significant in predicting outcome. Customized models were developed for patient populations (e.g., cardiac surgery) excluded from APACHE II. Overall correct classification for APACHE III was much improved over the prior model, and for the first time sequential scoring was introduced to update the daily risk estimate. APACHE III scores were also correlated with predictions for ICU LOS, need for interventions, and nursing workload.
APACHE IV was published in 2006 with refinements to address the impact of sedation on GCS, expand the number of diagnostic groups, and add or rescale predictive variables ( Table 165.5 ). APACHE IV, based on a sample of 110,558 patients in the United States, has excellent discrimination (ROC area = 0.88) and impressive calibration (Hosmer-Lemeshow C-statistic 16.8, P = .08). Outcome assessment using the revised model differed substantially from prior versions. A hospital using APACHE III software in 2006, for example (calibrated to 1988–1989 results), might have congratulated themselves on a superb SMR of 0.799, whereas using APACHE IV would have revealed their SMR to be not different from the average at 0.997.
| Variable | Coefficient | Odds Ratio |
|---|---|---|
| Emergency surgery | 0.2491 | 1.28 |
| Unable to access GCS | 0.7858 | 2.19 |
| Ventilated on ICU day 1 | 0.2718 | 1.31 |
| Thrombolytic therapy for acute myocardial infarction | −0.5799 | 0.56 |
| Rescaled GCS (15-GCS) | 0.0391 | 1.04 |
| 15-GCS = 0 | 1.00 | |
| 15-GCS = 1, 2, 3 | 1.04–1.12 | |
| 15-GCS = 4, 5, 6 | 1.17–1.26 | |
| 15-GCS = 7, 8, 9 | 1.31–1.42 | |
| 15-GCS = 10, 11, 12 | 1.48–1.60 | |
| PaO 2 /FiO 2 ratio | −0.00040 | 1.00 |
| ≤200 | 1.00–0.92 | |
| 201–300 | 0.92–0.89 | |
| 301–400 | 0.89–0.85 | |
| 401–500 | 0.85–0.82 | |
| 501–600 | 0.82–0.79 | |
| Chronic health items | ||
| AIDS | 0.9581 | 2.61 |
| Cirrhosis | 0.8147 | 2.26 |
| Hepatic failure | 1.0374 | 2.82 |
| Immunosuppressed | 0.4356 | 1.55 |
| Lymphoma | 0.7435 | 2.10 |
| Myeloma | 0.9693 | 2.64 |
| Metastatic cancer | 1.0864 | 2.96 |
| Admission source | ||
| Floor | 0.0171 | 1.02 |
| Other hospital | 0.0221 | 1.02 |
| Operating/recovery room | −0.5838 | 0.56 |
APACHE IV relies on physiologic abnormalities to account for 66% of the model’s explanatory power. ICU admission diagnosis (using 116 categories) accounts for about 17%, with the remainder accounted for by age, chronic illness, location before admission, and interaction terms. There are limitations to the use of APACHE IV. First, the increased complexity of the model makes it impossible to use without dedicated software. The data entry burden, however, can be mitigated by porting data into APACHE from a hospital’s clinical information system. Second, APACHE IV was developed and validated in ICUs in the United States, and international differences in ICU resources, triage policies, models of care, and bed availability affect benchmarking performance in a new environment. The authors also stress that “prediction for an individual contains variance” and that “a prediction is only an approximate indicator of an individual’s probability of mortality.” As an example, they mention that the 95% CIs around a predicted mortality of 5% would typically be 3.9%–6.5% and that the absolute ranges of CIs widen as the predicted rate increases. APACHE IV has been recalibrated to APACHE IVa, and APACHE V is currently under development.
The original MPM was developed on 755 patients at a single hospital using multiple logistic regression to assign weights to variables predicting hospital mortality. The MPM-II models were developed on an international sample of 12,610 patients and then validated on a subsequent sample of 6514. A subscript (0, 24, 48, 72) designates time of the evaluation in approximate hours post admission. MPM-II, as with APACHE II, excluded pediatric, burn, coronary, and cardiac surgical patients and estimated hospital mortality risk based partly on physiologic derangement, using a smaller number of variables. However, MPM puts more weight on chronic illness, comorbidities, and age and less on acute physiologic derangement compared with APACHE. MPM models can use data obtained at ICU admission (MPM 0 ) and also at the end of the first 24-hour period (MPM 24 ), with the latter covering a time interval more comparable to APACHE. Whereas APACHE generates a score and then, with additional information, converts that score into a probability estimate of survival, MPM directly calculates a probability of survival from the available data. Because this involves a logistic regression equation, it is difficult to accomplish at bedside without a computer or programmable calculator.
The MPM 24 variables account for differences in patients who remain in the ICU for 24 hours or longer versus those who die early or recover rapidly. This line of reasoning has been further extended to create 48- and 72-hour models, although these have not yet been updated from MPM-II to MPM-III. Additional variables in MPM 24 , MPM 48 , and MPM 72 but not MPM 0 are prothrombin time, urine output, creatinine, arterial oxygenation, continuing coma or deep stupor, confirmed infection, mechanical ventilation, or intravenous vasoactive drug therapy. Probability of death increases at 48 and 72 hours even if the MPM variables and coefficients are unchanged, implying that mortality risk is increasing in patients whose clinical profile remains unchanged over time. The most important difference between MPM and APACHE is that the MPM 0 produces a probability estimate that is available at ICU presentation and is independent of ICU treatment. MPM also does not require specifying a diagnosis, which can be an advantage in complex ICU patients but may also make it more susceptible to error with changes in case mix and generates, on average, a lower auROC.
MPM 0 -II became the mortality benchmarking component for the Society of Critical Care Medicine’s (SCCM) Project IMPACT database launched in 1996. By 2002 it was apparent that mortality predictions based on mid-1980s results were outdated, and average SMRs in Project IMPACT hospitals had drifted to 0.85. MPM 0 -III was developed from a population of 124,855 patients in 135 ICUs at 98 Project IMPACT hospitals. Hospital mortality in this population was 13.8% versus 20.8% in the MPM 0 -II cohort. All of the 15 variables from MPM 0 -II remained associated with mortality, but the relative impact had changed. For example, gastrointestinal bleeding was no longer a serious risk factor, presumably because of advances in resuscitation, endoscopic procedures, treatment of Helicobacter pylori, and availability of proton pump inhibitors since the original study. Additionally, two new variables were added: “full code” resuscitation status at ICU admission and “zero factor” or absence of all MPM 0 -II risk factors except age. Seven age interaction terms were added to reflect the declining marginal contribution of acute and chronic medical conditions to mortality risk in the elderly. MPM 0 -III calibrated well (Hosmer-Lemeshow goodness-of-fit 11.62; P = .31) with an auROC of 0.823, similar to that of MPM 0 -II. Although the ROC area is lower than with APACHE, MPM users do not need to specify a diagnosis, which may be difficult in a complex patient with multiple problems. The simplicity of data collection and ability to generate a prognosis soon after arrival (rather than at 24 hours) are advantages.
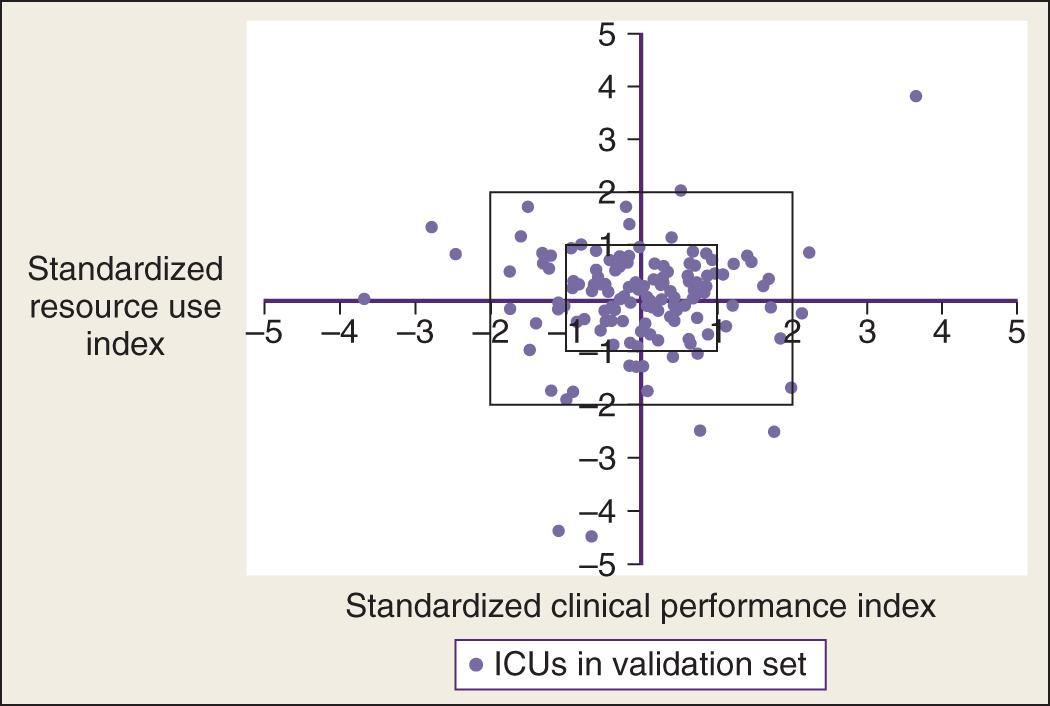
Limitations of the MPM 0 -III include lower discrimination and use of a self-selected population of Project IMPACT participants in North America. Although in theory, extreme case-mix differences might affect MPM performance, in practice, SMRs obtained using MPM 0 -III versus specially constructed subgroup models were nearly identical in the 135 ICUs studied, suggesting specialized subgroup models are not usually necessary. MPM 0 -III has been prospectively validated on an additional 55,459 patients at 103 adult ICUs in North America and calibrates well with more contemporary Project IMPACT hospitals (78 units participating in both studies plus 25 new participants). The Project IMPACT database was also used to update the resource utilization “Rapoport Teres” graph that plots severity-adjusted mortality versus severity-adjusted LOS ( Fig. 165.4 ).
The California Intensive Care Outcomes Projects (CALICO) was developed to produce public reports comparing outcomes for patients treated in California ICUs as part of the larger California Hospital Outcomes Project mandated by the state of California. After evaluating risk models available in the early 2000s, the California Healthcare Foundation and the National Quality Forum endorsed a modified and recalibrated version of the MPM 0 -II model termed “ICU Outcomes Model,” or ICOM mort , which has an auROC of 0.84 in prospective validation. The model includes 28 additional interaction terms and differs in patient exclusions from MPM-II and MPM-III. An additional model (ICOM LOS ) considers LOS. The CALICO project yielded several important findings, most notably that substantial (twofold) variation exists in mortality rates among hospitals, even after risk adjustment. Beginning in 2007, California required every ICU in the state to report severity-adjusted mortality rates. A recent study of 936,063 patients comparing the California experience with that of Arizona, Nevada, and Texas (which did not have public reporting requirements) concluded that while outcomes in California had improved, mortality rates also decreased in the control states.
SAPS II was developed on 13,152 patients at 137 adult medical or surgical ICUs in Europe and North America, sharing the MPM-II data set. Like MPM and APACHEII, SAPS excluded burn patients, patients younger than 18 years, coronary care patients, and cardiac surgery patients. The outcome measure for SAPS II was vital status at hospital discharge. Seventeen variables were used in the SAPS II model: 12 physiologic variables; age; type of admission; and the presence of AIDS, metastatic cancer, or hematologic malignancy.
Not surprisingly, the SAPS II model also drifted out of calibration over time. SAPS III, a multicenter, multinational study, collected data on 19,577 patients from 307 ICUs during the fall of 2002. When applied to this cohort, SAPS II underestimated hospital mortality, and although it discriminated well (ROC area, 0.83), calibration was poor, and model performance differed by geographic region. The final SAPS III model ( Box 165.2 ), created based on 16,784 patients using logistic regression methods, contains 20 variables and has good discrimination (ROC area 0.848) and calibration (Hosmer-Lemeshow C-statistic = 14.29; P = .16). Customized models were generated for seven worldwide regions to address geographic variation in population outcomes.
Age (in years)
Comorbidities: cancer, cancer therapy (scored separately), chronic heart failure (NYHA IV), hematologic cancer, cirrhosis, AIDS
Length of stay before intensive care unit (ICU) admission, days
Intrahospital location before ICU admission
Use of major therapeutic options before ICU admission (e.g., vasopressors)
ICU admission: planned or unplanned
Reason for ICU admission
Surgical status at ICU admission: emergency, elective, or none
Anatomic site of surgery
Acute infection at ICU admission
Lowest estimated Glasgow Coma Scale score (points)
Total bilirubin (highest)
Body temperature (highest)
Creatinine (highest)
Heart rate (highest)
Leukocytes (highest)
Hydrogen ion concentration (lowest pH)
Platelet count (lowest)
Systolic blood pressure (lowest)
Oxygenation (P/F ratio)
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here