Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Leg length inequality in children is a frequent parental concern or physical finding noted by the orthopaedist. It is commonly identified incidentally during screening examinations such as those performed on armed forces recruits, as well as during scoliosis screening and routine assessments of the asymptomatic adult population. , , The management of this deformity varies from no treatment to extensive multistage reconstruction to limb ablation and prosthetic fitting, a
a References , , , , , .
depending on the severity of the inequality and the function of the limb.
Unique aspects of the management of leg length inequality in children include the dynamics of lower limb growth and the need to estimate the projected discrepancy at skeletal maturity. These factors help determine the best orthopaedic management of the deformity and the surgeon’s ability to alter normal growth as a form of that management. To properly treat children with leg length inequality, the surgeon must be comfortable assessing leg length inequality clinically and radiographically, be cognizant of the various causes of leg length inequality, understand normal growth and the impact of abnormal growth on the individual’s limb, be able to chart and estimate ultimate leg length inequality in a skeletally immature child, know which modalities are available to normalize leg length inequality, and select the appropriate treatment for each patient.
Asymptomatic leg length inequality is relatively common in the healthy pediatric and adult populations. , , Soukka and colleagues found that 53 of 247 asymptomatic adults had a leg length inequality averaging 5 mm, with a maximum of 2 cm. Hellsing found a leg length inequality between 0.5 and 1.5 cm in 32% of 600 military recruits and an inequality that exceeded 1.5 cm in 4%. Rush and Steiner found equal leg lengths in only 23% of 1000 army recruits. Similarly, Walker and Dickson found that 138 of 5303 children (2.6%) aged 10 to 14 years who were screened for scoliosis had a pelvic tilt secondary to leg length inequality or pelvic asymmetry. Anderson and associates reported up to a 1- to 2-cm difference in length or circumference in the normal population.
In the past, limb length inequality was most commonly a residuum of poliomyelitis. With vaccination, this cause is now rare in the Western Hemisphere. The list of possible causes of leg length inequality in children is long ( Box 20.1 ), but in general, it can be classified as congenital, developmental, or acquired. Congenital causes include congenital femoral deficiency (including proximal femoral focal deficiency), fibular deficiency, tibial hemimelia, hemimyelomeningocele, idiopathic hemihypertrophy or hemiatrophy (anisomelia), and spinal dysraphism. Developmental causes, in which the discrepancy evolves with growth, include melorheostosis, congenital clubfoot deformity, enchondromatosis, osteochondromatosis, neurofibromatosis with gigantism, congenital pseudarthrosis of the tibia, and vascular anomalies such as Klippel-Trénaunay syndrome. Acquired causes include the following: physeal growth disturbance from fracture, infection, irradiation, or other causes such as infantile or adolescent Blount disease; Legg-Perthes disease; malunion of a long-bone fracture; growth stimulation secondary to a long-bone fracture; and inflammatory arthritis.
Congenital limb deficiency
Congenital femoral deficiency
Congenital fibular deficiency
Tibial hemimelia
Asymmetric neurologic disorders
Hemimyelomeningocele
Poliomyelitis
Asymmetric static encephalopathy (e.g., hemiparesis)
Asymmetric peripheral neuropathy
Trauma
Malunion
Physeal growth disturbance or arrest after fracture
Other acquired causes of physeal growth disturbance
Infection
Tumor
Enchondroma
Osteochondroma
Unicameral bone cyst
Irradiation
Infantile Blount disease
Adolescent Blount disease
Legg-Calvé-Perthes disease
Hemiatrophy
Idiopathic, nonsyndromic hemiatrophy
Russell-Silver syndrome
Unilateral clubfoot deformity
Congenital pseudarthrosis of the tibia
Posttraumatic overgrowth
Femoral shaft fracture
Tibial shaft fracture
Soft tissue overgrowth syndromes
Gigantism with neurofibromatosis
Klippel-Trénaunay syndrome
Beckwith-Wiedemann syndrome
Proteus syndrome
Idiopathic hemihypertrophy
Inflammatory arthritis
An important diagnostic category is idiopathic hemihypertrophy or hemiatrophy. Ballock and colleagues pointed out that hemihypertrophy can occur as part of a recognized clinical syndrome or in isolation (nonsyndromic). However, what constitutes hemihypertrophy or hemiatrophy is not clearly delineated except in severe situations. , Further, the distinction between normal variation between the two sides of the body and abnormal hypertrophy or atrophy is not clear; as mentioned earlier, a significant proportion of the “normal” population has a detectable leg length inequality. One variation of hemiatrophy is Russell-Silver syndrome, , which is characterized by short stature and associated hemiatrophy ( Fig. 20.1 ). The cause of idiopathic nonsyndromic hemihypertrophy is not known. The finding of cutaneous or vascular anomalies allows for specific diagnoses to be made. These include Proteus syndrome, Klippel-Trénaunay syndrome, neurofibromatosis, and Beckwith-Wiedemann syndrome. Both nonsyndromic hemihypertrophy and Beckwith-Wiedemann syndrome have been associated with the development of childhood neoplasias. b
b References , , , , , , , , , , , , , , , , , .
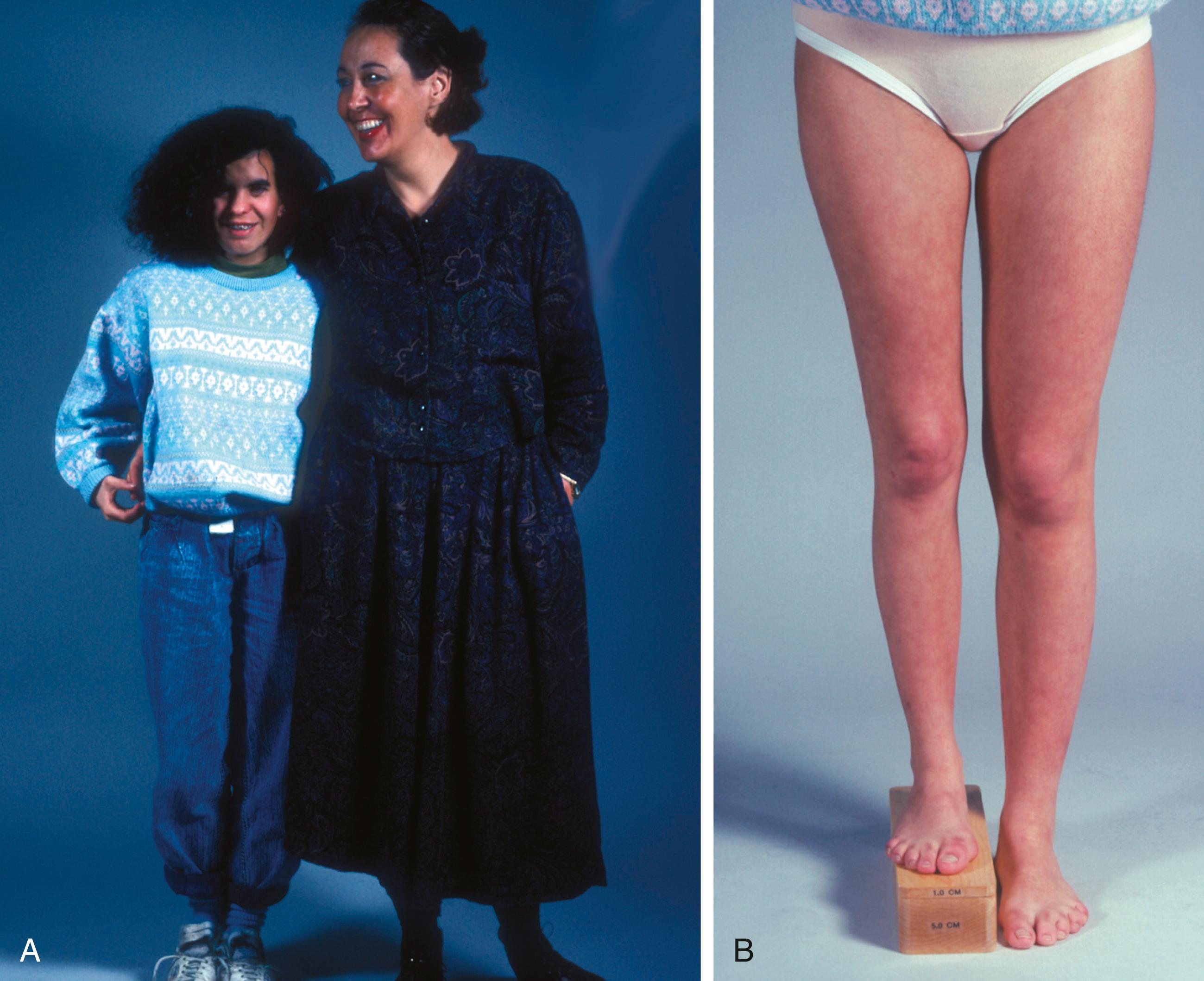
Beckwith-Wiedemann syndrome, described independently by Beckwith and Wiedemann, is characterized by neonatal hypoglycemia, macroglossia, visceromegaly, omphalocele, hemihypertrophy, and a propensity for the development of embryonal tumors, especially Wilms tumor (although many different types have been reported). c
c References , , , , , , , , .
Elliot and Maher suggested that the major criteria for diagnosis are macroglossia, overgrowth abnormalities, and anterior chest wall defect. Ear creases, flame-shaped facial nevi, kidney enlargement, hypoglycemia, and hemihypertrophy are considered minor criteria. Most patients have a birth weight greater than the 90th percentile. Most cases are sporadic, but autosomal dominant transmission is suspected. Deletions and translocations in chromosome 11, near the locus of insulin-like growth factor II, have been identified; this finding suggests a correlation between hypoglycemia and the growth stimulation resulting in hemihypertrophy and soft tissue overgrowth. Some 7% to 9% of patients with Beckwith-Wiedemann syndrome have tumors, but those with hemihypertrophy are at substantially greater risk (24%–27%) for the development of tumor. d
d References , , , , , , , .
Nonsyndromic hemihypertrophy is most commonly associated with Wilms tumor, but it has been linked to adrenal carcinoma and hepatoblastoma as well. As pointed out by Ballock and colleagues, most patients with Wilms tumor do not have hemihypertrophy, and no large prospective study of the incidence of tumor in nonsyndromic hemihypertrophy has been reported. Wilms and other tumors can be identified with abdominal ultrasonography. Unfortunately, reliable criteria for diagnosing nonsyndromic hemihypertrophy and for determining the incidence of tumor, the effectiveness of screening in altering the natural history, the frequency with which screening examinations should be performed, and the age at which screening can be stopped are unknown or unavailable. Thus no specific guidelines regarding the indications for or frequency of screening abdominal ultrasonography can be provided. At our institution, we perform abdominal ultrasonography in patients with the diagnosis of nonsyndromic hemihypertrophy or Beckwith–Wiedemann syndrome every 6 months until these patients are 8 years old.
Limb length inequality is a potential complication after long-bone fracture, particularly femoral shaft fracture. , , , The discrepancy may develop from malunion, growth stimulation, or subsequent disturbance of physeal growth. In a study of 50 children younger than 10 years of age who had femoral shaft fracture treated by spica immobilization within 72 hours of injury, Corry and Nicol found that 44 had overgrowth an average of 7 mm, 5 had retarded growth, and 1 showed no effect of treatment. Overgrowth was most likely in the 4- to 7-year-old age group. Hougaard, in a study of 67 patients with femoral shaft fracture, found that overgrowth averaged 10 mm, with a maximum of 2.6 cm; he could not correlate the extent of overgrowth with age, sex, or fracture pattern. Patients with shortening on follow-up tended to be older and to have fractures with angulation.
The possible relationship of leg length inequality with any number of lower extremity or spinal problems has provoked considerable debate in the medical arena and in other health care fields. Some studies have implicated a variable amount of leg length inequality in the development of scoliosis, low back pain, sciatica, excessive stress on hip or knee joints, and lower extremity dysfunction such as stress fracture, plantar fasciitis, or parapatellar knee pain.
Orthopaedists have traditionally been taught to consider leg length equalization by some means when, in the absence of other deformities, the leg length inequality exceeds or is expected to exceed 2 to 2.5 cm at skeletal maturity. e
e References , , , , , .
However, a firm rationale for this approach is lacking. A careful review of the literature reveals a lack of consensus regarding the amount of discrepancy that should serve as the threshold beyond which treatment is indicated.
Bhave and colleagues evaluated gait parameters in 18 patients before and after an average lengthening of 4.7 cm. These investigators found that significant differences in stance time between the short and long legs improved after lengthening and that the second peak of the vertical ground reaction force in the shorter limb improved significantly after lengthening. Eleven patients had complained of lumbosacral pain preoperatively, but none did after lengthening.
Brand and Yack evaluated the resultant hip forces and moments in seven normal control subjects walking with lifts of 2.3, 3.5, and 6.5 cm. The 2.3-cm lift produced no effect; the other lifts modestly increased mean peak intersegmental resultant hip forces but not moments in the shorter limb.
Goel and associates studied the gaits of 10 subjects without leg length inequality who were walking with a 1.25-cm lift under one foot and 10 asymptomatic patients with leg length inequality of 1 to 2 cm who were walking both with and without corrective lifts. In the group with equal leg length and in the group with the unequal leg length but walking without a lift, no side-to-side joint moment abnormalities were noted. In the group of patients with unequal leg length who were walking with corrective lifts, side-to-side joint moment differences were significantly increased. The authors concluded that “minor” leg length inequality does not produce predictable changes in joint kinetics that are likely to lead to joint abnormalities.
Kaufman and colleagues, in a gait analysis of 20 subjects with leg length inequality, noted that gait asymmetry beyond that seen in the normal population became evident when the discrepancy exceeded 2 cm (3.7%). This asymmetry was variable among subjects but was generally characterized by increased loading on the longer limb. Liu and associates, in a study of 30 patients with leg length inequality, found that discrepancies less than 2.3 cm resulted in “acceptable” gait asymmetry. In addition, these investigators noted that the amount of correction provided by a lift was unpredictable. Song and colleagues used gait analysis to evaluate 35 children with leg length inequality ranging from 0.6 to 11.1 cm (0.8%–15.8% shortening). Compensatory mechanisms included circumduction or persistent flexion of the longer limb, vaulting over the longer limb, and toe-walking on the shorter limb. Discrepancies of less than 3% were not associated with compensatory mechanisms. More mechanical work was performed by the longer leg, and there was a greater vertical displacement of the center of body mass when discrepancies exceeded 5.5%—a discrepancy that could not be compensated for by toe-walking.
The association between leg length inequality and low back pain in the adult population is not clear in the literature. An increased incidence of leg length inequality in patients with chronic low back pain has been noted by some authors , , , but not by others. f
f References , , , , , , , .
Amelioration of preexisting low back pain after leg length equalization by either surgical lengthening or surgical shortening has been reported by several authors. , , Similarly, the influence of leg length inequality on the morphology of the spine with or without associated low back pain is controversial; some authors have noted changes in facet joint orientation and other morphologic asymmetries, , , whereas other authors have not observed such changes. , , Leg length inequality has been implicated in the susceptibility of athletes and armed forces recruits to injury by some authors, , , , but not by others. , ,
It is important that an assessment of leg length inequality be incorporated into screening examinations performed by both orthopaedists and primary care physicians because, in the absence of pain or limb dysfunction, children can tolerate and mask even substantial discrepancies. When screening a child for limb length inequality or when assessing a complaint of such, the physician should determine how long the family has been aware of the apparent inequality and whether the child has any associated functional limitations in either limb, any family history of skeletal dysplasia, and any history of fracture, infection, or other significant injury to either extremity. Significant malformations such as congenital clubfoot deformity, skin discoloration, or soft tissue enlargement should be investigated.
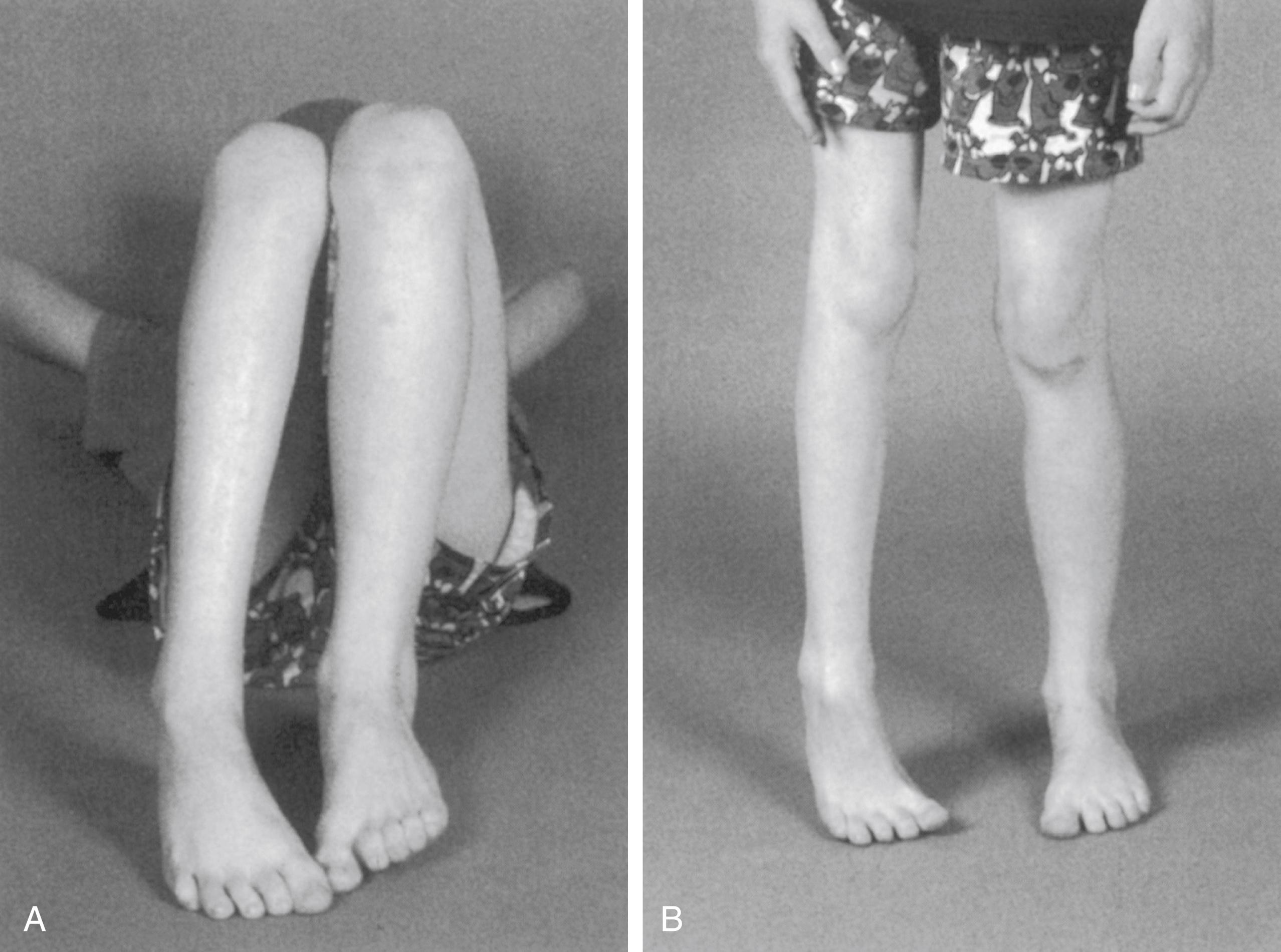
Leg length inequality determined by physical examination can be structural in response to a measurable difference in a lower extremity segment, functional (or postural) secondary to asymmetry in the positioning of one lower extremity relative to the other, or a combination of these. An accurate assessment of the nature of the leg length inequality must include both careful measurement of the length of the lower extremities and their segments and an evaluation of the range of motion and resting position of the lumbar spine, hips, knees, and ankles. An excellent illustration of the impact of functional limb length inequality that manifests as structural inequality is provided by the gait and clinical assessment of patients with hemiparesis. Relatively minor hip adduction or flexion contractures of the involved side produce the casual clinical impression of substantial structural leg length inequality, whereas the actual structural discrepancy of the femur or tibia is typically quite small ( Fig. 20.2 ). Ireland and Kessel estimated that a functional discrepancy of 3 cm was created with each 10-degree increment in hip adduction or abduction deformity, up to 40 degrees.
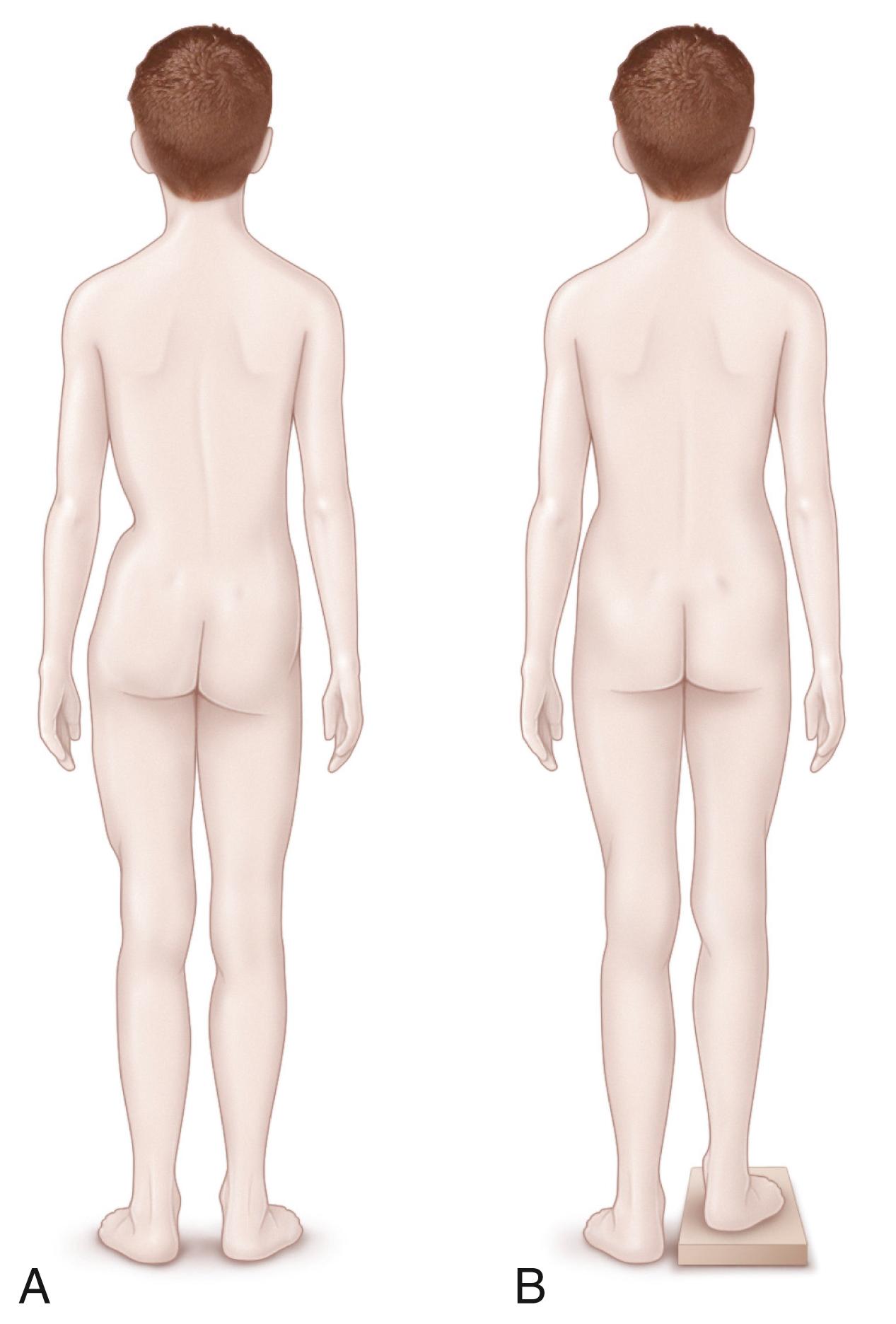
During a routine screening examination or the initial examination for a complaint of leg length inequality, the child should stand facing away from the examiner and should be undraped such that the examiner can see the legs and waist, including the posterior iliac spines. The examiner must be sure that the child is standing evenly, with the knees extended and the feet flat on the floor. In this position, the examiner can rest his or her hands on the iliac crests or look at the posterior iliac spines for evidence that one leg is longer than the other. If a discrepancy is evident, the extent of the discrepancy can be estimated by having the patient stand with graduated blocks under the shorter leg until the pelvis is level ( Fig. 20.3 ). Young, nonambulatory, or uncooperative children can be assessed while they are supine on an examining table; the examiner draws the child’s legs parallel in an extended position and notes the relative levels of the soles of the feet or the medial malleoli, and then the examiner flexes the hips 90 degrees and notes the relative knee height (the Galeazzi sign). It is important that the legs be held in symmetric positions at the hips, knees, and feet; otherwise, a functional discrepancy from an alteration in the position of the joints may be interpreted as a structural discrepancy.
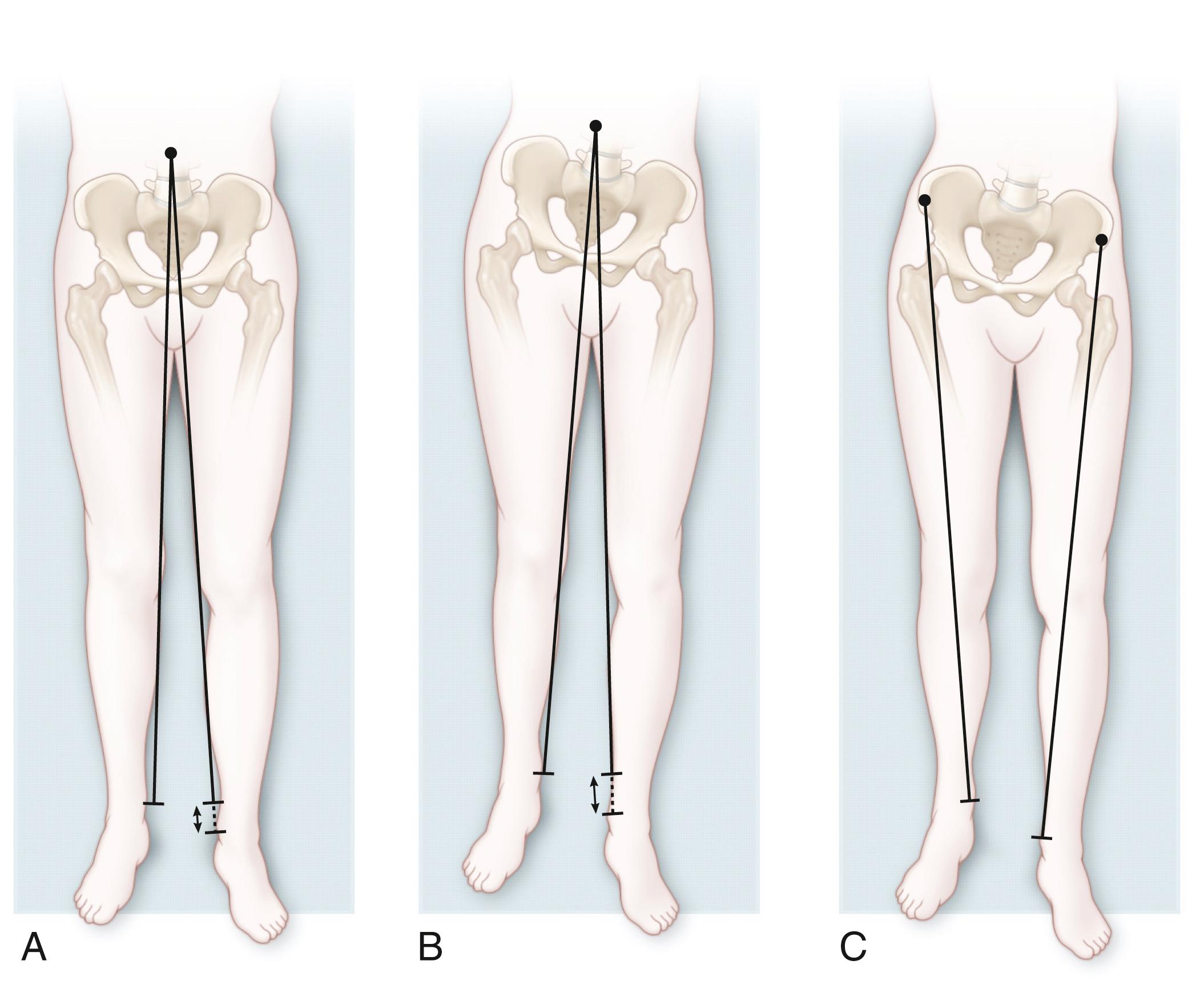
The limbs can be measured with a tape measure from the superior iliac spine to the medial joint line and the medial malleolus or from the umbilicus to the medial malleolus for functional discrepancies ( Fig. 20.4 ). However, measurement with a tape is susceptible to error because of variations in the location of these bony landmarks or difficulty identifying them or because of variations in the position of the joints (particularly the hip) during these measurements. g
g References , , , , , .
Smith described a clinical method for assessing leg length inequality called the “thigh-leg” technique. The patient is placed supine on an examining table with the hips and knees flexed 90 degrees. Discrepancies are measured between the table and the thigh, between the thighs at the knees, and between the soles of the feet with the knees even ( Fig. 20.5 ). Smith found this clinical method significantly superior to tape measurement and slightly more accurate than block measurement.
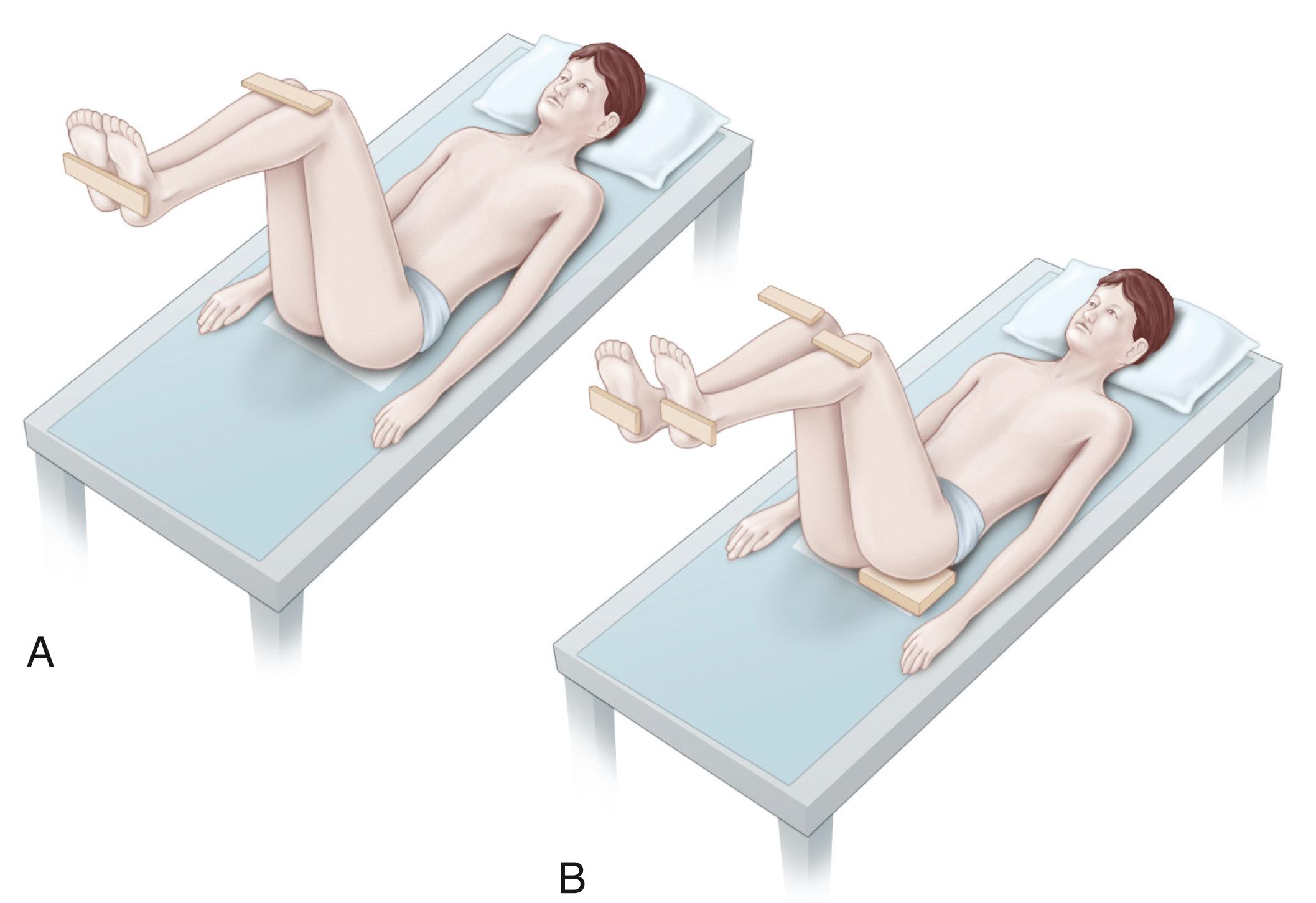
The examiner should carefully assess the arc of motion, resting position, and stability of the lower extremity joints. Simultaneously, the examiner looks for the following: angular deformity of the long bones; vascular, skin, or soft tissue anomaly in the limbs; spinal deformity; and vascular anomaly over the spine. In patients with suspected idiopathic hemihypertrophy or hemiatrophy, the physician should also look for asymmetry of upper extremity length, hand size, or facial features. Neurologic examination of the lower extremities that concentrates on motor strength, tone, and reflexes should be performed to complete the “static” screening assessment. Finally, the examiner watches the patient walk and run to gain insight into how much functional impairment is being produced by the leg length inequality, with or without associated deformity. During this portion of the examination, the examiner notes any compensatory mechanisms the patient is using, such as circumduction of the long leg, vaulting over the long leg, excessive flexion of the hip and knee of the long leg, or toe-walking on the short leg.
Radiographic documentation of leg length inequality can be accomplished with an anteroposterior (AP) radiograph of the pelvis with the patient standing with an appropriately sized block ( Fig. 20.6 ) under the shorter limb, scanograms, orthoroentgenograms, or computed tomography (CT) scanograms. h
h References , , , , , , , , , , , , , , , , , .
Ultrasonography has also been described for leg length inequality screening. ,

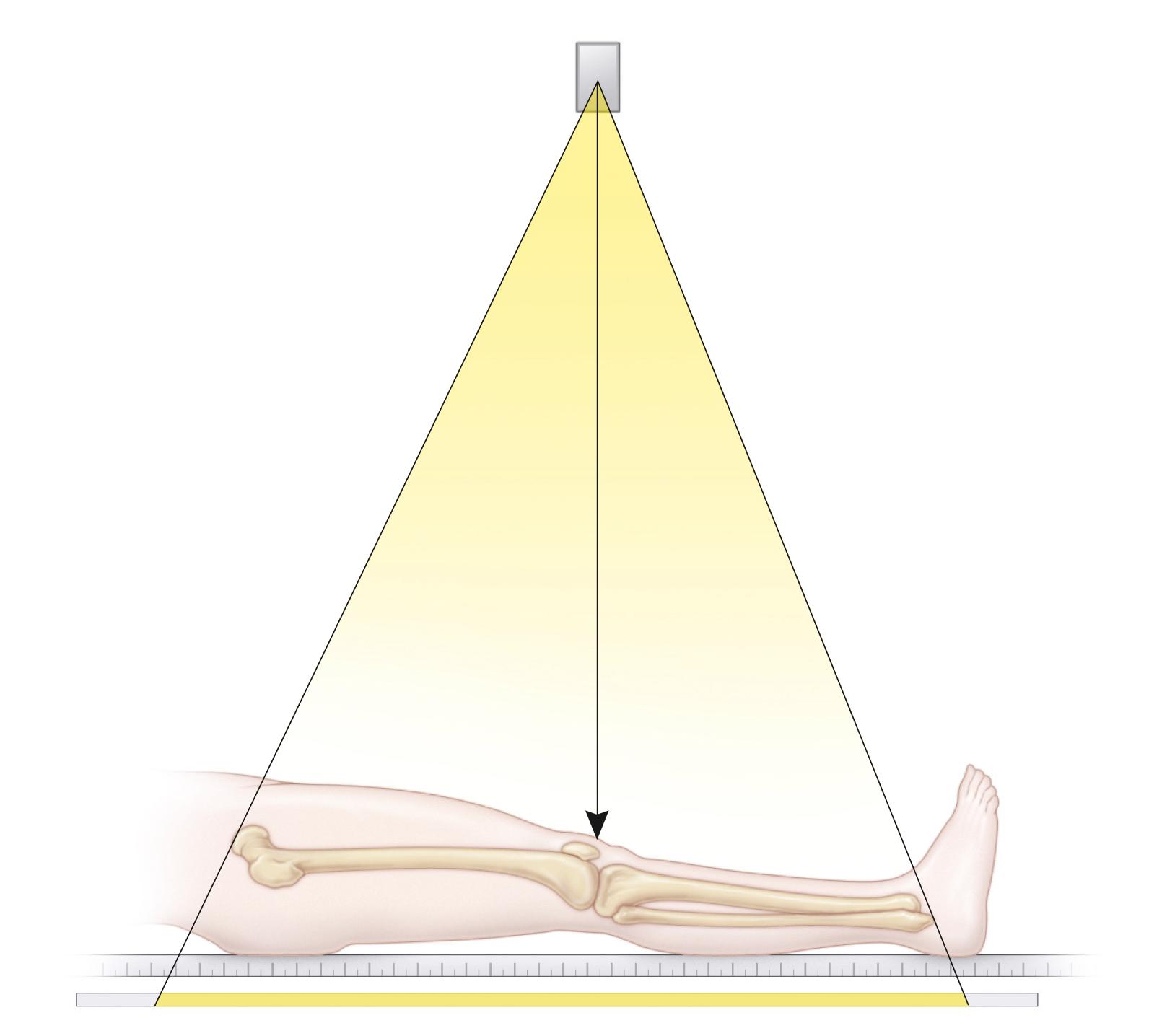
Teleoroentgenography is the simplest whole-leg radiographic technique for the assessment of leg length inequality. A radiograph of the entire lower extremity is obtained with the patient supine on the radiography table, with a long film and radiographic ruler beneath them. This technique is also the most susceptible to magnification error because a single exposure is made from a midpoint on the patient’s lower extremities ( Fig. 20.7 ). However, it is useful if the patient is unlikely or unwilling to hold still for multiple-exposure techniques.
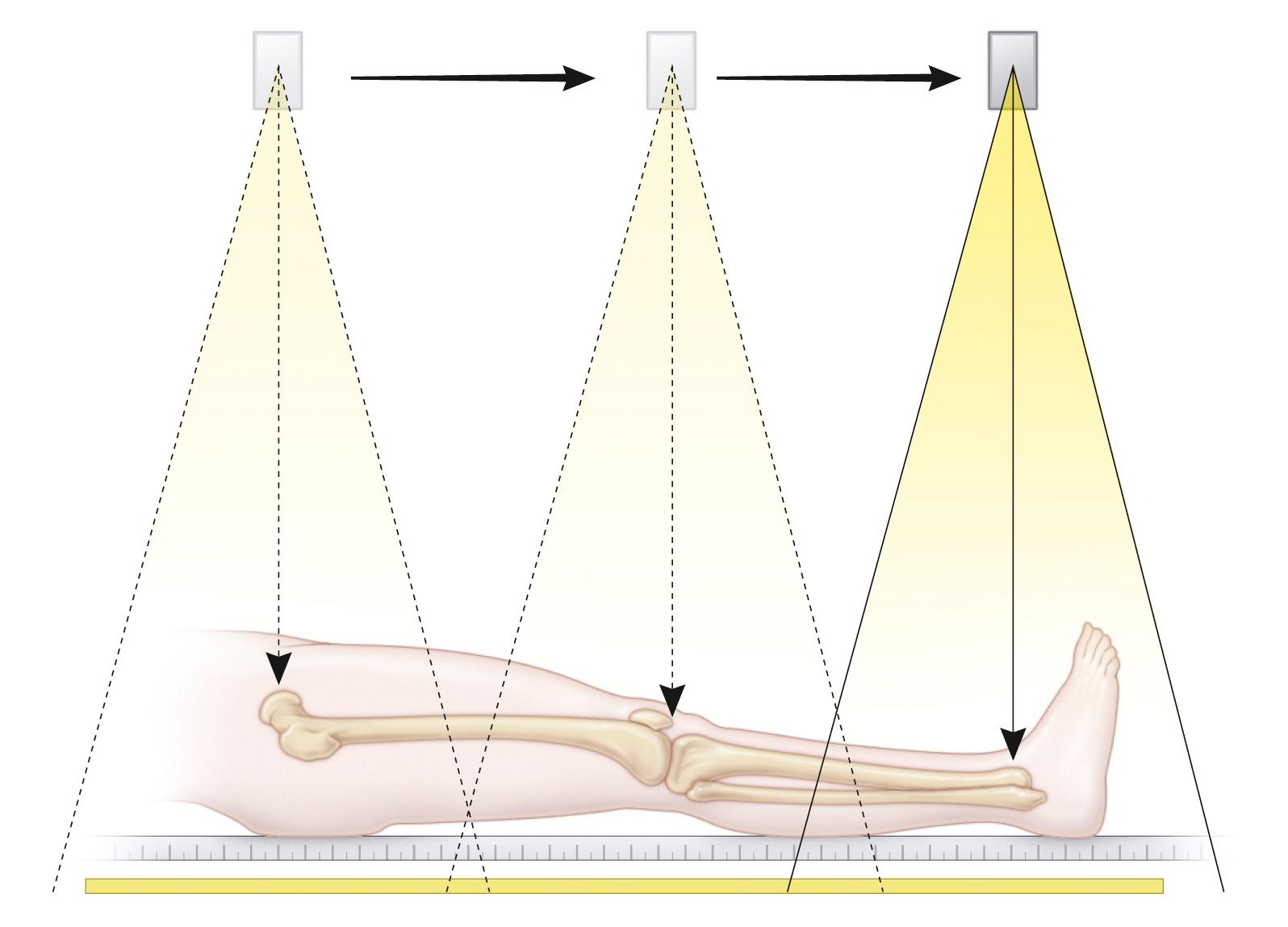
Orthoroentgenography is a radiographic technique described by Green and colleagues in 1946. The purpose is to minimize measurement error resulting from magnification by making three separate exposures of the lower extremities centered over the hips, knees, and ankles ( Fig. 20.8 ). One long film with a radiographic ruler is obtained, similar to in the teleoroentgenogram. In patients with significant leg length inequality, separate exposures for each leg may be made, with the x-ray beam centered over each joint. It is important that the patient not move between exposures (Green and colleagues ensured this immobility by strapping the patient to the table after positioning) and that the limbs be aligned neutrally. Saleh and Milne described the use of this technique in a weight-bearing position so that angular deformities, mechanical axis deviations, and limb length can be assessed simultaneously in that position. Weight bearing is not important to the accurate measurement of leg length inequality.
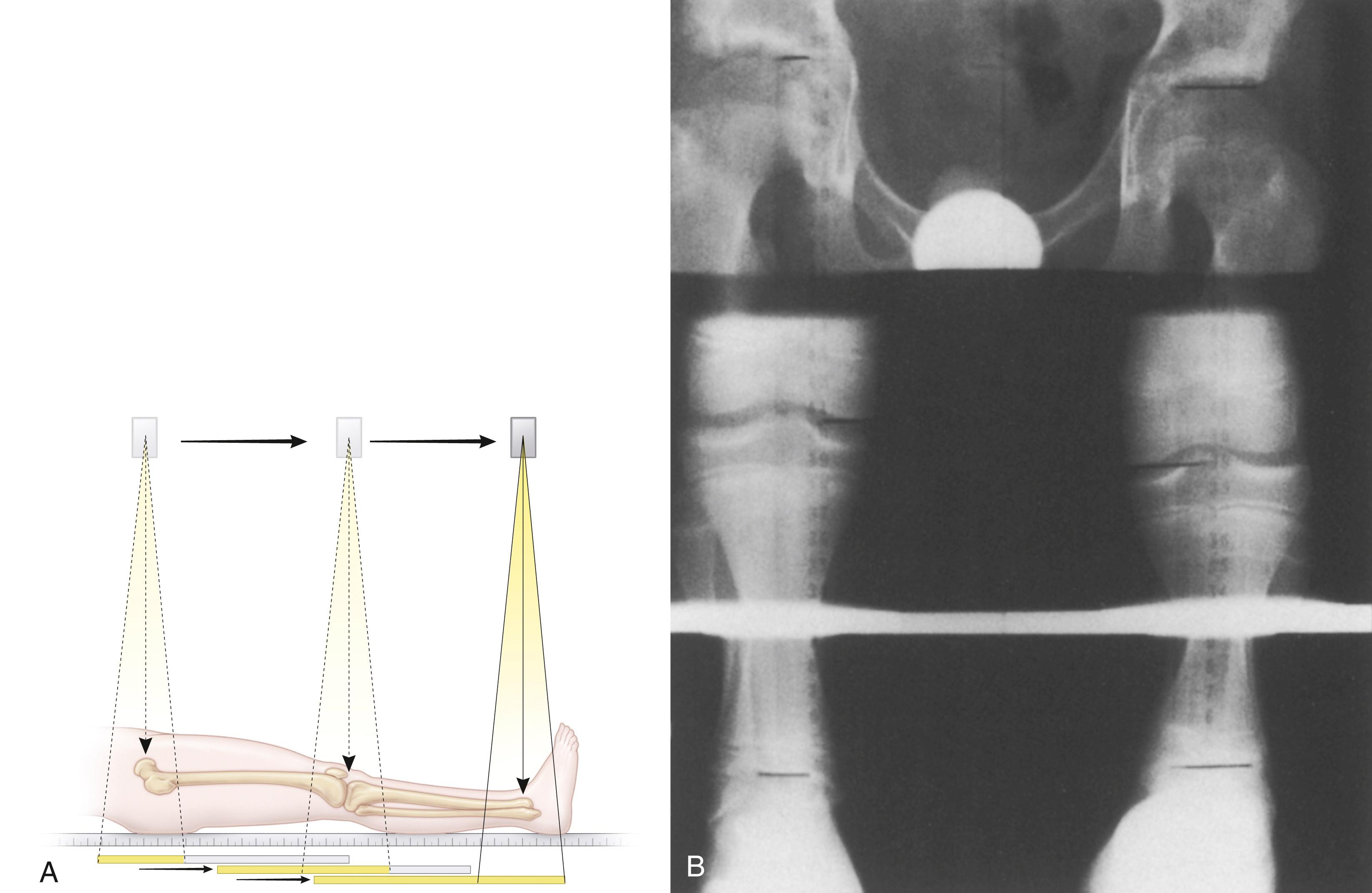
The term scanography arose from an early technique called slit scanography, but it has come to be used for a technique similar to orthoroentgenography. Scanography differs from orthoroentgenography in that, in addition to movement of the x-ray tube over the patient for three exposures, the film is moved under the patient ( Fig. 20.9 ). This approach reduces the size of the film required and makes storage and handling easier. As in orthoroentgenography, the patient must remain motionless during the exposures. The entire length of the bone is not available on film, thus negating this technique as a screening tool to assess the cause of leg length inequality. The EOS radiology technique offers accurate measurement of limb length discrepancy with minimal radiation.
An alternative to conventional radiography is low-dose computed radiography. The radiation dosage exposure with this method is significantly reduced (as little as 1% of the exposure with conventional radiography for orthoroentgenograms), and the accuracy is comparable to that of conventional radiography. ,
CT has become popular for the assessment of leg length inequality. i
i References , , , , , , .
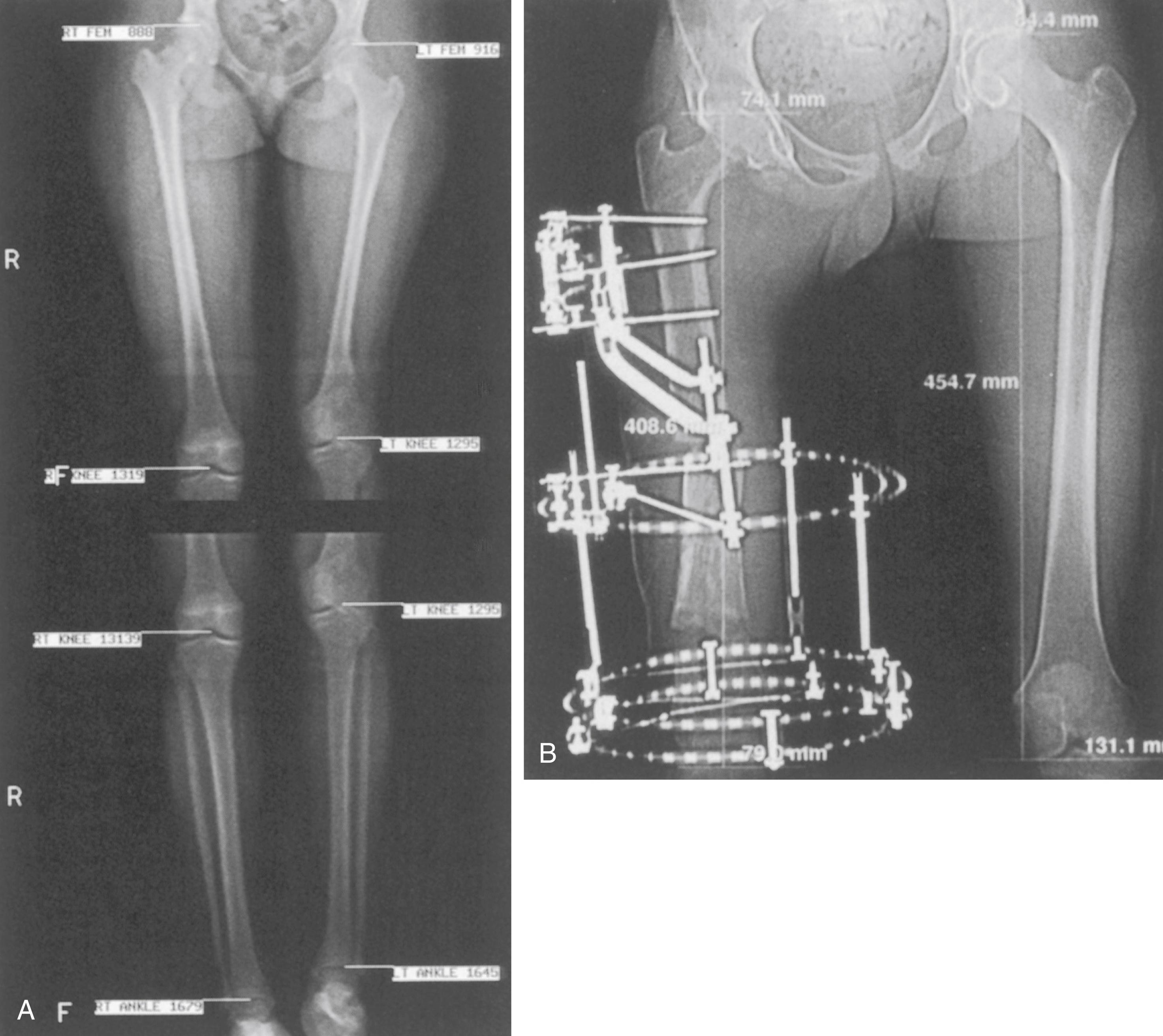
Advantages include lower radiation exposure even when the entire limb is exposed, greater accuracy, less susceptibility to error if the patient is poorly positioned, and the ability to accommodate positioning difficulties secondary to joint contractures or the presence of external fixators ( Fig. 20.10 ). This technique is specifically indicated when the patient has a knee flexion contracture or is in a circular external fixator because the accuracy is greater than that of conventional orthoroentgenography under these conditions. , , The radiology technicians responsible for obtaining CT scanograms must position the patient’s limbs symmetrically or should at least ascertain that a given positioning difficulty will not interfere with accurate measurement. For example, hip or knee flexion contractures are well accommodated by CT when measurements of segment length are taken from the lateral projection, but only if the limb is in a neutral position with respect to abduction or adduction at the hip or there is no asymmetric frontal plane angular deformity.
Ultrasonography has been used for the assessment of leg length inequality. , Junk and colleagues found that this technique was more accurate than clinical assessment alone, and Terjesen and associates found the accuracy to be within 2 mm of standard radiographic techniques. However, special jigs must be constructed, and the patient must not move during the examination. The main advantage of this technique is that exposure to ionizing radiation is not required. We have no experience with this technique of assessing leg length inequality.
An appreciation of normal skeletal growth of the lower extremities is an integral component of the evaluation and appropriate management of leg length inequality. Normal physeal growth, the contribution of each lower extremity physis to the overall length and shape of the leg, the concept and timing of skeletal maturation, and the impact of various disorders on normal growth are all components of that understanding.
All long bones are characterized as having five regions: the central tubular shaft (diaphysis), which flares into the funnel-shaped metaphyses at each end of the diaphysis, and the relatively bulbous, articular ends (epiphyses). Before skeletal maturity, the epiphysis and metaphysis are separated by the cartilaginous growth plate, or physis.
Traditionally, epiphyses have been characterized as one of two types: pressure or traction. Pressure epiphyses are articular, located at the end of a long bone, and contribute to the formation of a joint. The greatest portion of the longitudinal growth of a long bone takes place at the physes, which form part of the pressure epiphyses. Traction epiphyses are nonarticular; they serve as sites of origin or insertion for muscles, such as the greater and lesser trochanters, the tuberosities of the proximal humerus, the epicondyles of the distal humerus, and the tibial tubercle. The concept of the growth plate oversimplifies the anatomy of the physis and the epiphysis, and in many epiphyseal areas, it is a much more complex structure than a simple “plate.” For example, the upper end of the femur initially incorporates the greater trochanter, femoral neck, and femoral head. With growth and maturation, secondary ossification centers develop in the greater trochanter and head (capital epiphysis), with organization of the proximal growth plate into a continuous physis from the base of the greater trochanter, along the outer femoral neck, and extending into the base of the femoral head. Finally, the physeal portion of the upper end of the femur separates into the greater trochanteric physis (apophysis) and the capital physis (see Chapter 13 ). Other examples of complex physes include the proximal and distal humerus and the triradiate cartilage of the pelvis. Moreover, the epiphyses themselves grow circumferentially, not just at the plate.
The major long bones—femur, tibia, fibula, humerus, radius, and ulna—have a physis at each end. The short tubular bones—phalanges, metatarsals, and metacarpals—typically have one physis that is located proximally in the phalanges, first metacarpal, and first metatarsal and distally in the other metacarpal and metatarsal bones.
Long bones lengthen at the cartilaginous areas of their extremities. This was shown by Hales in 1731. He marked the shafts of the limb bones of newly hatched chicks with two holes. Two months later, the limb bones had increased considerably in length; however, the distance between the two marker holes had not increased. In 1736, Belchier discovered a new method of marking osseous tissue in pigs by feeding them madder root. Several years later, Duhamel’s studies of bone growth demonstrated that only the osseous tissue formed during the time the animal was fed madder turned red; the tissue formed before and after was of normal color.
In addition to confirming the findings of Hales that the longitudinal growth of long bones takes place at the extremities, Duhamel proposed that interstitial growth occurs to a varying extent in the diaphysis. He also demonstrated that transverse growth of the diaphysis occurs by appositional bone formation from the periosteum, not by interstitial growth in the bone tissue. The experiments of Hales and Duhamel were repeated by Hunter, who showed that appositional bone formation is accompanied by resorption of previously formed bony tissue. Flourens found that resorption of bony tissue is not confined to the endosteal aspect of the diaphysis but also occurs in most parts of bony tissue. Subsequently, it was noted that longitudinal growth could be influenced by mechanical factors, specifically, compression and traction or tension.
In 1862, both Hueter and Volkmann noted that compressive forces in bone resulted in a slowing of growth and that tension increased bone growth and the formation of osseous tissue (the Hueter-Volkmann principle). , Wolff disputed this, believing that both compression and tension resulted in bone growth stimulation. Haas in 1945 and Gelbke in 1951 demonstrated that wire loops placed around the distal femur in dogs impeded longitudinal bone growth. Haas also noted that pins placed across the physis could restrict longitudinal growth. Gelbke stated that the controversy regarding the influences of compression and tension on longitudinal growth arose from a failure to distinguish between growing and mature bone and that bone tissue formation and bone growth were considered identical processes. When he placed loose and tight wire loops around the distal femurs of growing dogs, Gelbke found that longitudinal growth continued for several months, until pressure developed across the physis; the physis then narrowed radiographically and histologically, and growth inhibition followed. Gelbke also noted that these changes were reversible if the wires were cut after physeal narrowing and growth inhibition had occurred. He also attempted to produce traction on an apophyseal physis with wire loops, with less success. He concluded that the effect of tension on the physis does not increase enchondral bone growth and appears to have the same effect as compression.
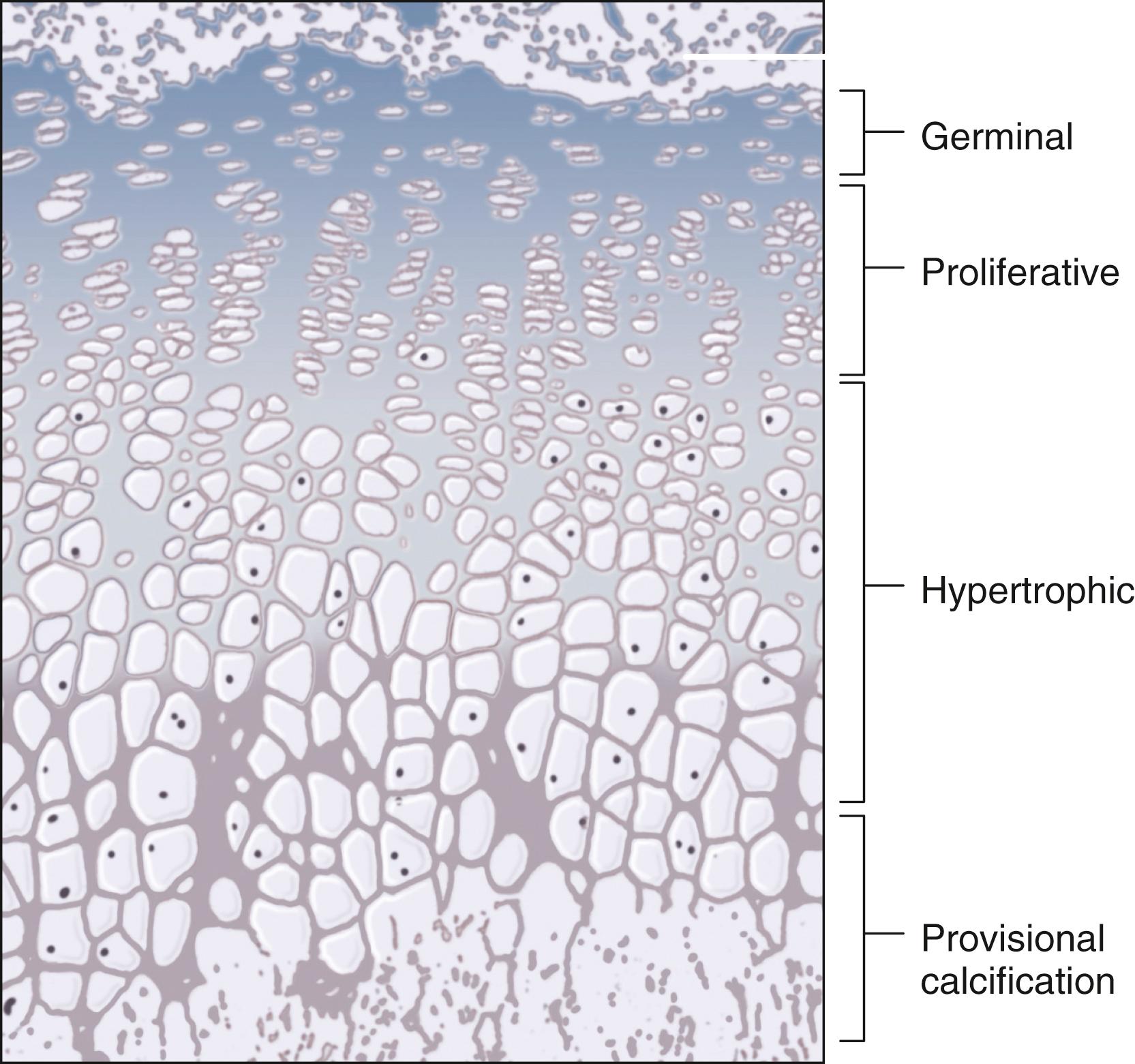
The physis is divided into horizontal zones termed germinal, proliferative, hypertrophic, and provisional calcification ( Fig. 20.11 ). The entire process of growth in this fashion—longitudinal growth by the cartilaginous “plate,” followed by ossification of the cartilaginous precursor—is known as enchondral ossification. Horizontal or peripheral growth of the physis occurs as well, in the specialized groove of Ranvier. The control of longitudinal growth and the mechanisms of cartilage cell hypertrophy, calcification, and ossification are still not thoroughly understood and are subject to many central and local hormonal and mechanical influences. The most widely recognized central hormonal regulator of physeal growth is growth hormone (GH). GH deficiency is associated with proportionate short stature, and excess GH secretion in the skeletally immature results in gigantism. GH action on physes is mediated by insulin-like growth factors produced in both the liver and physeal chondrocytes. Another important class of polypeptides (at least 10 classes have been identified) influencing normal physeal activity consists of the fibroblast growth factors, which have a mitogenic influence on physeal chondrocytes. A genetic defect in the fibroblast growth factor-3 receptor is responsible for achondroplasia.
Longitudinal growth of the epiphyses themselves is usually not taken into account when estimating the longitudinal growth of a particular long bone. Clinical and radiographic anthromorphometric measurements of the long bones during growth are usually made from the ends of the epiphysis; the contributions to longitudinal growth of the physes at both ends of the long bones of the upper and lower limb segments are known and are limited to the physes themselves. Thus, as Moseley has pointed out, growth data on the length of the leg and its femoral and tibial segments pertain to the entire length of the bone from epiphysis to epiphysis, but calculations regarding final length by virtue of growth from the physes ignore the increase in length provided by the epiphysis. , , , ,
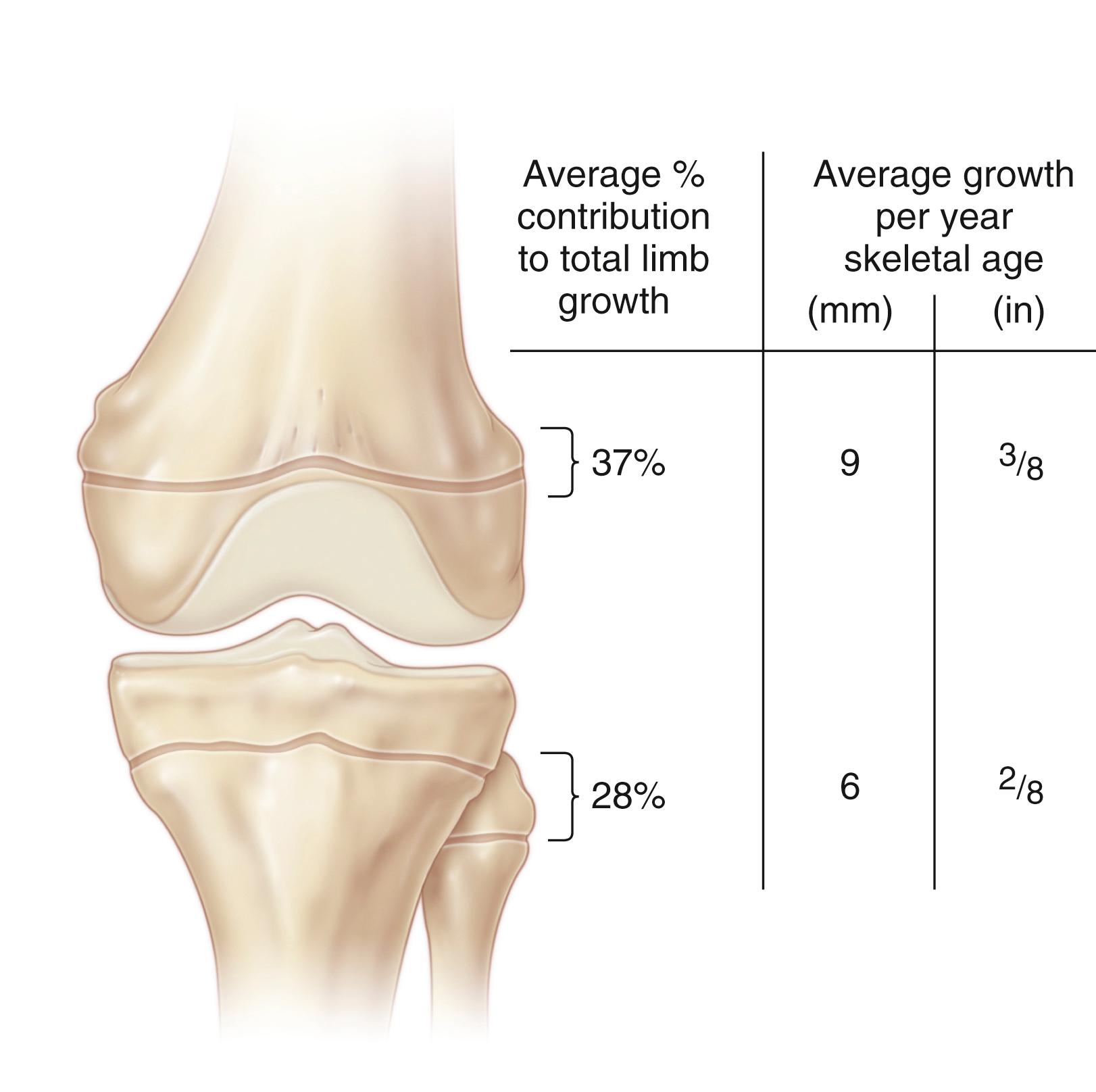
In long bones with physes at each end, the contribution of each physis to the longitudinal growth of the bone is typically asymmetric (see Fig. 1.9). Digby studied the contribution of longitudinal growth by assessing growth arrest lines in anatomic specimens. Anderson and colleagues estimated the contributions to longitudinal growth of the distal femur and proximal tibia by assessing sharply delineated growth arrest lines on consecutive radiographs in a semilongitudinal study of 206 boys and girls. These investigators found that 71% of femoral growth occurred distally, and 57% of tibial growth occurred proximally.
The timing of the appearance of the secondary centers of ossification, which make the physis radiographically identifiable, also varies by location and, to some extent, by individual. Finally, the timing of closure with cessation of longitudinal growth in individual physes also varies by location and individual (see Figs. 1.5 and 1.7 for these approximations).
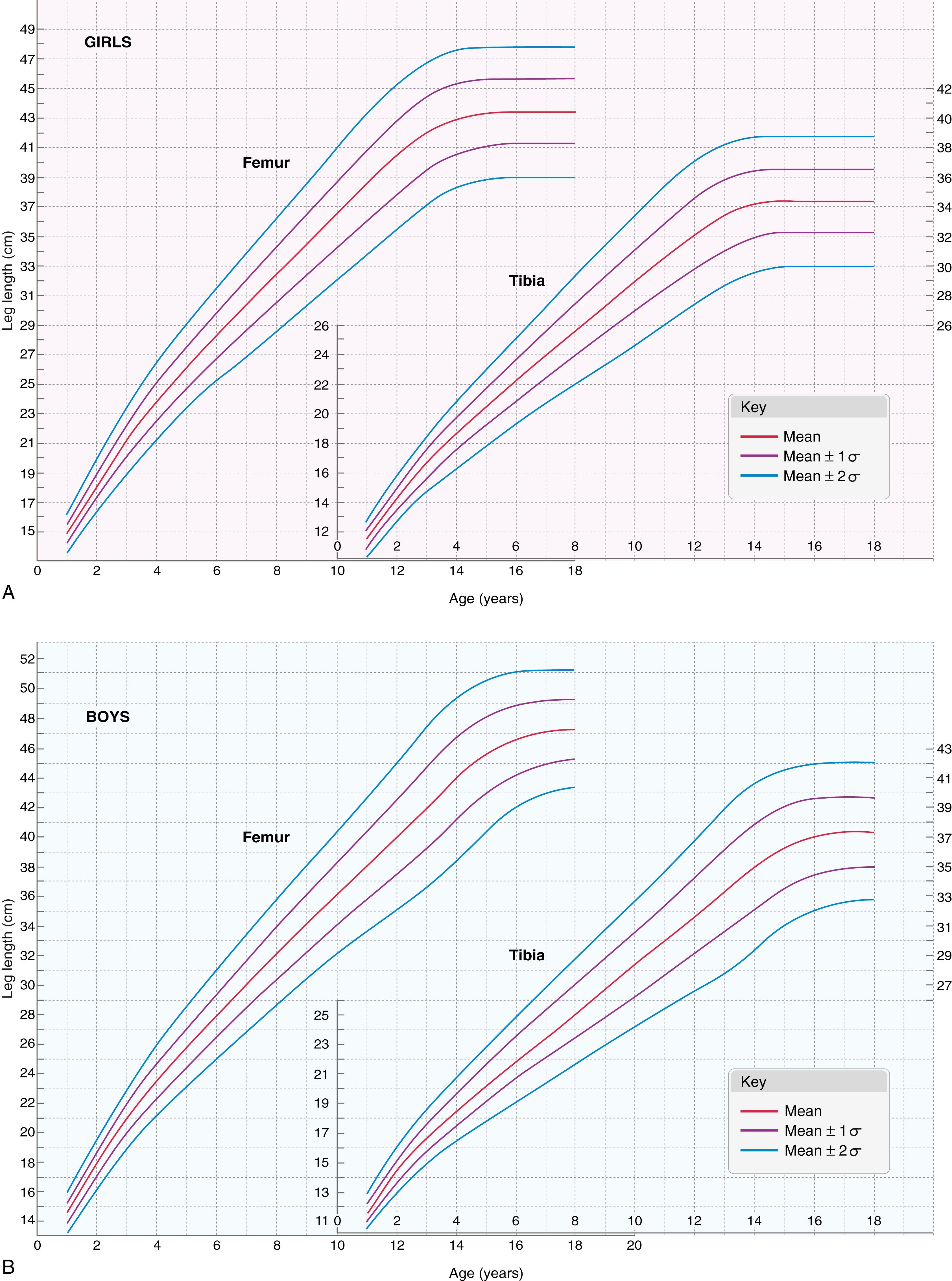
Anderson, Green, and Messner published two articles that provide important information on the longitudinal growth of the femur and tibia and an estimation of growth remaining that can be used to time epiphysiodesis or stapling. , The first article, published in 1963, examined longitudinal growth data obtained in 100 children (50 boys and 50 girls) who were assessed at least once a year in the 8 years before their growth terminated. Fifty-one of the children were normal (25 girls and 26 boys), and 49 had poliomyelitis affecting only one lower extremity; the data from the normal legs of these 49 children were incorporated into the data from the normal children. Orthoroentgenograms (measuring the length of the femur and tibia, including each epiphysis), hand and wrist films for skeletal age (using Greulich and Pyle’s atlas ), total body size, and other variables were measured at each visit. Visits were scheduled close to the subjects’ birthdays, and measurements (including skeletal age) were recorded against chronologic age ( Table 20.1 ).
| Age (yr) | Stature (cm) | Femur (cm) | Tibia (cm) | Skeletal Age (yr) | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | σ | Mean | σ | Mean | σ | Mean | σ | |
| 50 Girls | ||||||||
| 8 | 128.1 | 4.78 | 33.1 | 1.63 | 26.3 | 1.39 | 7.6 | 1.02 |
| 9 | 133.8 | 4.78 | 35.0 | 1.71 | 28.0 | 1.50 | 8.7 | 1.02 |
| 10 | 139.9 | 5.24 | 37.0 | 1.82 | 29.8 | 1.67 | 9.9 | 1.03 |
| 11 | 146.6 | 5.93 | 39.2 | 2.00 | 31.6 | 1.84 | 11.1 | 1.07 |
| 12 | 153.2 | 6.36 | 41.1 | 2.12 | 33.2 | 1.95 | 12.5 | 1.12 |
| 13 | 158.3 | 6.14 | 42.4 | 2.12 | 34.2 | 1.94 | 13.8 | 1.06 |
| 14 | 160.8 | 6.16 | 43.1 | 2.15 | 34.5 | 1.97 | 14.8 | 1.05 |
| 15 | 162.3 | 6.02 | 43.2 | 2.18 | 34.6 | 1.98 | 15.8 | 1.00 |
| 16 | 162.9 | 6.10 | 43.3 | 2.20 | 34.6 | 2.00 | 16.4 | 0.92 |
| 17 | (163.8) | (6.37) | (43.3) | (2.21) | (34.7) | (2.00) | (17.1) | (0.85) |
| 18 | (164.9) | (6.10) | (43.3) | (2.21) | (34.7) | (2.00) | (17.8) | (0.46) |
| 50 Boys | ||||||||
| 8 | 127.6 | 5.94 | (32.8) | (1.53) | (25.9) | (1.55) | (7.8) | (1.00) |
| 9 | 133.3 | 6.15 | (34.6) | (1.78) | (27.1) | (1.86) | (8.8) | (1.04) |
| 10 | 138.5 | 6.58 | 36.4 | 1.87 | 28.6 | 1.89 | 9.9 | 0.96 |
| 11 | 143.5 | 6.94 | 38.2 | 2.07 | 30.1 | 2.07 | 11.0 | 0.88 |
| 12 | 149.4 | 7.72 | 40.2 | 2.23 | 31.8 | 2.27 | 12.1 | 0.76 |
| 13 | 156.3 | 9.13 | 42.3 | 2.52 | 33.6 | 2.49 | 13.1 | 0.80 |
| 14 | 163.7 | 9.54 | 44.3 | 2.58 | 35.3 | 2.54 | 14.1 | 0.93 |
| 15 | 169.8 | 8.68 | 45.8 | 2.38 | 36.4 | 2.34 | 15.1 | 1.14 |
| 16 | 173.2 | 7.74 | 46.6 | 2.27 | 36.9 | 2.21 | 16.3 | 1.20 |
| 17 | 175.0 | 7.41 | 46.9 | 2.30 | 37.1 | 2.21 | 17.3 | 1.10 |
| 18 | 175.9 | 7.37 | 47.0 | 2.35 | 37.1 | 2.22 | (18.0) | (0.89) |
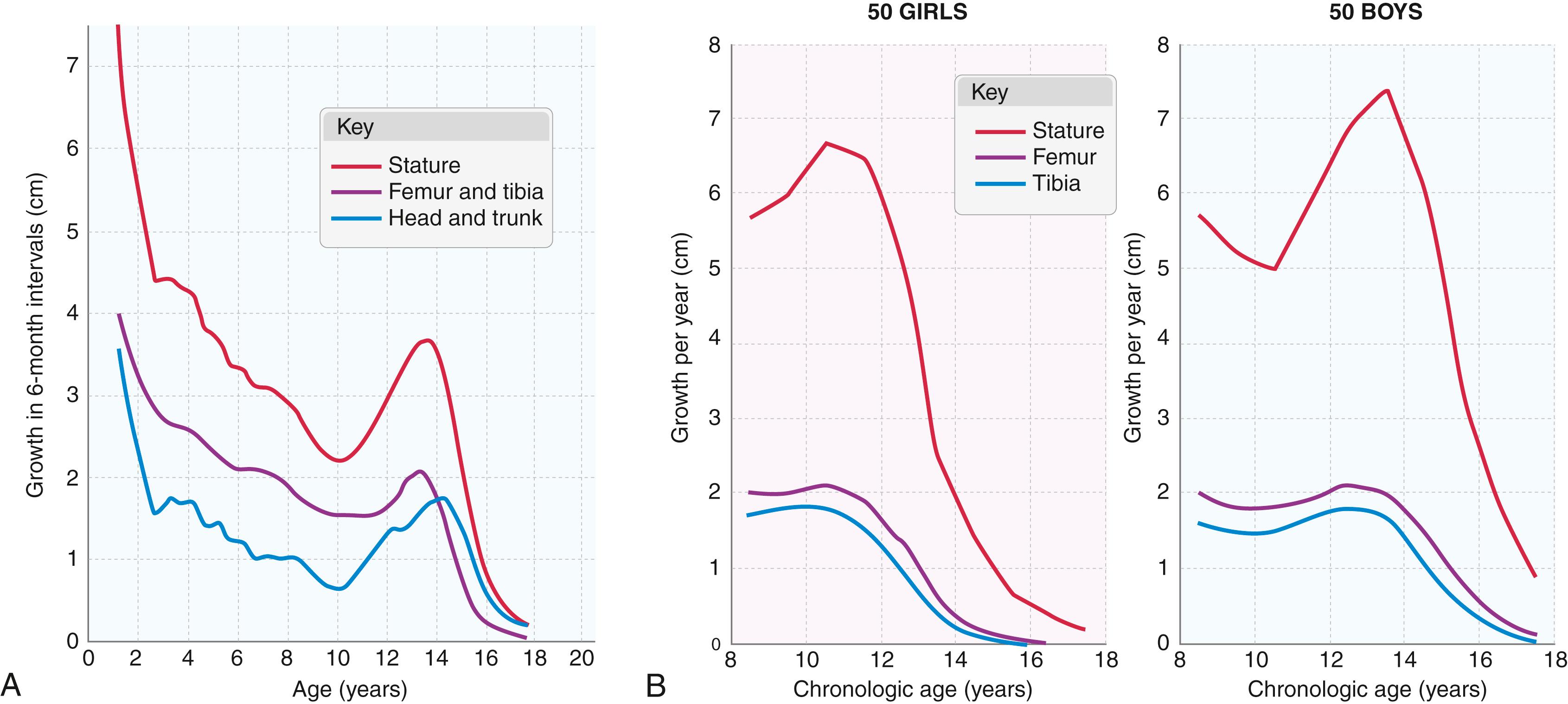
A number of interesting findings emerged from this study. The annual rate of overall growth (stature) rapidly decreased from birth to age 6 years and was stable from ages 6 through 9 years (average stature increment, 5.7 ± 0.93 cm). Femoral length increased at an average annual rate of 2.0 ± 0.27 cm, and tibial length increased at an average annual rate of 1.6 ± 0.23 cm. A pubertal growth spurt typically occurred sometime after age 9 years (and usually reached a maximum between 10 and 12 years of age in girls and between 12 and 14 years of age in boys). This growth spurt was followed by a final 4-year period of rapid decline in the rate of growth until cessation of growth ( Fig. 20.12 ). When average figures for stature and femoral or tibial length changes per year of chronologic growth were computed, the amplitude of the peak was blunted because the age at which the growth spurt occurred varied from one child to the next. In general, growth continued for 2 years after the adolescent growth spurt, irrespective of the age at which it occurred. As a consequence, although tables and graphs based on chronologic age are useful in younger children, because of this variation in the onset of the pubertal growth spurt these tables and graphs are not as valuable in children with 5 to 6 years of growth remaining.
Anderson and colleagues used skeletal age, as published by Greulich and Pyle, but noted that assessments from the elbow, hip, knee, and foot can also be used, as well as physical maturation parameters (such as Tanner’s stages of development; see Chapter 1 ). These authors found that when skeletal age was used as the basis for interval changes, the mean values for growth remaining were essentially the same as when chronologic age was used, but the recorded variation around the mean was appreciably less when skeletal age was used. Thus, more precise estimates of future growth in an individual child could be made by using skeletal rather than chronologic age, particularly in children whose level of maturation was consistently advanced or retarded 2 years or more compared with their chronologic age.
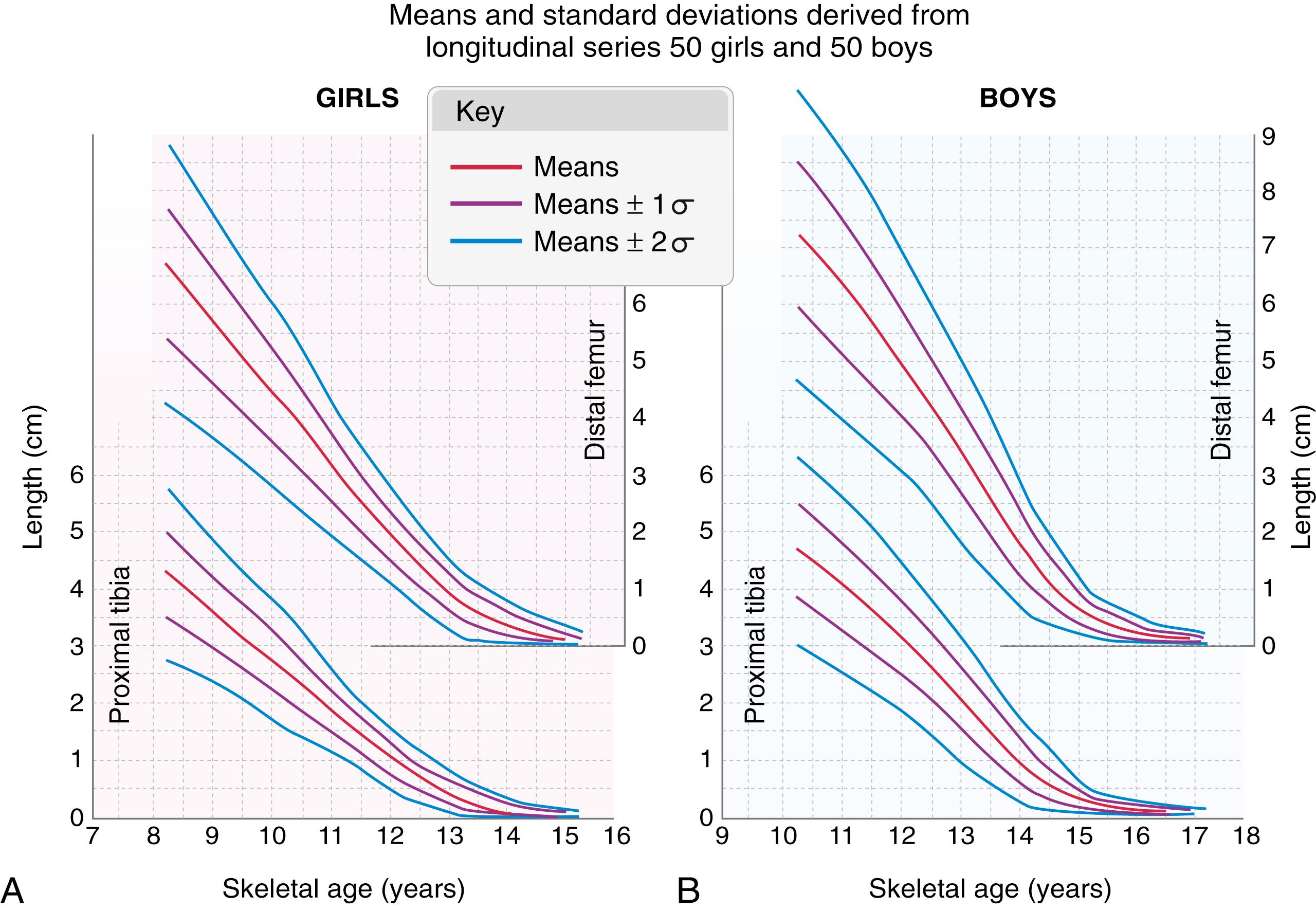
The method that Anderson and associates used to develop their growth-remaining charts was to interpolate the length of each of the 100 femora and tibiae at specific, equally spaced skeletal ages (10 years 3 months, 11 years 3 months, and so on). The increments of growth between these consecutive skeletal ages were derived. The growth of the entire femur and tibia was then related to the growth at the specific physes by using figures for the proportional contribution of growth obtained from the semilongitudinal study of sharply delineated growth arrest lines on consecutive radiographs (71% of femoral growth occurred distally, and 57% of tibial growth occurred proximally). These results were then used to compile the growth-remaining charts for boys and girls in the distal femur and proximal tibia ( Fig. 20.13 ). An example of the variations encountered was provided by Anderson and colleagues themselves, who noted that the 50th percentile growth remaining at the distal femur for a girl of skeletal age 10 years 3 months was 4.1 cm, whereas the extremes of growth that occurred at that age were actually from 2.2 to 7.2 cm; 80% of these girls were noted to grow between 3.3 and 5.0 cm.
Anderson and associates described how the growth-remaining charts were to be used in their 1963 article. Green and Anderson had presented less complete versions in 1947 and 1957. , The first consideration is the growth of the side not operated on. These investigators noted that the rate of growth inhibition in poliomyelitis is not constant over the entire period of growth and recommended determining the rate of growth in the 2 to 3 years before treatment by epiphysiodesis. In addition, if the physis of the affected leg is not growing at all, no correction should be expected, only prevention of further leg length inequality. The second consideration is the child’s relative maturity, the importance of which cannot be overemphasized. These investigators concluded that forming a total picture of each child is important, and they did not attempt to reduce the prediction of results to a precise, mathematical formula.
The second article by Anderson and colleagues, published in 1964, provided data on the length of the femur and tibia from a completely longitudinal study of 67 boys and 67 girls derived from radiographs taken on their birthdays from 1 to 18 years of age. The radiographs were teleoroentgenograms in younger children and orthoroentgenograms in older children. The authors used “appropriate” conversion factors on these 6-foot films to arrive at true femoral and tibial lengths. Recorded femoral length was “from the proximal articulating surface of the capital epiphysis to the most distal point on the lateral condyle,” and recorded tibial length was “from the mid-point of a line drawn across the proximal condyles to the mid-point of the distal articulating surface.” The data ( Tables 20.2 and 20.3 ) were used to generate length of femur and tibia graphs for boys and girls based on their chronologic ages ( Fig. 20.14 ). The difficulty of reconciling maturation and relative height can be seen in the authors’ example ( Fig. 20.15 ): longitudinal follow-up of a boy with hemihypertrophy showed a “dip” from 1 standard deviation above the norm to the norm during a period of presumed “delayed” maturation. Thus, assessment only during adolescence would give a false picture of the percentile length of the individual’s femur and tibia and lead to an underestimation of the amount of growth remaining during that time.
| Femur (cm) | |||
|---|---|---|---|
| No. | Age (yr) | Mean | σ |
| 21 | 1 | 14.48 | 0.628 |
| 57 | 2 | 18.15 | 0.874 |
| 65 | 3 | 21.09 | 1.031 |
| 66 | 4 | 23.65 | 1.197 |
| 66 | 5 | 25.92 | 1.342 |
| 67 | 6 | 28.09 | 1.506 |
| 67 | 7 | 30.25 | 1.682 |
| 67 | 8 | 32.28 | 1.807 |
| 67 | 9 | 34.36 | 1.933 |
| 67 | 10 | 36.29 | 2.057 |
| 67 | 11 | 38.16 | 2.237 |
| 67 | 12 | 40.12 | 2.447 |
| 67 | 13 | 42.17 | 2.765 |
| 67 | 14 | 44.18 | 2.809 |
| 67 | 15 | 45.69 | 2.512 |
| 67 | 16 | 46.66 | 2.224 |
| 67 | 17 | 47.07 | 2.051 |
| 67 | 18 | 47.23 | 1.958 |
| Tibia (cm) | |||
|---|---|---|---|
| No. | Age (yr) | Mean | σ |
| 61 | 1 | 11.60 | 0.620 |
| 67 | 2 | 14.54 | 0.809 |
| 67 | 3 | 16.79 | 0.935 |
| 67 | 4 | 18.67 | 1.091 |
| 67 | 5 | 20.46 | 1.247 |
| 67 | 6 | 22.12 | 1.418 |
| 67 | 7 | 23.76 | 1.632 |
| 67 | 8 | 25.38 | 1.778 |
| 67 | 9 | 26.99 | 1.961 |
| 67 | 10 | 28.53 | 2.113 |
| 67 | 11 | 30.10 | 2.301 |
| 67 | 12 | 31.75 | 2.536 |
| 67 | 13 | 33.49 | 2.833 |
| 67 | 14 | 35.18 | 2.865 |
| 67 | 15 | 36.38 | 2.616 |
| 67 | 16 | 37.04 | 2.412 |
| 67 | 17 | 37.22 | 2.316 |
| 67 | 18 | 37.29 | 2.254 |
| Femur (cm) | |||
|---|---|---|---|
| No. | Age (yr) | Mean | σ |
| 30 | 1 | 14.81 | 0.673 |
| 52 | 2 | 18.23 | 0.888 |
| 63 | 3 | 21.29 | 1.100 |
| 66 | 4 | 23.92 | 1.339 |
| 66 | 5 | 26.32 | 1.437 |
| 66 | 6 | 28.52 | 1.616 |
| 67 | 7 | 30.60 | 1.827 |
| 67 | 8 | 32.72 | 1.936 |
| 67 | 9 | 34.71 | 2.117 |
| 67 | 10 | 36.72 | 2.300 |
| 67 | 11 | 38.81 | 2.468 |
| 67 | 12 | 40.74 | 2.507 |
| 67 | 13 | 42.31 | 2.428 |
| 67 | 14 | 43.14 | 2.269 |
| 67 | 15 | 43.47 | 2.197 |
| 67 | 16 | 43.58 | 2.193 |
| 67 | 17 | 43.60 | 2.192 |
| 67 | 18 | 43.63 | 2.195 |
| Tibia (cm) | |||
|---|---|---|---|
| No. | Age (yr) | Mean | σ |
| 61 | 1 | 11.57 | 0.646 |
| 67 | 2 | 14.51 | 0.739 |
| 67 | 3 | 16.81 | 0.893 |
| 67 | 4 | 18.86 | 1.144 |
| 67 | 5 | 20.77 | 1.300 |
| 67 | 6 | 22.53 | 1.458 |
| 67 | 7 | 24.22 | 1.640 |
| 67 | 8 | 25.89 | 1.786 |
| 67 | 9 | 27.56 | 1.993 |
| 67 | 10 | 29.28 | 2.193 |
| 67 | 11 | 31.00 | 2.384 |
| 67 | 12 | 32.61 | 2.424 |
| 67 | 13 | 33.83 | 2.374 |
| 67 | 14 | 34.43 | 2.228 |
| 67 | 15 | 34.59 | 2.173 |
| 67 | 16 | 34.63 | 2.151 |
| 67 | 17 | 34.65 | 2.158 |
| 67 | 18 | 34.65 | 2.161 |
Menelaus reported on his experience with the White method (reported by White and Stubbins in 1944) in 1966 and reaffirmed this experience in 1981. , White had originally suggested that the distal femur grew ⅜ inch and the proximal tibia grew ¼ inch per year, with growth stopping at age 17 in boys and at age 16 in girls. Menelaus modified that assumption of growth cessation to age 16 for boys and age 14 for girls ( Fig. 20.16 ). He reported the results at skeletal maturity in 44 children who had undergone 53 epiphysiodeses using the Phemister technique and immobilization in plaster for 6 weeks. At skeletal maturity, 52% of the patients had leg length inequality within ¼ inch of the calculated discrepancy and 41% within ¾ inch of the calculated discrepancy; 7% had a residual discrepancy of more than ¾ inch. Menelaus stated that 89.6% of Green and Anderson’s patients were within ½ inch of the calculated discrepancy, compared with 80% of Menelaus’ patients.
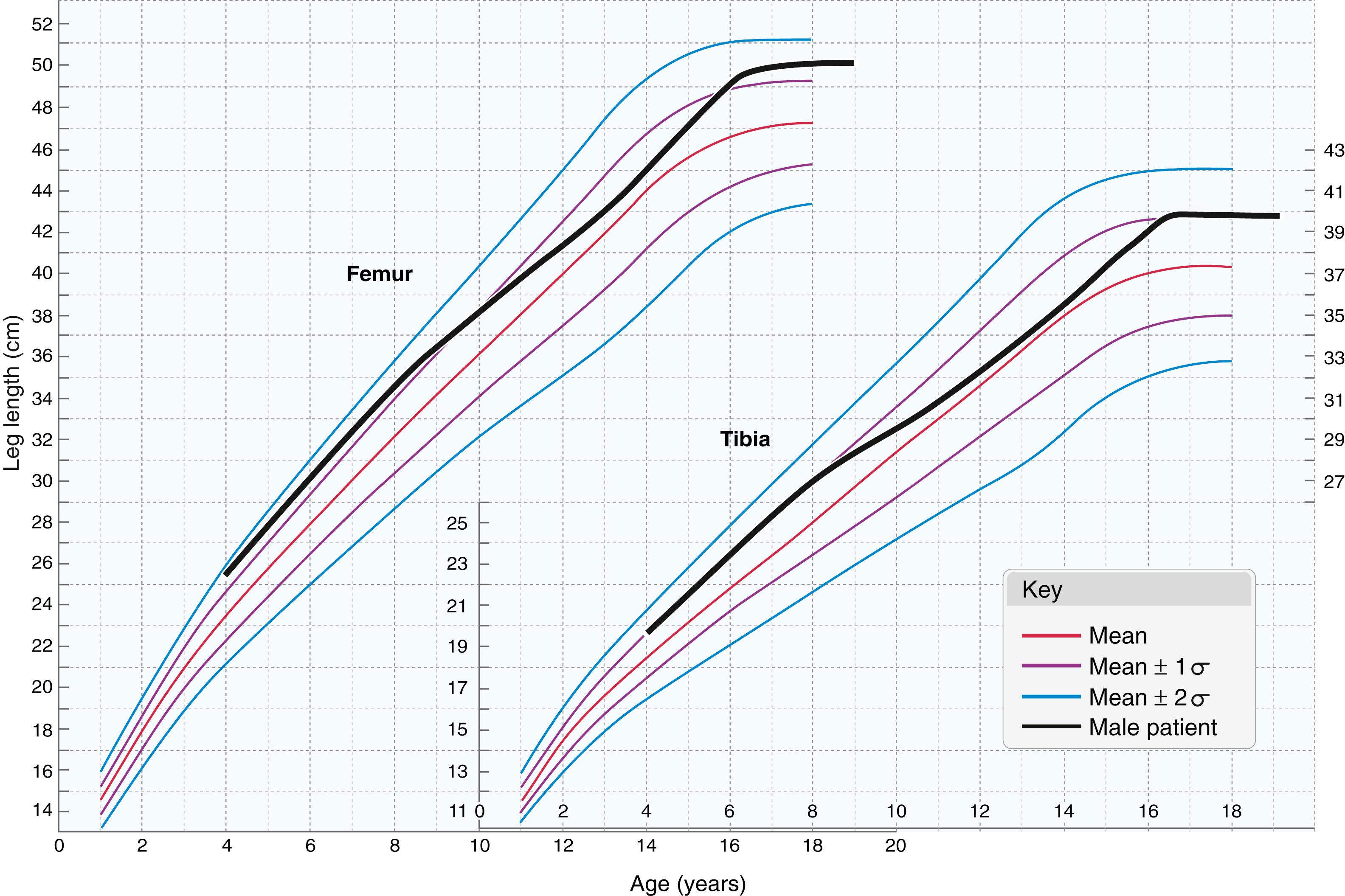
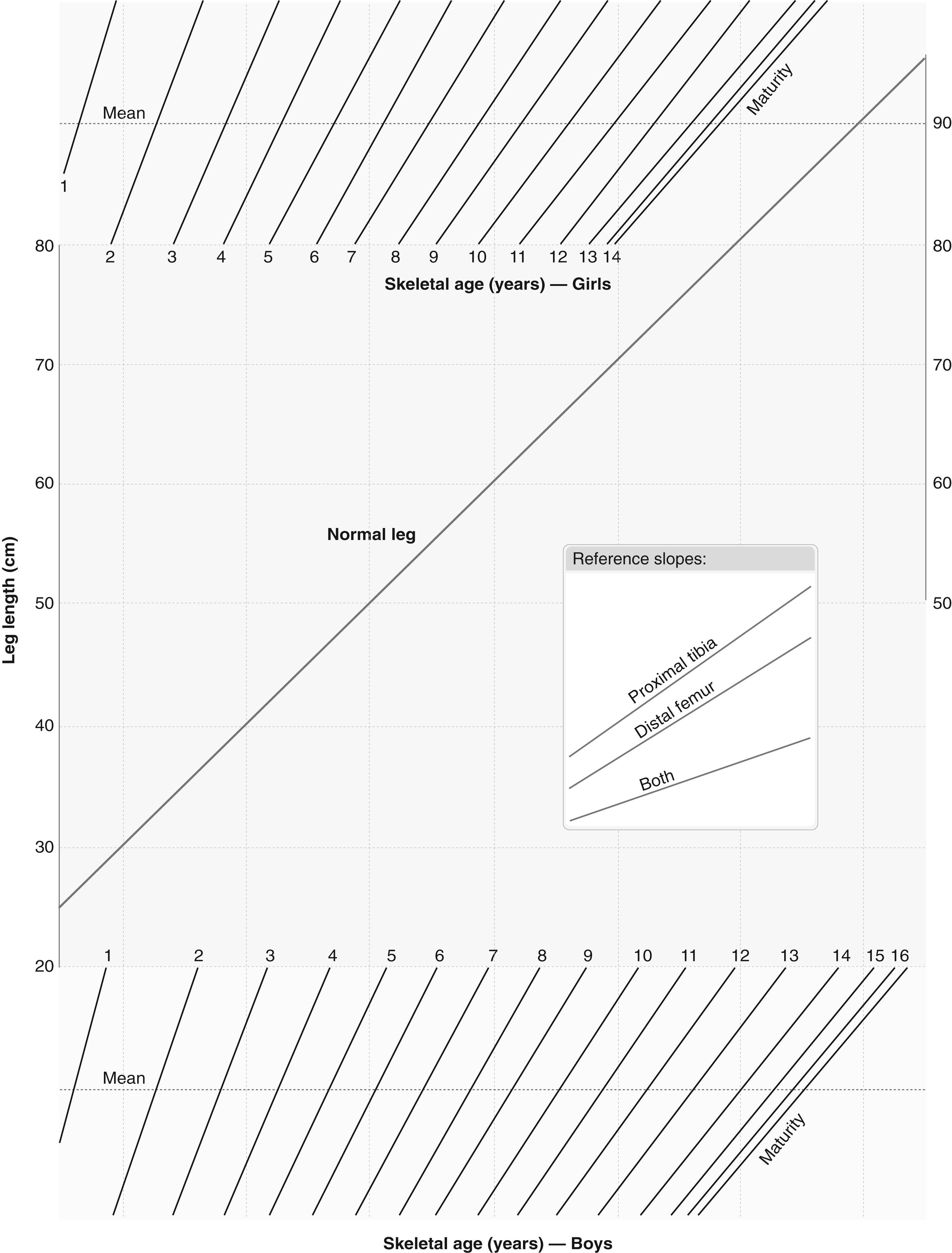
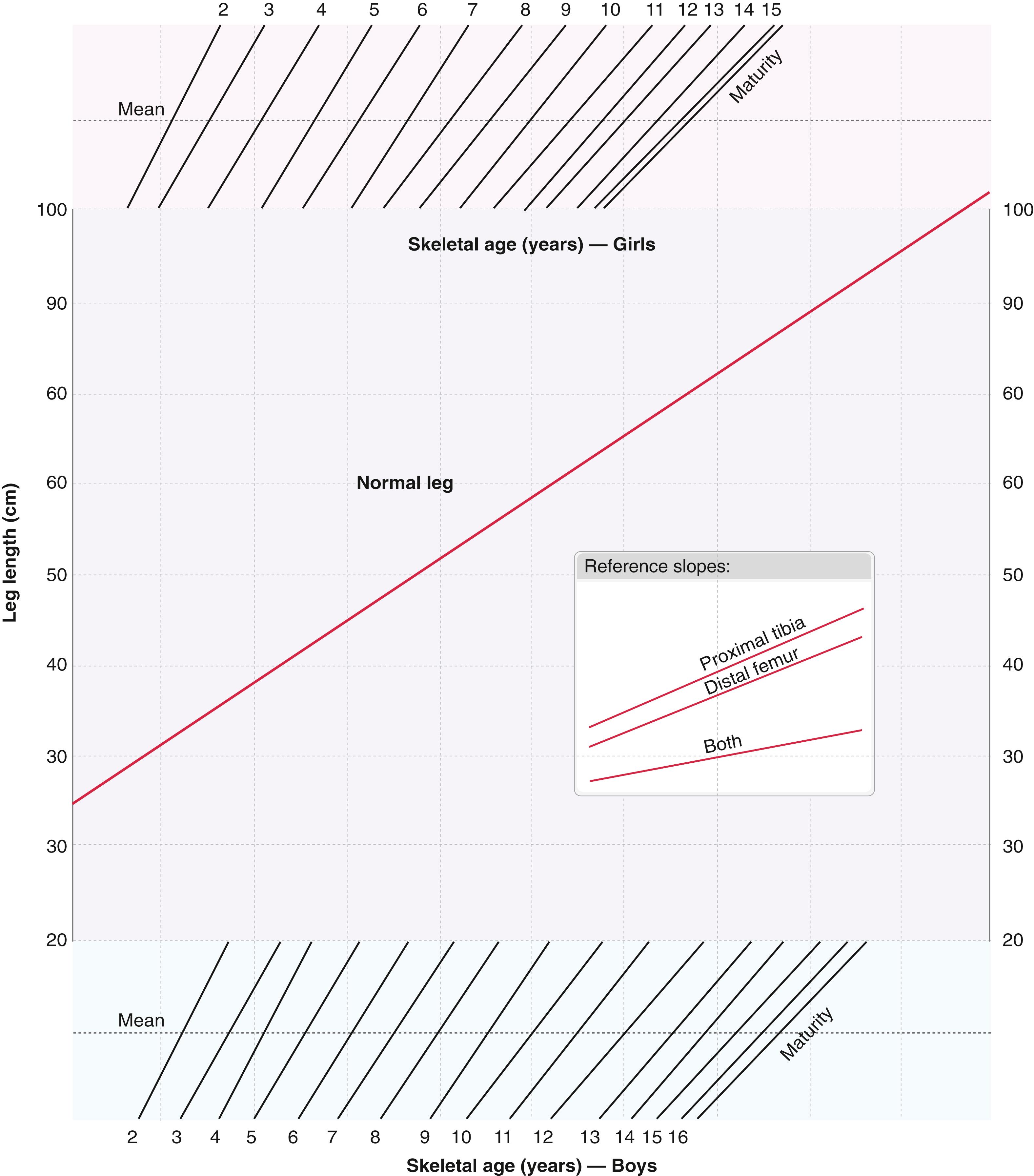
Moseley in 1977 described a straight-line graph method for calculating the ultimate discrepancy in a skeletally immature child and determining the timing of long-leg epiphysiodesis to correct leg length inequality. His method is discussed further in other publications. The graph was constructed based on a mathematical reanalysis of the chronologic growth data on the length of the femur and tibia in normal boys and girls that were published by Anderson and colleagues in 1964. The purpose of Moseley’s graph was to simplify and improve the accuracy of calculations intended to estimate the ultimate discrepancy in growing children by incorporating into the calculations skeletal maturation based on hand-wrist bone films, growth inhibition, and relative size. In his words, “the growth of the legs can be represented by straight lines by a suitable manipulation of the scale of the abscissa.” As a consequence, with the nomogram of skeletal age to correct for percentile growth (i.e., relative size and skeletal maturation), the growth of the short leg is represented as a straight line, and the leg length inequality is represented as the vertical distance between the lines; the line indicating the growth of the shorter leg has a less steep slope compared with that of the longer leg, and the growth inhibition effected by epiphysiodesis can be indicated by altering growth inhibition (slope of growth of the longer leg) by the expected amount, based on the type of epiphysiodesis performed . The reference line in Moseley’s straight-line graph refers to the growth of the normal leg rather than the long leg (see Fig. 20.18 ). This is important because, in cases of overgrowth (e.g., hemihypertrophy), the abnormal leg should be plotted above the normal, shorter leg; this has a slight impact on the subsequent depiction of the limbs, the projected final discrepancy at maturity, and the timing of epiphysiodesis. (See Plate 20.1 on page 861 for a detailed discussion of the application of the straight-line graph method of Moseley.) In a review of 23 skeletally mature patients who had undergone epiphysiodeses for leg length inequality, Moseley found that his straight-line graph method yielded a mean error of 0.6 cm in predicting ultimate leg length inequality, compared with a mean error of 0.9 cm when the Anderson-Green-Messner growth-remaining method was used.
FLOAT NOT FOUND
Some assumptions are incorporated into the construction and use of Moseley’s straight-line graph. Skeletal age–determined lengths of the femur and tibia do not exist for skeletal ages younger than 8 years in the data of Anderson and associates. , Moseley assumed that individual patients maintained the same percentile skeletal age but acknowledged that this is not necessarily the case. In fact, Anderson and colleagues pointed out the tendency for longer femora to grow less and shorter femora to grow more with subsequent maturation (which is one reason that the accuracy of the Menelaus modification of the White-Stubbins method is comparable to that of the Moseley method). Finally, the straight-line determination of growth of the shorter (abnormal) leg presumes that growth inhibition is linear; however, as both Moseley and Shapiro pointed out, this is not necessarily true. Despite these problems, the accuracy of this method in practice is generally good, and we routinely use this method at our institution to determine leg length inequality at skeletal maturity and the appropriate timing of epiphysiodesis of the long leg.
Paley and co-workers described the multiplier method to calculate leg length at skeletal maturity. , , These authors identified an arithmetic factor (multiplier) by dividing femoral and tibial lengths at skeletal maturity by the femoral and tibial lengths at different ages during growth for each percentile group, by using a variety of available leg length databases. The length of each leg and the difference in leg length at maturity (assuming constant growth inhibition) can be calculated by multiplying these measurements by the appropriate multiplier for the subject’s age and gender ( Table 20.4 ). One analysis found that the multiplier method was not accurate compared to methods based on skeletal age when used for timing arrest in patients with vascular malformations.
| Age (yr + mo) | Multiplier for Boys | Multiplier for Girls |
|---|---|---|
| Birth | 5.080 | 4.630 |
| 0 + 3 | 4.550 | 4.155 |
| 0 + 6 | 4.050 | 3.725 |
| 0 + 9 | 3.600 | 3.300 |
| 1 + 0 | 3.240 | 2.970 |
| 1 + 3 | 2.975 | 2.750 |
| 1 + 6 | 2.825 | 2.600 |
| 1 + 9 | 2.700 | 2.490 |
| 2 + 0 | 2.590 | 2.390 |
| 2 + 3 | 2.480 | 2.295 |
| 2 + 6 | 2.385 | 2.200 |
| 2 + 9 | 2.300 | 2.125 |
| 3 + 0 | 2.230 | 2.050 |
| 3 + 6 | 2.110 | 1.925 |
| 4 + 0 | 2.000 | 1.830 |
| 4 + 6 | 1.890 | 1.740 |
| 5 + 0 | 1.820 | 1.660 |
| 5 + 6 | 1.740 | 1.580 |
| 6 + 0 | 1.670 | 1.510 |
| 6 + 6 | 1.620 | 1.460 |
| 7 + 0 | 1.570 | 1.430 |
| 7 + 6 | 1.520 | 1.370 |
| 8 + 0 | 1.470 | 1.330 |
| 8 + 6 | 1.420 | 1.290 |
| 9 + 0 | 1.380 | 1.260 |
| 9 + 6 | 1.340 | 1.220 |
| 10 + 0 | 1.310 | 1.190 |
| 10 + 6 | 1.280 | 1.160 |
| 11 + 0 | 1.240 | 1.130 |
| 11 + 6 | 1.220 | 1.100 |
| 12 + 0 | 1.180 | 1.070 |
| 12 + 6 | 1.160 | 1.050 |
| 13 + 0 | 1.130 | 1.030 |
| 13 + 6 | 1.110 | 1.010 |
| 14 + 0 | 1.080 | 1.000 |
| 14 + 6 | 1.060 | |
| 15 + 0 | 1.040 | |
| 15 + 6 | 1.020 | |
| 16 + 0 | 1.010 | |
| 16 + 6 | 1.010 | |
| 17 + 0 | 1.000 |
The application of published longitudinal growth data and the methods of calculating growth remaining to determine the appropriate timing of epiphysiodesis for leg length inequality have several areas of potential inaccuracy. Identifying the cause of leg length inequality in children is important for determining the ultimate discrepancy at skeletal maturity. For example, total physeal destruction from infection, fracture, irradiation, or surgical ablation results in fairly predictable growth retardation from loss of growth of the affected physis for the duration of remaining skeletal growth. Congenital limb deficiencies characteristically cause consistent growth inhibition of the affected leg, so that the percentage of shortening remains fairly constant during skeletal growth even as the absolute amount of discrepancy increases. However, Shapiro pointed out that not all growth inhibition in growing children is linear (i.e., results in a constant percentage of growth inhibition or acceleration in the affected limb), as implied by the standard graphic methods of calculating ultimate leg length inequality. Eastwood and Cole noted a linear increase in discrepancy in only 8 of 20 patients treated by epiphysiodesis.
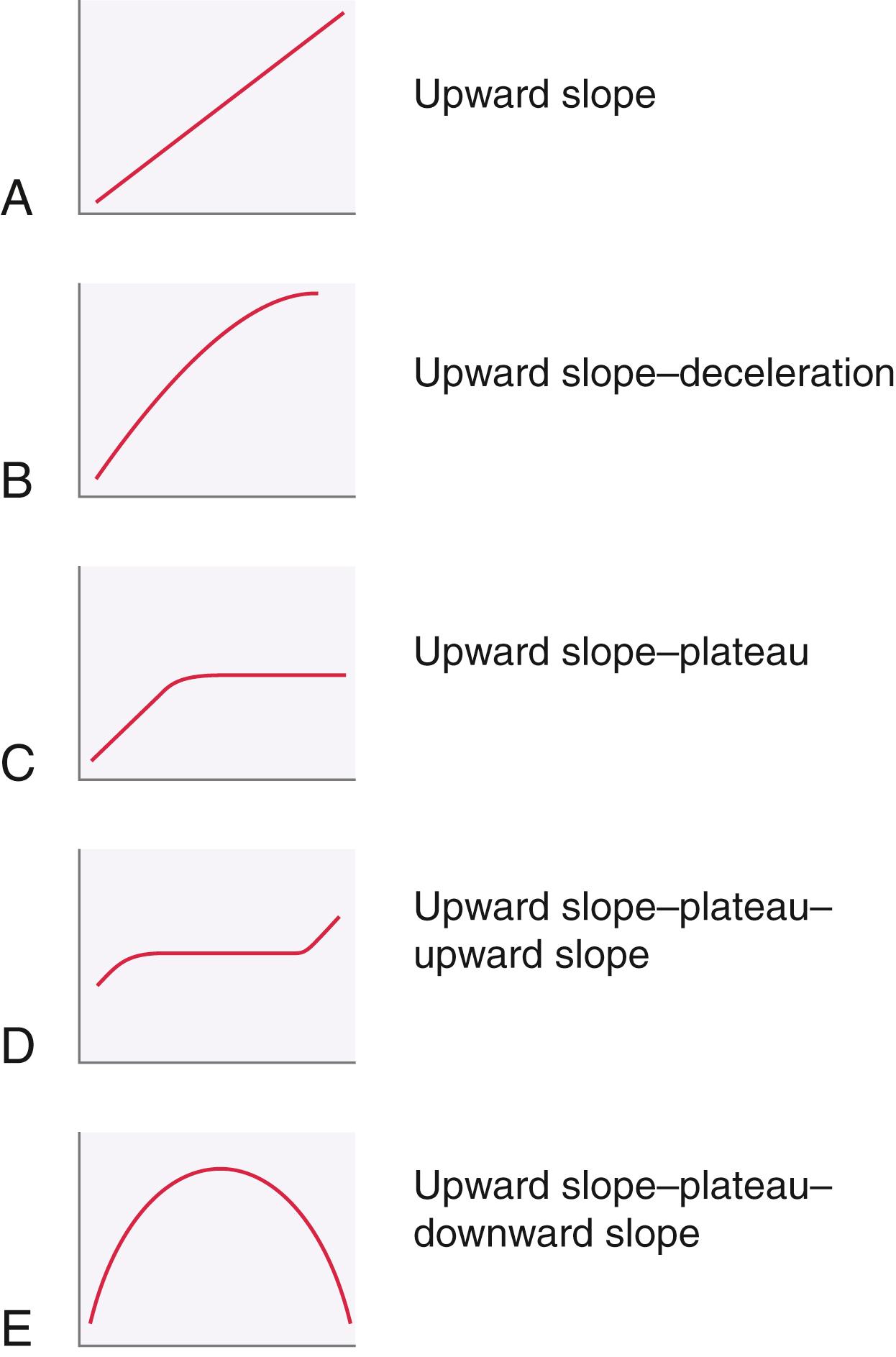
Shapiro described five basic patterns of leg length inequality development based on an assessment of discrepancy development in 803 patients ( Fig. 20.17 ). Type 1 is an upward slope pattern, implying a stable percentage of growth inhibition compared with the normal leg. Type 2 is characterized by an upward slope–deceleration pattern. Type 3 is characterized by an upward (or downward) slope–plateau pattern and is most typical of post–femoral shaft fracture overgrowth. In Shapiro’s series, growth in 85% of patients with overgrowth had plateaued by 3.5 years after fracture. Type 4 is an upward slope–plateau–upward slope pattern, seen only in abnormalities involving the proximal femur, such as septic arthritis, Legg-Perthes disease, and avascular necrosis (AVN) associated with the treatment of developmental dysplasia of the hip. Type 5 is characterized by an upward slope–plateau–downward slope pattern, meaning that an initially increasing discrepancy actually decreases with subsequent growth.
In Shapiro’s series, the type 1 growth pattern was typical of patients with proximal femoral focal deficiency, Ollier disease (enchondromatosis), congenital femoral deficiency with more than 6 cm of shortening, physeal obliteration from any cause, and poliomyelitis. Some patients with congenital femoral deficiency with less than 6 cm of shortening or with poliomyelitis tended to exhibit a type 2 pattern. Patients with idiopathic hemihypertrophy or hemiatrophy demonstrated type 1, 2, or 3 patterns. Only 31% of patients with overgrowth associated with vascular anomalies had type 1 growth, and the remainder had a type 2 or 3 pattern. Patients with neurofibromatosis most commonly had a type 1 pattern, but types 2, 3, and 5 were also seen. Similarly, patients with juvenile arthritis exhibited types 1, 2, 3, and 5 patterns. Patients with Legg–Perthes disease exhibited all five patterns.
Prediction of leg length inequality based on serial scanograms, hand and wrist radiographs for skeletal age, and straight-line graph analysis ( Figs. 20.18 and 20.19 ) has other potential pitfalls as well. j
j References , , , , , , , , , .
Kasser and Jenkins, in a study of normal leg growth in normal children between 5 and 10 years of age, found that, except in girls with advanced bone age, the use of Greulich and Pyle’s atlas in preference to chronologic age did not improve the accuracy of predicting leg length at skeletal maturity. There was a mean error of 2.4 cm by the Anderson-Green-Messner method and of 2.6 cm by the Moseley straight-line graph method when the prediction was based on skeletal age. Blair and colleagues found that only 22 of 67 patients treated by epiphysiodesis had a final discrepancy of less than 1 cm. Ten of the 45 failures resulted from inadequate epiphysiodesis, and 35 were caused by incorrect use of the growth prediction charts of Anderson and associates. Little and colleagues also found that use of Greulich and Pyle’s atlas and either the Anderson-Green-Messner charts or Moseley’s straight-line graph did not improve the accuracy of prediction using the Menelaus method alone, which is based on chronologic age.
Lampe and associates found that 9 of 30 patients treated by epiphysiodesis based on Moseley straight-line graph predictions had a discrepancy of more than 1.5 cm at skeletal maturity, including 1 patient operated on twice. These investigators concluded that the pattern of skeletal maturation limited the accuracy of the method. Beumer and colleagues, in a study of the growth of 182 Dutch children between 1979 and 1994, found that mean femoral and tibial length increased, compared with the data of Anderson and associates. Beumer and co-workers modified the Moseley straight-line graph based on this information and the use of skeletal age. Then, in a study of 34 patients treated by epiphysiodesis, these investigators found that the new graph better predicted limb length at maturity in 22 patients and yielded comparable results in 5 patients when predictions were made using the Moseley straight-line graph.
Carpenter and Lester evaluated skeletal age (according to Greulich and Pyle’s atlas) in the distal radius and ulna, carpus, and metacarpals and phalanges in 100 hand and wrist radiographs of 45 children younger than 10 years of age. These investigators found significant discrepancies between skeletal and chronologic age among the regions of the hand and between the sexes. Cundy and colleagues assessed variations in the designation of skeletal age in 60 radiographs by 4 radiologists who were using Greulich and Pyle’s atlas. These investigators found that 50% of children were assigned a skeletal age that differed by more than 1 year, and 10% varied by more than 2 years. As Ferron pointed out, the standard deviation of Greulich and Pyle’s atlas is “plus or minus one page.”
Before beginning treatment, the team should discuss again the various options, likely problems, and outcomes with the patient and family. This discussion is ideally conducted with a psychologist who works with children and is knowledgeable in orthopaedics. It is imperative that the child and family have considered their goal of the treatment and choose the medical intervention that is most suitable to them. Pros and cons of the leg lengthening procedure, as well as of alternative procedures, are reviewed. Outlining why the family is choosing the procedure and ensuring that leg lengthening is a priority to the child are necessary for moving forward.
Education is repeated by many medical team members. Asking the family what they know about the treatment and how they expect treatment to interfere with their daily lives and making sure that they understand that this is a high-maintenance procedure help the family prepare. Age-appropriate education for the child is key. The child is wearing the apparatus and will ultimately be the active participant in all aspects of the treatment. It is important to establish a plan for pain management, based on the child and family’s previous responses to pain and anxiety. Social support, the role of caretakers, and who will be responsible for the child’s follow-up and daily care should be established before the surgical procedure. All aspects of adherence, including pin care, lengthening, exercises, and follow-up appointments are emphasized in detail.
Psychological disorders, family support, pain tolerance and management, compliance with treatment, and the family’s goals of treatment can affect the treatment outcome. For example, if a child or family member has a significant, untreated mental health disorder, this may be exacerbated by the stress of a long, demanding treatment and may negatively affect the outcome. Based on pretreatment evaluation, a decision not to proceed may be made when there is a demonstrated inability to adhere to care and exercises, significant psychological disorders, family disharmony, and/or poor understanding of treatment, which would likely predict treatment failure.
During treatment, additional factors should be addressed to maximize successful outcome. These include coping with complications, sleep disturbance, returning to school, hospitalization, and patience with the process. These are monitored at each follow-up appointment, and interventions are tailored accordingly.
After the apparatus is removed, the child and family are reminded of continued adherence to treatment with regard to rehabilitation and activity restrictions. Transitioning from being a patient to being a child can be a challenge as well. Discontinuing pain medications with minimal side effects and addressing any issues of addiction are also aspects of this phase of care.
Subsequent lengthening procedures require more, not less, preoperative evaluation and education because the child often recalls the initial process being much easier than it actually was. The child is also at a different developmental age, which brings new issues into play.
Traditionally, orthopaedists have been taught that leg length inequality greater than 2 to 2.5 cm should be treated by some form of equalization. Based on a review of the literature, it is difficult to justify this figure as an absolute above which treatment is indicated. Between-leg discrepancies of more than 5% (corresponding to approximately 4 cm at skeletal maturity in 50th percentile patients) and the use of toe-walking to compensate for leg length inequality have been demonstrated in the gait laboratory to be associated with appreciable alterations in gait mechanism and energy consumption. Thus, this is certainly an absolute level above which limb length equalization by some means should be attempted. Treatment of lesser discrepancies in the absence of other deformities in the limb is based on considerably softer evidence of short- or long-term dysfunction in the individual patient. The wise orthopaedist carefully assesses the impact of leg length inequality in each patient, along with that person’s concerns regarding the inequality, to determine the best treatment. It is often helpful to have adolescents wear a shoe lift corresponding to 5 mm less than the actual discrepancy for a brief time to give them a sense of what correction will provide when the need for treatment is equivocal (usually in the 2- to 2.5-cm range). This can help the surgeon and the patient decide whether shortening or epiphysiodesis is indicated. Treatment options for the management of leg length inequality and indications for each are summarized in Table 20.5 .
| Treatment Option | Indications | Contraindications |
|---|---|---|
| No treatment | Discrepancies <2 cm | Shortening >5% of contralateral limb (4 cm) |
| Shoe lift | Consider for discrepancies >2 cm Recommended for toe-walkers |
None |
| Extension orthosis or prosthesis | Child who walks with extreme long-leg knee flexion, or one who hops | None |
| Epiphysiodesis | Predicted discrepancies >2 cm | As the sole means of correcting discrepancies >8 cm Inadequate growth remaining |
| Epiphyseal stapling | Same as epiphysiodesis | Same as epiphysiodesis |
| Acute surgical shortening | Skeletally mature patient Femoral discrepancy 2–5 cm Tibial discrepancy 2–3 cm |
Discrepancies requiring >6 cm of femoral or >5 cm of tibial shortening |
| Acute surgical lengthening | Femoral discrepancy 2–4 cm Tibial discrepancy 2–3 cm |
Patients at risk for neurovascular injury or with poor bone quality |
| Gradual limb lengthening | Femoral discrepancy >4 cm Leg length inequality associated with angular deformity requiring correction |
Unstable joints associated with bone segment to be lengthened Noncompliant patient |
In theory, any leg length inequality can be managed with a lift of appropriate size applied to the sole or within the shoe. Interestingly, only rarely is this approach acceptable to the patient as a long-term solution, and the child and parents are almost always willing to proceed with any appropriate surgical procedure that obviates the use of a lift.
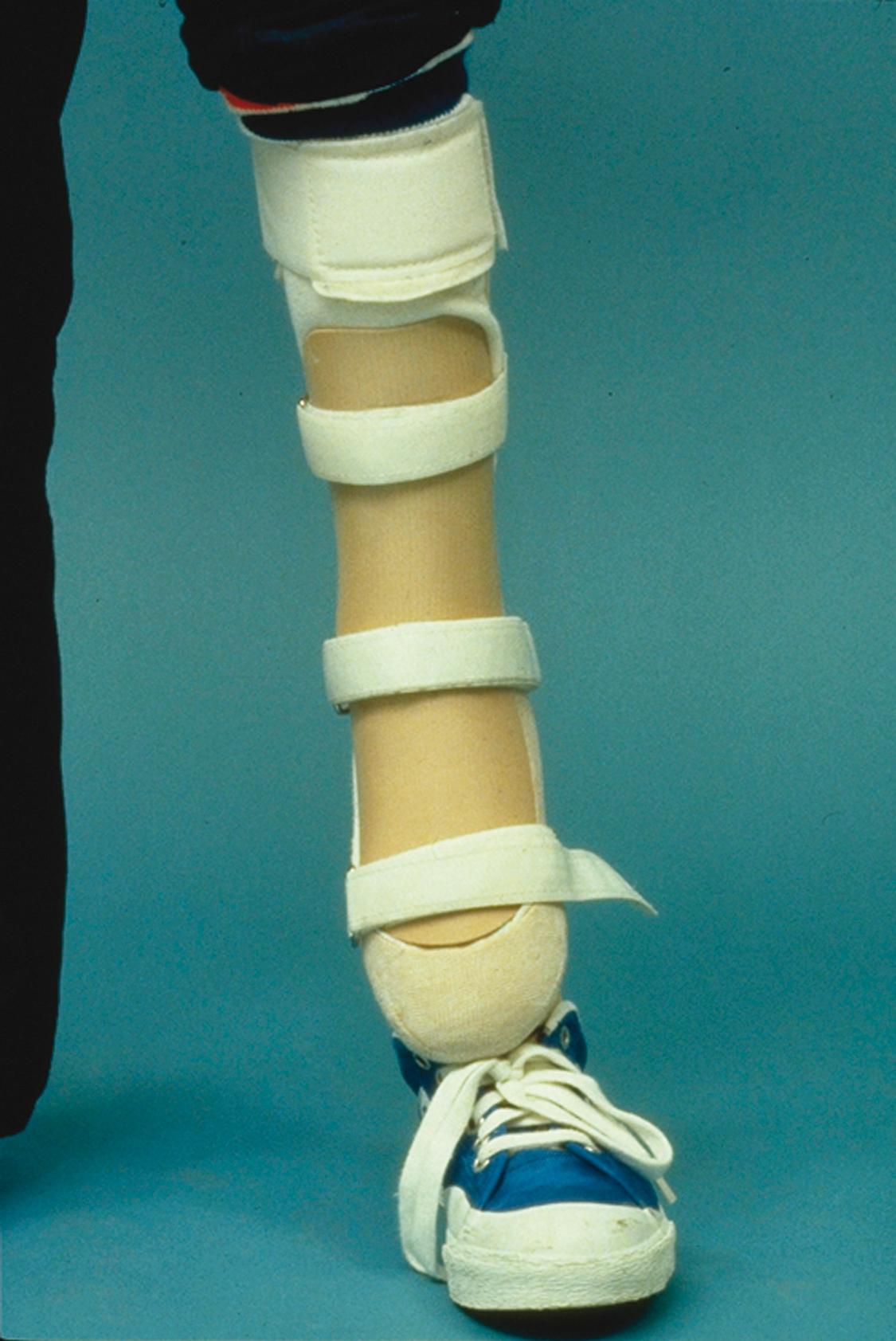
The indications for the use of a shoe lift, even in the short term, are not clear-cut and are controversial. Little evidence indicates that the use of a shoe lift provides any short- or long-term protective or mechanical benefits. , , , , We consider a lift when a child begins to toe-walk, which is usually when leg length inequality reaches 5% of the contralateral side, because at this point, increased work of the long leg has been documented. Lifts of up to 1 cm can be incorporated into most shoes; larger lifts do not allow the child to wear the shoe comfortably and must be applied to the sole of the shoe. Once the child is compensating for leg length inequality by toe-walking and other strategies such as vaulting, circumducting, or increased flexion of the long leg, we consider not only a lift but an orthosis as well. Lifts greater than 8 cm are not easy for patients to manage and may cause them to fall over or sprain their ankles ( Fig. 20.20 ). The addition of an ankle-foot orthosis can be helpful in such circumstances. If the child is actually hopping on the longer leg because the shorter leg is not reaching the floor, an extension orthosis can improve gait significantly. This orthosis is a combination of a suspension component (an ankle-foot orthosis, usually set in equinus, with an anterior shell or, more commonly, a knee-ankle-foot orthosis) and a shank terminating in a solid ankle-cushioned heel prosthetic foot. This allows the patient to ambulate with a level pelvis and wear a normal shoe ( Fig. 20.21 ).

There are a number of ways of shortening the longer extremity in a growing individual. These include permanent growth arrest, or epiphysiodesis, and temporary growth arrest by epiphyseal stapling or plating. In the mature person, long-bone shortening is used.
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here