Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
The urge to prognosticate following trauma is as old as the practice of medicine. This is not surprising, because injured patients and their families wish to know if death is likely, and physicians have long had a natural concern not only for their patients’ welfare but for their own reputations. Today there is a growing interest in tailoring patient referral and physician compensation based on outcomes, outcomes that are often measured against patients’ likelihood of survival. Despite this enduring interest, the actual measurement of human trauma began only 50 years ago when DeHaven’s investigations into light plane crashes led him to attempt the objective measurement of human injury. Although we have progressed far beyond DeHaven’s original efforts, injury measurement and outcome prediction are still in their infancy, and we are only beginning to explore how such prognostication might actually be employed.
In this chapter, we examine the problems inherent in injury measurement and outcome prediction, and then recount briefly the history of injury scoring, culminating in a description of the current de facto standards: the Injury Severity Score (ISS), the Revised Trauma Score (RTS), and their synergistic combination with age and injury mechanism into the Trauma and Injury Severity Score (TRISS). We will then examine the shortcomings of these methodologies and discuss newer scoring approaches that have been proposed as improvements. Finally, we will speculate on how good prediction can be and to what uses injury severity scoring should be put given these constraints. We will find that the techniques of injury scoring and outcome prediction have little place in the clinical arena and have been oversold as means to measure quality. They remain valuable as research tools, however.
Injury scoring is a process that reduces the myriad complexities of a clinical situation to a single number. In this process, information is necessarily lost. What is gained is a simplification that facilitates data manipulation and makes objective prediction possible. The expectation that prediction accuracy will necessarily be improved by scoring systems is unfounded; however, when intensive care unit (ICU) scoring systems have been compared with clinical acumen, the clinicians usually perform better.
Clinical trauma research is made difficult by the seemingly infinite number of possible anatomic injuries, and this is the first problem we must confront. Injury description can be thought of as the process of subdividing the continuous landscape of human injury into individual, well-defined injuries. Fortunately for this process, the human body tends to fail structurally in consistent ways. Le Fort discovered that the human face usually fractures in only three patterns despite a wide variety of traumas, and this phenomenon is true for many other parts of the body. The common use of eponyms to describe apparently complex orthopedic injuries underscores the frequency with which bones fracture in predictable ways. Nevertheless, the total number of possible injuries is large. The Abbreviated Injury Scale (AIS) is now in its ninth edition and includes descriptions of more than 2000 injuries (increased from 1395 in AIS 1998). The International Classification of Diseases (ICD), 10th Revision (ICD-10) also devotes over 1000 codes to injuries. Moreover, most specialists could expand by severalfold the number of possible injuries. However, a scoring system detailed enough to satisfy all specialists would be so demanding in practice that it would be impractical for nonspecialists. Injury dictionaries thus represent an unavoidable compromise between clinical detail and pragmatic application.
It is perhaps surprising that two entirely separate lexicons exist to describe individual traumatic injuries. Although both the AIS and ICD have long histories; they arose in response to very different needs. The ICD was intended to create a finite number of categories that encompassed all possible morbid conditions. The AIS, by contrast, was designed to include only injuries, and further, to assign a general measure of severity (1–6) for each injury. Because AIS was created specifically to describe injuries, it might seem a more natural lexicon to employ in trauma scoring. However, the ubiquity of ICD coding has proved irresistible, and currently both AIS and ICD lexicons are used in the description of human trauma. The existence of two competing systems for recording injuries complicates both injury scoring and the comparison of scoring results because the lexicons are so deeply incompatible that no unambiguous matching can be constructed to translate between AIS and ICD. Because ICD codes are routinely collected, and thus have an effective collection cost of zero, it is possible that, despite its shortcomings, ICD coding will displace the modestly more expensive AIS system over time.
Although an “injury” is usually thought of in anatomic terms, physiologic injuries at the cellular level, such as hypoxia or hemorrhagic shock, is important. Not only does physiologic impairment figure prominently in the injury description process used by emergency paramedical personnel for triage, but such descriptive categories are crucial if injury description is to be used for accurate prediction of outcome. Thus, the outcome after splenic laceration hinges more on the degree and duration of hypotension than on degree of structural damage to the spleen itself. Because physiologic injuries are by nature evanescent, changing with time and therapy, reliable capture of this type of data can be challenging.
The ability to describe injuries consistently on the basis of a single descriptive dictionary guarantees that similar injuries will be classified as the same. However, in order to compare different injuries, a scale of severity is required. Severity is usually interpreted as the likelihood of a fatal outcome; however, length of stay in an ICU, length of hospital stay, extent of disability, or total expense that is likely to be incurred could each be considered measures of severity as well.
In the past, severity measures for individual injuries have generally been assigned by experts. Ideally, however, these values should be objectively derived from injury-specific data. Importantly, the severity of an injury may vary with the outcome that is being contemplated. Thus, a gunshot wound to the aorta may have a high severity when mortality is the outcome measure, but a low severity when disability is the outcome measure. (That is, if the patient survives, he or she is likely to recover quickly and completely.) A gunshot wound to the femur might be just the reverse in that it infrequently results in death but often causes prolonged disability.
Although it is a necessary first step to rate the severity of individual injuries, comparisons between patients or groups of patients are of greater interest. Because patients typically have more than a single injury, the severity of several individual injuries must somehow be combined to produce a single overall measure of injury severity. Although several mathematical approaches of combining separate injuries into a single score have been proposed, it is uncertain which of these formulas is most correct. The severity of the single worst injury, the product of the severities of all the injuries a patient has sustained, and the sum of the squared values of severities of a few of the injuries a patient has sustained have all been proposed, and other schemes are likely to emerge. The problem is made still more complex by the possibility of interactions between injuries. We will return to this fundamental but unresolved issue later.
As noted, anatomic injury is not the sole determinant of survival. Physiologic derangement and patient reserve also play crucial roles. A conceptual expression to describe the role of anatomic injury, physiologic injury, and physiologic reserve in determining outcome might be stated as follows:
Our task is thus twofold: First, we must define summary measures of anatomic injury, physiologic injury, and patient reserve. Second, we must devise a mathematical expression combining these predictors into a single prediction of outcome, which for consistency will always be an estimated probability of survival. We will consider both of these tasks in turn. However, before we can consider various approaches to outcome prediction, we must briefly discuss the statistical tools that are used to measure how well predictive models succeed in the tasks of measuring injury severity and in separating survivors from nonsurvivors.
We will discuss a group of the most widely used measures of anatomic injury, physiologic injury, and patient reserve, as well as combinations of them ( Table 1 ). We will then compare the predictive accuracy of these measures by category using the 2017 U.S. National Trauma Data Bank (NTDB).
| Type of Score | Score | Values Range | Origin |
|---|---|---|---|
| Anatomic | Abbreviated Injury Scale (AIS) | 1–6 | CMAAS, 1971 |
| Injury Severity Score (ISS) | 0–75 | Baker et al., 1974 | |
| Anatomic Profile Score (APS) | 0–12 | Copes et al., 1990 | |
| ICD-based injury severity score (ICISS) | 0–1 | Osler et al., 1996 | |
| New Injury Severity Score (NISS) | 0–75 | Osler et al., 1997 | |
| Trauma Mortality Prediction Model (TMPM) * | 0–1 | Osler et al., 2008 | |
| Physiologic | Shock Index (SI) | 0–∞ | Allgower and Burric, 1967 |
| Glasgow Coma Scale (GCS) | 3–15 | Teasdale and Jennet, 1974 | |
| Acute Trauma Index (ATI) | 0–9 | Milholland et al., 1979 | |
| Revised Trauma Score (RTS) | 0–7.84 | Champion et al., 1989 | |
| New Trauma Score (NTS) | 1.2 – 10.7 | Jeong et al., 2017 | |
| Combined | Trauma and Injury Severity Score (TRISS) | 0–1 | Champion and Sacco, 1983 |
| A Severity Characterization of Trauma (ASCOT) | 0–1 | Champion et al., 1990 | |
| Kampala Trauma Score (KTS) | 5–16 | Owar and Kobusingye, 2001 | |
| Mechanism, GCS, Age, and SBP (MGAP) | 3–29 | Baghi et al., 2015 | |
| Physiologic reserve | Charlson Comorbidity Index (CCI) | 0–37 | Charlson et al., 1987 |
| Elixhauser Comorbidity Index (ECI) | 0–89 | Elixhauser et al., 1998 | |
| Acute Physiology and Chronic Health Evaluation (APACHE) † | 0–71 | Knaus et al., 1981 |
* TMPM can be computed with both ICD and AIS lexicons.
† APACHE has multiple versions (I–IV); version II is most widely used.
Most clinicians are comfortable with the concepts of sensitivity and specificity when considering how well a laboratory test predicts the presence or absence of a disease. Sensitivity and specificity are inadequate for the thorough evaluation of tests, however, because they depend on an arbitrary cut-point to define “positive” and “negative” results. A better overall measure of the discriminatory power of a test is the area under the receiver operating characteristic (ROC) curve, often abbreviated as AUC (area under the curve). Formally defined as the area beneath a graph of sensitivity (true-positive proportion) graphed against 1 – specificity (false-positive proportion), the AUC can perhaps more easily be understood as the proportion of correct discriminations a test makes when confronted with all possible comparisons between diseased and nondiseased individuals in the data set. In other words, imagine that a survivor and a nonsurvivor are randomly selected by a blindfolded researcher, and the scoring system of interest is used to try to pick the survivor. If we repeat this trial many times (e.g., 10,000 or 100,000 times), the area under the ROC curve will be the proportion of correct predictions. Thus, a perfect test that always distinguishes a survivor from a nonsurvivor correctly has an AUC of 1, whereas a useless test that picks the survivor no more often than would be expected by chance alone has an AUC of 0.5.
A second salutary property of a predictive model is that it has clarity of classification. That is, if a rule classifies a patient with an estimated chance of survival of 0.5 or greater to be a survivor, then ideally the model should assign survival probabilities near 0.5 to as few patients as possible and values close to 1 (death) or 0 (survival) to as many patients as possible. A rule with good discriminatory power will typically have clarity of classification for a range of cutoff values.
A final property of a good scoring system is that it is well calibrated; that is, it performs consistently throughout its entire range, with 50% of patients with a 0.5 predicted mortality actually dying, and 10% of patients with a 0.1 predicted mortality actually dying. Although this is a convenient property for a scoring system to have, it is not a measure of the actual predictive power of the underlying model and predictor variables. In particular, a well-calibrated model does not have to produce more accurate predictions of outcome than a poorly calibrated model. Calibration is best thought of as a measure of how well a model fits the data, rather than how well a model actually predicts outcome.
Calibration is commonly evaluated using the Hosmer-Lemeshow (HL) statistic. This statistic is calculated by first dividing the data set into 10 equal deciles (by count or value) and then comparing the predicted number of survivors in each decile to the actual number of survivors. The result is evaluated as a chi-square test. A low value for the HL statistic (corresponding to a high p value) implies that the model is well calibrated. Unfortunately, the HL statistic is sensitive to the size of the data set, with very large data sets uniformly being declared “poorly calibrated.” Conversely, if the number of possible predictive categories is small (< 6), the HL statistic will almost always find that a model is “well calibrated.” Finally, the creators of the HL statistic have noted that its actual value may depend on the arbitrary groupings used in its calculation, and this further diminishes the HL statistic’s appeal as a general measure of calibration.
In sum, the ROC curve area is a measure of how well a model distinguishes survivors from nonsurvivors, whereas the HL statistic is a measure of how carefully a model has been mathematically fitted to the data. In the past, the importance of the HL statistic has been overstated and even used to commend one scoring over another. This represents a fundamental misapplication of the HL statistic. Overall, we believe less emphasis should be placed on the HL statistic.
In practice, however, we often wish to compare two or more models rather than simply examine the performance of a single model. The procedure for model selection is a sophisticated statistical enterprise that has not yet been widely applied to trauma outcome models. One promising avenue is an information theoretical approach in which competing models are evaluated based on their estimated distance from the true (but unknown) model in terms of information loss. Although it might seem impossible to compare distances to an unknown correct model, such comparisons can be accomplished by using the Akaike information criterion (AIC) and related refinements.
For example, the development of the Trauma Mortality Prediction Model (TMPM), based on International Classification of Diseases codes, has been described by Osler et al. When compared with ISS, the TMPM-ICD10 discriminated survivors from nonsurvivors better based on ROC (ROC TMPM-ICD10 = 0.861 [0.860–0.872], ROC ISS = 0.830 [0.823–0.836]), was better calibrated based on HL statistic (HL TMPM-ICD10 = 49.01, HL ISS = 788.79), and had a lower AIC, demonstrating better estimated distance from a true model (AIC TMPM-ICD10 = 30579.49; AIC ISS = 31802.18). This demonstrates that TMPM-ICD10 could replace ISS as the standard measure of overall injury severity for data coded in the ICD-10-CM lexicon.
Two practical aspects of outcome model building and testing are particularly important. First, a model based on a data set usually performs better when it is used to predict outcomes for that data set than for other data sets. This is not surprising, because any unusual features of that data set will have been incorporated, at least partially, into the model under consideration. The second, more subtle, point is that the performance of any model depends on the data evaluated. A data set consisting entirely of straightforward cases (i.e., all patients are either trivially injured and certain to survive or overwhelmingly injured and certain to die) will make any scoring system seem accurate. But a data set in which every patient is gravely but not necessarily fatally injured is likely to cause the scoring system to perform no better than chance. Thus, when scoring systems are being tested, it is important first that they be developed in unrelated data sets and second that they be tested against data sets typical of those expected when the scoring system is actually used. This latter requirement makes it extremely unlikely that a universal equation can be developed, because factors not controlled for by the prediction model are likely to vary among trauma centers.
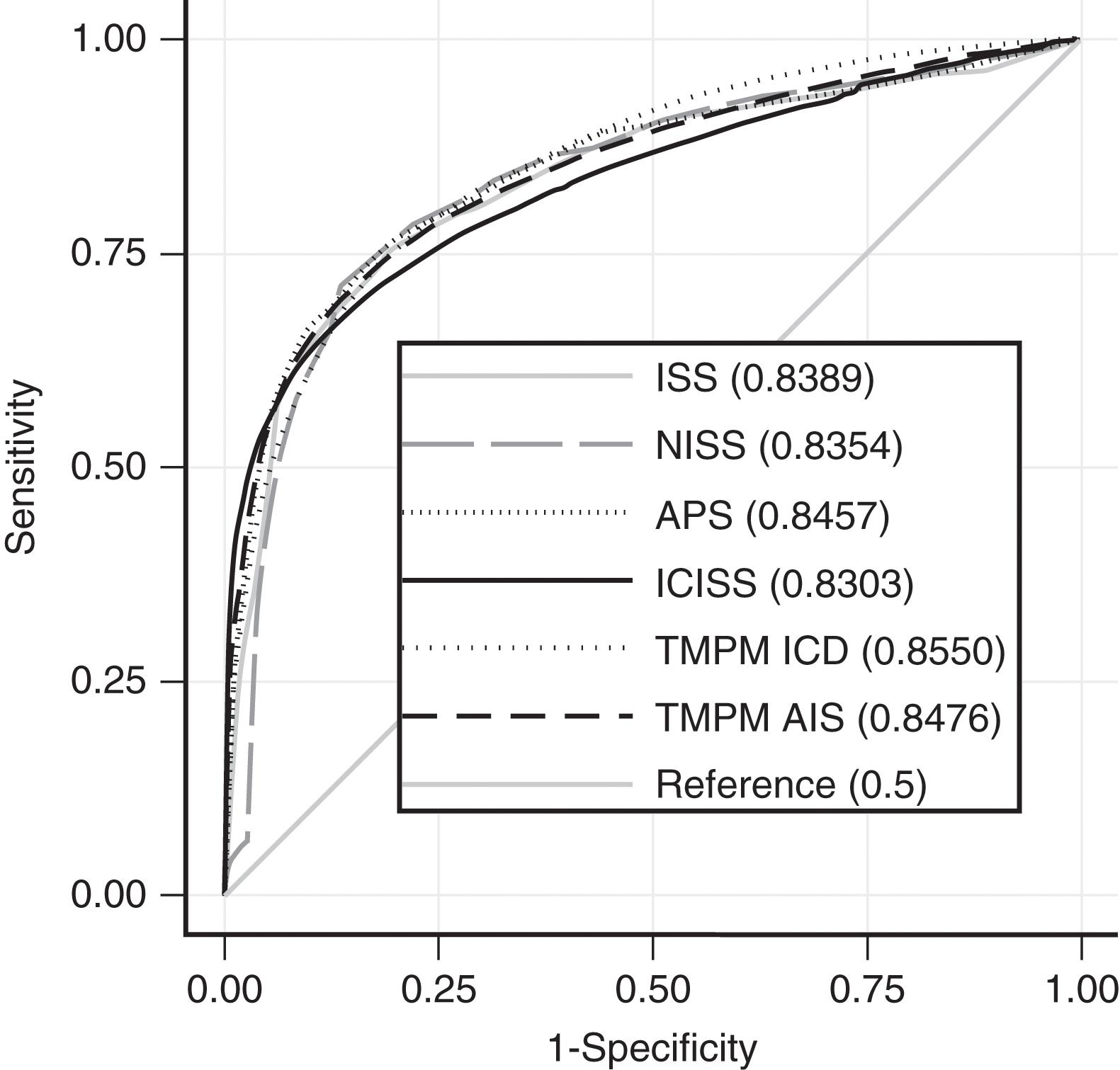
Measurement of anatomic injury requires first a dictionary of injuries, second a severity for each injury, and finally a rule for combining multiple injuries into a single severity score. The first two requirements were addressed in 1971 with the publication of the first AIS manual. Although this initial effort included only 73 general injuries and did not address penetrating trauma, it did assign a severity to each injury ranging from 1 (minor) to 6 (fatal). No attempt was made to create a comprehensive list of injuries, and no mechanism to summarize multiple injuries into a single score was proposed. However, a number of anatomic injury scores have been proposed and are in use today with relatively similar predictive power and calibration ( Table 2 ).
| Anatomic Injury Scores | AUROC (95% CI) | AIC |
|---|---|---|
| Injury Severity Score (ISS) | .8389 (.8414–.8365) | 240156.28 |
| Anatomic Profile Score (APS) | .8457 (.8482–.8433) | 229158.00 |
| ICD-based injury severity score (ICISS) | .8303 (.8329–.8277) | 226642.76 |
| New Injury Severity Score (NISS) | .8354 (.8377–.8330) | 280091.64 |
| Trauma Mortality Prediction Model (TMPM)—ICD | .8550 (.8571–.8529) | 239476.23 |
| Trauma Mortality Prediction Model (TMPM)—AIS | .8476 (.8501–.8452) | 204994.77 |
This inability to summarize multiple injuries occurring in a single patient soon proved problematic and was addressed by Baker and colleagues in 1974 when they proposed the ISS. This score was defined as the sum of the squares of the highest AIS grade in each of the three (of six) most severely injured body areas:
Because each injury was assigned an AIS severity from 1 to 6, the ISS could assume values from 0 (uninjured) to 75 (severest possible injury). A single AIS severity of 6 (fatal injury) resulted in an automatic ISS of 75. This scoring system was tested in a group of 2128 automobile accident victims. Baker and colleagues concluded that 49% of the variability in mortality rate was explained by this new score, a substantial improvement over the 25% explained by the previous approach of using the single worst-injury severity.
Both the AIS dictionary and the ISS have enjoyed considerable popularity over the past 30 years. Each injury in this dictionary is assigned a severity from 1 (slight) to 6 (unsurvivable), as well as a mapping to the Functional Capacity Index (a quality-of-life measure). The ISS has enjoyed even greater success—it is virtually the only summary measure of trauma in clinical or research use and has not been modified in the 30 years since its inception.
Despite these past successes, both the AIS dictionary and the ISS have substantial shortcomings. The problems with AIS are twofold. First, the severities for each of the injuries are consensus derived from committees of experts and not simple measurements. Although this approach was necessary before large databases of injuries and outcomes were available, it is now possible to accurately measure the severity of injuries on the basis of actual outcomes. Such calculations are not trivial, however, because patients typically have more than a single injury, and untangling the effects of individual injuries is a significant mathematical exercise. Using measured severities for injuries would correct the inconsistent perceptions of severity of injury in various body regions first observed by Beverland and Rutherford and later confirmed by Copes et al. A second difficulty is that AIS scoring is expensive and therefore is done only in hospitals with a zealous commitment to trauma. As a result, the experiences of most nontrauma center hospitals are excluded from academic discourse, thus making accurate demographic trauma data difficult to obtain.
The ISS has several undesirable features that result from its ad hoc conceptual underpinnings. First, because it depends on the AIS dictionary and severity scores, the ISS is heir to all the difficulties outlined previously. But the ISS is also intrinsically problematic in several ways. By design, regardless of how many injuries a patient may have sustained, the ISS allows a maximum of three injuries to contribute to the final score, but the actual number allowed is often fewer. Moreover, because the ISS allows only one injury per body region to be scored, the scored injuries are often not even the three most severe injuries. By considering less severe injuries, ignoring more severe injuries, and ignoring many injuries altogether, the ISS loses considerable information. Baker herself proposed a modification of the ISS, the New ISS (NISS), which was computed from the three worst injuries (highest AIS), regardless of the body region in which they occurred. Surprisingly, the NISS does not improve substantially upon the discrimination of ISS; however, it does more accurately predict complications and mortality.
Additionally, the ISS is not felt to accurately reflect outcomes for pediatric trauma. In this patient population, clinicians use the Modified Injury Severity Score (MISS). This system categorizes the body into five areas instead of nine. These five regions are neurologic, face and neck, chest, abdomen and pelvic contents, and extremities and pelvic girdle. The MISS is calculated using the sum of the squares of the three most severely injured body regions. A MISS of greater than or equal to 25 is an accurate predictor of mortality and morbidity.
The ISS is also problematic mathematically. Although it is usually handled statistically as a continuous variable, the ISS can assume only integer values. Further, although its definition implies that the ISS can at least assume all integer values throughout its range of 0 to 75, because of its curious “sum-of-one (or two or three) squared integers” construction, many integer values can never occur. For example, 7 is not the sum of any three squares, and therefore can never be an ISS value. In fact, only 44 of the values in the range of ISS can be valid ISS values, and half of these are concentrated between 0 and 26. As a final curiosity, some ISS values are the result of one, two, or as many as 28 different AIS combinations. Overall, the ISS is perhaps better thought of as a procedure that maps the 84 possible combinations of three or fewer AIS injuries into 44 possible scores that are distributed between 0 and 75 in a nonuniform way.
The consequences of these idiosyncrasies for the ISS are severe, as an examination of the actual mortality rate for each of 44 ISS scores in a large data set (based on 997,970 patients from the 2017 NTDB) demonstrates. Mortality does not increase smoothly with increasing ISS, and more troublingly, for many pairs of ISS scores, the higher score is actually associated with a lower mortality rate ( Fig. 1 A and B). Some of these disparities are striking: patients with ISS values of 27 are four times less likely to die than patients with ISS values of 25. This anomaly occurs because the injury subscore combinations that result in an ISS of 25 (5, 0, 0 and 4, 3, 0) are, on average, more likely to be fatal than the injury subscore combinations that result in an ISS of 27 (5, 1, 1 and 3, 3, 3). Kilgo et al. note that 25% of ISSs can actually be the result of two different subscore combinations, and that these subscore combinations usually have mortality rates that differ by over 20%.
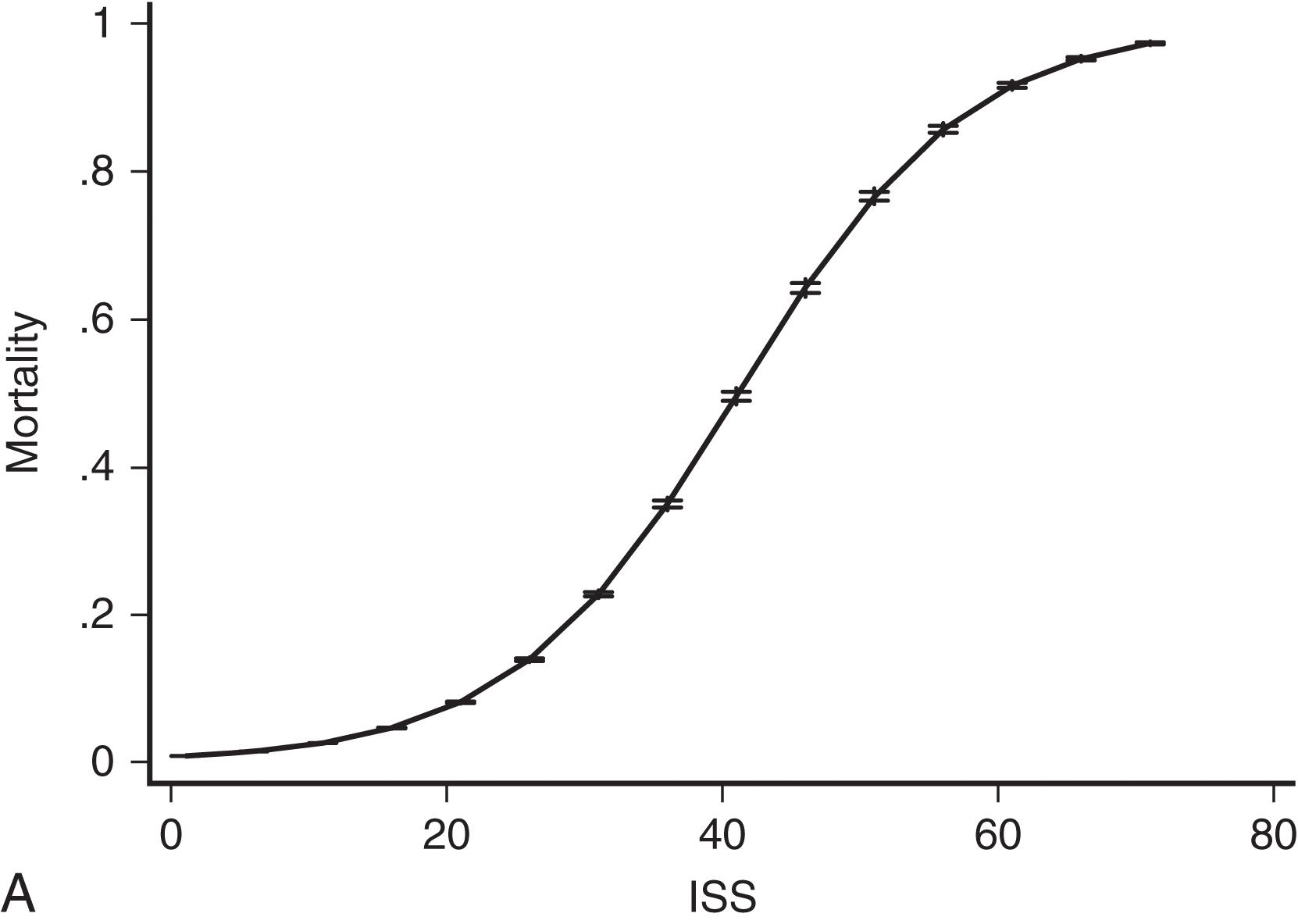
Despite these problems, the ISS has remained the preeminent scoring system for trauma. In part this is because it is widely recognized and easily calculated, and it provides a rough ordering of severity that has proved useful to researchers. Moreover, the ISS does powerfully separate survivors from nonsurvivors, as matched histograms of ISS for survivors and fatalities in the NTDB demonstrate ( Fig. 1 B), with an ROC of 0.84 ( Table 1 ).
The idiosyncrasies of ISS have prompted investigators to seek better and more convenient summary measures of injury. Champion and coworkers attempted to address some of the shortcomings of ISS in 1990 with the Anatomic Profile (AP), later modified to become the modified AP (mAP). The AP used the AIS dictionary of injuries and assigned all AIS values greater than 2 to one of three newly defined body regions (head/brain/spinal, thorax/neck, other). Injuries were combined within a body region using a Pythagorean distance model, and these values were then combined as a weighted sum. Although the discrimination of the AP and mAP improved upon the ISS, this success was purchased at the cost of substantially more complicated calculations, and the AP and mAP have not seen wide use.
Osler and coworkers in 1996 developed an injury score based upon the ICD-9 lexicon of possible injuries. Dubbed ICISS (ICD-9 Injury Severity Score), the score was defined as the product of the individual probabilities of survival for each injury a patient sustained:
where SRR = survival risk ratio.
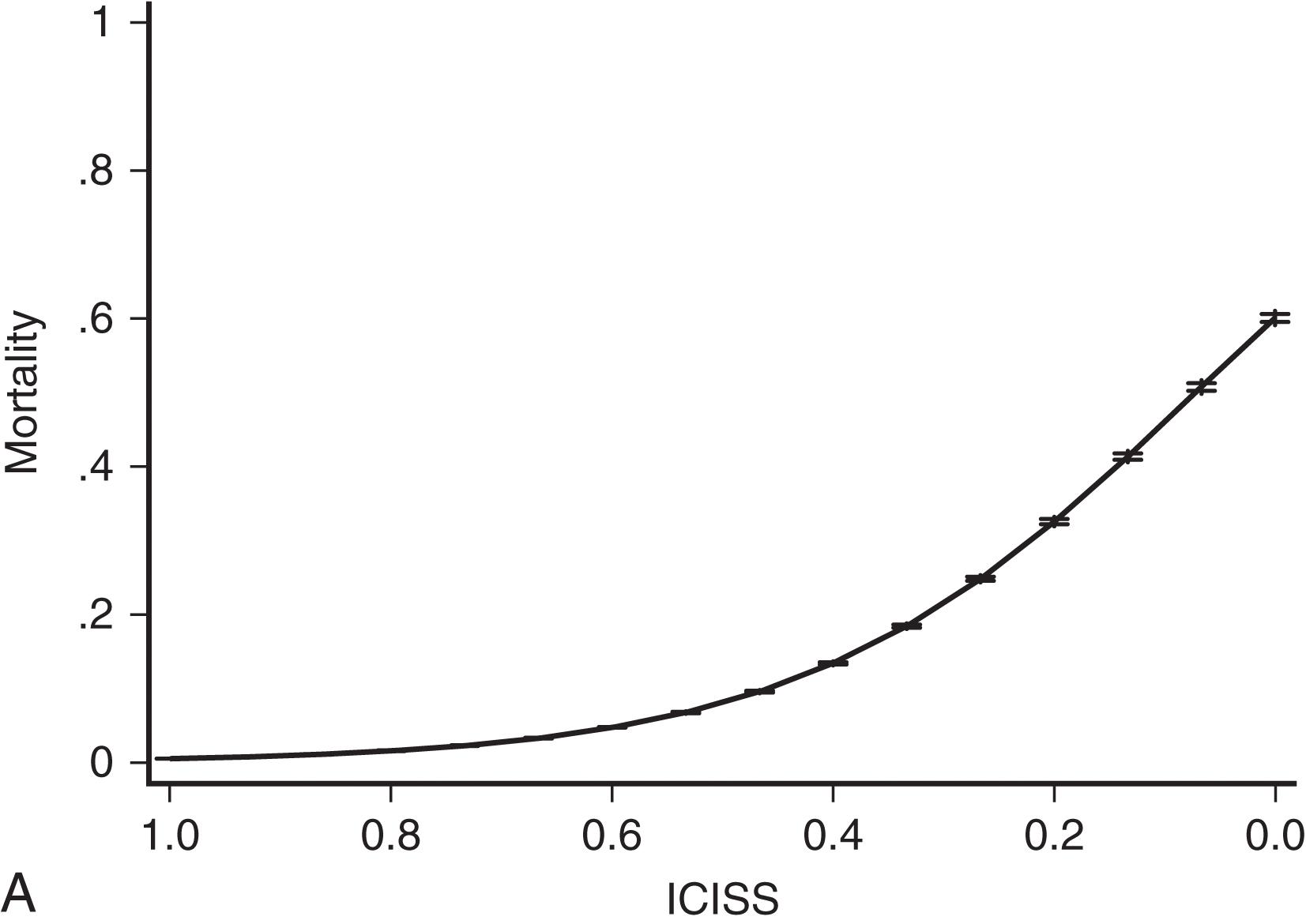
These empiric survival risk ratios were in turn calculated from a large trauma database. ICISS was thus by definition a continuous predictor bounded between 0 and 1. ICISS provided better discrimination between survivors and nonsurvivors than did ISS and also proved better behaved mathematically. The probability of death uniformly decreases as ICISS increases ( Fig. 2 A), and ICISS powerfully separates survivors from nonsurvivors ( Fig. 2 B). A further advantage of the ICISS is that it can be calculated from administrative hospital discharge data, and thus the time and expense of AIS coding are avoided. This coding convenience has the salutary effect of allowing the calculation of ICISS from administrative data sets and thus allows injury severity scoring for all hospitals.
Other ICD-based scoring schemes have been developed that first map ICD descriptors into the AIS lexicon and then calculate AIS-based scores (such as ISS or AP). In general, power is lost with such mappings because they are necessarily imprecise, and thus this approach is only warranted when AIS-based scores are needed but only ICD descriptors are available.
Many other scores have been created. Perhaps the simplest was suggested by Kilgo and coworkers, who noted that the survival risk ratio for the single worst injury was a better predictor of fatality than several other models they considered that used all the available injuries. This observation is very interesting because it seems unlikely that ignoring injuries should improve a model’s performance. Rather, Kilgo’s observation seems to imply that most trauma scores are miss-specified; that is, they use the information present in the data suboptimally. Much more complex models, some based on exotic mathematical approaches such as neural networks and classification and regression trees, have also been advocated but have failed to improve the accuracy of predictions.
To evaluate the performance of various anatomic injury models, their discrimination and calibration must be compared using a common data set. The largest such study was performed by Meredith et al., who evaluated nine scoring algorithms using the 76,871 patients then available in the NTDB. Performance of the ICISS and AP were found to be similar, although ICISS better discriminated survivors from nonsurvivors, and the AP was better calibrated. Both of these more modern scores dominated the older ISS, however. Meredith and colleagues concluded that “ICISS and APS [Anatomic Profile Score] provide improvement in discrimination relative to .... ISS. Trauma registries should move to include ICISS and the APS. ... The ISS performed moderately well and [has] bedside benefits.”
Because both ICD and AIS continue to be used to describe traumatic injuries, a scoring approach that can produce predictions based on either lexicon seems desirable. Only one such model is currently available, the Trauma Mortality Prediction Model (TMPM). TMPM is based on a derived empirical severity value for each ICD or AIS code using model-averaged regression coefficients. TMPM provides better calibration and discrimination compared with ISS, NISS, and ICISS. However, there is a tendency to overestimate the severity of the injury with TMPM. We have described and compared the most widely used anatomic trauma severity scores, their calibration ( Table 2 ), and their predictive accuracy and power ( Fig. 3 ).
Although the goal of many trauma scoring systems is to determine morbidity and mortality of a multitrauma patient, it does not always accurately reflect the isolated trauma patient. For example, patients with isolated penetrating trauma to the abdomen may be misrepresented by the ISS. Moore et al. recognized this in the early 1980s and created the Penetrating Abdominal Trauma Index. This uses a scoring system similar to the ISS, but specific to abdominal trauma, to quantify risk of complication following penetrating injury. However, while this scoring system was able to determine patients at risk for complications, it was limited by failing to account for patient age and physiologic parameters.
Many of the severity scoring systems are limited in clinical application because they are difficult to compute in time pressure, are dependent on diagnoses, and are mainly retrospectively applied; thus, they are not used to guide management. However, the Mangled Extremity Severity Score is an example where injury scoring can guide management. Using a clinically validated risk stratification tool, clinicians can address the likelihood of limb salvage in trauma patients. This is an example where isolated injury scoring systems have excelled in guiding management as the Mangled Extremity Severity Score is routinely used throughout the country and is still valid years after its development.
Accurate outcome prediction depends on more than simply reliable anatomic injury severity scoring. If we imagine two patients with identical injuries (e.g., four contiguous comminuted rib fractures and underlying pulmonary contusion), we would predict an equal probability of survival until we are informed that one patient is breathing room air comfortably while the other is dyspneic on a 100% O 2 rebreathing mask and has a respiratory rate of 55. Although the latter patient is not certain to die, his chances of survival are certainly lower than those of the patient with a normal respiratory rate. Although obvious in clinical practice, quantification of physiologic derangement has been challenging.
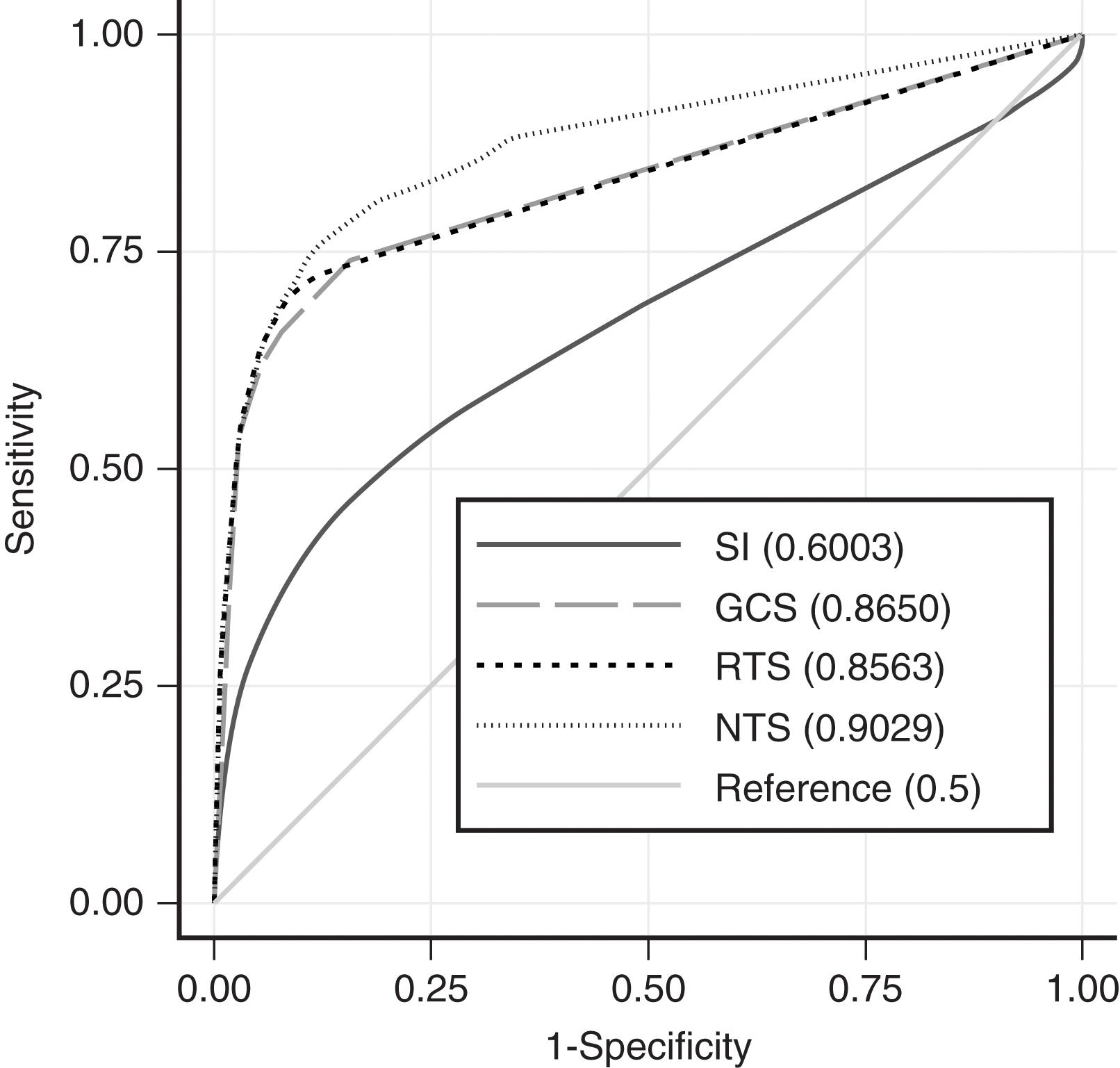
Basic physiologic measures such as blood pressure and pulse have long been important in the evaluation of trauma victims. Shock was described in 1862 by Samuel Gross as the “rude unhinging of the machinery of life.” One of the first severity scores was termed the Shock Index (SI) by Allgower and Burric in 1969. The Shock Index (SI), defined as heart rate (beats per minute) divided by systolic blood pressure (SBP) (mm Hg), has been proposed as a simple and useful indicator of early life-threatening shock in injured patients. The simplicity of this hemodynamic parameter makes it easily obtainable at the bedside. Allgower and Burric showed that an SI greater than or equal to 1.0 was associated with 40% mortality. Despite this, SI demonstrates poor predictive power (area under the ROC curve [AUROC] 0.60) (see Table 3 and Fig. 6 ).
| Physiologic Injury Scores | AUROC (95% CI) | AIC |
|---|---|---|
| Shock Index (SI) | .6003 (.5961–.6045) | 239387.4 |
| Glasgow Coma Scale (GCS) | .8650 (.8673–.8627) | 196586.88 |
| Revised Trauma Score (RTS) | .8563 (.8587–.8539) | 178199.66 |
| New Trauma Score (NTS) | .9029 (.9054–.9005) | 120582.78 |
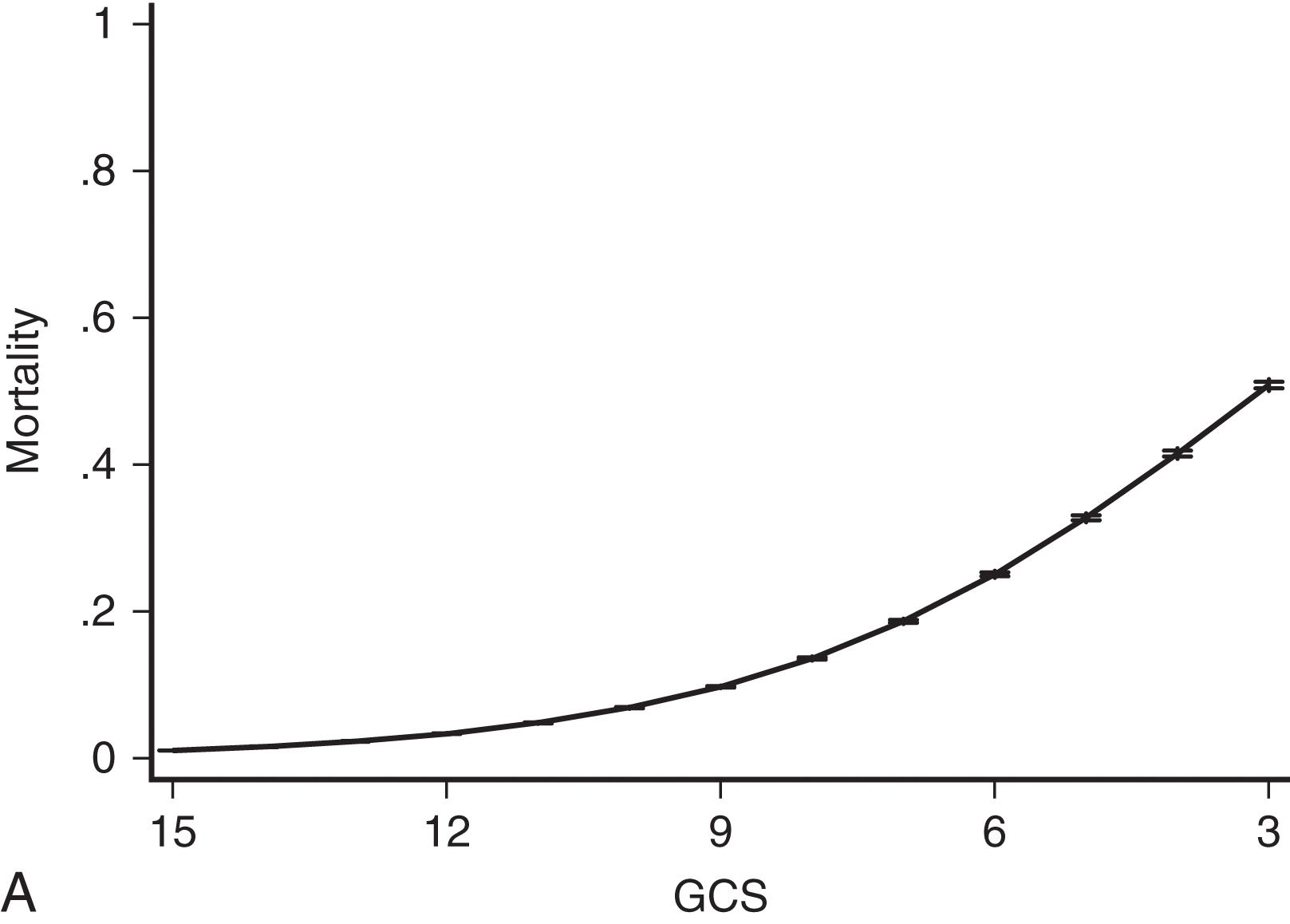
More recently, the Glasgow Coma Scale (GCS) has been added to the routine trauma physical examination ( Fig. 4 A). Originally conceived over 30 years ago as measure of the “depth and duration of impaired consciousness and coma,” the GCS is defined as the sum of coded values that describe a patient’s motor (1–6), verbal (1–5), and eye (1–4) levels of response to speech or pain. As defined, the GCS can take on values from 3 (unresponsive) to 15 (unimpaired). Unfortunately, simply summing these components obscures the fact that the GCS is actually the result of mapping the 120 different possible combinations of motor, eye, and verbal responses into 12 different scores. The result is a curious triphasic score in which scores of 7, 8, 9, 10, and 11 have identical mortality probabilities. Fortunately, almost all of the predictive power of the GCS is present in its motor component, which has a very nearly linear relationship to survival ( Fig. 4 B). It is likely that the motor component alone could replace the GCS with little or no loss of performance, and it has the clear advantage that such a score could be calculated for intubated patients, something not possible with the three-component GCS because of its reliance on verbal response. Despite these imperfections, the GCS remains part of the trauma physical examination, perhaps because as a measure of brain function , the GCS assesses much more than simply the anatomic integrity of the brain. Figure 4 C shows that GCS powerfully separates survivors from nonsurvivors.
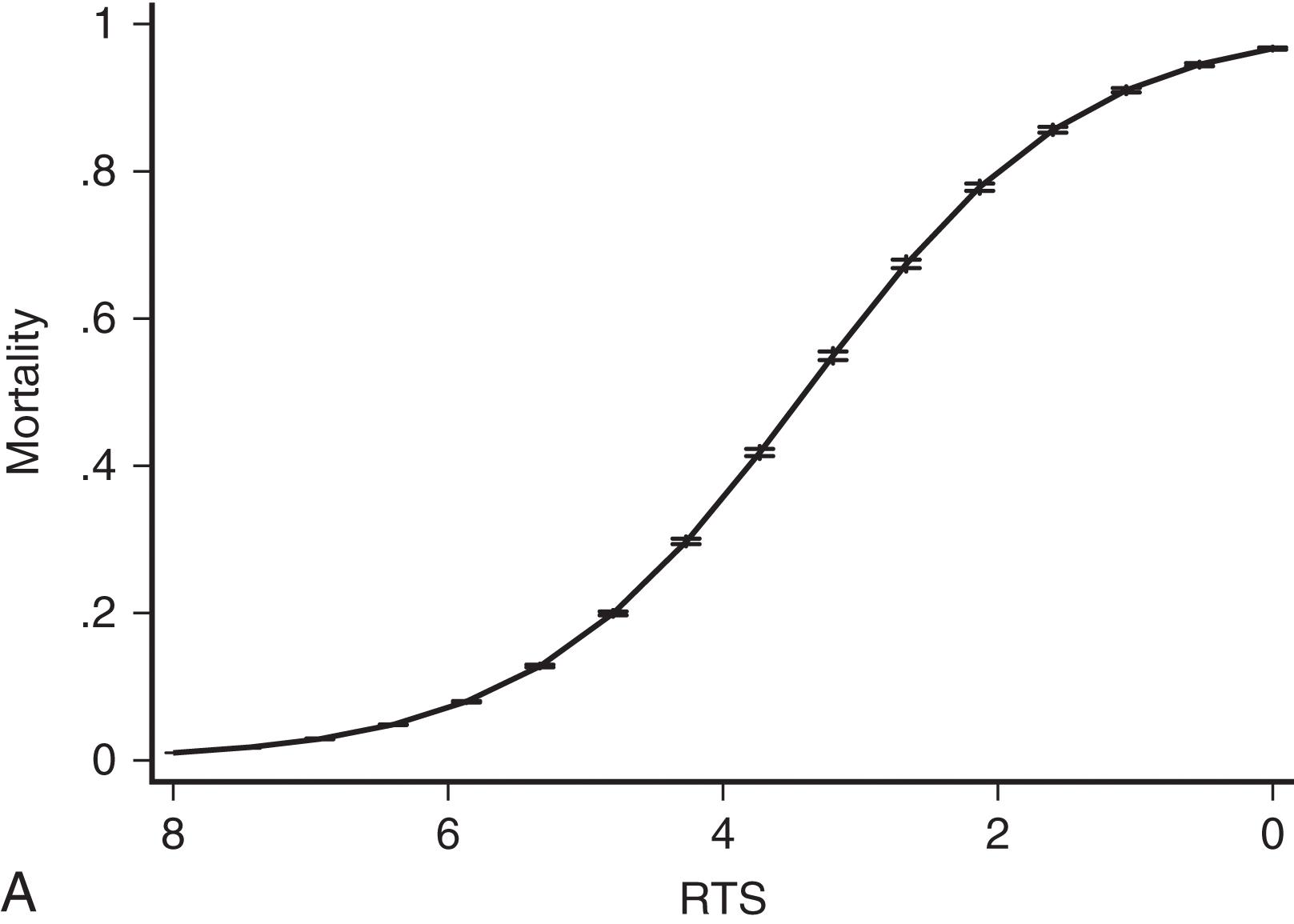
Currently, the most popular measure of overall physiologic derangement is the RTS. It has evolved over the past 30 years from the Trauma Index, through the Trauma Score to the RTS in common use today. The RTS is defined as a weighted sum of coded values for each of three physiologic measures: GCS, SBP, and respiratory rate. Coding categories for the raw values were selected on the basis of clinical convention and intuition. Weights for the coded values were calculated using a logistic regression model and the Multiple Trauma Outcome Study (MTOS) data set. The RTS can take on 125 possible values between 0 and 7.84:
where RR is respiratory rate.
Even though the RTS is in common use, it has many shortcomings. As a triage tool, the RTS adds nothing to the vital signs and brief neurologic examination because most clinicians can evaluate vital signs without mathematical “preprocessing.” As a statistical tool, the RTS is problematic because its additive structure simply maps the 125 possible combinations of subscores into a curious, nonmonotonic survival function ( Fig. 5 A). Finally, the reliance of RTS on the GCS score makes its calculation for intubated patients problematic. Despite these difficulties, the RTS discriminates survivors from nonsurvivors surprisingly well ( Fig. 5 B). Nevertheless, it is likely that a more rigorous mathematical approach to an overall measure of physiologic derangement would lead to an improved score.
A new trauma score (NTS) was developed by Jeong et al., based on revised parameters of RTS, including the adoption of the actual GCS score instead of a GCS code, the revision of the coded SBP intervals, and the use of coded peripheral oxygen saturation (SpO2) instead of respiratory rate.
Predictive performance of the NTS for in-hospital mortality in a sample of 3263 patients showed better discrimination and mortality prediction than the RTS, and our analysis of the 2017 NTDB concurs ( Table 3 and Fig. 6 ).
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here