Haemodynamics and Blood Flow

TYPES OF FLOW

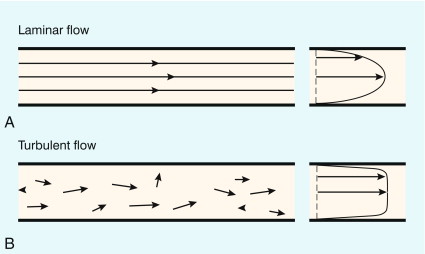
The two essential flow states are laminar and turbulent. At low velocity, fluid flow is laminar ( Fig. 2-1A ). This is characterised by the motion of fluid along well-defined paths called streamlines. At very high velocities, fluid flow is turbulent ( Fig. 2-1B ); particular elements of the fluid no longer travel along well-defined paths, and there is a random component to the motion of the fluid.

Concepts of laminar and turbulent flow first arose from consideration of flow in long straight tubes. It was found that a dimensionless number called the Reynolds number ( Re ) was useful in characterising the fluid flow. The Reynolds number is defined as:

where ρ is the fluid density, L is the vessel diameter, V is the mean velocity and μ is the fluid viscosity. For a wide variety of fluids the transition to turbulence takes place at a value of Re of about 2000. For flow in which Re is about 2000 the fluid flow will alternate between turbulent and laminar. When velocity is increased so that the Re is above the critical value, turbulence will take a small amount of time to develop. During pulsatile flow it is therefore possible for the flow to be laminar at values of Re higher than the critical value, because turbulence does not have time to develop before the blood velocity has decreased.

There is also a third flow state called disturbed flow, which refers to variations in velocity magnitude and direction which occur at low values of Re . The most important example of this is seen with the phenomenon of vortices, which are regions of circulating flow often produced when there is some obvious change in vessel geometry such as a stenosis, or the normal carotid bulb. The pattern of vortex production will change as the degree of stenosis and blood velocity increase. During steady flow at low Re values the vortex will be stable and limited to the region immediately behind the stenosis. At low velocity the fluid flow within the vortex is actually laminar. At higher Re values there will be vortex shedding at regular time intervals. Again this is not strictly turbulence, as the velocity magnitude and direction at any location is not random, but follows a regular pattern. At even higher Re values, the vortex shedding will be combined with the random flow patterns of true turbulence. Vortices which are shed travel a few diameters downstream and eventually die out as their energy is absorbed through viscous losses. During pulsatile flow, vortex shedding may occur for only a portion of the cardiac cycle.

The effect of the flow state on the Doppler waveform is illustrated in Figure 2-2 . Doppler spectra are shown from the normal femoral artery in Figure 2-2A ; in this case flow is laminar. Within the sample volume the blood velocity magnitude and direction are similar for all of the red cells, hence the spectral width is low and the waveform outline is smooth. In the post-stenotic region of a diseased artery the Doppler waveform is more complex ( Fig. 2-2B ). The blood which was at rest in the poststenotic region during diastole is accelerated through the sample volume. For this blood, flow is laminar and the initial up-slope of the waveform has a smooth outline with low spectral width, whereas blood which was in the prestenotic region during diastole has to pass through the stenosis, producing disturbed and turbulent flow within the sample volume. The variation in velocity magnitude and direction which this produces results in an increase in the spectral width ( Fig. 2-2B ), and the waveform outline is no longer smooth.

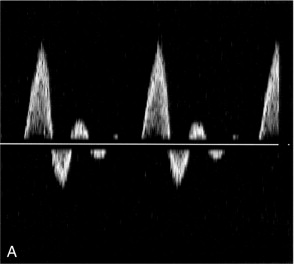
In the normal circulation, flow is mostly laminar; however, disturbed flow may occur in particular vessels such as the carotid arteries. Flow recirculation is commonly seen in the region of the bulb and there may be disturbed flow in the distal region. For the purposes of clinical Doppler ultrasound, very little practical distinction is made between disturbed and turbulent flow. The presence of spectral broadening is often indicative of pathological change in the vessel.

A summary of points concerning flow state is given in Box 2.1 .

PRESSURE AND ENERGY

In the circulation the essential principle is that a pressure gradient must be created in order for blood to flow; this is produced by the contraction of the heart and the resultant ejection of blood into the aorta and systemic vessels.

Energy is a useful concept in fluid mechanics. When there is steady flow of an incompressible frictionless fluid, the principles of conservation of energy can be used to give Bernoulli’s equation.

This is a simple expression which dem+onstrates that there will be an interchange between the different types of energy within the circulation. In the human body, however, the flow is not steady and the above equation must be modified slightly to account for the energy required to accelerate the fluid. Energy is conserved in this simple ideal lossless system. In the circulation, energy is lost in the form of heat through viscous effects, manifested through friction of the blood at the vessel wall and between adjacent layers of blood. Energy losses are highest in the region of a stenosis, as there is considerable friction during turbulent flow and vortex motion.

Within a stenosis there will be an increase in blood kinetic energy associated with increase in blood velocity, and according to Bernoulli’s equation there is a corresponding fall in blood pressure. If there was no energy loss within the system then the decrease in velocity (and hence kinetic energy) in the poststenotic region would be compensated by a return of the pressure to the prestenotic level. In practice the loss of energy through turbulence and vortex shedding gives rise to a pressure drop across the stenosis whose magnitude is dependent on the degree of stenosis.

The most common application of Bernoulli’s equation is in the prediction of pressure drop across a stenosed cardiac valve. The equation may be simplified to:

where V is the measured velocity in m/s, and P is the pressure drop in mmHg. Points concerning pressure and energy are summarised in Box 2.2 .

VELOCITY PROFILES

The Doppler ultrasound spectrum is critically related to the detailed variation of velocity within the vessel of interest. The velocity of the blood will vary as a function of its position within the vessel; this is called the velocity profile. The most commonly mentioned velocity profile is the parabolic velocity profile.

Strictly speaking, a parabolic velocity profile only applies to steady laminar flow in a long straight tube, when there is maximum velocity in the centre of the vessel and zero velocity at the edge of the vessel ( Fig. 2-1A ). The profile is radially symmetric, which means that it is the same regardless of which diameter is considered. The shape of the profile is an exact mathematical equation, that of a parabola.

Velocity profiles in vessels in the body are generally more complex; they may not be even approximately radially symmetric and they vary with time during the cardiac cycle. It is worth exploring the various effects that will influence true velocity profiles in the circulation.

Entrance Effect

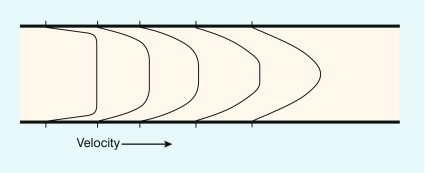
The velocity profile in a vessel is strongly influenced by the distance of the region of interest from the entrance to the vessel. For a long straight vessel, when there is steady flow, the profile is initially flat at the entrance to the vessel. With increasing distance from the entrance the profile will change, becoming parabolic at a distance called the inlet length ( Fig. 2-3 ).