Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Evaluation Of Renal Function, Water, Electrolytes, And Acid-Base Balance
Introduction
Laboratory tests for evaluation of disorders of renal, water, electrolyte, and acid-base status are the most common procedures performed in clinical chemistry laboratories. Screening tests in most laboratories are often grouped together in a basic metabolic panel because acid-base and electrolyte disorders are seen in a high percentage of hospitalized individuals, and electrolyte disorders are frequent complications of treatment for a variety of common conditions. Furthermore, renal disease is one of the major sequelae of common disorders such as diabetes and hypertension. Hence, proper interpretation of laboratory tests of renal, electrolyte, and acid-base disorders requires an understanding of pathophysiology of these systems. Most central to the understanding of these disorders is knowledge of renal function and how the kidneys regulate extracellular volume and tonicity.
Volumes And Osmolality Of Body Fluid
The body fluid is an aqueous solution containing electrolytes and nonelectrolytes, consisting of intracellular and extracellular compartments. The intracellular compartment is not a single compartment; rather, each cell has its own separate environment, communicating with other cells only through interstitial fluid and plasma. Consequently, differences exist among cells in various tissues in their solute composition and concentrations. However, because cell membranes are permeable to water through the ubiquitous presence of aquaporins (water channels), osmotic equilibrium is maintained so that the osmolality of all cells is the same as that of extracellular fluid ( ).
Before the discovery of aquaporins, it was believed, erroneously, that all cell membranes are readily permeable to water. We now know that cell membranes are virtually impermeable to all substances, large and small. Even a molecule as small as water, with the molecular mass of a mere 18 Da, needs aquaporins in order to cross the cell membrane. Even after the discovery of aquaporins, it was widely believed that small gaseous substances such as carbon dioxide (CO 2 ) can readily diffuse across cell membranes. It has been shown subsequently that CO 2 cannot diffuse across cell membranes easily in some cells in the absence of aquaporins. For example, the apical membrane of the gastric mucosa is impermeable to CO 2 because of the absence of aquaporins, whereas the basolateral membrane of the same cell allows ready diffusion of CO 2 owing to the presence of aquaporin ( ). The same appears true of the colonic mucosa ( ; ).
Operation of normal metabolic functions of the body requires maintenance of an optimal ionic strength of its environment, primarily the intracellular fluid, where most metabolic activities occur. The main functions of homeostatic mechanisms of the body are to provide such an environment. Because the extracellular fluid is not the site of major metabolic activity, substantial alteration in its ionic strength may occur without adverse effects on body function. The main function of the extracellular fluid is to serve as a conduit among cells and among organs. The plasma is a route of rapid transit, and the interstitial fluid serves as a slow supply zone. The ability of extracellular fluid to function efficiently as a conduit requires maintenance of optimal volume, particularly of vascular volume. An additional important function of the extracellular fluid is regulation of the intracellular volume and its ionic strength. Because osmotic equilibrium exists between cells and the extracellular fluid, any alteration in extracellular osmolality is followed by an identical change in intracellular osmolality, which is accompanied by a reciprocal change in cell volume through transcellular water movement ( ).
Although cells and organs can be supplied with substrate and relieved of metabolic products with a much slower rate of circulation, normal cardiac output is required to supply sufficient amounts of oxygen for the body’s metabolic needs. Normal plasma volume is a prerequisite for maintenance of normal circulation. Because plasma is in equilibrium with the interstitial fluid, the maintenance of normal vascular volume requires normal extracellular volume. Low extracellular volume results in impaired organ perfusion, which manifests most promptly as insufficient oxygen delivery. Excessive extracellular volume leads to increased blood volume, eventually leading to pulmonary edema.
Transfer of fluid between the vascular space and the interstitial space is regulated by the Starling forces. The ultimate purpose of maintaining adequate intravascular volume is to maintain adequate hydrostatic pressure, which is necessary for diffusion of fluid from the vascular space into the interstitial space. Movement of fluid, nutrients, and electrolytes occurs in systemic capillaries through the vascular endothelial fenestrae. On the other hand, movement of solutes and water across the capillaries of the brain is entirely transcellular through endothelial cells because the intercellular gap (endothelial fenestrae) of the brain capillary endothelium is tightly closed. This is termed the blood-brain barrier ( ). In order to supply nutrients and oxygen to the brain, perfusion is what matters, not perfusion pressure. The position of the brain in relation to the heart is such that when blood pressure is too low, perfusion of the brain will cease before that of other organs ( ).
Measurement Of Body Fluid Volumes
Total body water can be determined by dilution of various substances, including deuterium, tritium, and antipyrine. The gold standard of the measurement is using either tritiated water or deuterium oxide. The former is a radioactive isotope, and the latter requires a complicated method for its measurement. Both are very expensive. Furthermore, deuterium hydrogen is also known to equilibrate with H atoms besides those found in water molecules; as a result, total body water obtained with D 2 O was shown to be slightly higher ( ; ). Another nonradioisotope used for the measurement of total body water is H 2 O with 18 O isotope, which, unlike D 2 O, does not equilibrate with O atoms outside of H 2 O. Consequently, total body water measured with D 2 O is about 3% larger than that measured with H 2 18 O. As a cheap alternative, antipyrine has been introduced, which was used extensively in the 1940s and 1950s ( ). However, subsequent studies indicated that antipyrine is not a very reliable dilution marker. It is metabolized in the liver; therefore, the equilibrium concentration at time zero must be obtained by interpolating the results ( ).
More recently, the measurement of body fluid volumes by bioelectrical impedance analysis has become very popular. However, the results are not as accurate as the dilution methods and the technology is still evolving. The main advantages of this method are easy applicability, noninvasiveness, and portability of measurements. The portability allows measurements of body fluid volumes in outpatient clinics and at the bedside. The method is based on the principle that the body is an electrical conductor with a certain amount of resistance to flow (impedance), and resistance (R) is proportional to its length (L) and inversely proportional to the cross-sectional area (A). Hence, R (resistance) = ρL/A, where ρ is the resistivity of the conducting material, that is, the body. Since V = AL, V = ρL2/R. The body fluid offers two types of resistance to an electrical flow: resistive resistance and capacitative resistance. The former is simply called resistance , whereas the latter is called reactance . Impedance of the body to an electrical flow is the combination of these two types of resistance. The cell membrane, which is made of lipid, acts like capacitance, and is the cause of capacitative resistance. At zero or low frequency, electrical current does not penetrate the cell membrane and, therefore, flows only through the extracellular fluid. At a very high frequency, electrical current flows through both extracellular and intracellular fluid compartments ( ; ).
The term bioelectrical impedance analysis is used when single or multiple frequencies of up to 8 frequencies are used, whereas the term bioelectrical spectroscopy is used when 256 or more multiple frequencies are used. Bioelectrical impedance analysis has been used to measure fat-free mass, extracellular fluid volume and intracellular fluid volume, and total body water. In bioelectrical spectroscopy, mathematical modeling and mixture equations are used to generate the relationship between R and body fluid volumes.
A mathematical model widely used is called the Xitron equation , which has been further modified. Another model, called the body composition spectroscopy equation , using different assumptions, has been developed subsequently. Comparison of the two methods in dialysis patients whose change in total body water can be determined from the ultrafiltration volume during dialysis, indicated that the latter method was more accurate ( ).
Body Fluid Volumes
Total body water measured with antipyrine in hospitalized adults without fluid and electrolyte disorders is about 54% of body weight. The fractional water content is higher in infants and children and decreases progressively with aging. The water content also depends on the body content of fat; women and obese persons, because of their higher fat content, have less water for a given weight. A useful shortcut for the calculation of total body water, using the fact that 54% of body weight in kg is body water and 1 kg is 2.2 lb, is:
For an obese subject, subtract 10% from the calculated body water; for a lean person, add 10%. For a very obese person, subtract 20%. Women have about 10% less body water than men for the same body weight ( ).
Extracellular volume is measured directly; intracellular volume is estimated as the difference between total body water and extracellular volume. The measurement of total body water is reliable, but the measurement of extracellular volume is not. Although many different markers have been used to measure extracellular volume, no ideal marker has been found. Markers that have been used to measure extracellular volume include sodium, chloride, bromide, mannitol, inulin, sucrose, sulfate, thiosulfate, and thiocyanate. Markers such as sodium, chloride, and bromide are not located exclusively in the extracellular compartment; rather, they penetrate the cells to varying extents. Other markers, such as mannitol, inulin, sucrose, sulfate, thiosulfate, and thiocyanate, do not penetrate certain parts of the extracellular fluid. Extracellular volume has also been estimated indirectly by the degree of dilution of serum Na following administration of mannitol on the principal that mannitol in the extracellular fluid would cause osmotic withdrawal of water from the cell. Thus, depending on the type of marker used, extracellular fluid volume could vary from 27% to 53% of total body water. Extracellular volume has also been estimated by a formula using body weight and height ( ).
Extracellular volume measured with chloride and expressed as percent of total body water varies from 42% to 53%, greater in older subjects and women. Extracellular volume measured with inulin or sulfate is smaller, about 30% to 33% of total body water. For discussion in this chapter, a value of 40% of total body water will be considered to represent extracellular volume. Extracellular volume is further divided into 3 fractions: interstitial (space between cells) volume (28% of total body water), plasma volume (8%), and transcellular water volume (4%; Box 15.1 ). Transcellular water includes luminal fluid of the gastrointestinal tract, the fluids of the central nervous system, and fluid in the eye as well as the lubricating fluids at the serous surface.
BOX 15.1
Volumes of Body Fluid Compartments ∗
∗ A normal man weighing 73 kg (160 lbs) with 40 L of total body water is used as a model.
ΔHCO 3 − and ΔpCO 2 represent the difference between normal and actual values in bicarbonate and pCO 2 , respectively.
Composition Of The Body Fluid
Extracellular Composition
The concentrations of electrolytes in plasma are easily measured and their values well known. These concentrations increase by about 7% when expressed in plasma water, because about 7% of plasma is solids. Thus, plasma sodium is 140 mEq/L but the concentration in plasma water is about 150 mEq/L. The concentrations of electrolytes in interstitial fluid are different from those in plasma because of the difference in protein concentrations between plasma and interstitial fluid. The differences in electrolyte concentrations between plasma and interstitial fluid can be predicted by the Donnan equilibrium ( Table 15.1 ). With normal plasma protein concentrations, the concentrations of diffusible cations are higher in plasma water than in interstitial water by about 4%, while the concentrations of diffusible anions are lower in plasma than in interstitial fluid by about 4%. The concentrations of calcium and magnesium in the interstitial fluid are lower than the values predicted by the Donnan equilibrium, because they are substantially protein bound (Elkin et al., 2010).
TABLE 15.1
Electrolyte Concentrations in Extracellular and Intracellular Fluids
| Plasma | Interstitial Fluid | Plasma Water | Cell Water (Muscle) | |||||
|---|---|---|---|---|---|---|---|---|
| (mEq/L) | (mmol/L) | (mEq/L) | (mmol/L) | (mEq/L) | (mmol/L) | (mEq/L) | (mmol/L) | |
| Na + | 140 | 140 | 145.3 | 145.3 | 149.8 | 149.8 | 13 | 13 |
| K + | 4.5 | 4.5 | 4.7 | 4.7 | 4.8 | 4.8 | 140 | 140 |
| Ca ++ | 5.0 | 2.5 | 2.8 | 1.4 | 5.3 | 5.3 | 10 -7 | 0.5 x 10 -7 |
| Mg ++ | 1.7 | 0.85 | 1.0 | 0.5 | 1.8 | 0.9 | 7.0 | 3.5 |
| Cl − | 104 | 104 | 114.7 | 114.7 | 111.4 | 111.4 | 3 | 3 |
| HCO 3 − | 24 | 24 | 26.5 | 26.5 | 25.7 | 25.7 | 10 | 10 |
| SO 4 = | 1.0 | 0.5 | 1.2 | 0.6 | 1.1 | 0.55 | – | – |
| P | 2.1 | 1.2 + | 2.1 ++ | 1.2 + | 2.2 | 1.25 + | 107 | 57 +++ |
| Protein | 15 | 1 | 8 | 0.5 | 16 | 1 | 40 | 2.5 ∗ |
| Organic anion | 5 | 5 | 5.6 | 5.6 | 5.3 | 5.3 | – | – |
+ The calculation is based on the assumption that the pH of the extracellular fluid is 7.4 and the pK of inorganic H 2 PO 4 − is 6.8.
++ The concentration of P in the interstitial fluid is higher than that of plasma by the Donnan effect but lower by lower protein-bound phosphate. These two opposing effects keep interstitial phosphate concentration about equal to that of plasma.
+++ The intracellular molal concentration of phosphate is calculated with the assumption that the pK of organic phosphates in the cell is 6.1 and the intracellular pH 7.0.
∗ The calculation is based on the assumption that each mmol of intracellular protein has, on average, 15 mEq.
The extracellular fluid space is not merely the site of passive passageway for the movement of nutrients and metabolites between plasma and cells and the exchange of oxygen and CO 2 . The extracellular space also contains extracellular matrix, which provides structural integrity and support for the surrounding cells but also participates in signaling transduction to the cells. The main molecules contained in the extracellular space are many different types of fibrous proteins, such as collagen, elastin, laminin, and fibronectin, and glycoproteins and hyaluronic acid ( ). Glycoproteins consist of sulfated glycosaminoglycan attached covalently to protein; examples include heparan sulfate, dermatan sulfate, and chondroitin sulfate. Hyaluronic acid is one form of glycosaminoglycan, which is neither sulfated nor attached to protein, and is the most abundant glycosaminoglycan in the extracellular space. Both hyaluronic acid and sulfated glycoproteins are highly anionic and surrounded by many water molecules in a gel-like state. This space excludes distribution of proteins. In the other part, proteins diffuse freely and communicate with lymphatics. Interspersed within the interstitial space is elastin, which provides the elastic property of the interstitial tissue. This property is necessary for generation of a normal negative pressure of the interstitial space and a positive pressure with the development of edema ( ; ; ).
The fact that extracellular matrix proteins participate in cellular signaling is shown by the findings that many extracellular matrix proteins—such as collagen, laminin, fibronectin, and vitronectin—are ligands for the transmembrane receptor proteins, such as integrin. In fact, as another name for integrin is vitronectin receptor , many important physiologic effects of vitronectin are mediated through integrin ( ).
Intracellular Composition
While sodium, chloride, and bicarbonate are the main solutes in extracellular fluid, potassium, magnesium, phosphate, and proteins are the main solutes in the cell. The intracellular concentrations of sodium and chloride cannot be measured accurately and are estimated by subtracting the amount that is extracellular from the total tissue value. Since concentrations of electrolytes in the extracellular fluid are high, a small error in extracellular water volume measurement will cause a large error in the measurement of intracellular concentration of these ions. The concentration of bicarbonate is calculated from cell pH, and the bicarbonate concentration shown in Table 15.1 is based on the assumption that average cell pH is 7.0. It should be noted further that the intracellular fluid consists of many different subcompartments, such as mitochondria. In many cells, such as skeletal muscle and the liver, mitochondria represent a large fraction of the cell mass and the electrolyte composition of the mitochondria is often quite different from the cell cytoplasm. For example, the pH of mitochondrial matrix is about 7.8, which is 0.7 pH units higher than the pH of the cytoplasm. Since transport of phosphate through the inner mitochondrial membrane occurs as neutral phosphoric acid, the eventual total concentration of phosphate in the mitochondria is expected to be about 5 times higher than that in the cytoplasm ( ).
The electrolyte composition of intracellular fluid is not identical throughout the tissues. For example, the concentration of chloride in muscle is very low, about 3 to 4 mEq/L, but it is about 75 mEq/L in erythrocytes. A very low chloride concentration in skeletal muscle is attributed to the strongly negative resting membrane potential, about −90 mV. In contrast, the electrical potential of red blood cells is about −10 mV. Distribution of chloride across muscle estimated from the Nernst equation would predict the concentration of 3.5 mEq/L when the electrical potential is −90 mV in the muscle cell and 72 mEq/L when the potential is −10 mV in the red blood cell. Slightly higher values can be explained by secondarily active transporters, such as sodium-potassium-chloride transporters (NKCC). The concentration of potassium in the muscle cell is about 140 mEq/L, but in the platelets only about 118 mEq/L, and the lower potassium concentration is also explained by lower membrane potential, about −70 mV.
The concentration of sodium in the cell cannot be predicted by the membrane potential since the values are far from the equilibrium predicted by the Nernst equation. If it were the electrochemical equilibrium, the intracellular concentration of sodium would be much greater than that of the extracellular fluid. The much lower concentration of sodium in the cell of the latter than predicted from the equation can be explained by Na + -K + -ATPase that pumps sodium out of the cell constantly. The concentration of sodium in the muscle and red blood cell is about 13 mEq/L, but in the leukocytes about 34 mEq/L. The main phosphate in the red blood cell is 2,3 DPG, but in the muscle ATP and creatinine phosphate are the main phosphates. Because the muscle represents the bulk of the body cell mass, it is customary to use the electrolyte concentration of the muscle cells as representative of the intracellular electrolyte concentration. A substantial part of the anions inside the cell are polyvalent ions, such as phosphate and protein; consequently, the total ionic concentration in the cell in mEq/L is higher than that of the extracellular fluid in order to maintain osmotic equilibrium with the extracellular fluid ( ).
Even then, the total solute concentration of electrolytes in the cell is less than the total solute concentration of electrolytes in the extracellular fluid. The difference is explained by the accumulation of organic solutes in the cell at concentrations that are much higher than those in the extracellular fluids. These organic solutes include sorbitol, myoinositol, taurine, betaine, and glycerophosphocholine. These solutes are not only the constituents of normal solutes in the cell but also participants in the regulation of cell volumes in the presence of changes in extracellular tonicity. For example, in the presence of hypertonicity, the intracellular concentrations of these solutes increase either by increased synthesis or by increased cellular uptake. The concentration of sorbitol in the cell with hypertonicity increases by the increased production by activating the enzyme aldose reductase while reducing its metabolism to fructose. Similarly, the concentration of glycerophosphocholine increases by the increased activity of the main synthetic enzyme, NTE (neuropathy target esterase). On the other hand, the increased cellular concentration of betaine, myoinositol, and taurine are achieved by the increased number of transporters—namely, BGT1 (betaine-GABA transporter), SMIT (sodium myoinositol transporter), and TauT (taurine transporter). Regulation of production of these various chemicals is orchestrated by the TonEBP transcription factor described earlier (Lee et al., 2011).
Measurement Of Plasma Osmolality
Osmolarity refers to the number of moles of solute in a liter of solution, whereas osmolality refers to the number of moles of solute in a kilogram of water (solvent). Osmolality is the preferred term, since measurements of both osmolarity and osmolality are based on colligative properties, which are based on the number of particles dissolved in a given number of water molecules. Examples of colligative properties, which depend on the number of solute particles, include freezing point depression, boiling point elevation, and vapor pressure lowering. The molecular mass of water represents the number of water molecules more accurately than the volume, because water volume changes with temperature and the molecular mass does not. One should note, however, that 1 kg of water occupies exactly 1 L at 4° C. However, the terms osmolality and osmolarity are often used interchangeably because changes in volume of liquid water with temperature are negligible ( ).
One mole of NaCl in solution contains 2 osmoles because NaCl is dissociated to Na + and Cl − . One mole of D-glucose in solution contains 1 osmole since glucose does not dissociate. One mole of Na 3 PO 4 in solution contains 4 osmoles, since it will dissociate into 3 Na + ions and one PO 4 = ion. To calculate the osmolality of a solution whose solute dissociates into more than one particle, the following equation is used:
where M is molarity and a is the number of particles into which a molecule of the substance dissociates.
When the osmolal concentration of the extracellular fluid increases by accumulation of solutes that are restricted to the extracellular fluid (effective osmols)—for example, glucose, mannitol, and sodium—osmotic equilibrium is reestablished as water shifts from the cell to the extracellular fluid (ECF), increasing intracellular osmolality to the same level as the extracellular osmolality. When the extracellular osmolality increases by accumulation of solutes that can enter the cell freely (ineffective osmols)—for example, urea and alcohol—the osmotic equilibrium is achieved by entry of those solutes into the cell. Since most of the solutes normally present in the extracellular fluid are effective osmols, loss of extracellular water (e.g., insensible losses) will increase effective osmolality and, hence, cause shift of water from the cells. Reduction in extracellular osmolality either by loss of normal extracellular solutes or by retention of water reduces effective osmolality for the same reasons, causing a shift of water into the cells.
Osmolality of serum or plasma can be measured directly with an osmometer as described in Chapter 4 on the principles of instrumentation or estimated as the sum of the concentration of all the solutes in the plasma. Because an osmometer does not distinguish between effective and ineffective osmols, effective osmolality can only be estimated. As it happens, urea is the only ineffective osmol that is present in substantial concentrations in the normal plasma, 5 mOsm/L. In the normal plasma, therefore, total osmolality is nearly equal to effective osmolality. Plasma osmolality is estimated as follows:
In the use of this formula, osmolality of sodium and accompanying anions are overestimated by not considering the osmotic coefficient and assuming that all serum anions are univalent. On the other hand, osmolality is underestimated by ignoring nonsodium cations and their accompanying anions. At normal serum glucose and urea concentrations, osmolality almost equals serum Na + × 2 because the opposing errors cancel each other. It should be noted that for the contribution of urea and glucose for serum osmolality, their values in mg/dL is divided by one-tenth of each (2.8 and 18) of their molecular weights (28 and 180) because osmolality is expressed as mOsm/L, not mOsm/dL ( ).
Many of the solutes that may accumulate in the body in certain abnormal states are anions of an acid, for example, salicylate, glycolate, formate, lactate, and beta-hydroxybutyrate. These substances should not be added in estimating plasma osmolality since they are largely balanced by sodium and, therefore, already accounted for when plasma sodium is multiplied by 2. Nonelectrolyte solutes that accumulate abnormally in the serum—for example, ethanol, ethylene glycol, methanol, and mannitol—will cause the measured osmolality to exceed the calculated osmolality, producing an osmolal gap. This osmolal gap is a useful clinical clue to the presence of the toxic substances listed earlier. Accumulation of neutral and cationic amino acids also causes a serum osmolal gap ( ).
Effect of Hyperglycemia on Serum Na +
The permeability of a membrane for a given solute varies with the cell type. For example, glucose does not accumulate in muscle. It does not enter the muscle cell freely and, after entering the cell with the help of insulin, it is quickly metabolized. Thus, glucose is an effective osmol for the muscle cell—for example, hyperglycemia will cause a shift of water from the muscle cell. On the other hand, glucose is an ineffective osmol for red blood cells, liver, kidney cells, and most brain cells because it enters these cells freely. Glucose is generally categorized as an effective osmol mainly because muscle cells represent the largest body cell mass, as noted previously in this chapter. Accumulation of glucose or mannitol in the extracellular fluid is a well-known cause of hyponatremia because, as discussed in Chapter 9 , glucose is osmotically active and induces diffusion of water from the cells to the extracellular fluid, diluting its electrolytes. The fluid shift affects concentrations of all extracellular electrolytes, but its absolute effect is greatest on serum sodium because of its highest concentration. The relationship between change in serum sodium and change in glucose concentration in a normal adult is about 1.6 mEq/L of Na + for 100 mg/dL of glucose. However, the correction factor is not linear. When hyperglycemia is more severe, the change in serum sodium for a given change in glucose tends to be less, approaching 1.4 at serum glucose concentration of 1000 mg/dL. In sharp contrast, , on the basis of experiments on normal subjects, concluded that the correction factor was much larger, a 2.4 mEq/L change in serum sodium for every 100 mg/dL change in glucose. A problem with this experiment and the conclusion was that the authors disregarded the effect of water contained in intravenous glucose and urine output on serum sodium ( ). Furthermore, infusion of somatostatin during induction of hyperglycemia would have increased serum potassium, and infusion of insulin during treatment of hyperglycemia would have had an opposite effect on serum potassium concentration. Changes in serum potassium have the opposite effects on serum sodium concentration ( ; ).
These figures suggested by various formulas are valid, however, only when the volume of distribution of glucose is between 40% and 50% of total body water. Volume of distribution of glucose refers to a theoretical volume into which glucose would be evenly distributed when none of the administered glucose is excreted and none metabolized. For example, if 10 g (10,000 mg) of glucose is given to a person, and the serum concentration were to increase by 1000 mg/L (100 mg/dL, with the assumption that none was metabolized and none excreted), the volume of distribution would be 10 L. Normally, the volume of distribution of glucose is slightly greater than the extracellular volume because some cells allow free diffusion of glucose. As the volume of distribution of glucose in relation to total body water is increased, the effect of glucose on serum sodium decreases. Decreased volume of distribution of glucose has an opposite effect. The change in serum Na caused by hyperglycemia can be estimated with the following formula:
where ΔNa is a reduction in serum Na + in mEq/L for each 100 mg/dL increase in glucose, and a the fraction of the volume of glucose distribution over total body water ( ).
In conditions with marked expansion of extracellular volume—for example, congestive heart failure and other edema-forming states—the volume of distribution of glucose represents a much greater fraction of total body water and, hence, a fall in serum sodium caused by hyperglycemia would be much less than usual. For example, when the volume of distribution of glucose is 80% of total body water (0.8), the decrease in serum Na + for 100 mg/dL rise in glucose would be only 0.56 mEq/L; (5.6 − 5.6 × 0.8)/2 = 0.56. When the volume of distribution of glucose is 20% of total body water, ΔNa + would be 2.2 mEq/L for a 100 mg/dL increase in glucose ( ).
Tonicity
The concept of tonicity of a solution is based on the effect of a particular solution on the volume of cells. A hypertonic solution is one that shrinks the cells, while a hypotonic solution is one that causes swelling of the cells. An isotonic solution is one that does not induce any volume change in the cells. A solution of 0.9% saline (154 mM solution of sodium chloride) is isotonic in relation to the normal body fluid. When the term tonicity is applied to a fluid in vitro, as in the urine, it is used almost interchangeably with total osmolality since voided urine is no longer in contact with cells. Thus, urine with a high concentration of urea is called hypertonic ( ; ).
Osmolality and Specific Gravity
The specific gravity of a solution is the mass of the solution divided by the volume of the solution. Whereas osmolality of fluid depends on the osmolal concentration of its solute, specific gravity is determined by the weight of the solute relative to the volume that it displaces in solution. Plasma protein contributes little to osmolality because of its low molal concentration despite its great weight but is the major factor determining specific gravity of plasma. Urinary specific gravity and osmolality usually change in parallel, but discrepancy occurs between the two with heavy proteinuria and severe glycosuria. Sometimes, specific gravity is confused with the molecular mass, and specific gravity is thought to correlate with the molecular mass. This may lead to the erroneous conclusion that the larger the molecular mass, the greater the specific gravity. Such correlations do not exist. Glucose, for example, has a molecular mass of 180 Da, but has a greater effect on urine specific gravity than albumin, which has nearly 40 times the molecular mass of glucose. Triglyceride has a molecular mass of about 850 Da, but urine specific gravity is less than 1 ( ; ; ).
The main determinant of specific gravity of plasma is protein, much more than NaCl and glucose, not because it has a greater effect than the latter but because the normal protein concentration at 70 g/L dominates over all other solutes. The normal plasma concentration of NaCl is merely 9 g/L and that of glucose only 1 g/L. Consequently, iso-osmotic plasma has a specific gravity of 1.020 to 1.030, whereas iso-osmotic urine has a specific gravity of about 1.010.
Regulation Of Extracellular Volume
As discussed later, extracellular volume depends primarily on its sodium concentration, which is closely regulated by two hormones: antidiuretic hormone (ADH), which promotes water retention, and aldosterone, which promotes sodium retention, which, in turn, causes water to be retained with it, as discussed in Chapter 9 . Because the extracellular sodium concentration is maintained within a narrow range through the regulation of ADH release, the extracellular volume depends primarily on its sodium content. In most clinical situations, extracellular volume correlates well with vascular volume, which, in turn, usually correlates positively with the effective vascular volume. Effective vascular volume is an imaginary volume that reflects cardiac output in relation to the tissue’s demand for oxygen. Sometimes, effective vascular volume does not correlate well with vascular volume or extracellular volume ( ; ).
Effective vascular volume, rather than extracellular volume or vascular volume, is the chief determinant of how much extracellular fluid is retained. The location and type of sensors that perceive changes in effective vascular volume is not well known. Most physiologists consider the baroreceptors—located in the carotid sinus, the atria of the heart, and the aortic arch—likely candidates that send neural signals to the central nervous system, resulting in increases or decreases of ADH and altered sympathetic tone. However, the preponderance of evidence argues against effectiveness of such receptors in chronic states of altered effective vascular volume. For example, in a hypertensive patient with congestive heart failure, both atrial low pressure and arterial high pressure baroreceptors would sense a higher than normal pressure. Yet, the neurohumoral responses (e.g., high ADH, high catecholamines, and high renin and angiotensin concentrations) in such states suggest that the body somehow senses low effective vascular volume. In such conditions, the kidney responds appropriately by reducing urinary excretion of sodium and chloride. These physiologic responses to low effective vascular volume sometimes lead to a pathologic retention of salt. For example, salt is retained in congestive heart failure despite markedly expanded extracellular volume and vascular volume because effective vascular volume is decreased ( ).
Theoretically, there are two ways to alter the salt content of the body: to alter the intake of salt or to alter renal salt output. There is no well-developed mechanism that influences salt intake in response to changes in effective vascular volume. Thus, alterations in salt content of the body are achieved primarily through changes in renal salt output. Changes in renal salt output can be achieved through physical and humoral factors. The physical factors for renal salt regulation work through changes in the glomerular filtration rate (GFR) and in peritubular capillary oncotic and hydrostatic pressures. When other factors that influence renal salt output are kept unchanged, the greater the GFR, the greater the amount of sodium filtered and the greater the amount of sodium excreted. In general, however, tubular reabsorption rather than glomerular filtration plays the major role in the regulation of renal excretion of sodium. In advanced renal failure, the GFR may be 10% of normal, but patients with renal failure excrete the usual amount of sodium intake as people with normal renal function ( ).
Tubular reabsorption of sodium is regulated by humoral factors and physical factors. The latter’s influence on sodium reabsorption is limited mainly to the proximal tubule, where much of sodium reabsorption occurs passively through the paracellular (between cells ) pathway. Increased hydrostatic pressure on the peritubular capillary retards passive fluid reabsorption through the paracellular pathway while it promotes passive back diffusion of fluid into the tubular lumen. Increased oncotic pressure has the opposite effects. For example, in congestive heart failure, peritubular hydrostatic pressure is reduced because of the increased renal vascular resistance caused by constriction of both afferent and efferent arterioles. Constriction of afferent arterioles would also tend to reduce glomerular capillary hydrostatic pressure. However, the glomerular pressure does not decrease much because the constriction of efferent arterioles is even greater than that of afferent arterioles. The maintenance of glomerular filtration pressure helps to minimize a fall in GFR in volume depletion states. The result is an increase in filtration fraction (the ratio of GFR to renal plasma flow), which increases the concentration of plasma protein in the blood, leaving the glomerular capillary through the efferent arterioles to a greater extent than usual. Because the blood in the efferent arterioles flows into the peritubular capillaries, the oncotic pressure of the peritubular capillary would be higher than usual. A lower than usual hydrostatic pressure and a higher than usual oncotic pressure of peritubular capillary blood in volume depletion states tend to favor reabsorption of salt and water through the paracellular pathway of the proximal tubule, the tubular segment in which passive reabsorption of salt through the paracellular pathway plays a big role in overall renal tubular salt transport. Normally, the oncotic pressure of peritubular capillary plasma in the proximal tubule is about 25% higher than the peripheral blood plasma because the filtration fraction is 0.2. In states of volume depletion with a filtration fraction of 25%, the value would be 33% higher than that of the peripheral plasma. This anomalous behavior of changes in plasma protein concentration following glomerular filtration of plasma can be explained by the fact that the filtered volume of plasma must be expressed as a fraction of the remaining plasma volume. For example, when 120 mL of plasma is filtered with renal plasma flow of 600 mL, the filtered volume (120 mL) now represents 25% of the remaining plasma volume (480 mL). The protein concentration of the remaining plasma will increase accordingly ( ; ).
Humoral factors that influence tubular reabsorption of sodium include angiotensin II, aldosterone, atrial natriuretic peptide family of hormones, and catecholamines. Angiotensin II directly increases proximal tubular sodium reabsorption through its effect on the sodium-hydrogen exchanger-3 (NHE-3), and also indirectly by increasing aldosterone secretion, which in turn increases sodium reabsorption in the cortical collecting duct. Catecholamines influence sodium reabsorption mainly through their effects on renal blood flow, but may have some direct tubular effect in the proximal nephron.
Different types of atrial natriuretic peptide hormones exist. The most widely known are ANP, BNP, CNP, and urodilatin. ANP is produced mainly by the atrium of the heart; BNP, despite its original name, brain natriuretic peptide, is produced mainly by ventricles. Although BNP is now used widely as a marker of heart failure as its levels increase with dilatation of the ventricles (see Chapter 20 ), its physiologic relevance as the regulator of renal sodium excretion is doubtful. Despite a marked increase in ANP and BNP in congestive heart failure, there is markedly increased sodium reabsorption by the kidney in patients with congestive heart failure. The most important natriuretic peptide hormone for the renal excretion of sodium appears to be urodilatin. ( ; ; ).
The role of ADH in the regulation of extracellular volume is modest because of the overwhelming importance of osmolality as the main regulator of ADH secretion. For this reason, salt content of the body is the main determinant of the extracellular volume . When sodium is retained, a proportionate amount of water is retained in order to maintain normal serum osmolality. ADH secretion will occur despite hyponatremia only when the effective vascular volume depletion is very great ( ).
In the presence of primary water retention, as in the syndrome of inappropriate ADH secretion, extracellular volume could theoretically increase in the absence of sodium retention. However, massive water retention without sodium retention will cause only a modest increase in extracellular volume. For example, if a person with 40 L of total body water gains 10 L of water without a change in sodium content, serum sodium would decrease from 140 mEq/L to 112 mEq/L (140 × 40/50 = 112), a value that would cause severe morbidity or even death. This would increase the extracellular volume by only 4 L since the bulk (60%) of retained water would enter the cell. On the other hand, the same fluid volume retained with salt would remain almost exclusively in the extracellular space. In other words, the amount of water that can be retained without salt is limited by severe and fatal hyponatremia. This is the reason why a massive increase in extracellular volume, as in severe congestive heart failure, is possible only with massive sodium retention ( ).
The ultimate source of energy for reabsorption of sodium at various nephron segments is Na + -K + -ATPase located on the basolateral membrane, which transports 3 Na + out of the cell in exchange for 2 K + transported into the cell. The resulting reduction in intracellular sodium concentration and the negative cellular electrical potential allow passive diffusion of Na + into the cell through the luminal membrane. Four major sites of sodium reabsorption in the nephron utilize 4 different mechanisms of luminal sodium entry ( Fig. 15.1 ). Among humoral factors that have been proven or suggested as participating in the regulation of renal salt output, those with well-proven physiologic effects are aldosterone, catecholamines, angiotensin II, and perhaps ADH and prostaglandins ( ).
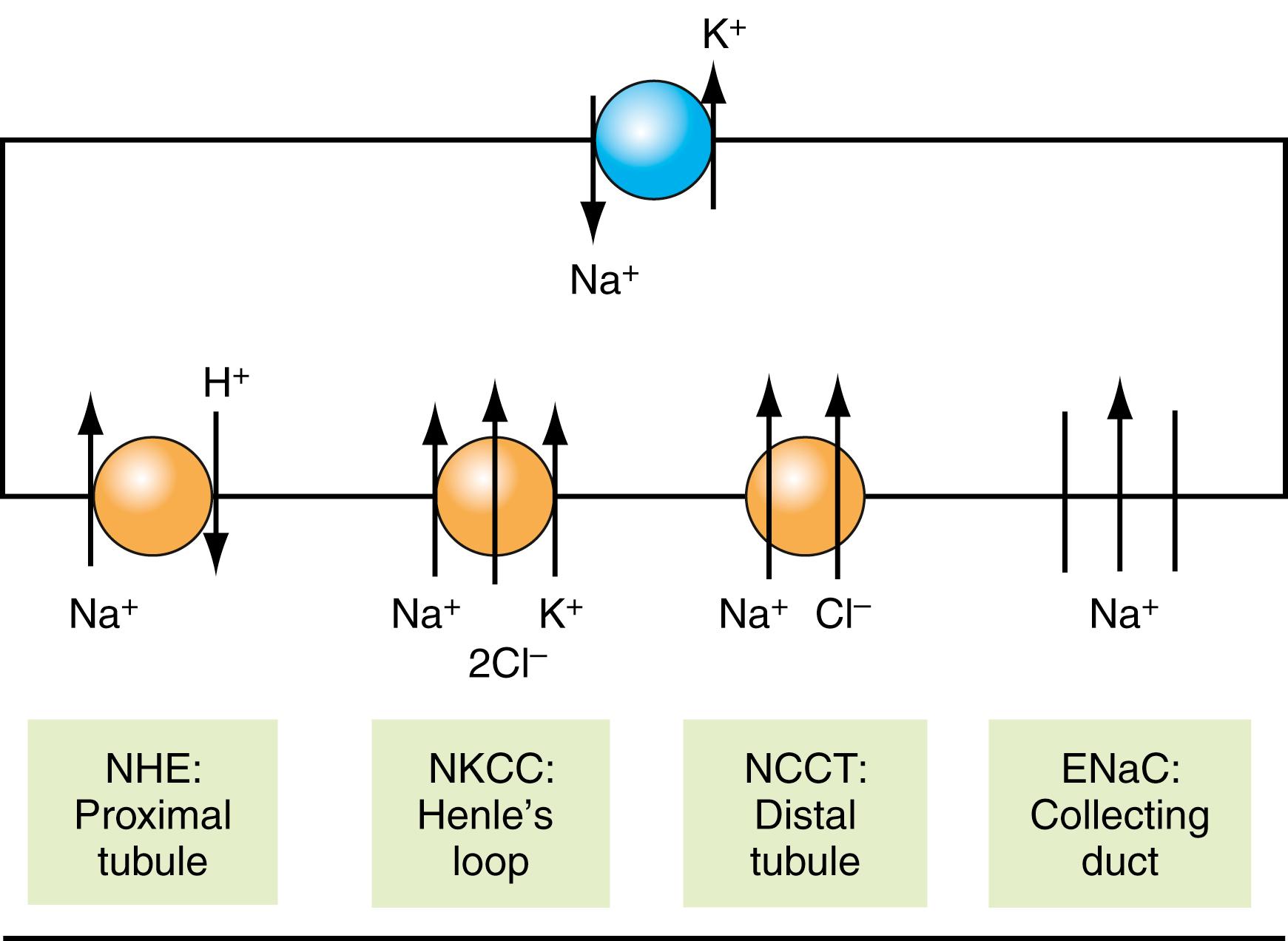
Some of the humoral substances that influence renal sodium excretion have an indirect effect on renal sodium output. For example, adenosine is currently the best candidate for the regulation of GFR through the tubuloglomerular feedback mechanism. Increased production of adenosine in response to a high NaCl concentration at the macula densa results in constriction of afferent arterioles, resulting in reduced GFR. The ultimate effect is reduced excretion of sodium. Likewise, constriction of efferent arterioles by angiotensin II can secondarily increase tubular reabsorption of NaCl, as the increased filtration fraction results in a higher peritubular oncotic pressure and a lower hydrostatic pressure.
Nonrenal Control Of Water And Electrolyte Balance
Insensible Loss of Water from the Skin
Water is lost from the skin primarily as a means of eliminating heat. Water loss from the skin without sweat is called insensible perspiration . Sweat contains about 50 mEq/L of sodium and 5 mEq/L of potassium. The maintenance of low NaCl concentration in the sweat requires the normal functioning of CFCR (chloride channel implicated in cystic fibrosis), and hence the loss of NaCl in sweat is greater in those with cystic fibrosis. Because the main purpose of water loss from the skin is elimination of heat, water loss from the skin depends mainly on the amount of heat generated in the body ( ):
Caloric expenditure depends on the basal metabolic rate and the rate of skin water loss may be sharply reduced in a cachectic malnourished person, especially an anuric person with impaired mental state.
Loss of Respiratory Water
The water content of inspired air is less than that of the expired air; hence, water is lost during normal ventilation. Because the ventilatory volume is determined by the amount of CO 2 production, which is, in turn, determined by the caloric expenditure, ventilatory water loss in normal environmental conditions depends also on caloric expenditure:
By coincidence, the quantity of water lost during normal respiration is about equal to the metabolic water production. Hence, in calculating water balance, respiratory water loss may be ignored in the measurement of insensible water loss provided that metabolic water gain is also ignored. Respiratory water loss increases with hyperventilation or fever disproportionately to metabolic water production ( ) .
Loss of Water in the Gastrointestinal Tract
The net activity of the gastrointestinal tract to the level of the jejunum is secretion of water and electrolytes. The net activity from jejunum to colon is reabsorption. Most of the fluid entering the small intestine is absorbed in the small intestine and the remainder is absorbed in the colon, leaving only about 100 mL of water to be excreted daily in the feces. The contents of the gastrointestinal tract are isotonic or slightly hypotonic to plasma, and any fluid that enters the gastrointestinal tract becomes isotonic. Thus, the loss of fluid from the gastrointestinal tract never causes hyponatremia but may cause hypernatremia in the absence of water ingestion ( ).
Measurement Of Renal Function
Concept Of Clearance
Renal clearance relates to the rate of urinary clearance of a substance in relation to the plasma concentration of the substance. It is defined as the theoretical volume of plasma that contains the substance excreted in the urine in a given period. In order to calculate the clearance, one must know the amount of the substance excreted in a given time period, which is calculated from volume and concentration. The next step is to know the plasma concentration of the substance (P x ) in order to determine the volume of plasma needed to account for the material excreted. For example, a person excreting 1500 mg of creatinine in a day would need 150 L of plasma to account for that 1500 mg of creatinine if the plasma concentration were 10 mg/L (1 mg/dL); creatinine clearance (C creat ), then, would be 150 L/day. At a plasma concentration of 100 mg/L (10 mg/dL), as in patients with renal diseases, only 15 L of plasma would be needed to account for the same 1500 mg of creatinine; C creat in this case would be 15 L/day. Customarily, clearance is expressed in m/min, but any volume and time units can be used. Thus, a clearance of 150 L/day is equal to 6.25 L/hour and 104 mL/min ( ). The formal equation for clearance is:
C x is clearance of a substance x , U x and P x are concentrations of the substance in urine and plasma, respectively, and V the volume of urine per unit time.
In estimating clearance, concentration and volume units must be consistent. For example, if urine creatinine concentration is 70 mg/dL and volume is 2000 mL/day, urine creatinine must also be expressed in mg/mL, not mg/dL. Thus, the total amount excreted is 0.7 mg/mL × 2000 mL/day = 1400 mg/day.
A clearance in mL/24 hours can be converted to a clearance in mL/min by the dividing the value by 1440, since 24 hours equals 1440 minutes.
Quick Formulas for the Calculation of Clearance
When calculating a 24-hour clearance in mL/min, urine creatinine excretion may be expressed in g/24 hours instead of mg/24 hours while expressing the plasma creatinine as mg/dL instead of mg/mL as long as the incorrect use of these units is corrected by multiplying the final result by 1000 (for using g instead of mg) and then by 100 (for using mg/dL instead of mg/mL). A further correction requires dividing the value by 1440 in order to convert a 24-hour clearance value to a value in mL/min as follows ( ):
Conversion of Clearance in L/Week to mL/min ( )
The conventional unit for clearance is mL/min; however, in certain situations, different units are more useful. For example, when one compares clearances of peritoneal dialysis in a patient on a CAPD (continuous ambulatory peritoneal dialysis) program with clearance in hemodialysis, the clearance unit often used is L/week. A patient on CAPD treatment typically has 2 L of dialysate exchanged every 6 hours. Since the volume drained is usually about 2.5 L (a slightly higher volume because of transudation of fluid from the blood to peritoneal cavity), creatinine clearance is about 10 L per day, or 70 L per week. As comparison, hemodialysis provides about 48 L of creatinine clearance with each treatment, or 144 L of clearance per week since usually 3 treatments are given each week. If weekly clearance in L/week is to be converted to mL/min, the following shortcut may be useful.
For example, 70 L/week of clearance is equal to 7 mL/min of clearance.
Measurement Of Glomerular Filtration Rate
GFR is generally considered the best overall indicator of the level of kidney function. Two different approaches have been utilized for the measurement of GFR. One approach has been to use an endogenous substance and the other to use an exogenous substance. It is important that whatever molecular marker is used to determine GFR, the substance is minimally reabsorbed and minimally secreted by the renal tubules.
Measurement of Glomerular Filtration Rate With Exogenous Substances
Inulin clearance is widely regarded as the gold standard for measuring GFR. Inulin clearance in healthy young adults has a mean value of 127 mL/min/1.73 m 2 in men and 118 mL/min/1.73 m 2 in women. GFR declines with age. After age 20 to 30 years, GFR decreases by approximately 1.0 mL/min/1.73 m 2 per year. The classic method of inulin clearance requires an intravenous infusion and timed urine collections over many hours. Inulin is expensive and the procedure is very time consuming and so is generally not performed clinically.
Consequently, a number of alternative measures for estimating GFR have been introduced. The urinary clearance of exogenous radioactive markers such as 125 I-iothalamate and 99m Tc-DTPA (metastable technetium 99 labeled diethylene triamine pentaacetic acid) provides good measures of GFR. Plasma disappearance of exogenous substances such as iohexol and 51 Cr-EDTA has also been used to estimate GFR; an advantage of this method is that it does not require urine collection. However, plasma clearance methods are not as accurate as those that require urine collection. GFR has also been measured with nonradiolabeled iothalamate in blood and urine. An obvious advantage of this method is avoidance of radioactive materials ( ; ; ).
Measurement of Glomerular Filtration Rate With Endogenous Substances
Endogenous substances that are widely used to determine GFR include urea, creatinine, cystatin C, beta trace protein, beta-2 microglobulin, and tryptophan glycoconjugate. The first two are widely used in clinical practice mainly because of their ready availability, but cystatin C is gaining popularity.
Creatinine as Measure of Renal Function
Creatinine is an endogenous substance with a molecular weight of 113 Da. It is produced by the muscle from creatine and creatine phosphate by a nonenzymatic dehydration process. The rate of production of creatinine is proportionate to the creatine-creatine phosphate pool, which, in turn, is proportionate to the muscle mass. An additional source of creatinine is creatine contained in ingested meat. The rate of in vitro conversion of creatine to creatinine in meat is dependent on temperature and acidity; high temperature and low pH increase conversion. Creatinine is the most widely used marker of GFR for several reasons. First, it is an endogenous substance with a fairly constant rate of production. Second, creatinine is not bound to plasma proteins; therefore, it is filtered freely by the glomerulus. It is not reabsorbed by the renal tubules, and only a small amount is secreted by the tubules ( ; ).
In the use of creatinine clearance, the inconvenience of urine collection and uncertainty of its completeness can be avoided by estimating the excretion rate. When renal function is normal and stable, creatinine excretion is almost equal to its production, which depends primarily on muscle mass. Muscle mass varies with sex, age, and body weight ( ). The creatinine production rate is estimated as age (A):
In both obese and wasted patients, this formula will overestimate creatinine production. Normally, creatinine excretion in urine is slightly less than its production because some creatinine is broken down by the colonic bacteria. The discrepancy increases progressively with decreasing renal function, because of the increasing fraction of nonrenal clearance of creatinine, which is about 0.04 L/kg/day. However, the metabolism of creatinine by the colonic bacteria is inducible and is increased more in chronic renal failure than in acute renal failure. Normally, a 70-kg man would have an extrarenal creatinine clearance of 2.8 L/day or 2 mL/min, less than 2% of the normal renal clearance. However, at a renal clearance of 4 mL/min, 2 mL/min of extrarenal clearance would represent one-third of the total plasma clearance of creatinine.
However, there are several drawbacks to the use of creatinine as a measure of GFR. First, although the rate of production in a given individual remains constant, it has substantial inter-individual variation, depending mainly on the muscle mass. In the presence of severe muscle wasting, production of creatinine could be reduced to less than 25% of the amount predicted from the body weight. Second, creatinine is also derived from dietary meat, and the quantity of meat ingestion can substantially influence the total daily production. Third, creatinine measurement is still frequently made by the alkaline picrate method (see later, more detailed, discussion), and a number of chromogens, both endogenous and exogenous, interfere with its measurement by this technique. Finally, creatinine is partially secreted by the proximal tubules via the organic cation transport pathway and tubular secretion is blocked by various drugs, including cimetidine, trimethoprim, pyrimethamine, and salicylate. The extent of tubular secretion varies with individuals and variation is much greater in the presence of renal dysfunction; tubular secretion could be as much as 50% of the amount excreted in the urine in advanced renal failure. In order to obviate the errors due to tubular secretion, creatinine clearance has been obtained with the simultaneous administration of cimetidine, which inhibits tubular secretion of creatinine. However, suppression of creatinine secretion by cimetidine is not complete and also has wide individual variations ( ).
Creatinine Measurement
Historically, the most widely used method of creatinine measurement has been the reaction of creatinine with picrate (2,4,6-trinitrophenol) at alkaline pH, described by Jaffe more than 100 years ago. More recently, enzymatic methods have been developed using creatinine amidohydrolase or creatinine iminohydrolase ( ). Creatinine is hydrolyzed by creatinine iminohydrolase to ammonia and N-methylhydantoin. The ammonia then combines with 2-oxoglutarate and NADH in the presence of glutamate dehydrogenase to produce glutamate and NAD+. The consumption of NADH, measured as a decrease in absorbance at 340 nm, is used to measure the concentration of creatinine. Creatinine can also be measured by converting creatinine to creatine by creatinine amidohydrolase. Creatine is then hydrolyzed by iminohydrolase and sarcosine oxidase to produce hydrogen peroxide. In the presence of horseradish peroxidase, 2,4-dichlorophenolsulfonate is converted to a colorless polymer by hydrogen peroxide. The concentration of the polymer is then measured at 510 nm.
Several substances—such as ketones, glucose, fructose, protein, urea, and ascorbic acid—also react with picrate and falsely increase creatinine concentration by Jaffe methods. Interference by glucose on creatinine measurement becomes significant when glucose concentration is very high, as in diabetic ketoacidosis or hyperglycemic coma. Glucose concentration is extremely high in dialysate fluid used in peritoneal dialysis; a correction for the high glucose is needed when creatinine concentration is measured in the effluent of peritoneal dialysate. The magnitude of glucose interference of creatinine measurement has been shown not only on glucose concentration but also on creatinine concentration. The interference by glucose in creatinine measurement does not occur in the enzymatic methods. Bilirubin and hemoglobin also interfere with the alkaline picrate method, resulting in falsely low values. Cephalosporin antibiotics also positively interfere with the alkaline picrate method, resulting in falsely elevated values ( ; ; ; ; ).
Without removing noncreatinine chromogens, the upper limit of normal measured by the Jaffe reaction is 1.6 to 1.9 mg/dL for adults. The upper limit of normal for serum creatinine measured after removing the chromogens is 1.2 to 1.4 mg/dL. Values for women are 0.1 to 0.2 mg/dL lower. When serum creatinine is very high, noncreatinine chromogens contribute proportionally less to the total reaction. With normal renal function, noncreatinine chromogens make up 14% (range 4.5%–22.3%) of the total; however, in advanced renal dysfunction, it contributes only about 5% ( ).
Use of Mass Spectroscopy in Creatinine Level Determination
Because of the possible interference of noncreatinine chromogens to the absorbance measurements for creatinine using the Jaffe method and because accurate creatinine measurements are required for computing the GFR as described elsewhere in this chapter, it has been recommended that all creatinine assays should be standardized by a validation procedure in which creatinine assay results on samples are correlated with the values obtained on the same samples using a gold standard method, which is mass spectroscopy based (see Chapter 5 ), called isotope dilution mass spectroscopy ( IDMS ) ( ). Results using this method are usually not affected by extraneous chromogens. In this method, in its simplest form, serum samples are extracted so as to separate creatinine from other serum components. A known amount of a C 13 isotope-enriched creatinine is then added to the sample. The mass spectrum of this sample is taken. The height (relative abundance) of the parent creatinine C 13 isotope peak represents the known concentration of the C 13 creatinine. This concentration is corrected for losses that may have been incurred in the extraction procedure using an internal standard. The corrected peak height (minus the corrected known height of unlabeled creatinine in the isotopically labeled creatinine) is then compared with the height of the corresponding parent peak of the sample creatinine, and the ratio of the two peaks is computed. Since the concentration of the C 13 -labeled creatinine is known, the concentration of the sample creatinine can be directly calculated. This procedure has the disadvantage of the extracted sample possibly containing compounds that may have a molecular mass that occurs at the unlabeled creatinine parent peak, which can result in overestimation of creatinine concentration. Currently, standardization of creatinine determinations has not been adopted universally, in part because the values obtained using IDMS are significantly lower than those obtained in patients who are being followed over prolonged times, making interpretation of results more difficult.
Cimetidine-Enhanced Creatinine Clearance
Tubular secretion of creatinine results in falsely elevated values in creatinine clearance, especially in renal insufficiency. Measurement of creatinine clearance with inhibition of tubular secretion with cimetidine substantially improves the creatinine clearance estimate of GFR in patients with mild to moderate renal impairment. However, tubular secretion of creatinine is not completely blocked by cimetidine; hence, the method still overestimates GFR ( ; ).
In addition to cimetidine, a number of other drugs also interfere with tubular secretion of creatinine by inhibiting organic cation transporters. These include trimethoprim, pentamidine, and amiloride ( ).
Formulas to Estimate Creatinine Clearance as an Estimate of Glomerular Filtration Rate
With the realization that accurate urine collection is a major limitation in creatinine clearance as a measure of GFR, attempts have been made to mathematically transform serum creatinine to estimate GFR. In part because of the convenience, these methods are widely used in clinical practice. The two most widely used formulas are the Cockcroft and Gault formula and the MDRD formula ( ):
where IBW is ideal body weight and SCr is serum creatinine concentration. IBW is calculated by the following formula:
The Cockcroft and Gault formula reduces the variability of serum creatinine estimates of GFR caused by a difference in creatinine production due to differences in muscle mass based on sex and age. However, because the formula does not take into account differences in creatinine production due to variation in muscle mass caused by disease states, it systematically overestimates GFR in individuals who have relatively low muscle mass in relation to their body weight, such as obese, edematous, or chronically debilitated subjects. Moreover, it does not take into account variations caused by extrarenal elimination and tubular secretion ( ).
In the Modification of Diet in Renal Disease (MDRD) study, Levey and coworkers measured GFR by I 125 -iodothalamate to derive a formula for estimating GFR using six variables: age, sex, race, serum urea nitrogen, serum creatinine, and serum albumin concentration ( ). In 2000, the same investigators produced a simplified MDRD formula based on 4 variables, serum creatinine, age, race, and sex. Few diabetic individuals were included in the original studies and these formulas tested in diabetic patients were found to be inaccurate ( ). Furthermore, the use of exponents in the formula has prevented routine use in clinical practice ( ). GFR calculators based on the equations below are now available online, facilitating these calculations.
MDRD formula (mL/min/1.73 m 3 ):
The simplified MDRD formula (mL/min/1.73 m 3 ) based on 4 variables (serum creatinine, age, race, and sex) (44):
where Cr = serum creatinine (mg/dL), Wt = body weight (kg), BUN = blood urea nitrogen (mg/dL), and Alb = serum albumin (g/dL). More recently, a modified GFR equation proposed by the CKD Epidemiology Collaboration, known as the CKD-EPI formula, has been added to the consortium of formulas to calculate estimated GFR (eGFR) ( ). Despite the claim that this formula more accurately predicts eGFR than the original MDRD equation, errors caused by variability in serum creatinine concentration due to individual variations in creatinine production remain unresolved.
Whereas the Cockcroft and Gault formula includes the body weight, the MDRD formula does not include the body weight, because the result of the latter is expressed in mL/min/1.73 m 3 rather than an absolute value. The same errors resulting from variations in creatinine production rate caused by disease states are not eliminated in the Cockcroft and Gault formula as well as the MDRD formula. Both the Cockcroft-Gault and MDRD formulas estimate GFR in adults and are not applicable to measurement of GFR in children, obese, bedridden patients, or amputees. Following are the formulas used most often for estimating creatinine clearance for children:
Schwartz formula:
Counahan Barrett formula:
In 2009, Schwartz et al. further modified their formula to estimate GFR more accurately in children. The new formula is very similar to the MDRD equation in that it uses multiple exponential functions; the use of the formula requires knowing values of serum creatinine, height, BUN, and serum cystatin C. Like the MDRD formula, a computer program is usually needed to use the formula ( ; ).
Modified Schwartz formula:
In addition, the Chronic Kidney Disease Epidemiology Collaboration (CDK-EPI) group has an alternate equation that can be used to compute GFR values for GFRs > 60 mL/min per 1.73 m 2 ( ).
It has been shown that GFR estimated from these various formulas is not very accurate. However, creatinine clearance values estimated from the formulas are still more accurate than those from direct measurements mainly because of the inaccurate urine collections and variations in plasma creatinine concentration in the latter. Consequently, K/DOQI (Kidney Disease Outcomes Quality Initiative) guidelines have recommended the use of these formulas in calculating creatinine clearance instead of direct measurements ( ).
All of these formulas are useful in the estimation of GFR in chronic states when creatinine production is assumed to be equal to the amount excreted in the urine. In acute renal failure when serum creatinine rises rapidly during the development of renal failure and falls rapidly during the recovery phase, such an assumption is invalid. Hence, the estimation of GFR by either method is invalid. Measurement of creatinine in the urine with timed urine collection is more useful in determining creatinine clearance in acute renal failure.
Urea as Measure of Renal Function
Urea is the main waste product of nitrogen-containing chemicals in the body. It has a molecular weight of 60 Da. However, by custom, the concentration of urea is expressed only by the nitrogen content of urea. For this reason, the term serum or urine urea nitrogen is widely used in place of serum or urine urea . Because a molecule of urea contains 2 nitrogen atoms, the molecular weight of urea nitrogen is 28 Da ( ).
Serum urea is widely used as a measure of renal dysfunction, but its value as a measure of GFR is not very good for several reasons. First, urea concentration in the serum depends not only on the renal function but also on the rate of urea production, which depends largely on protein intake. The rate of protein intake varies widely from individual to individual.
Urea is freely filtered at the glomerulus but is reabsorbed substantially in the proximal convoluted tubule and the inner medullary collecting duct. Reabsorption of urea in the proximal tubule occurs passively through the lipid membrane without the help of urea transporters, whereas in the inner medullary collecting duct, urea reabsorption is mediated by urea transporters. Some of the urea reabsorbed from the inner medullary collecting duct then reenters the tubule in the thin descending limb of the cortical nephrons, which also express urea transporters. The amount of urea reabsorbed in the proximal tubule varies greatly depending on the status of effective vascular volume; reabsorption is markedly increased in states of volume depletion because the luminal concentration of urea is high owing to the increased fractional reabsorption of salt and water. The amount reabsorbed in the inner medullary collecting duct is increased when urine osmolality is high because of the high urea concentration. For these reasons, urea clearance does not reflect GFR accurately, but serum urea nitrogen is still widely used as a measure of renal dysfunction. In the presence of normal renal function without volume depletion, urea clearance is about 50% of creatinine clearance, but in the presence of severe volume depletion, its clearance could be as little as 10% of creatinine clearance. In advanced renal failure, urea clearance approaches unity with GFR and is better than creatinine clearance as a measure of GFR ( ; ).
Measurement of Urea
Essentially, there are 3 methods for the measurement of urea. The gold standard, which is used only as a reference method because of its high cost, is isotope dilution mass spectrometry. In clinical laboratories, urea is measured either by the colorimetric method based on a reaction of urea with diacetyl monoxime or by enzymatic methods. In the former, urea reacts directly with diacetyl monoxime under strong acidic conditions to produce a yellow condensation product. The reaction is intensified by the presence of ferric ions and thiosemicarbizide. The intense red color formed is measured at 540 nm ( ; ).
The initial reaction in all enzymatic methods is hydrolysis of urea by urease, which produces ammonia and CO 2 . Ammonia and CO 2 produced are measured by various methods to calculate the concentration of urea in the original sample. Measurement of ammonia is most often used. In one of these methods, ammonia produced by urease converts glutamate and ATP to glutamine and ADP. The ADP so produced is consumed in reactions catalyzed sequentially by pyruvate kinase and pyruvate oxidase to generate hydrogen peroxide. The hydrogen peroxide is then measured as an indirect estimate of urea concentration. In another enzymatic method, as in the one used for creatinine described in the preceding section, ammonia produced from urea hydrolysis reacts with alpha-keto-glutarate and NADH to produce glutamic acid and NAD + by glutamate dehydrogenase. The amount of NADH consumed is measured photometrically to determine the urea concentration. Another urease method involves the indophenol method, in which ammonium produced by urease reacts with hypochlorite to form monochloramine. In the presence of phenol and an excess of hypochlorite, the monochloramine forms a blue-colored compound, indophenol, the concentration of which is determined spectrophotometrically at 630 nm. In yet another enzymatic method, CO 2 produced by urease is measured by thermal conductivity gas chromatography.
Other Measures of Glomerular Filtration Rate
You're Reading a Preview
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here
