Physical Address

304 North Cardinal St.
Dorchester Center, MA 02124

Epidemiology: science for the art of medicine


Introduction

The term epidemiology has its roots in Greek words meaning, very roughly, ‘a discourse about something visited on the people’. Whilst it is clearly a close cousin of ‘epidemic’, it is important to understand how the two relate to each other. Epidemic , though commonly understood to mean an outbreak of infectious disease, is more strictly defined as the prevalence of a disease among populations or groups of people at a particular time, and produced by special causes not usually present in the affected locality. Pandemic refers to an outbreak of a disease over a very large geographic area, and affecting a high proportion of the population. The realm of epidemiology, however, is wider and more complex than the mere study of epidemics.

In clinical medicine, the focus is on the individual, the symptoms and signs of the illness, its diagnosis, and subsequent decisions about therapy. Epidemiology, on the other hand, investigates patterns of disease among populations or groups of people to understand causation and determine appropriate responses. Definitions and explanations of many of the terms that are used throughout this chapter are given in Table 7.1 .

Table 7.1
Terms used in epidemiology
Allele Genes exist in different allelic forms defined by differences in nucleotide sequence
Allocation concealment The inability to predict or discover the potential random allocation group until the point of assignment
Alternative hypothesis (H 1 ) A statement that is different from the null hypothesis and that is true if the null hypothesis is false
Bias A systematic difference between the observed and true effect
Binary data Have two possible values. For example, yes or no, up or down. These data are represented mathematically by the binomial distribution
Case–control study A study where diseased individuals (cases) are identified and compared with individuals who are as similar as possible as the cases except that they do not have the disease (controls)
Clinical trial An experiment involving humans used to evaluate a new treatment in relation to a particular clinical outcome
Cohort study A study in which a group of individuals without the outcome of interest (disease) is followed over time (usually prospectively) to investigate the effect of their exposure to a risk factor on outcomes in future
Collinearity When two factors are very strongly associated
Confidence interval A range in which we are confident (to a specified extent) that the true population parameter lies
Confounding Occurs when we are looking at a relationship between two factors and a third factor (the confounding variable) masks or exaggerates the observed relationship between the two because that third factor is associated with both the other factors
Contingency table A table which contains frequencies in ‘cells’
Correlation coefficient The extent of the relationship of the points to a straight line
Crude rate A measure made without adjustment for other factors, such as age, that otherwise may be misleading
Degrees of freedom A measure of how many numbers in the table are free to vary without affecting the totals. In a 2 × 2 table, provided the totals remain the same, only one number at a time is free to vary. As soon as this number is changed in one cell, the numbers in the other cells are forced to change. There is therefore one degree of freedom in a 2 × 2 table
Fisher's exact test A method that evaluates all possible tables with the same totals as if the null hypothesis was true
Histogram A graphical display of frequencies in separate categories of data. Frequencies are represented as bars, the area under the bar denotes the frequency (unlike bar charts where the height of the bar denotes the frequency). (Greek origin: histos, upright as in a vertical ship's mast, gramma a record or writing)
Incidence Measure of the number of new cases of a disease, occurring during a specified period of time in a specified location
Interdecile range The central 80% of the ordered data (between the 10ths, or 10th percentile and 90th percentile)
Interquartile range The central 50% of the ordered data (between the quarters or 25th percentile and 75th percentile)
Kappa The proportion of agreement in a classification beyond that due to chance in relation to the potential agreement beyond chance, where a value of 1 implies perfect agreement and a value of 0 no better than chance alone
Likelihood ratio (LR) A ratio of two likelihoods, for example a ratio of the chances of getting a particular test result in those having and not having the disease
Matching A process of selecting individuals who are similar in characteristics known to be associated with the outcome but which are not of interest. Most common are age and sex, which are known to be associated with many diseases
Mean or arithmetic mean A measure of the centre of the data obtained by summing the individual values and dividing the total by the number of data points
Median (or 50th percentile) When data are put into rank order the median divides the data into two equal parts. For example, if there are 9 data points, the fifth in rank order will be the median, four datum points being below, and four above. If there are 10 datum points then the fifth and sixth, in rank order, will be in the middle. Traditionally, the median of those two numbers is given by their mean
Minimisation Selection of an individual based on minimising the chance that the selection will unbalance the group for a particular factor
Mode The item that is the most common in the data set
Null hypothesis (H 0 ) A statement that assumes no difference or effect
One-tailed Where the alternative hypothesis specifies a direction to the effect
Outcome or dependent variable The characteristic or outcome of interest that is affected by one or more variables
Percentile Division of ordered data into 100 equal parts. The median is the 50th percentile
PPV or positive predictive value of a test The probability of actually having the condition when the test for the condition is positive. Sometimes referred to as the OAPR (odds of being affected given a positive test result)
Predictor or independent variable An attribute that can have an effect on the outcome
Prevalence Measure of the number of existing cases of a disease at a particular point in time (point prevalence) or over a specified period of time (period prevalence), in a particular place, divided by the total population
Prospective study One where individuals are followed forward in time
Random Selection of a subject or item from a population such that the chance of being selected is the same for all subjects or items within that population
Randomised controlled trial A clinical trial in which individuals are allocated to the different treatment groups in a randomised fashion
Retrospective study A study in which what has happened in the past to individuals enrolled in the study is investigated
Sample A subgroup of a population being studied
Sampling frame A list of all individuals within a population
Scattergram Plot of one variable against another with each pair of measurements represented by a point
Selection bias Bias that occurs when the individuals being studied are not representative of the population of interest
Sensitivity The proportion of people with a disease who are correctly identified by the diagnostic test (true positives). Sometimes referred to as the ‘detection rate’. If a test is not 100% sensitive then there will be false-positive results
Sign Manifestation of a target disorder perceived by the clinician during an examination
Specificity The proportion of people without a disease who are correctly identified by the diagnostic test (true negatives). If a test is not 100% specific then there will be false-negative results
Standard deviation A measure of the spread of numerical (continuous or discrete) data
Standard error A measure of how precise the summary statistic is. The standard error of a proportion is a measure of how sure we are about an observed proportion
Standardise To adjust a rate to allow comparison between different populations
Standardised mortality ratio (SMR) Ratio between observed and expected number of an event (such as death) multiplied by 100 and computed by indirect standardisation
Stratification Selection of a subgroup that has similar characteristics
Symptom Manifestation of a target disorder perceived by the patient, spontaneously or on questioning
t -distribution A continuous distribution with a shape similar to the normal distribution. It is used to make inferences about means
Two-tailed A test in which the alternative hypothesis does not specify a direction to the effect

The Epidemiological Approach

In diagnosing and managing the illness of particular patients, clinicians rely not only on their own experience, but also on knowledge and understanding derived from other clinicians' observations of patients with similar signs, symptoms and laboratory findings. For example, the observation of groups of children with whooping cough led to the understanding of how this disease develops ( Information box 7.1 ).

Information box 7.1
Whooping cough

Whooping cough begins with symptoms similar to a common cold. After an incubation period of 7–10 days, an irritating cough progresses to spasms, or paroxysms, of coughing, sometimes accompanied by a characteristic ‘whoop’, particularly in young children. The coughing spasms may be followed by vomiting and could last for 2–3 months – hence the term ‘100-day cough’. Severe complications such as dehydration, brain damage or death may occur, particularly in infants under 6 months old. The disease is transmitted by droplets and is highly infectious. Diagnosis is usually made from the history and symptoms, but may be confirmed by isolating Bordetella pertussis from the sputum. The problem for clinicians can be that their own direct experience of whooping cough is limited, so that they will need to draw on the collective story. The rarer the condition, the more important this is.

The selection of effective treatments depends on an understanding of how similar patients fared on different treatments in the past.

Epidemiology provides a scientific framework for understanding how health problems occur, how diseases behave and whether interventions are effective. In a clinical context, epidemiology also provides a better understanding of the issues that can inform further research to develop more effective strategies for reducing disease incidence (see later) and improve health.

Epidemiology as the detective

By careful and accurate descriptions of observed phenomena and by logical comparisons of these phenomena, epidemiology seeks to describe the natural progression of disease and epidemics, and identify factors that may have a causal relationship with diseases. This knowledge contributes to the understanding of how diseases and epidemics arise so that strategies for controlling and preventing epidemics and for treating disease may be formulated. The classic example is the work of John Snow and the Broad Street Pump.

The Broad Street pump

In 1855, Dr John Snow published his treatise on the mode of communication of cholera (Greek cholé bilea; a highly infectious disease characterised by profuse vomiting and diarrhoea). The ‘cholera morbus’ was first described near Jessore, India, in 1817. In 1823, it had spread to Russia; by 1831 it was in Hamburg, and the first case in east London was identified on 12 February 1832. In contrast, H1N1 (influenza A, or swine flu) virus emerged in the spring of 2009 and within 1 month cases had been reported in 48 countries, with up to 90 million people being affected in 74 countries worldwide before the pandemic was over, reflecting its person-to-person transmission and global human movement.

Variously called ‘Asiatic’, ‘spasmodic’, ‘malignant’, ‘contagious’ and ‘blue’, cholera was also confused with ‘common’ or ‘English’ cholera, dysentery and food poisoning. Although the general populace believed the disease to be contagious, its exact nature was much debated among the medical profession. A large proportion actually thought that the disease did not spread from person to person but could arise spontaneously, as a result of bad air. The popular London Medical Gazette agreed that there was a serious problem but simply discussed its prevention and cure, rather than the origin of cholera or its causes.

John Snow was prompted to study ‘The most terrible outbreak of cholera which ever occurred in this kingdom’. This took place in Broad Street, Golden Square, in the centre of London's West End in 1854. Within the space of 10 days more than 500 people had died and most others had fled the area ( Table 7.2 ).

Table 7.2
Reported attacks of cholera in Broad Street, Golden Square in Soho, in the West End of London, published by John Snow in 1854; 545 deaths occurred between 1 and 11 September
Month Date Number of fatal attacks Deaths
August 19 1 1
20 1 0
21 1 2
22 1 0
23 1 0
24 1 2
25 1 0
26 1 0
27 1 1
28 1 0
29 1 1
30 6 2
31 56 3
September 1 143 70
2 116 127
3 54 76
4 46 71
5 36 45
6 20 37
7 28 32
8 12 30
9 11 24
10 5 18
11 5 15
12 1 6
13 3 13
14 0 6
15 1 8
16 4 6
17 2 5
18 3 2
19 0 3
20 0 0
21 2 0
22 1 2
23 1 3
24 1 0
25 1 0
26 1 2
27 1 0
28 0 2
29 0 1
30 0 0
Date unknown 45 0
Total 616 616

Snow had already published a report suggesting that cholera was spread by contaminated water. Cholera, he noted, ‘always commences with disturbances of the functions of the alimentary canal’, and he suggested that it was spread by a poison passed from victim to victim through sewage-tainted water. Neither the authorities nor other members of the medical profession were persuaded by his theories, but the 1854 outbreak gave him a further opportunity to prove his thesis.

Because most of the deaths appeared to have occurred close to the water pump in Broad Street, Snow took the view that this was the source of the problem. He examined the water and at first saw nothing suspicious, but over a few days noted that the quality of the water varied, and that it seemed to have small white flocculent particles floating in it. At this point, he decided to undertake a systematic survey of the deaths in the vicinity. Eighty-three deaths, mapped according to place of residence, had occurred within 3 days at the beginning of September in the three sub-districts that surrounded the Broad Street pump ( Fig. 7.1 ) .

Fig. 7.1, Map of deaths in Soho showing that reported deaths from cholera clustered around the Broad Street pump.

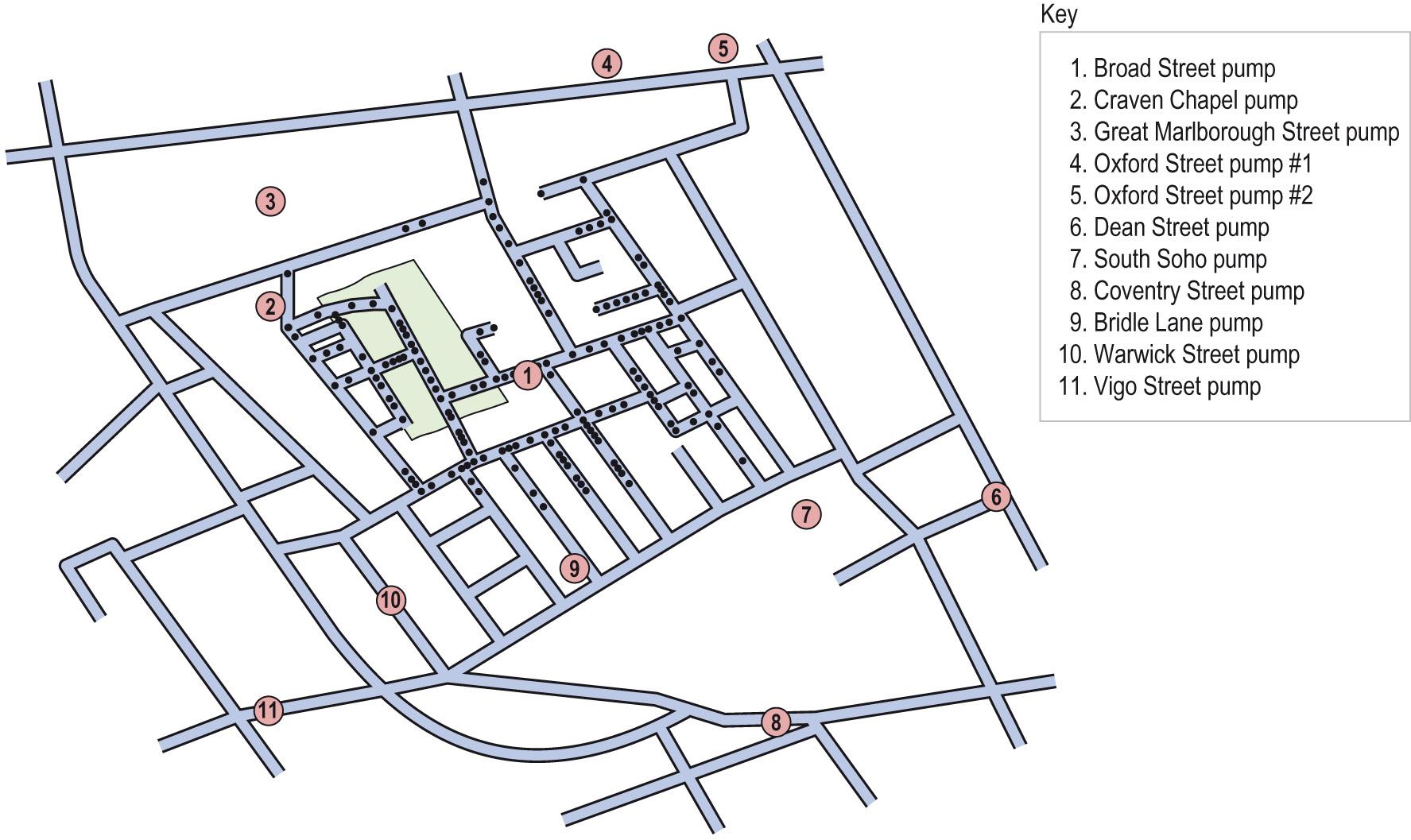
In virtually all cases, the Broad Street pump was the closest to the victims' home. Where this was not so, affected individuals were regular users of the Broad Street pump in preference to others closer to where they lived. Only two cases were exceptions to this pattern and these might in any case have been examples of the low incidence of cholera that was normally to be expected in London at this time. Within the area, however, were industries, breweries and workhouses where the workers were generally shown not to have developed the disease. Snow questioned the owners and found that each establishment had its own separate source of water, or, in the case of the brewery, the workmen only drank the malt liquor made using deep well water. The pump had a reputation for ‘better’ water and ‘was widely used for mixing with spirits in all the public houses around. It was used likewise at dining-rooms and coffee-shops’. Dr Snow deduced, by inference, that the most likely source of the infection was the pump.

After presenting his evidence, Dr Snow persuaded the authorities to remove the pump handle, after which no new cases of cholera were reported. The pump well was examined, but there was no defect that would suggest the reason for the contamination of the water, and the local sewer was too far away. The whitish particles that Snow saw were examined under the microscope by Dr Arthur H Hassall, a contemporary physician, who thought they were just decomposition of another matter. The water, however, even when clear, smelt offensive and Dr Hassall noted ‘a great number of very minute oval animalcules in the water’, which he declared to be of no importance.

It would be some years before the causal agent, bacterium Vibrio cholerae, was formally identified, but Snow did unearth the probable cause of the outbreak. Just before the epidemic, a child living in Broad Street had been taken ill with symptoms of cholera. The nappies had been steeped in water to be washed, and the water was subsequently tipped into a leaking cesspool, just 1 m from the Broad Street well.

Causal association by inference

A later example that causal association by inference may not identify the actual cause of the disorder is that of peptic ulceration . For many years, peptic ulceration was attributed to over-secretion of gastric acids, over-indulgence of alcohol, tobacco smoking, stress and various other lifestyle factors, all by inference. Treatment was by the administration of antacids, various lifestyle modifications and surgery, including partial gastrectomy and vagotomy. It was not until 1982 that two Australian scientists, Barry Marshall and Robin Warren, identified the Gram-negative bacterium Helicobacter pylori as the actual cause of gastric and duodenal ulcers and gastric cancer. Treatment for peptic ulcers is now a 2-week course of antibiotics.

Patterns of life and death

To understand the ‘health’ of populations, observation and recording of events relating to ill health or death provide the information that is needed. These events arise naturally, rather than as the result of experimentation; for example, to see if a vaccination programme for whooping cough actually reduces the incidence of whooping cough. Descriptions of the information (data, statistics) collected through observation are the cornerstone of public health, where:

  • Morbidity refers to the incidence (see later) of a disease or all diseases in a population. Newspaper headlines declaring that more than 130 000 people will be diagnosed with colon cancer tell us little unless put into a context – over what period of time, and in what sized population?

  • Mortality refers to the death rate in a population, which may be from all causes, i.e. the ratio of all deaths to the total population, or for a specific population, e.g. infant mortality rate refers to the ratio of the number of deaths of infants under 1 year of age to the total number of live births in a population in a particular year, or for a specific condition.

Descriptive studies

The essential components of descriptive epidemiology are concerned with people , time and place . Epidemiological methods are used to make inferences based on descriptions of groups of people, or populations, rather than individual patients. These groups have shared characteristics, which could be geographically defined (e.g. living within 2 km of pylons or nuclear power stations, or living in the vicinity of the Broad Street pump); defined by a common condition (such as coronary heart disease, childhood leukaemia, cholera); associated with possession, or lack, of a particular gene (such as in Alzheimer disease); or shared personal attributes such as age, sex, racial origins, occupation, social class or lifestyle behaviour (e.g. tobacco smoking, alcohol consumption). Such characteristics may be used to identify and investigate differences in patterns of disease, and generate hypotheses about causal association, evaluate the effectiveness of treatment, plan health service provision or ask further questions. Note that this does not identify the actual cause of the condition but possible factors that are associated with the disease phenomenon (see earlier).

Descriptive studies use collected information to examine a population, either at a single point in time or over a period of time, looking at long-term trends, cyclical change or the kinds of sudden change associated with epidemics ( Information box 7.2 ).

Information box 7.2
An epidemic of birth defects

Birth defects are distressing, but thankfully rare. A single example can appear to a clinician to be nothing more than an isolated and random occurrence. The following story illustrates the importance of clinicians reporting unusual events such as these in order to contribute to a broader epidemiological understanding.

Thalidomide (α-phthalimido-glutarimide) was produced by the German company Chemie Grünenthal and supplied under the name Distaval in the UK, originally as an anticonvulsant, but later as a sedative, and was widely prescribed to women to combat symptoms common in early pregnancy. An apparent advantage – that overdoses did not result in death – led to its wide promotion, not only as a sedative, but in combination with other drugs for a wide range of common medical conditions.

In Germany, where thalidomide was available over the counter, two apparently similar cases of amelia , an unusual congenital absence of long bones in a limb or limbs, were first reported at a paediatric meeting in 1960. A year later, a clinician described 13 cases that had been referred to him over the previous 10 months, describing a variety of severe malformations seen in these children and remarking that the occurrences had the appearance of an epidemic. By the end of 1961, Lenz had reported that a common factor in these cases was that the mother had taken thalidomide. The same suggestion was reported from Australia and later confirmed throughout many Western countries. Fewer cases were seen in the USA because, as a result of early side effect reports from Europe, the drug had not been passed for general use there. Thalidomide was withdrawn from use in the UK in November 1961.

Measuring disease occurrence

Epidemiological methods make it possible to estimate the risk (chance, probability) within a group of people of the disease developing. To define disease occurrence, two important concepts are used: incidence and prevalence .

Disease incidence

Incidence is concerned with new cases of disease. The number of events (e.g. heart attacks) that are new cases occurring during the specified time (5 years) in a defined population (e.g. overweight male smokers aged 45–55) and resident in a particular geographical location is referred to as the incidence .

Disease prevalence

Prevalence is concerned with the number of people having the problem at one time and is another way of measuring disease occurrence. It is the total number of people with the disease (heart attack, new or old) over the specified time (5 years) in the population (overweight male smokers aged 45–55).

Rates and relationship between incidence and prevalence

A simple count of the kind described previously does not really describe the size of the problem, however, because the same number will have different significance in populations of different sizes. Five cases in 50 is clearly very different from 5 in 5000. This is why it is more useful to think in terms of rates.

Prevalence is a measure of the burden of the disease. As new cases are added, so the incidence increases; these new cases add to the burden of the disease (prevalence) until the patient is cured or dies. A chronic condition such as rheumatoid arthritis would have few new cases in a year (low incidence) but a higher total number of cases (high prevalence), as there will be many more cases diagnosed in previous years. Prevalence of a particular condition, therefore, varies with incidence and the likely duration of the condition:

Prevalence=incidence×duration(in which duration isdetermined by the cure rate and the death rate)

If there is more disease (increased incidence), assuming that its duration is unaffected, so prevalence must also increase. On the other hand, if the disease decreases in incidence, so does prevalence. This balance can be affected by altering the duration. Treatment can affect prevalence differently. If it successfully prevents deaths it can increase the duration of the disease and therefore increase prevalence. If treatment is so successful that is provides a cure, so the duration of the disease will decrease, reducing prevalence. The burden of disease is an important consideration when planning health provision.

Measuring disease outcome

With the exception of death, which is usually unequivocal, measuring health outcomes can be difficult because of individual differences in the understanding of health-related terms. The assessment of causes of death and the diagnosis of stroke are just two examples that may be recorded differently by different clinicians. In these circumstances, different estimates of disease incidence may simply reflect differences in definition rather than in the frequency of events. This means that case definition becomes important when collecting information, so that there is unequivocal shared understanding of the way a case is defined. A case of high blood pressure, for example, may be defined as ‘a person with an average blood pressure >140/90 mmHg from three readings over a period of no more than 2 years’.

If patterns of morbidity and mortality are to be established, the collection of data needs to be reliable and accurate, and this is not without its difficulties ( Information box 7.3 ). Many data depend on clinicians' vigilance, recording of observations and diligence in notification. Mandatory systems for reporting disease, birth and death are in place in all developed nations. The World Health Organization (WHO) publishes and updates morbidity and mortality information worldwide ( http://www.who.int/en/ ). In the UK, some notifications of disease are required by law, whereas others are voluntary. Other types of data result from large-scale surveys and government initiatives, such as the General Household Survey and the UK decennial population census. The last census was in 2011 and, with increasing cost, decreasing compliance and the need for more regular updates, the ‘Beyond 2011 Programme’ was established. In 2015, it was recommended that there should be a decennial census in 2021 but, where possible, the collection would take place electronically. Individual clinicians are mainly involved with reporting on births, congenital anomalies, abortions, deaths, cancers, communicable diseases and adverse drug reactions. This information is vitally important for understanding the trends and patterns of diseases, and, in the UK, it is also used to monitor the performance of the National Health Service (NHS).

Information box 7.3
Common problems with routinely collected data

  • Absence of information : important information from individuals, such as occupation, which may be relevant to the presence of a particular disease, may often not be reported, or not reported in sufficient detail.

  • Inconsistent information : in countries where death registration is standard practice, mortality measures can be reliable, but measures of morbidity can be more difficult because different points of reference may be variously recorded, such as onset of symptoms, onset of disease, first diagnosis, first hospital admission.

  • Case ascertainment : information about numbers of people with a particular disease may be influenced by the extent to which the condition comes to the attention of the medical profession, and this may also be related to the availability of medical services. In addition, some debilitating chronic conditions may not always be managed medically, and so not brought to the attention of general practitioners, and if a condition does not directly cause death, it will not be recorded on the death certificate.

  • Diagnostic criteria : diagnosis produces many difficulties that can lead to inaccuracy in data collection – inadequate definitions, inadequate diagnostic facilities and diagnostic procedures not being carried out routinely, or not applied to the whole population. In addition, there may be changes in the International Classification of Diseases (ICD). For example, in 2001, the WHO lowered the threshold for the diagnosis of diabetes mellitus in pregnant women (gestational diabetes mellitus (GDM)). Although this made little difference in the UK population as a whole, in the London borough of Newham, where South Asians at high risk of GDM form over 30% of the population, the numbers diagnosed almost doubled.

  • Variable formats for data : some data may be presented in records that are not suitable for classification because of lack of information or detail. Some data may be inaccessible for confidential reasons.

Births and deaths

The civil registration of births and deaths is compulsory in the UK, as in many countries, where someone (usually parent or relative) has to register the event with local registrars. Births have to be registered within 42 days in England, Wales and Northern Ireland and 21 days in Scotland. Other information required in birth registration includes the date and place of birth and occupation of the father, mother, or both parents depending on circumstances.

Deaths have to be reported within 7 days. Infants born dead after 24 weeks' gestation are registered as stillbirths . Infants born alive who die have to be registered as both a birth and a death. Death certificates are filled in by the attending doctor, who has to give accurate details of each death.

Terminations of pregnancy under the 1967 Abortion Act have to be reported on a prescribed form to the chief medical officers of England, Wales and Scotland within 7 days. Data are published by the Office of National Statistics (ONS) ( https://www.ons.gov.uk ). The Act does not apply in Northern Ireland although, as a consequence of the death of a woman refused an abortion, termination was permitted after 2013, but only in exceptional circumstances: when the woman is at risk of taking her life, or at risk of dying as a result of medical complications. It is still not allowed in cases of rape, incest or foetal abnormalities. Political devolution has meant that this situation is unlikely to change in the near future; a vote to support abortion in the case of foetal abnormality was voted down in 2014 and, although there is public support, only a minority party supports a change. The Supreme Court has also ruled that termination will not be allowed for these women in other parts of the NHS and it is likely that this decision will be considered by the European Court of Human Rights in the future.

Confidential enquiries

Enquiries into deaths in some special categories are made through confidential enquiries , when information from anonymised case notes and reports from the professionals who looked after the deceased are reviewed by panels of relevant experts. Unlike audit, patient details are critically reviewed anonymously, and findings about the standards of care are published. The panels try to determine whether the deaths were ‘avoidable’, whether the quality of care given was of an acceptable standard and whether lessons can be learned. In the past, there was no attempt to compare the standards of care between regions or to establish a contemporary standard of care. National level confidential enquiries include:

  • Confidential Enquiry into Maternal and Child Health (CEMACH) – a system for maternal and perinatal mortality surveillance to identify avoidable factors with the aim to improve health care for mothers and babies.

  • Centre for Maternal and Child Enquiries (CMACE).

  • Mothers and Babies Reducing Risk Through Audits and Confidential Enquiries across the UK (MBRRACE-UK)

  • National Confidential Enquiry into Suicide and Homicide by People with Mental Illnes (NCISH)

  • National Confidential Enquiry into Patient Outcome and Death (NCEPOD) has widened its original remit looking at perioperative deaths to include near misses.

Disease surveillance

Collecting data on the incidence of some specific conditions relies on general practice consultations or hospital admissions. Asthma is a good example in which accurate diagnosis (case definition) and coding are important, and a universally agreed system of case definition and coding is very useful. For example, the International Classification of Diseases (ICD) classifies asthma into extrinsic, intrinsic, chronic obstructive, exercise induced, cough variant and unspecified, each with associated severity codes. Published in 1994, there is a need for revision and a new standard will be published in 2018. Specific notification or registration systems are in place for monitoring cancers, congenital anomalies and infectious diseases.

Cancer registration

Cancer registration is voluntary and undertaken by regional centres across the UK under strict policies set down by Public Health England (PHE) and the Health Research Authority . The national system tries to record information on every patient with a diagnosis of cancer. Categories include diagnosis, tumour stage, treatment, place of treatment, consultant and place of death. Data are published by PHE, giving direct and indirect measures of incidence, mortality and survival. Cancer registration data are also used for epidemiological research into healthcare outcomes.

Congenital anomalies notification

Notification of congenital anomalies is also voluntary. The National Congenital Anomaly System (NCAS) was closed in 2010 because of perceived under-reporting in comparison with other registries and was replaced by the British Isles Network of Congenital Anomaly Registers (BINOCAR), collating information about birth congenital anomaly prevalence and associated foetal, neonatal and perinatal mortality, in addition to prenatal diagnosis and any subsequent terminations of pregnancy. In 2015, it was transferred to PHE, underneath which sits the British and Irish Network of Congenital Anomaly Research Database (BINOCARD) .

Communicable disease surveillance

Notification of infectious diseases was first established in the UK in the late 19th century, when it was based on clinical suspicion and the reports of alert clinicians, with or without microbiological confirmation. Now there is a statutory requirement to notify certain infectious diseases ( Information box 7.4 ). The list of diseases changes over time.

Information box 7.4
Source: Public Health England.
Diseases notifiable (to Local Authority Proper Officers) under the Health Protection (Notification) Regulations 2010

  • Acute encephalitis

  • Acute infectious hepatitis

  • Acute meningitis

  • Acute poliomyelitis

  • Anthrax

  • Botulism

  • Brucellosis

  • Cholera

  • Diphtheria

  • Enteric fever (typhoid or paratyphoid)

  • Food poisoning

  • Haemolytic uraemic syndrome

  • Infectious bloody diarrhoea

  • Invasive group A streptococcal disease

  • Legionnaires' disease

  • Leprosy

  • Malaria

  • Measles

  • Meningococcal septicaemia

  • Mumps

  • Plague

  • Rabies

  • Rubella

  • SARS

  • Scarlet fever

  • Smallpox

  • Tetanus

  • Tuberculosis

  • Typhus

  • Viral haemorrhagic fever

  • Whooping cough

  • Yellow fever

The Communicable Disease Surveillance Centre (CDSC) of the Public Health Laboratory Service (PHLS), set up in 1977 before it became the Health Protection Agency (HPA), part of PHE, is now the PHE Centre of Infectious Disease Surveillance and Control , and is responsible for the administration of the notification system, working closely with public health agencies in the rest of the UK. Its functions are to undertake:

  • Surveillance of communicable diseases

  • Surveillance of immunisation and vaccination programmes

  • Investigation and control of communicable disease

  • Epidemiological research

  • Teaching and training in communicable disease epidemiology

Notification of infectious diseases

In the UK, communicable disease surveillance relies on notification of new cases by clinicians and on information from a network of microbiological laboratories which, since 1939, have been required to report to a national centre. A network of approximately 100 sentinel general practices return data on communicable and respiratory diseases to the Royal College of General Practitioners' (RCGP) Research and Surveillance Centre (RSC). The RSC publishes weekly and annual prevalence reports. The diagnoses are made clinically, without laboratory confirmation, using ‘diagnostic guidelines’ provided by the RCGP. These are not strict diagnostic criteria, but do represent an attempt to achieve some standardisation in the diagnoses. Important conditions include influenza-like illnesses and food- and water-borne conditions. The data are shared with the HPA and Department of Health ( Information box 7.5 ). Information on influenza in this context can be found on the PHE website ( https://www.gov.uk/guidance/sources-of-uk-flu-data-influenza-surveillance-in-the-uk ). The UK National Reference Laboratory for Food Microbiology, part of PHE, also collects data from official control laboratories.

Information box 7.5
Source: Royal College of General Practitioners (RCGP).
Communicable and respiratory diseases in England and Wales reported by the RCGP weekly returns service

Water- and food-borne disorders:

  • Infections intestinal disease

  • Viral hepatitis

  • Non-infective enteritis and colitis

Environmentally sensitive disorders

  • Asthma

  • Hay fever/allergic rhinitis

  • Respiratory and chest symptoms

  • Conjunctival disorders

Respiratory infections

  • Acute bronchitis

  • Common cold

  • Influenza-like illness

  • Acute laryngitis/tracheitis

  • Pleurisy

  • Pneumonia/pneumonitis

  • Respiratory system diseases

  • Acute sinusitis

  • Strep sore throat, scarlatina and peritonsillar abscess

  • Acute tonsillitis/pharyngitis

  • Upper respiratory tract infections

  • Whooping cough

  • Infectious mononucleosis

  • Lower respiratory tract infections

  • Acute otitis media

Vaccine sensitive disorders

  • Measles

  • Mumps

  • Rubella

Skin contagions

  • Bullous dermatoses

  • Chickenpox

  • Herpes simplex

  • Herpes zoster

  • Infections of skin and subcutaneous tissue

  • Scabies

  • Other skin and integumental tissue symptoms

  • Impetigo

  • Scarlatina

Nervous system disorders

  • Peripheral nervous system disorders

  • Meningitis/encephalitis

  • Nervous and musculoskeletal symptoms

Genitourinary system disorders

  • Urinary tract infection/cystitis

  • Sexually transmitted and other genital infections

Examining data from different sources

Putting data from different sources together can be very informative. For example, in the early 1980s in the UK, when the public health policy of rubella immunisation of 11-year-old schoolgirls had been in operation for about 12 years, the first cohort of immunised girls were having their first babies. However, notification of congenital rubella remained high, as did therapeutic abortions on the grounds of rubella in the first trimester. Rubella infection in the early stage of pregnancy results in foetal damage in approximately 90% of infants, and the lack of a major policy effect was disappointing. Immunisation of girls only, and not boys, had allowed the disease to continue to circulate. The partial immunisation of the population raises the average age at which the unvaccinated catch the disease, causing those women who had missed immunisation, or who were poorly protected, to remain vulnerable. With the introduction of the measles, mumps and rubella (MMR) vaccine in 1988, the policy was changed and MMR is now given to girls and boys at 12 and 47 months.

International infectious disease surveillance and information sources

Most developed countries have systems for reporting and monitoring communicable diseases. The WHO was established on 7 April 1948 by the United Nations. The objective was to enable all peoples of the world to attain the highest level of health – defined as a state of complete physical, mental and social well-being, and not merely the absence of disease or infirmity. The WHO vision is that every country should have the means to identify, verify and respond to epidemics and emerging infectious diseases as they arise, in order to minimise their impact on the health and economies of all nations. Globalisation, climate change, the growth of huge cities and the explosive increase in international travel are increasing the potential for rapid spread of infections.

Global infectious disease surveillance

The WHO Department of Communicable Disease Surveillance and Response (CSR), now called Global Alert and Response (GAR) , was set up in 2001 with three strategic aims: containing known risks, responding to the unexpected and improving preparedness.

GAR's core function is to:

  • Develop a global operational platform for communicable disease response and provide regional office support in the event of a major disease outbreak

  • Support states in their capacity to respond to epidemics in order to meet the requirements of the International Health Regulations (IHR) 2005, including provision of laboratory capacity, early disease warning and response

  • Support national and international training programmes for IHR

  • Support states in the preparation and response to pandemic and seasonal influenza and to develop standardised approaches for other major epidemic diseases such as meningitis, yellow fever and plague

  • Strengthen biosafety and biosecurity readiness for dangerous and emerging pathogen outbreaks, such as severe acute respiratory syndrome (SARS) and viral haemorrhagic fevers.

These strategic aims underpin all public health strategies for the surveillance, prevention and control of infectious diseases. IHR is the only global regulatory framework agreed on by the international community to support surveillance of global infections. Its website publishes health statistics on a wide variety of infectious diseases worldwide ( http://www.who.int/ihr ).

Special surveillance systems

The UK has a special surveillance system for acquired immune deficiency syndrome (AIDS). Genitourinary specialists, dermatologists and microbiologists supply confidential reports to PHE, which has developed the HIV and AIDS Reporting System (HARS). Similar surveillance and monitoring systems are in place across Europe and in North America.

Monitoring adverse reaction to drugs

A system for monitoring adverse reactions to medicines is in place in most countries. In the UK, a Yellow Card is used to report all suspected reactions to new medicines and serious suspected reactions to established medicines, even if the reaction is already well recognised or the causal association is uncertain. The system is administrated by the Medicines and Healthcare Products Regulatory Agency (MHRA) and PHE.

Measures for health of populations

Mortality and morbidity statistics are published by the WHO, and mortality statistics such as child (deaths in children under the age of 5 years) and infant (deaths under 1 year of age) mortality rates are used as measures of the health of nations, using comparisons between high-, medium- and low-income countries.

Mortality and life expectancy

The Office for National Statistics (ONS) in the UK regularly publishes mortality statistics that are used extensively for monitoring the health of populations. They are also used in resource allocation, in planning and monitoring services, and in describing and monitoring patterns of disease. For example, the number of deaths from AIDS and influenza epidemics is used to monitor the patterns of those conditions.

Mortality rates are often used as proxy measures for morbidity in the population, e.g. using deaths from suicide to monitor psychiatric morbidity and the effectiveness of health interventions on mental health. The appropriateness of the way measures of performance are chosen and applied is open to debate. Mortality statistics are derived from notification and civil registration of death, where the doctor performs the vital role of death certification. Accuracy and standardisation of case definitions are clearly essential.

Years of life lost refers to the number of years of life lost due to premature death, taking age 85 as the ‘cut-off’, and years of working life lost is the number of years of life lost if death occurs before the end of working life, taken as age 65. These statistics are useful in comparing mortality in different parts of the world and in evaluating the effectiveness of policy and service innovations (e.g. accident prevention, legislation for compulsory car seat belts).

Other official statistics relating to health outcomes include life expectancy, maternal and perinatal mortality, child and infant mortality, communicable disease surveillance, cancer registration, congenital abnormalities and abortion notifications.

Morbidity

True morbidity, in terms of incidence and prevalence, is often difficult to measure. Service activity, such as Hospital Episode Statistics (HES) , is sometimes used as another proxy measure for morbidity or to assess the need for services.

The population census and health surveys

General measures of health (and sickness) are obtained from the population census held to date every 10 years in the UK, and from a variety of health surveys. The General Household Survey (GHS) was an annual survey of a stratified random sample (see later) of households, carried out by the ONS since 1971 and last run in 2007. Its questions were included in the General Lifestyle Survey, which ended in 2012. Some of the information is covered as part of the ONS Integrated Household Survey (IHS) . The survey aims for a sample of 17 000–20 000 different households every year, and is intended as a continuous longitudinal survey which can detect trends. Financial constraints have meant that there are some years missing. A large range of questions are asked, covering health and sickness (including long-standing illness or disability, acute illness and general health), lifestyle and health behaviours. Additional questions have been included on mental health. The latest survey was published in 2015 and focused on questions about sexual health and cigarette smoking.

Some other health surveys have focused on specific conditions, such as cardiovascular disease. The annual Health Survey for England (HSE) was commissioned by the Department of Health and started in 1991, aiming to monitor progress on Health of the Nation targets in obesity and high blood pressure, but now has a different focus annually. Its most recent survey covered social care and collected information on children's physical activity. A large number of other surveys from the ONS cover a wide variety of health-associated topics, general practice, psychiatry and other subjects, such as the health of prisoners and health inequalities.

Measures for quality of life (QALYs)

With the aim of measuring health in terms of ‘quality of life’, a series of instruments for measuring socio-medical indicators of positive health and well-being have been developed. The Nottingham Health Profile was among the first and has been well validated.

Health inequalities

There are clear differences in health as measured by death rates, or incidence and prevalence for particular diseases. For example, there were 36.7 million people living with AIDS worldwide at the end of 2015. Of these, 1.8 million were children under 15 years old and approximately 2.1 million were newly infected in 2015. More than 50% of people living with AIDS are from eastern and southern Africa, with a further 6.5 million in West Africa, and these people bear an inordinate share of the global HIV burden ( Fig. 7.2 ) . Since global treatment targets were set in 2003, AIDS-related deaths have decreased by 43%. Although the number of people dying in sub-Saharan Africa declined by 32% between 2005 and 2011, this area still accounted for more than 70% of the deaths in 2015.

Fig. 7.2, Global variation in health outcomes:

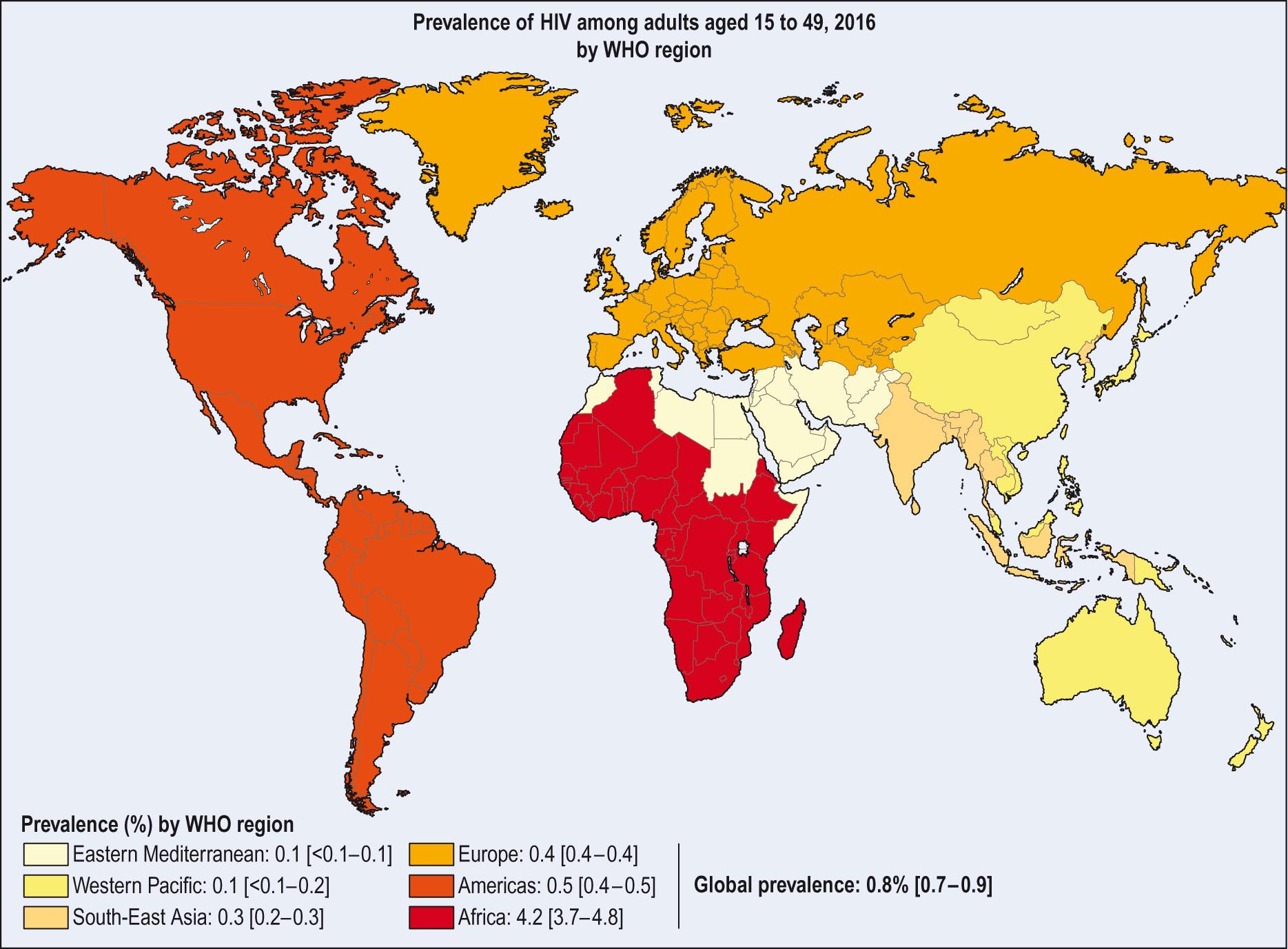
There are many factors that could contribute to this wide-ranging variation. As a general rule, consideration of the impact of social, economic, environmental and political influences, as well as access to medicines and medical services, on the health of populations gives an indication of how improvements might be achieved. Not all these factors are amenable to medical intervention.

Health inequalities in the UK

Since the passing of the New Poor Law Act in 1834 in the UK, there has been much interest in the patterns of health and disease, led by the General Register Office, which was founded in 1837. The Poor Law Commissioners commented on the ‘filthy, close and crowded’ housing, the ‘want of drainage’ and the ‘putrefying matter’ where the ‘industrious poor are obliged to take their abode’.

Socio-economic differentials in health still persist today, and the UK government launched a number of initiatives to reduce polarisation in society. The Social Exclusion Unit Report (2001) A New Commitment to Neighbourhood Renewal aimed to ensure that ‘within 10–20 years, no-one should be seriously disadvantaged by where they live’. Throughout the UK, strategies have been developed for the improvement of health, with the reduction on inequalities within different regions being an important integral part of the proposals: The NHS Plan for England, Toward a Healthier Scotland, Better Health Better Wales and, from Northern Ireland, Investing for Health.

The decennial supplement produced by the ONS, Geographic Variations in Health (2001), reviewed the position, looking at regional and social inequalities. The key findings are given in Information box 7.6 . Right Care is the UK NHS programme: intelligence, innovation and implementation, launched in 2010 to maximise:

  • The value that the patient derives from their own care and treatment

  • The value the whole population derives from the investment in their health care.

For example, through publishing the NHS Atlas Series, they aim to reveal variations in healthcare systems that can be used by commissioners to address inequalities.

Information box 7.6
Geographic Variations in Health , 2001 in the UK – key findings

  • Age-standardised mortality is higher in Scotland, Wales and Northern Ireland than in England

  • Within England, age-standardised mortality is higher in the north

  • Variation in health between local authorities within regions is greater than the variation between regions

  • High levels of area deprivation produce higher levels of mortality in relation to:

    • –

      Ischaemic heart disease

    • –

      Lung cancer

    • –

      Stroke

    • –

      Infant deaths and stillbirths

  • High levels of area deprivation produce increased incidence of:

    • –

      Lung cancer

    • –

      Teenage pregnancy

  • Social class differences make a larger contribution to male mortality variation than region of residence but the latter is still an important determinant of mortality among those in Social Class V

  • London has the highest rate of mortality from infectious and respiratory diseases

Changes in health outcomes over time

Although mortality rates are generally declining, reviewing the changes over time has shown that the areas where health is poorer show the lowest reduction in mortality. Certain areas stand out as relatively unchanged over many years. Examples are the high infant mortality in urban districts, such as Whitechapel in 1903 and in 1964, and similarly, the low levels of life expectancy in Manchester and Liverpool in 1911–1912 and in 1995–1997.

In 2009, the House of Commons Health Committee reported on health inequalities in the UK. Although they found that the health of all groups had improved over the previous 10 years, the gap between the social classes had also widened, by 4% in men and 11% in women, due to the greater health improvement seen amongst the rich. In 2017, PHE published a report which showed that little has changed. Those living in more deprived areas can expect to die some 7–9 years earlier than those in affluent areas and spend around 20 more years living in poor health than those living in more prosperous areas, evident in a geographical north–south divide.

Since 1950, deaths from heart disease, stroke and infectious diseases have all declined greatly. Not so cancer, which in 2015 was the most common cause of death in the UK. Whereas improvements in treatment have led to reductions in mortality for some cancers over the preceding 10 years, the incidence of some cancers appears to have increased considerably: in particular thyroid, liver, skin and kidney cancers in both sexes, small intestine cancer in males, and head and neck cancer in females ( Fig. 7.3 and Information box 7.7 ).

Fig. 7.3, Age-standardised rates of newly diagnosed cases and deaths from cancer in England between 1995 and 2015.

Information box 7.7
Key changes in cancer mortality and incidence 2000-2010

Key changes in cancer mortality 2000-2010

  • Mortality has decreased for approximately half of the most common cancers, including male lung, bowel, female breast and prostate cancers

  • Stomach cancer mortality has decreased by approximately 34% due to:

    • –

      Decline in Helicobacter pylori prevalence

    • –

      Increase in dietary fresh food

    • –

      Improvements in diagnosis

  • Cervical cancer mortality has decreased by 28% due to

    • –

      Screening

  • Prostate cancer mortality has decreased by 11% due to

    • –

      Screening with prostate-specific antigen (PSA) testing

    • –

      Better treatments

  • Liver cancer mortality has increased by approximately 36%

  • Digestive organ cancer mortality has increased by approximately 23%

  • Uterine cancer mortality has increased by approximately 14%

  • Malignant melanoma mortality has increased by 18% in males and 5% in females

Key changes in cancer incidence 2000-2010

  • Stomach cancer incidence has decreased by approximately 30%, for the same reasons as mortality has deceased

  • Lung and laryngeal cancer incidence in males has decreased by approximately 15% due to

    • –

      Reduced alcohol and tobacco use

    • –

      Reduced environmental exposure to tobacco smoke

  • Ovarian and oesophageal cancer incidence in females has decreased by approximately 10% due to

    • –

      In ovarian cancer, improved lifestyle, increased use of oral contraceptives and breastfeeding

    • –

      In oesophageal cancer, reduced alcohol and increased fruit and vegetable consumption

  • Malignant melanoma incidence has increased by 65% (males) and 40% (females) due to

    • –

      Increased recreational exposure to UV

    • –

      Increased surveillance and better diagnosis

  • Liver cancer incidence has increased by 44% (males) and 31% females) due to

    • –

      Liver cirrhosis from alcohol and viral infections

  • Kidney cancer incidence has increased by 26% (males) and 36% (females) due to

    • –

      Obesity

    • –

      Continuing cigarette smoking

  • Prostate cancer incidence has increased by 22% due to

    • –

      Increased rate of diagnosis due to PSA testing

  • Thyroid cancer incidence in females has increased by 67% due to

    • –

      Increased breast cancer incidence and subsequent treatment

  • Mesothelioma incidence in females has increased by 24% due to

    • –

      Secondary exposure through handling of asbestos-contaminated work clothes (the disease has an estimated 40-year latency and the incidence is expected to increase).

In 2012, cancer mortality in males in the UK was lower than in other European countries; mortality in females was higher, however. Lung cancer alone accounted for more than 20% of deaths and lung, bowel, breast and prostate cancers are responsible for almost half (46%) of all cancer deaths.

The National Strategy for Cancer (Improving Outcomes: A Strategy for Cancer) was published in 2011, with its aim of improving health outcomes for people with cancer. The main aims of the strategy are to:

  • Promote lifestyle changes to reduce cases of preventable cancers

  • Increase uptake of cancer screening and introduce new and effective screening programmes

  • Increase early diagnosis to improve the scope for successful treatment

  • Improve patient experience and support for cancer survivors

  • Ensure that all patients have the best possible treatment, case and support.

Interpretation of data

An important part of the study of epidemiology is the understanding and detection of bias (see later). For example, are the increases in incidence or mortality of certain cancers over time real, due to improved diagnosis, or the result of better cancer registration? Whereas births and deaths are collected by national registration and considered to be high-quality data, much else is of very poor or variable quality, including factors such as registration of cause of death, where there has been little regulation over the years.

Data inadequacies

The inadequacy, incompleteness and inaccuracy of much available data have already been referred to. For example, abortion statistics may be influenced by non-residents moving into temporary accommodation, or policy differences in different parts of the UK. Administrative boundary changes and postal code changes also produce problems of data interpretation over time. The latter is being improved with the use of map grid referencing.

Clustering

Clustering of risk factors in areas where health outcomes are poor may encourage the suggestion that one causes the other. The strong association, or collinearity , may in fact be due to clustering. Areas where health outcomes are poor are usually areas of multiple deprivation. Careful analysis of the data is required before one can conclude that specific deprivation might cause one or more of the poor outcomes. For example, sick people are more likely to be out of work and hence poorer than those who are well, so they may end up living in poor areas because of their ill health, rather than the reverse.

Socio-economic factors

It has been suggested that geographical differences in health are simply a reflection of a concentration of people of a lower socio-economic status. For example, large differences in infant mortality are seen between those with fathers in Social Class V compared with those with fathers in Social Class I. Mortality rates are also higher among men in Social Class V. In Africa, inequality and a lack of social cohesion, rather than relative poverty, are highly correlated with higher HIV prevalence.

Health-related behaviours

Epidemiologists are also interested in the contribution that health-related behaviour and the environment make to disease variation. Geographical variation in behaviour that affects health may produce different regional outcomes. Smoking is a good example, as areas with high incidence of lung cancer and high mortality correspond with areas of low social status, where individuals are also more likely to be smokers. Less clear is the influence of physical activity, which varies with social status and shows a north–south divide in England.

Healthcare facilities

The aim of the NHS, established in 1946, was to have healthcare facilities evenly spread throughout the population. In the 1970s, Tudor Hart saw that those most in need of health care were the least likely to receive it, and proposed the ‘inverse care law’ that led to the introduction in 1976 of formula resourcing. This should have made things equitable. Nevertheless, expansion of private services remains concentrated in the south of England and poverty and poor educational skills both reduce appropriate access. Although there is a policy of active shifting of resources to more deprived areas of the UK, this has not led to any closing of the gap and people within more deprived areas have significantly lower life and disability-free life expectations.

Environmental factors

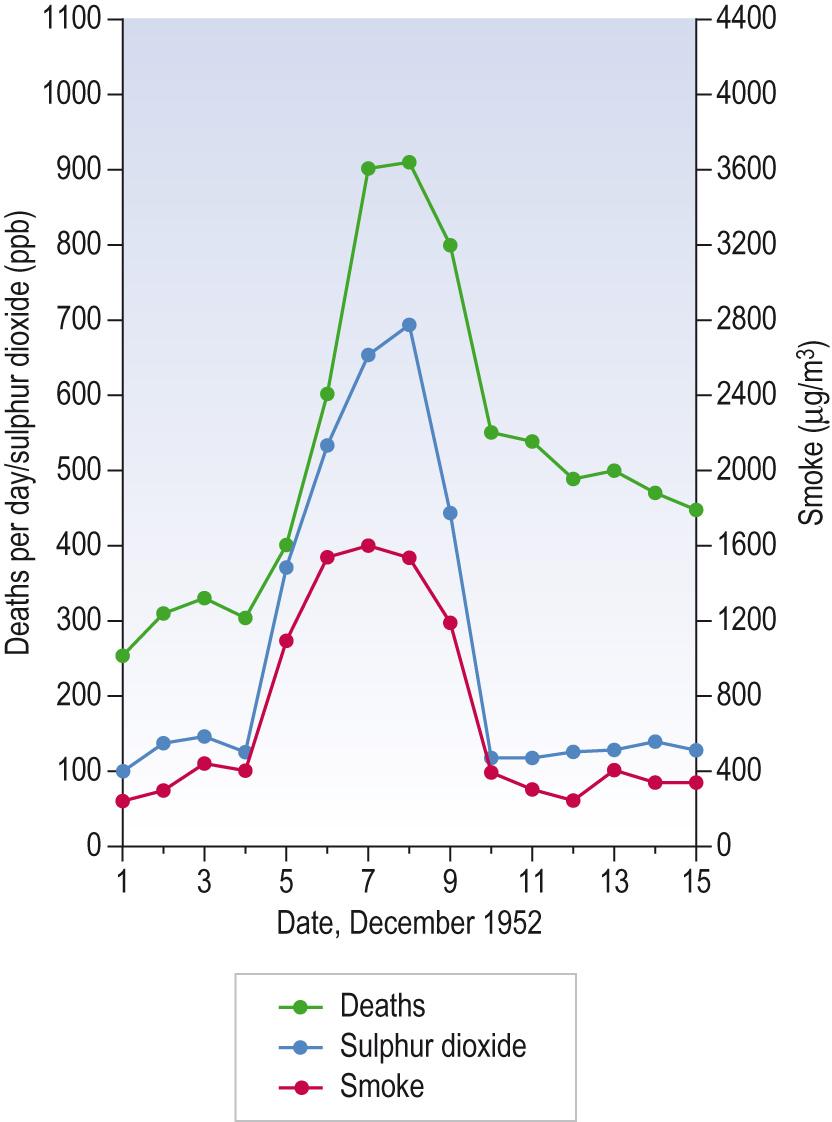
Environmental factors are also likely to produce different geographical patterns in, for example, the incidence of various congenital anomalies. Ischaemic heart disease has been shown to be correlated with rainfall, water hardness, temperature, manual employment and car ownership, but questions about the environmental contribution to disease have proved controversial as in, for example, the role of electric power lines in the incidence of leukaemia. In contrast, atmospheric pollution is strongly associated with excess mortality from respiratory disease. The industrialisation of Britain resulted in a major increase in air pollution, when smoke from coal burning mixed with mist and fog to produce smog, which then contributed to increased mortality and morbidity ( Fig. 7.4 ) . The introduction of the Congestion Charging Zone (CCZ) in London in 2003 seemed to offer a unique opportunity to assess potential improvements in health outcomes, with hypothesised significant reductions in air pollutants. However, the hoped-for reductions have not been achieved and any effect of the CCZ on pollutant levels has been confounded by other concurrent broader regional pollutant and weather changes, as well as increased use of diesel-powered vehicles.

Fig. 7.4, Deaths associated with pollution.

Migration

When health differences at a single point in time are considered, another effect that needs to be taken into account is that of migration ( Information box 7.8 ). A ‘healthy migrant effect’ has been observed: this occurs because younger people in good health and with, consequently, lower mortality rates, tend to move longer distances and into more affluent areas or countries. This can affect the average mortality rate of the area they move into. When migrants become ill, they may return home to die, and it is the place of death, not the place where they became ill, that is registered. Migration effects may obscure real health differences caused by locality and disadvantage. Migration may also influence birth rates and fertility.

Information box 7.8
Example of confusing factors in migration: confounding

Unless we have appropriate knowledge about our population make-up and the way it changes over time, our understanding can be confused. For example, in a study of native American Indians in 1988, a very strong negative association was seen between a particular genetic haplotype (Gm3; 5.13.14) and non-insulin-dependent diabetes. This might lead to speculation that absence of this haplotype is a risk factor for the disease; but in fact, although the haplotype is very common among the Caucasian population, it was rare among American Indians. Migrant populations (in this case the Caucasians) have mixed with the native population over time and once the genetic admixture is taken into account, the particular relationship between the Gm haplotype and not having diabetes disappears. What has happened in this example is a phenomenon known as confounding . The study does also illustrate, however, that there is likely to be another genetic component present in American Indians that increases their susceptibility to diabetes.

Genetic factors and international migration also probably play an important part in disease incidence, producing pockets of the inherited haemoglobinopathies in the UK, for example. International migration has had much to do with the increased prevalence of tuberculosis (TB). London houses the highest proportion of TB sufferers in the UK, with particularly high rates in Newham and Brent. The TB rates in those not born in the UK is about 10 times that of those born here.

Standardisation of rates

When comparing prevalence or incidence of death or diseases in populations from different communities, geographical areas or time periods, the results may be misleading, as differences in overall (crude) rates may be due to differences in the age and sex structure of the populations.

One way to account for the difference would be by comparing rates in age bands of, say, 10 years, but this is laborious and cumbersome, and does not give a summary rate. The more usual way is to standardise the rates for age and sex. This would be the rate for a population of a specific age and sex structure. It must be borne in mind that standardised rates are simply mathematical manipulations, undertaken to allow comparison, and the resultant numbers are not the same as the crude rates.

There are two ways of standardising rates – direct and indirect ( Information boxes 7.9 and 7.10 ). Both have the same objective – to get round the problem of different (age and/or sex) structures when comparing populations. Comparisons are normally made using a reference, or standard population.

Information box 7.9
An example of direct standardisation

The crude death rate for England and Wales in 1949 was 12.24 per 1000 and in 1979 was 12.41 per 1000. Is it possible that health advances have made no impact on the rate of death, or are differences in the population age structure over time giving a false impression? To examine this, we can use direct standardisation and calculate what the likely death rate would have been in 1949 (study population) if the population had the same age structure as that of 1979 (standard population). In other words, apply the rate in the study population to calculate the rate for the standard population. The age-standardised death rate for 1949, based on the 1979 population structure, can be calculated from the totals in Table 7.3 . Numbers in italics in the table are those calculated.

Age-standardised1949death=Expecteddeaths/populationin1000srateper1000=339868.4/23202×1000=14.65per1000

Thus, it seems that the death rate has fallen between 1949 (standardised at 14.65 deaths per 1000) and 1979 (actual 12.41 deaths per 1000).

Information box 7.10
An example of indirect standardisation

In 1988, 516 men were diagnosed with stomach cancer in Wales. Because Wales had a male population of 1.39 million at that time, the crude incidence rate of the disease in that region was 372 per million of the male population. We may wish to compare that figure with incidence in the whole of the UK. Table 7.4 shows how to estimate the expected incidence of stomach cancer in Wales, if Wales were experiencing the same incidence as the UK as a whole, i.e. applying the rate in the standard population to the rate in the study population.

The incidence we would expect in Wales, if Wales were experiencing the same rate as the whole UK, is 402 per million of the population. This can be directly compared with what has been observed.

Age-standardised=Observedrate/expectedrateincidenceratio=516/402.07=1.28
Standardisedmortalityratio=1.28×100=128

A ratio of 1.28 implies that the risk of stomach cancer in Welsh men is 1.28 times the risk in men in the UK in general. This could also be expressed as a 28% increase in risk.

Direct method of standardisation

This involves looking at the age-specific (death) rates in the study population and applying these rates to the same age groups in the standard population ( Information box 7.9 and Table 7.3 ). In our example, we could then calculate the number of deaths we would expect to see in England and Wales if the country was experiencing the same death rate as in the study populations. This number divided by the number of deaths actually seen in England and Wales (the standard population) multiplied by 100 is the comparative mortality index (CMI) . Results greater than 100 imply a higher death rate than expected in the study population than in the standard population.

Table 7.3
Death rate in 1949 if the population had the same age structure as in 1979
Age group (years) Deaths (1949) Population in 1000s (1949) Crude death rate per 1000 (1949) Population in 1000s (1979) Expected deaths
A B A/B C C × A/B
0–9 17 643 3417 5.16 3339 17229.2
10–19 2345 2869 0.82 4063 3331.7
20–29 5031 3339 1.51 3534 5336.3
30–39 6839 3189 2.14 3326 7117.6
40–49 16 062 3178 5.05 2020 10 201.0
50–59 32 097 2335 13.75 2924 40 205.0
60–69 60 580 1727 35.08 2257 79 175.6
70–79 77 127 957 80.59 1384 111536.6
80+ 42 218 228 185.17 355 65 735.4
Total 259 942 21 239 12.24 23 202 339 868.4

Indirect method of standardisation

This is slightly different from the direct method and takes the age-specific (death) rate of the standard population and applies it to the same age groups in the study population to calculate expected deaths. The ratio of observed deaths to expected, multiplied by 100, gives us the standardised mortality ratio (SMR) . Again, values above 100 imply the death rate in the study population is higher than the death rate in the standard population.

Table 7.5 shows that in 1971, the death rate was higher in Bournemouth than in the country as a whole. Bournemouth is a coastal resort in the south of England, which has a large elderly population, so it is not unreasonable to suppose that this may be the cause of the increased death rate. Only by adjusting the numbers in the table to take the different age structures into account can we make an attempt to answer the question (see Information box 7.10 and Table 7.4 ). In our example, we could calculate the number of deaths we would expect to see in Bournemouth if the people there were experiencing the national death rates for England and Wales in 1971. When we do this, we would expect to see 1664 deaths, but in fact only 1454 deaths actually occurred. This difference is expressed as the:

SMR=(numberofobserveddeaths/expectednumberofdeaths)×100=(1454/1664)×100=87.4

If the SMR were equal to 100 it would mean that the expected mortality rate in the study population was the same as the reference population. Because the SMR is less than 100, as it is in Bournemouth, this suggests that Bournemouth has a comparatively low mortality rate, even though the actual death rate is higher. The true association between death and living in Bournemouth has been confounded by the age structure of the population. The indirect method (SMR) is the one more commonly used when comparing mortality in different geographical areas.

Table 7.5
Is Bournemouth bad for your health?
Bournemouth England and Wales
Deaths per 1000 people in 1971 17.4 11.1
Standardised mortality ratio 1971 87.4 100

Table 7.4
Incidence of stomach cancer in Wales in 1988 if the incidence was the same as in UK as a whole
Age group (years) Incidence per million in reference population (UK) Population of Wales in millions Expected incidence per million
A B A × B
0–24 0 0.5 0
25–34 5 0.19 0.95
35–44 42 0.16 6.72
45–54 182 0.16 29.12
55–64 558 0.15 83.70
65–74 1478 0.11 162.58
75 + 2380 0.05 119.00
Total 402.07

Choice of method for standardisation

Why do we need both ways of standardising? Each has its advantages and disadvantages. If we wanted to compare the death rates in two study populations, one of which has an elderly population and the other a relatively young population, then it is best to take a ratio of the two CMIs obtained from the direct method. Ratios of SMRs can be misleading in this situation.

The direct method has a disadvantage when the study group is small because the numbers of people in the different age groups may be very small. Applying the death rates from these small groups to a large population can mean that a small change in the numbers of deaths in the study population can produce a large variation in calculated numbers of deaths from one year to the next. This increases the possibility of error in the measurement. For example, if in one year you were to observe just one death in 50 people in the 20- to 25-year age group, and in the next you observed two or three deaths in the same group, you might put that down to a chance finding and not be too concerned. But the increase is from a 2% death rate to 4% or 6%. Applying these proportions to a large population produces large differences in expected deaths, which may be very misleading. Using the indirect method is better, because we apply the death rate in the standard large population to the smaller study population.

Sometimes it is just not possible to use the direct method. In our example, we would need to know not only the number of people who had died in Bournemouth, but also the number of people who had died within each of the age groups that we used for the standardisation. This sort of information is generally available for the standard (UK) population but is more difficult to find easily or collect for a small study population.

The SMR can be calculated for all causes of death, a specific cause (e.g. cancers), a particular age (e.g. >65) or an occupational group. A similar principle can be applied to activities such as hospital admissions, in which case the index becomes a standardised admission ratio (SAR).

Epidemiological Enquiry

To understand the natural history, some possible causes of diseases and the effectiveness of treatments, specific studies are undertaken. A variety of methods are used, each selected to answer a specific research question. Understanding the principles underlying the epidemiological approach not only enables a critical appraisal of research evidence, as when reading research papers in medical journals, but also helps towards understanding research methods.

Some basic concepts in epidemiology

Some basic concepts used in epidemiology have already been discussed, e.g. incidence and prevalence, standardised mortality and morbidity rates. Other important basic concepts concern the distribution of data collected for epidemiological enquiry and statistical methods employed for analysing the data. The meaning of basic concepts rather than the mathematical calculations will be discussed.

The distribution of data

The distribution of actual data can be represented by a histogram . Distributions can be symmetrical, e.g. height, where the tails of the distribution are symmetrical ( Fig. 7.5A ) . Some distributions are asymmetrical, where there are more instances of extreme values at either small values (negative skew) or high values (positive skew) (see Fig. 7.5B ). Adult weight is positively skewed, in that the proportion of very heavy people is greater and further away from the most common value than is the proportion of very thin (light) people. Gestational age is negatively skewed, most babies being born at 39 or 40 weeks, very few born after 42 weeks, but a high proportion born before 36 weeks. Most distributions are unimodal in that they have only one peak, but Fig. 7.5C is bimodal (two peaks) such as, for example, the distribution of age of onset of Kaposi sarcoma in males with and without AIDS. Only very rarely are distributions U shaped: they are actually bimodal balanced distributions but with most measurements being at the extremes and few observations in the centre of the distribution.

Fig. 7.5, Data distributions and measures of centre.

The normal or Gaussian distribution curve

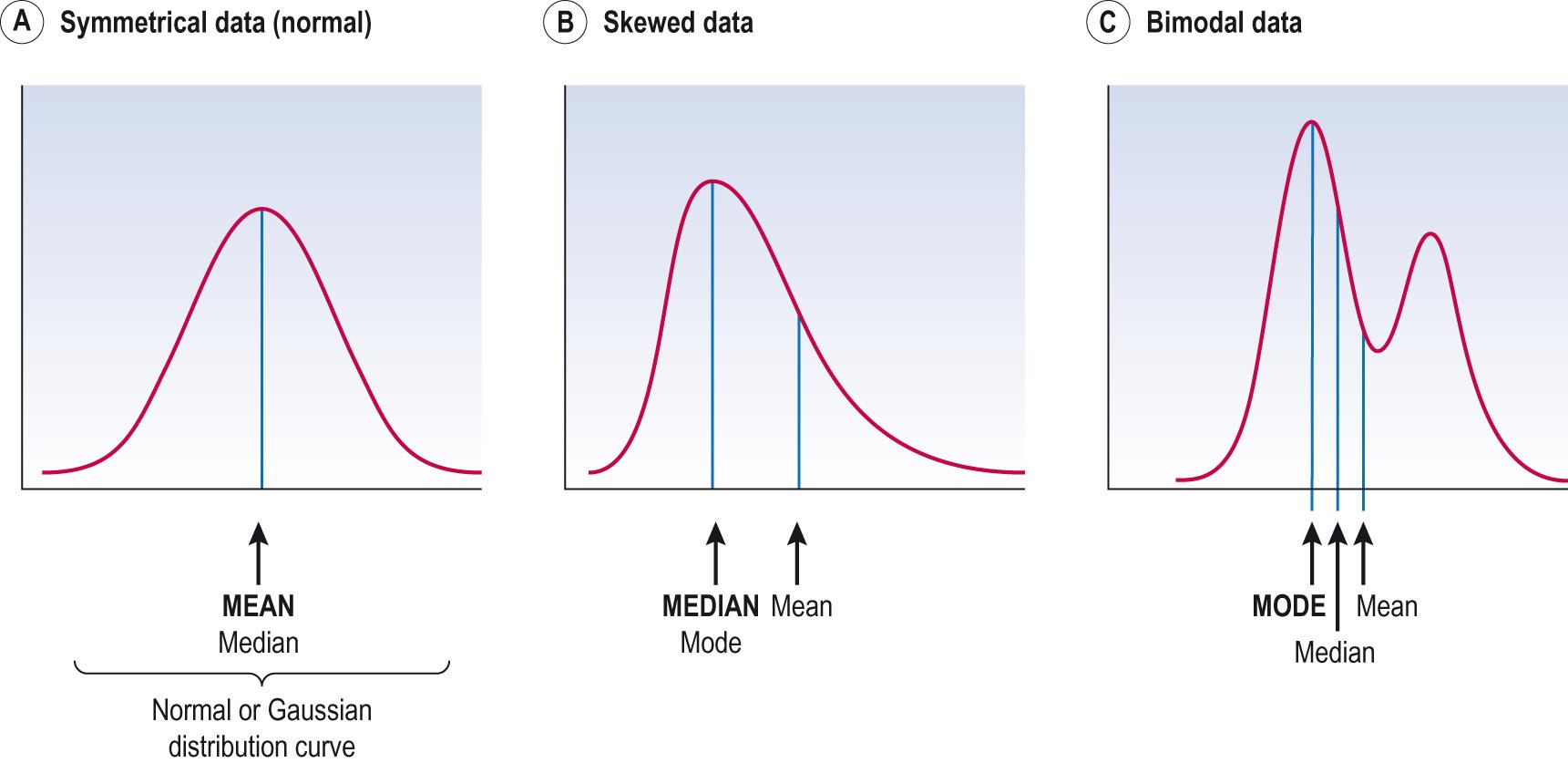
Frequency distributions can be thought of as smoothed curves through the appropriate large sample histogram. The Gaussian (or normal) distribution curve is bell shaped, symmetrical and with certain fixed properties. Its shape is uniquely defined by the mean and standard deviation (SD) of the data. Fig. 7.5A is an example of a Gaussian distribution, and adult height is very close to a Gaussian distribution. Much of theoretical statistics is based on the properties of the Gaussian distribution.

Some numerical data vary continuously, such as the height and weight of growing children, and are known as continuous variables . Other numerical data are discontinuous , such as the numbers of people in defined populations. The numbers of people are variable but differ at different points in time.

Measures of centre

In describing data, the concept of ‘average’, or centre , is important. Commonly used to mean ‘normal’, ‘regular’ or ‘middling’ for statistical purposes; ‘average’ needs to be more precisely defined. There are three main measures of average that are useful: the mean , the median and the mode . The best one to use in describing the data will depend on the shape of the data. In making the choice of which measure to use, it is very important to look at the data graphically. Because the mean is better than median (because it is a summary of a greater amount of information), and median is better than mode for statistical analysis, medians tend to be used only for quite skewed data, whereas mode would be restricted to bimodal or other oddly shaped distributions.

The mean

The mean of the data, sometimes called the arithmetic mean, is what we normally think of when we say ‘average’. The mean of a set of values is found by adding up all of them and dividing by the total number in the set. The mean is best used for data that are unimodal and not strongly skewed (see Fig. 7.5A ).

The median

The median is the value that lies in the middle of a set of values, once they are put in order (see Fig. 7.5B ). For example, if we have five babies with the following birth weights:

  • 3100 g, 3300 g, 3100 g, 3200 g and 3800 g

  • The order would be: 3100, 3100, 3200, 3300, 3800 g

  • Thus 3200 g would be the middle value, or median.

The median is slightly less obvious if there is an even number in the set. For example, if the set of birth weights were:

  • 3100, 3100, 3200, 3300, 3300, 3800 g

There are two middle values, 3200 and 3300. In this case the arithmetic mean of the two middle numbers is calculated to give the median of 3250 g.

The median is sometimes also referred to as the 50th percentile because half the data will lie at or below it and half at or above. This concept will be familiar when using children's growth charts, or centile charts.

The median is best used for data that has a substantial skew, or for data where the measurements are ordered (ordinal data) rather than arithmetical (e.g. pain scores). In this type of data, the difference between adjacent categories is not usually the same (e.g. the difference between mild and moderate is almost certainly not the same as between moderate and severe).

The mode

The mode represents the observation that is the most frequent. In Fig. 7.5C , there are two peaks, and the mode is the higher peak. In this case, however, the distribution would be better described as bimodal and it would not be appropriate to simply report the first peak. The mode is often used when dealing with data that are in categories and cannot be put into an order (categorical data) . For example, among the four blood groups O, A, B and AB, blood group A is the modal category in London because it occurs more frequently in this population.

Data from surveys about attitudes often use what is known as the Likert scale , which is a three- to five-point scale of responses that range from ‘strongly disagree’ to ‘no idea’ to ‘strongly agree.’ Medians can be used with these type of data as they are ordinal (ranked and ordered); if the data can be sensibly aggregated, means are sometimes used.

Measures of spread: standard deviation from the mean

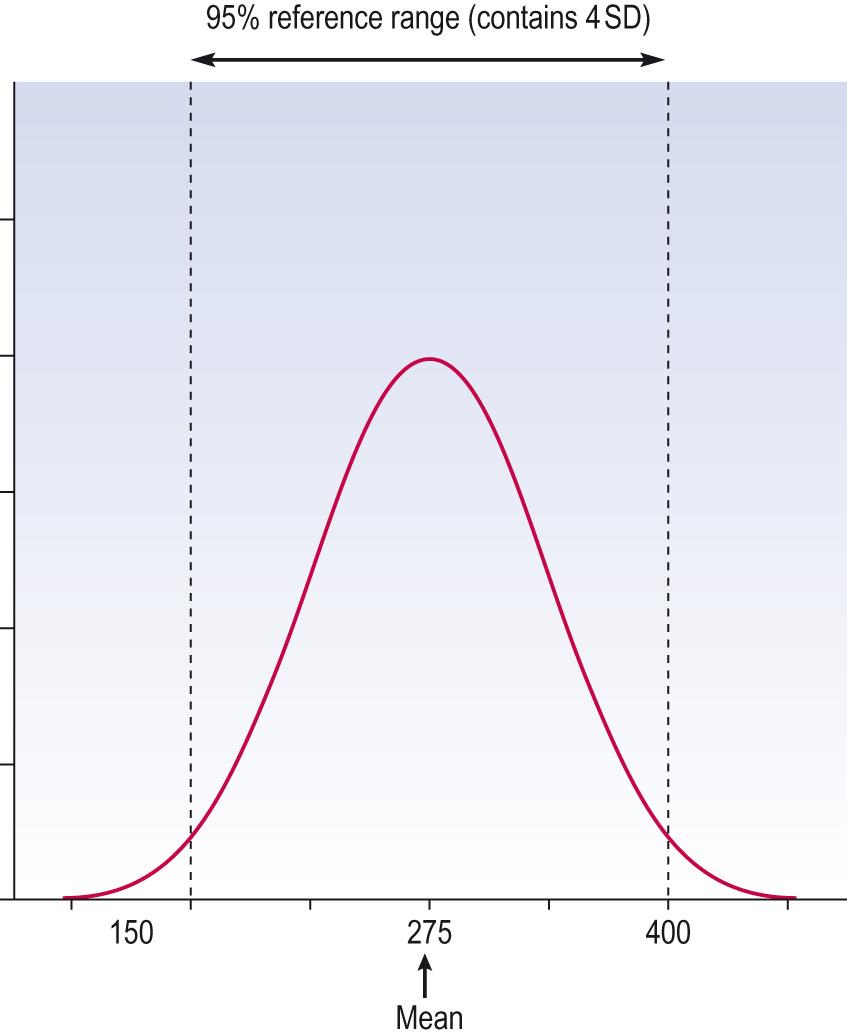
In describing data, if the distribution is symmetrical enough to be described by the mean then it is appropriate to describe the variability – a measure of spread of data from the mean – by the standard deviation (SD). The SD is arrived at using a formula (which it is not necessary to describe here, especially as every scientific calculator has a key to provide that number when a set of data are entered). Where data are normal (Gaussian), 95% of the data will lie between the mean ± 1.96 times the SD. For practical purpose we can usually assume that for data that are approximately Gaussian, about 95% will lie within the mean ± 2 SD. This is often the range that is considered ‘normal’ in clinical medicine, i.e. not of concern or not unusual ( Information box 7.11 , Fig. 7.6 ).

Information box 7.11
Standard deviation (SD) of normal platelet counts

The normal range for blood platelet count is 150–400 × 10 9 /L. A useful property of the normal distribution is that about 95% of observations lie within the range, mean ± 2 SD. (Actually, it is 1.96 SD but we are using 2 here because it is very close and simple to calculate). This range is known as the 95% reference range ( Fig. 7.6 ) . To produce this range, we take a sample that is representative of the population and use that to provide our assessment of mean and SD.

Fig. 7.6, Distribution of all platelet counts in a normal population.

Outliers

Sometimes an isolated value will stand out from the rest of the data set. This is known as an outlier, and checks are needed to see whether this is a mistake in measurement or transcription, or even consistent with life. If certainly wrong it can be excluded, but if it is real or unexplained then other methods of dealing with the data may be required, particularly if the data set is small.

Ordered data and the interquartile range

Some data do not follow a normal distribution and so an SD (although it can be computed) is not appropriate. Instead the data can be described in terms of percentiles, or percentage points. Paediatric weight growth charts are examples of skewed data ( Fig. 7.7 ) , Paediatric height growth charts are presented in the same way but the data are more normally distributed at the different ages.

Fig. 7.7, Growth centile chart for girls, showing weights for girls aged up to 19 years of age.

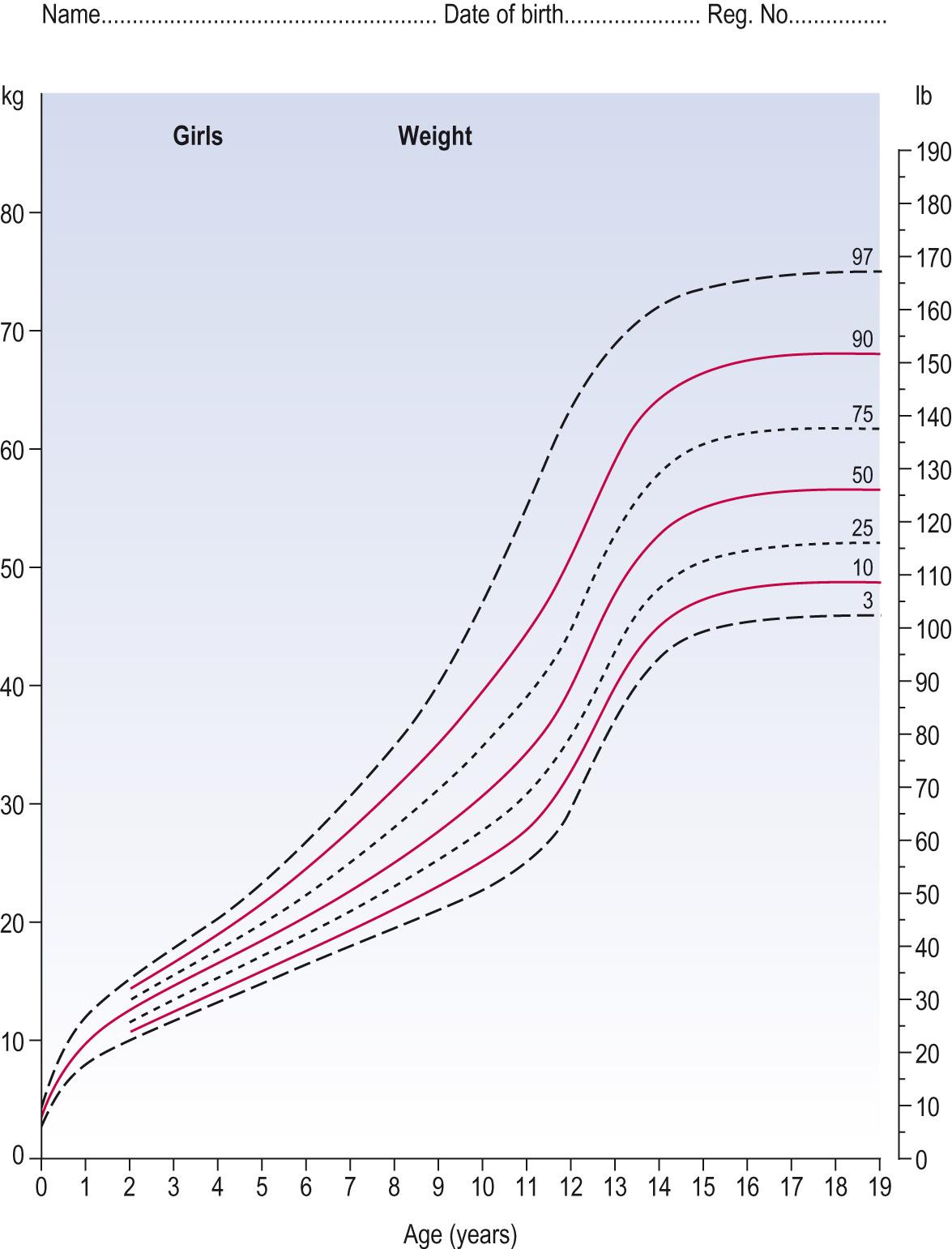
Various measures of spread such as the interquartile range or the interdecile range can be calculated from data. A box and whisker plot is a useful way of illustrating the data distribution ( Fig. 7.8 ) . The diagram provides a simple way of describing the data in some detail. It can be seen in the figure that there is a wide range of gestational ages at the lower end, with 50% of gestational ages ranging between 32 and 40 weeks, whereas at the top end the data are very tight, with 50% of gestational ages being between 40 and 41 weeks, showing a very skewed distribution.

Fig. 7.8, Box and whisker plot of gestational age at birth.

How accurate is the distribution summary?

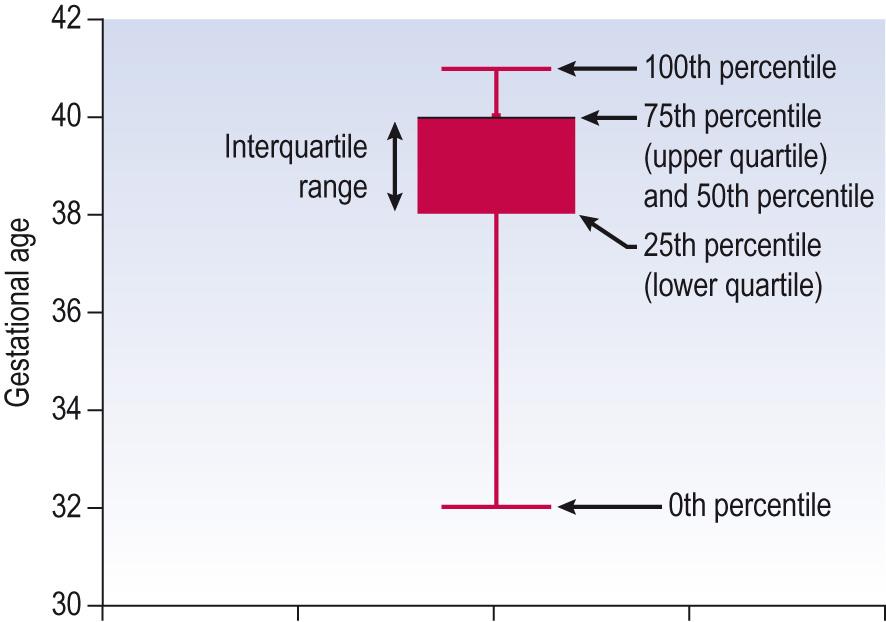
Measurements in epidemiology are usually taken from samples of the population, as it would be too difficult to take measurements from the whole population. But even when the whole population is measured, we are often interested in how representative it is of an unknown underlying rate. An estimated mean from one sample is unlikely to be the true mean in the population. However, if we could take an infinite number of random samples of the same size from the population, the distribution of the potential sample means will be normal or Gaussian, with a mean more representative of the true mean, provided that the sample size is not too small for distributions that are not Gaussian. The SD of the distribution of potential sample means is the standard error (SE) of the mean (SEM). The SE represents the uncertainty in the sample mean as a representative of the true mean ( Fig. 7.9 ) .

Fig. 7.9, The sampling distribution of mean platelet counts in a normal population.

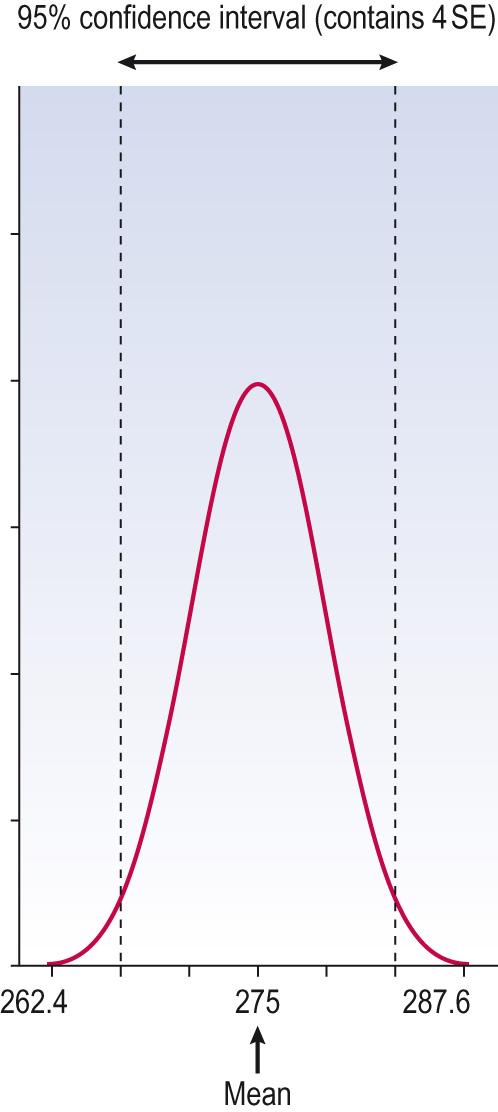
Whereas in clinical medicine we may be interested in an individual measurement, in epidemiology we are often more concerned with the true; i.e. population or underlying mean. We can never find the true mean because people are dying and being born every second, so we have to find a way of estimating where the true mean might lie. We could take the means of a number of samples of data, thus creating a set of means, and calculate the mean and standard deviation (the SE) of the means. However, it is possible to estimate the SE from one sample and from that infer the range in which the true mean is likely to lie.

Because the distribution of all potential sample means of given size is normal with an SD equal to the SE, 95% of all sample means will lie within the true mean ± 1.96 × SE. The one sample mean that we have calculated is within the true mean ± 1.96 × SE with 95% probability; hence the sample mean ± 1.96 SE will include the true mean with 95% probability. The sample mean ± 1.96 SE is referred to as the 95% confidence interval ( Information box 7.12 ) of the mean.

Information box 7.12
Calculating confidence intervals

Confidence intervals are calculated from the standard error (SE). The formula for estimating the standard error from one sample is:

, where n is the number of observations.

The 95% confidence interval, the parameters (limits) of the range of means in which the true mean lies, is the sample mean ± two standard errors (rounding up 1.96 to 2).

For example, if the sample we took to find the normal range of platelet counts consisted of 100 people, with a mean of 275 and standard deviation (SD) of 63, then we can calculate the SE and 95% confidence interval as follows:

SE=63√100=6.395%CI=275±2×6.3=262.4to287.6.

Standard errors and hence confidence intervals can be calculated for most summary measures including difference in means, proportions, differences in relative risks, odds ratios (OR) and SMRs.

Differences in non-symmetrical distributions are often better described by mean differences and 95% confidence intervals of mean differences rather than differences in medians. For example, it is more sensible to describe gestational age by median and percentiles, but if describing the difference in gestational age for babies born alive between 1970 and 2000, it would be better to describe this by a mean difference in gestational age.

You're Reading a Preview

Become a Clinical Tree membership for Full access and enjoy Unlimited articles

Become membership

If you are a member. Log in here

Related Posts