Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Hypertrophic cardiomyopathy (HCM) is a common yet challenging genetic heart disease with a prevalence of 1 in 500 people. It is characterized by an unexplained thickened heart muscle. It is a major cause of sudden cardiac death (SCD) in young adults, but most patients remain asymptomatic with a normal life expectancy. Because of the heterogeneous clinical course of the disease, the identification of at-risk patients is a clinical priority because implantable cardioverter defibrillators (ICDs) could successfully treat the ventricular arrhythmias that can trigger SCD. The use of ICDs has confirmed that ventricular arrhythmias are the precipitating mechanism in SCD.
HCM hearts have structural changes such as hypertrophy, myocyte disarray, and fibrosis, in addition to ion channel dysfunction that can create an unstable electrical milieu, predisposing the patient to arrhythmia. These abnormalities may alter the electrical activation, contraction, repolarization, and relaxation; in turn, this can affect the electrocardiogram (ECG), which records the cardiac electrical activity on the body surface. Various types of ECG abnormalities have been reported in HCM, such as pathologic Q waves, wide QRS, prolonged QT interval, and inverted T waves, , but these biomarkers are not specific to at-risk patients. These discrete, clinically interpreted ECG features, visually extracted from paper ECGs, do not objectively capture the shape diversity of ECG complexes.
Despite its biophysical underpinning, the ECG does not yet feature in current risk assessments for HCM. The European Society of Cardiology (ESC) HCM risk-SCD calculator includes seven clinical factors: age, family history of HCM-related SCD, unexplained collapse, maximum left ventricular (LV) wall thickness, nonsustained ventricular tachycardia (if sustained, it could be fatal), increased left atrial size, and maximum LV outflow tract gradient. This calculator, however, may overestimate risk and lead to inappropriate ICD implantation in some patients. Risk may also be underestimated in other patients because SCD can occur in low-risk patients.
The validation of new methods for risk stratification remains a challenge because of the low number of adverse events in HCM. Indeed, despite being a major cause of cardiac mortality in young adults, the incidence of SCD in HCM is less than 1% per year, which prevents its use as an endpoint in most studies. Clinical risk factors and the HCM risk-SCD calculator are recommended by the American College of Cardiology (ACC)/American Heart Association (AHA) and ESC guidelines, respectively. HCM risk stratification may therefore be improved through further characterization of the ECG, such as by using novel computational analysis techniques such as the ones proposed here. ,
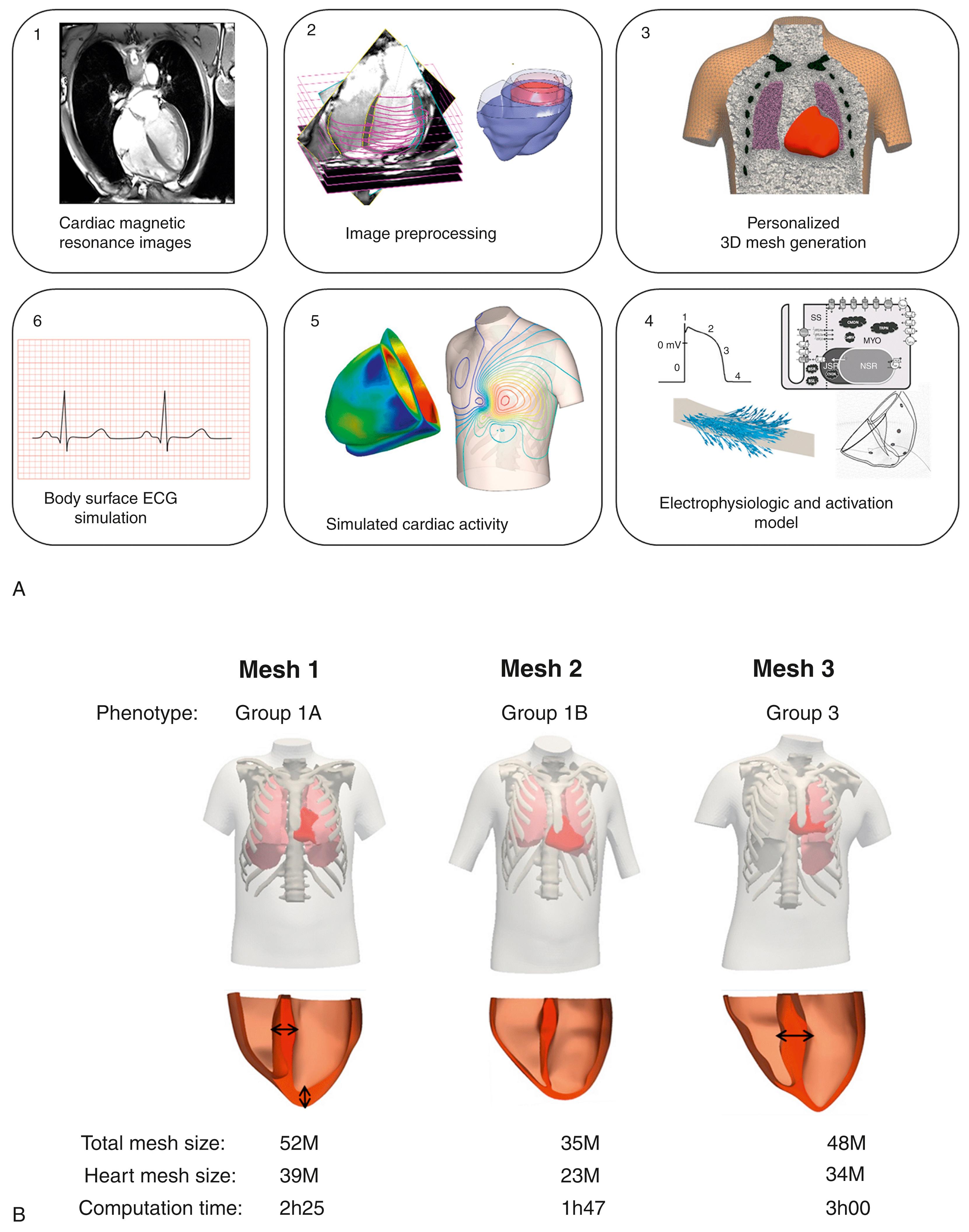
Computational techniques have emerged as powerful tools to analyze biologic and medical data thanks to their ability to handle large and heterogeneous data sets. Machine learning techniques have, for instance, been widely developed for classification and clustering of ECG signals, , from heartbeat classification , to automated patient diagnosis. Similarly, computer modeling and simulation frameworks have been developed and have provided useful insight into cardiac mechanisms from the level of the cell to the whole organ. They allow the personalized simulation of cardiac activity based on cardiac magnetic resonance (CMR) images. The combination of detailed imaging modalities, such as diffusion tensor imaging (DTI), with computer modeling has also enabled us to explain the relationships between the structure of the heart and cardiac function, which are challenging to investigate in vivo. Computational techniques such as machine learning and computer modeling therefore provide a set of methods that can help make sense of multivariate complex data sets and detect differences that might be challenging for the human eye. ,
The ECG signal provides a noninvasive representation of the cardiac activity, and its analysis can lead to diagnosis of cardiac disorders. To this end, signal processing and computational techniques allow for the extraction of biomarkers (features describing the ECG), such as time-interval biomarkers, which characterize the temporal dynamics of the electrical propagation during a cardiac cycle, and morphologic biomarkers, which quantify the shape of ECG waveforms, such as amplitude, width, and overall morphology. , Therefore, by developing computational approaches to analyze and simulate medical data, we can find answers to key questions of arrhythmia research and, in the context of HCM, understand its phenotypic heterogeneity and accelerate improvements in individual patient management.
This chapter describes how the development of computational methods for the analysis and interpretation of electrophysiologic clinical data can help investigate the diversity of HCM phenotypes with the ultimate aim of improving risk stratification in HCM. , As previously mentioned, HCM is a major cause of SCD in young adults, but most patients remain asymptomatic, and reliable methods for differentiating who will remain healthy with HCM from who will be devastated by disease complications are lacking. A novel approach of combining clustering, mathematical modeling, and computer simulations can address this challenge. This work is based on the hypothesis that both HCM structural and electrophysiologic abnormalities affect the activation and repolarization phase of the cardiac cycle, resulting in electrophysiologic abnormalities on the ECG with different degrees of severity in different patient groups.
Ultimately, the overall goal can be divided into two specific research questions: (1) Can we identify distinct phenotypes in HCM associated with different arrhythmic risk levels based on the ECG alone? (2) What are the HCM structural and electrophysiologic abnormalities that can explain these distinct ECG phenotypes?
The first question is addressed using mathematical modeling and computational clustering, based on morphologic QRS and T wave biomarkers, to identify distinct ECG phenotypes and compare them in terms of clinical markers and markers of arrhythmic risk. CMR-based torso-biventricular modeling and simulations help address the second question by evaluating the effects of structural and electrophysiologic changes on electrical propagation and the ECG to investigate the mechanisms that may explain the ECG abnormalities observed in the different phenotypes identified in the first research question. The methodology pipelines developed to identify and explain HCM phenotypes are summarized in Figs. 34.1 and 34.2 .
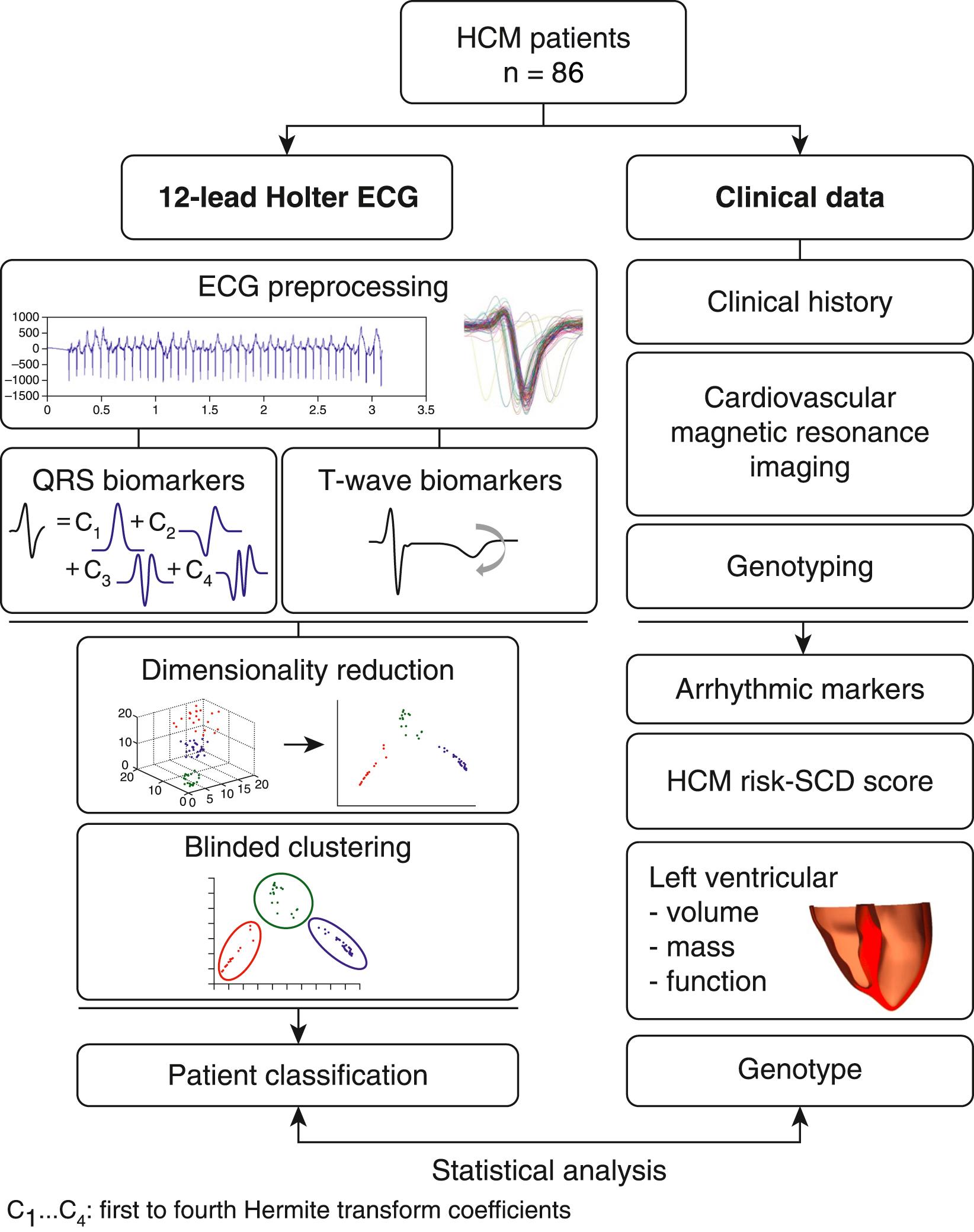
A total of 86 HCM patients were recruited from the University of Oxford Inherited Cardiac Conditions Clinic at the John Radcliffe Hospital in Oxford, United Kingdom. Diagnosis of HCM was made by the presence of a pathogenic genetic mutation; in the absence of an identified mutation, HCM was defined as LV hypertrophy (LVH; at least 15 mm) not originating from another cause. Patients were excluded if they had a diagnosis of coronary artery disease, diabetes, hypertension, or atrial fibrillation or an ICD with paced rhythm. Thirty-eight normal controls, who were nonsmokers without cardiovascular disease, hypertension, or diabetes, and who had no family history of cardiomyopathy or SCD, were also recruited. All participants underwent 12-lead ambulatory Holter monitoring (at a sampling frequency of 1 kHz, H12+, Mortara Instrument) for 24 hours. Standard 12-lead resting ECGs were also acquired from a Burdick 8500 digital electrocardiograph with the Glasgow algorithm. LV volume, mass, and function were obtained by CMR imaging, performed on a 3.0 tesla Trio MR system (Siemens Healthcare). The extent and morphology of hypertrophy were identified on short-axis images and categorized into four subtypes:
No hypertrophy: genotype-positive patients with wall thickness of 12 mm or less (G+LVH–)
Septal hypertrophy: basal and/or mid-septal wall thickness greater than 12 mm in genotype positive patients or at least 15 mm in genotype-negative patients
Apical hypertrophy: apical wall thickness at least 15 mm below papillary muscle level
Mixed hypertrophy: coexisting hypertrophy in septal and apical segments
Clinical assessments of HCM patients included history, physical examination, family pedigree, ambulatory three-lead Holter ECG, and echocardiography. Five conventional risk factors were considered: nonsustained ventricular tachycardia (NSVT; three or more consecutive ventricular beats at a rate of at least 120 beats/min lasting less than 30 seconds on clinical three-lead 24- to 48-hour Holter monitoring), unexplained syncope (at least one episode of unexplained syncope), family history of SCD (history of SCD in at least one first-degree relative 40 years old or younger or SCD in a first-degree relative with confirmed HCM at any age), massive LVH (LV wall thickness in any myocardial segment of at least 30 mm on short-axis CMR images), and abnormal exercise blood pressure (BP) response (rise in systolic BP less than 20 mm Hg or a fall of greater than 10 mm Hg from baseline to peak exercise in patients 40 years old or younger). The HCM risk-SCD score (2014 ESC guidelines) was calculated for each patient using seven disease variables as in O’Mahony et al. A risk score of at least 6% is classified as high risk and ICD implantation is recommended, 4% to 6% is intermediate risk and ICD may be considered, and less than 4% is low risk.
The raw digitalized Holter ECGs acquired required preprocessing to remove artifacts caused by muscular noise, respiration, and normal postural changes carried out during normal activities. The first 30-minute excerpts (around 2000 beats) from the Holter ECGs were used to analyze the eight linearly independent leads (I, II, V 1 –V 6 ) with custom-built software using MATLAB (Mathworks). A sensitivity analysis showed that analyzing different 30-minute excerpts in the recording yielded the same results. Thirty minutes also provided enough data to screen the excerpts and avoid changes in beat morphology caused by changes in heart rate, and the segments were manually checked to ensure an average heart rate of 70 beats/min.
A wavelet-based delineator extracted the peaks and boundaries of the ECG waveforms. The wavelet transform of a signal x(t) was defined as its decomposition according to a base of functions derived from an initial wavelet:
with
being the initial wavelet, a a scale coefficient controlling the width of the basis, and b a translation coefficient. The coefficients a and b can be chosen to be discrete: a = 2 k , k∈N.
The idea of this algorithm is that the frequency bands of the different ECG waveforms lie at different scales. For instance, the energy of the ECG is located between the scales 2 1 and 2 5 . The energy of the QRS is very low for scales higher than 2 4 , whereas T and P waves still have consequent energies at scale 2 5 . By representing these waveforms at different scales, the algorithm can perform the wavelet transform of the signal and reduce the delineation problem to simpler tasks, such as zero crossing or local optima detection. This is made possible using the derivative nature of the wavelet basis. Indeed, a zero crossing in the wavelet transform corresponds to a maximum or minimum in the initial signal, highlighting the waveform evaluated. The algorithm first detects the QRS complex, then identifies the waves of the QRS, then determines the QRS beginning points and endpoints, and finally detects the T and P waves.
High-frequency noise was removed using a low-pass Butterworth filter with a cut-off frequency of 45 Hz for QRS complexes and 25 Hz for T waves to allow the waveforms of interest. The magnitude of the frequency response (gain [G]) of a low-pass Butterworth filter was given as:
where w is the angular frequency, G 0 is the DC gain (gain at zero frequency), w c is the cut-off frequency (45 Hz), and n is the order of the filter ( n = 11).
This step enabled us to smooth the signal to remove notches or peaks caused by noise, which could otherwise lead to a misinterpretation of the morphology of the signal. Baseline drift was removed by a cubic spline method to avoid morphologic changes of noncardiac origin. The cubic spline method is based on the approximation of the baseline using knots to indicate the isoelectric level between the P wave and the QRS complex. Here, the knots were chosen 80 ms before the fiducial point of the QRS, on the PR segment. A first-order polynomial fitting would not represent the isoelectric line accurately because lines would connect the knots. Increasing the order of the polynomial, however, may lead to a risk for overfitting and increase of computational complexity. For cubic spline estimation, a third-order polynomial was used. The polynomial fitting takes its root in Taylor series expansion. Indeed, by defining the knots as {t i, i = 0,1,…} the baseline was computed using a Taylor series:
This formula can be truncated at the order of the polynomial (three in our case) and after different approximations over the derivatives, the baseline was estimated and then removed from the initial ECG. In addition, a notch filter rejected the 50 Hz main power artifact coming from the recording devices.
The first 20 beats with maximal ST segment‒T wave (ST-T) signal-to-noise ratio were considered for analysis and were aligned with respect to the QRS complex using Woody’s method. The signal-to-noise ratio was defined as the ratio between the ST-T peak to peak amplitude and the root mean square value of the background noise greater than 20 Hz. The alignment technique was based on the computation of the correlation between each beat and a template beat. The template beat was computed once, at the beginning of the segmentation, as an average of the first 20 beats as mentioned. No particular filtering or denoising method was applied because the only relevant parameter is the beat time position. The computation of the correlation between each beat and the template led to a lag matrix composed of the possible time differences and the correlation they achieved. A lag window of [–90,90] was defined to explore all the possible shifting of the curves and the corresponding correlations. The lag number achieving the maximum correlation between the two curves, computed by maximum likelihood estimation, was stored and the beat was shifted to this position to ensure alignment. This technique was repeated over all the beats until the maximum correlation was achieved for all. A window of 180 ms centered on the mean energy of the QRS and a 500 ms window aligned to the ST-T onset were computed in all eight leads per participant. ECG excerpts were checked to ensure there was the same heart rate in the segment and avoid misalignment from the ST-T onset because of changes in heart rate. Average QRS and ST-T waveforms were then computed.
From this preprocessed ECG signal, biomarkers from the QRS complex and the ST-T segment were computed. All biomarkers were calculated per lead from the average QRS waveform. Five standard QRS biomarkers were defined as follows, based on standard QRS measures and visual inspection of the ECGs:
QRS amplitude was defined as the absolute value of the difference between maximum and minimum of the QRS complex values.
QRS width was defined as the time interval between the QRS onset and the QRS offset.
The maximum ascending/descending or descending/ascending slopes of the QRS were defined as the first ascending and descending slopes, depending on the QRS complex pattern.
The percentage of negative time samples in the QRS were measured with respect to the isoelectric level (mostly representing the percentage of negative S waves with respect to QRS duration).
The QRS morphology (shape) was also quantified using mathematical modeling based on a combination of orthogonal Hermite functions, with a well-established ability to provide a compact representation of the QRS complex and denoise the signal. Indeed, it was reported that three Hermite functions enable the recovery of 98% of the QRS energy in control subjects. In our implementation, four Hermite functions were used in HCM because of the greater QRS heterogeneity found in HCM patients. They were defined as:
where n is the order of the Hermite function
and of the associated Hermite polynomial H, and a is the width parameter.
The QRS was therefore expressed as a linear combination of the first four Hermite bases and a reconstruction error:
where
is the reconstructed QRS signal, b n (t) is the Hermite function of order n, t is the time samples from T = 1 to 180 ms,
is the Hermite coefficients in the linear combination, and v(t) is the reconstruction error.
The width of the Hermite functions, allowing the consideration of a larger variability in QRS duration, was computed for each subject by minimizing the fitting error, which is defined as the root mean square of the difference between the reconstructed and original QRS.
From this Hermite transform characterization, five biomarkers, now referred to as morphologic QRS biomarkers , were computed in each lead for each subject:
The four coefficients of the Hermite basis required to reconstruct the QRS, providing a compact representation of the morphology of the QRS.
The fitting error, defined as the root mean square of the difference between the reconstructed QRS and the original signal, providing a measure of the difficulty of reconstructing the QRS from four Hermite basis.
The width parameter of the Hermite basis was not included as a feature because it did not show any significant difference between subjects (14.9 ± 1.2 for controls, 15.1 ± 1.6 for HCM; P = .53).
Similarly, all ST-T biomarkers were calculated per lead from the average ST-T waveform obtained after preprocessing the ECG signal. Six standard ST-T biomarkers were defined as follows:
T wave amplitude was defined as the absolute value of the difference between the maximum and minimum of the T wave values.
ST segment elevation was measured at the J point (defined as the junction between the end of the QRS complex and the beginning of the ST segment) plus 80 ms (because the heart rate was <120 beats/min).
The QTc interval was defined as the duration between the beginning of the QRS and the end of the T wave, corrected with Bazett’s formula (the most clinically used correction) in each lead.
The JTc interval was defined as the duration between the J point and the end of the T wave and was corrected with Bazett’s formula in each lead.
The T peak to T end interval was defined as the duration between the peak of the T wave and the end of the T wave in each lead.
T wave inversion was defined as a negative inflexion of at least 0.1 mV in at least two contiguous leads in V 3 to V 6 .
For the computation of these biomarkers, ECG waveform onsets and offsets (such as QRS beginning and end and T wave beginning and end) were obtained from the delineation algorithm.
In addition, the ST-T segment was characterized using a set of mathematical functions known as the Karhunen-Loève transform (KLT). This orthogonal linear transform is well established in reconstructing the ST-T segment. It provides a meaningful representation of the shape of the ST-T waves by maximizing the energy of the ST-T population and concentrating the signal information in a minimum number of parameters. , At the difference of the Hermite transform, the KLT is signal dependent. Indeed, it must be derived from the statistics of the signal (in this case, ST-T segments). A training data set is therefore required to compute the KLT bases. The KLT bases are then computed as the orthogonal eigenvectors of the covariance matrix of the training data set. In this work, we used a set of bases already computed in a previous study over a large independent data set of 200,000 preprocessed ST-T waveforms. Ninety percent of the signal energy can be reconstructed using four KLT coefficients, motivating the use of four KLT coefficients in this work for the reconstruction of the ST-T waveforms.
Five KLT-based ST-T biomarkers were therefore computed:
The four coefficients of the KLT basis required to reconstruct the ST-T
The fitting error, defined as the root mean square of the difference between the reconstructed and the original ST-T, to provide a measure of the difficulty of reconstructing the ST-T from only four KLT basis functions
Dimensionality reduction and blinded unsupervised clustering were performed to investigate patient subgroups in the HCM population. Each patient was represented using a vector of QRS biomarkers (and in a later stage, with additional ST-T biomarkers). Seven significant features were selected, using the unsupervised multicluster feature selection algorithm (MCFS) to discriminate the data set. To ensure proper comparison, Hermite coefficients were normalized using QRS amplitude for each patient. MCFS aims at preserving the multicluster structure of the data and relies on spectral analysis techniques combined to optimization-solving methods such as L1-regularized least square. The selected features were then reduced to two dimensions using Laplacian eigenmaps dimensionality reduction. This data-driven dimensionality reduction technique aims at extracting the low-dimensionality structure of the data from the high-dimension data set, hypothesizing that the data lie in a low dimension manifold. It preserves the data’s local geometrical properties by building an adjacency matrix, representing the neighboring connections between the data points d 1 …d k in our case, which are the morphologic QRS biomarkers for the k = 86 patients. This preservation of the locality structure makes the method resistant to outliers and noise. Each data point is then connected to the others based on their proximity (after the heat kernel), creating a graph W such as:
with N i and N j as the n-nearest neighbors (n ∈ N) of d i and d j, and t ∈ R as the parameter of the heat kernel.
The Laplacian matrix is defined as:L = D – WwithD ii =
The aim is to construct a set of points y 1 … y k , living in the low-dimensional manifold (in our case, two dimensions [2D], because we are looking to reduce the data set to 2D for visualization purposes) that can represent d 1 … d k . This means minimizing the objective function
so that points in the low-dimension space are close if close in the initial space. The embedding map is therefore computed by calculating the eigenvectors of the eigenvalue problem:
The embedding on the low m - dimensional space then obtained is
A density-based clustering algorithm, DBSCAN, was applied on this low-dimensional representation of the data set to investigate the existence of distinct subgroups. This algorithm identified clusters by maximizing the density in each of the clusters. The minimum number of individuals in a cluster was set to [m/25] = 3, with m = 86 HCM patients, as recommended. The distance between points in the clusters was evaluated using the Euclidean distance.
In the tables presented in this chapter, data are expressed as the mean with or without standard deviation or median and range. Data were tested for normality using the Kolmogorov-Smirnov test. Normally distributed data were compared using t -tests or analysis of variance. Nonnormally distributed data were compared using the Mann-Whitney U test or Kruskal-Wallis test. Categorical data were compared with chi-square or Fisher’s exact tests. Statistical significance was assumed when P was less than .05 (after Bonferroni adjustment for multiple comparisons, where appropriate).
All CMR imaging was performed at 3 Tesla (TIM Trio, Siemens). Cine imaging was acquired using standard methods. LV volumes, function, mass, and maximum segmental wall thickness at end diastole were analyzed using cmr42 (Circle Cardiovascular Imaging).
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here