Clinical Enzymology - Clinical Tree

Key Points

Enzymes are protein catalysts utilized by essentially all mammalian cells in specific biochemical reactions in different organs of the body, which may also be physically located in different organelles and structures within a cell.
Enzymes lower the activation energies of the chemical reactions that they catalyze so as to cause greatly enhanced rates of reaction. They do not become modified in these reactions and do not affect the equilibrium between reactants and products in the reaction.
Most enzymes have a practical or trivial name as well as a name based on standardized nomenclature of the International Union of Biochemistry; the latter is based on the type of reaction catalyzed by the enzyme.
Along with certain narrow ranges of pH, temperature, and protein and salt concentrations, most enzymes require additional organic molecules and/or inorganic ions for optimal enzyme function.
An understanding of enzyme kinetics allows for laboratory measurement of serum and other body fluid enzyme levels, as well as determination of possible enzyme inhibition.
Transition state theory of enzyme action has resulted in major breakthroughs in drug design.
Damaged or dying cells within organs can release enzymes into the circulation. These plasma enzyme levels can be used clinically to develop a differential diagnosis of a patient with respect to specific organ disease and dysfunction.
In addition, many enzymes have isozymes (i.e., polypeptide chains that differ in sequence but have similar enzymatic activity). Some enzymes are composed of two or more different polypeptide chains, such as the M and B chains of creatine phosphokinase, giving rise to isozymes that differ in chain composition (e.g., the MM, MB, and BB forms of creatine phosphokinase). In a number of diseases, specific isozymes become elevated in serum, facilitating diagnosis.

General Properties of Enzymes

All enzymes are proteins and function as catalysts. This means that they accelerate the rates of chemical reactions in the body but do not become chemically altered themselves in these reactions. Virtually every reaction that occurs in the body, both intracellularly and extracellularly, is catalyzed by an enzyme. The molecule for which a particular enzyme catalyzes a reaction is called the substrate . As explained later, enzymes interact very specifically with their substrates and, with the possible exceptions of closely related molecules, do not interact with any molecules other than their substrates. The concentrations and/or activities of different enzymes in blood give vital information about the functioning of specific tissues. Furthermore, many enzymes exist predominantly in specific tissues and not in other tissues. Thus, certain enzymes can serve as biomarkers for diseases in specific tissues. Therefore, a vital focus of the medical laboratory is determination of the concentrations and/or activities of specific enzymes in blood and other body fluids. The fact that an enzyme interacts selectively with only specific substrates facilitates determination of enzyme concentrations. The concentration of an enzyme can be determined simply by adding a specific substrate to serum or other body fluid and observing the rate at which the substrate disappears or the product of the reaction forms. This chapter is concerned with the principles of how enzyme concentrations are determined.

Catalysis

A catalyst accelerates the rate of a chemical reaction. The acceleration may occur in solution, and the process is called homogeneous catalysis . Catalysis on an insoluble surface is termed heterogeneous catalysis . Biological catalysts are called enzymes and for the most part are proteins that exhibit homogeneous catalysis. However, some enzymes are embedded in membrane structures and should be considered insoluble, heterogeneous catalysts.

Enzyme Specificity

Enzyme specificity defines the capacity of protein catalysts to recognize and bind only one or a few molecules, the substrate(s), excluding all others, a process referred to as binding specificity . An enzyme catalyzes a unique chemical process (i.e., a solitary type of covalent bond is broken or formed). This is called reaction specificity . Most enzymes exhibit absolute reaction specificity, that is, no minor by-products are formed. Binding specificity permits many biochemical reactions to occur simultaneously within the same biological space. Absolute reaction specificity saves energy because it reduces the pool of unwanted metabolites.

Enzymes are stereoselective because of the asymmetry of their active sites. They recognize only one enantiomeric form (i.e., one of a pair of compounds having a mirror image relationship) of a chiral substrate. Hence, proteases exclusively bind polypeptides made up of l -amino acids (and not d -amino acids) and catalyze their hydrolysis. Enzymes exhibit geometric specificity exemplified by the fumarase reaction, in which the Krebs cycle intermediate, fumarate (the trans isomer), but not maleate (the cis isomer), undergoes hydration.

Enzyme Concentration And Activity

The concentration of enzyme molecules within a given intracellular or extracellular space depends on their rate of synthesis and degradation. Control of enzyme synthesis occurs at both transcriptional and translational levels. In eukaryotes, cells of different organs express different isoforms, called isozymes (discussed later), of the same enzyme, which alters rates and specificity suitable for selective cellular homeostasis. The presence of substrate, or other inducing molecules, can cause a sudden increase in enzyme levels.

Enzymatic activity is also subject to control through the binding of small molecules that produce conformational changes in the structure of the enzyme. This binding can alter substrate affinity for the enzyme or change the enzyme’s catalytic activity, or both. Generally, enzymes that catalyze rate-determining steps in metabolic pathways are subject to this type of regulation.

Enzymes do not affect the value of the equilibrium constant between reactants and products. In a reversible reaction, they accelerate forward and reverse reactions by the same relative amount. The equilibrium distribution of reactants and products is unchanged whether the equilibrium state has been achieved in the presence or absence of an enzyme.

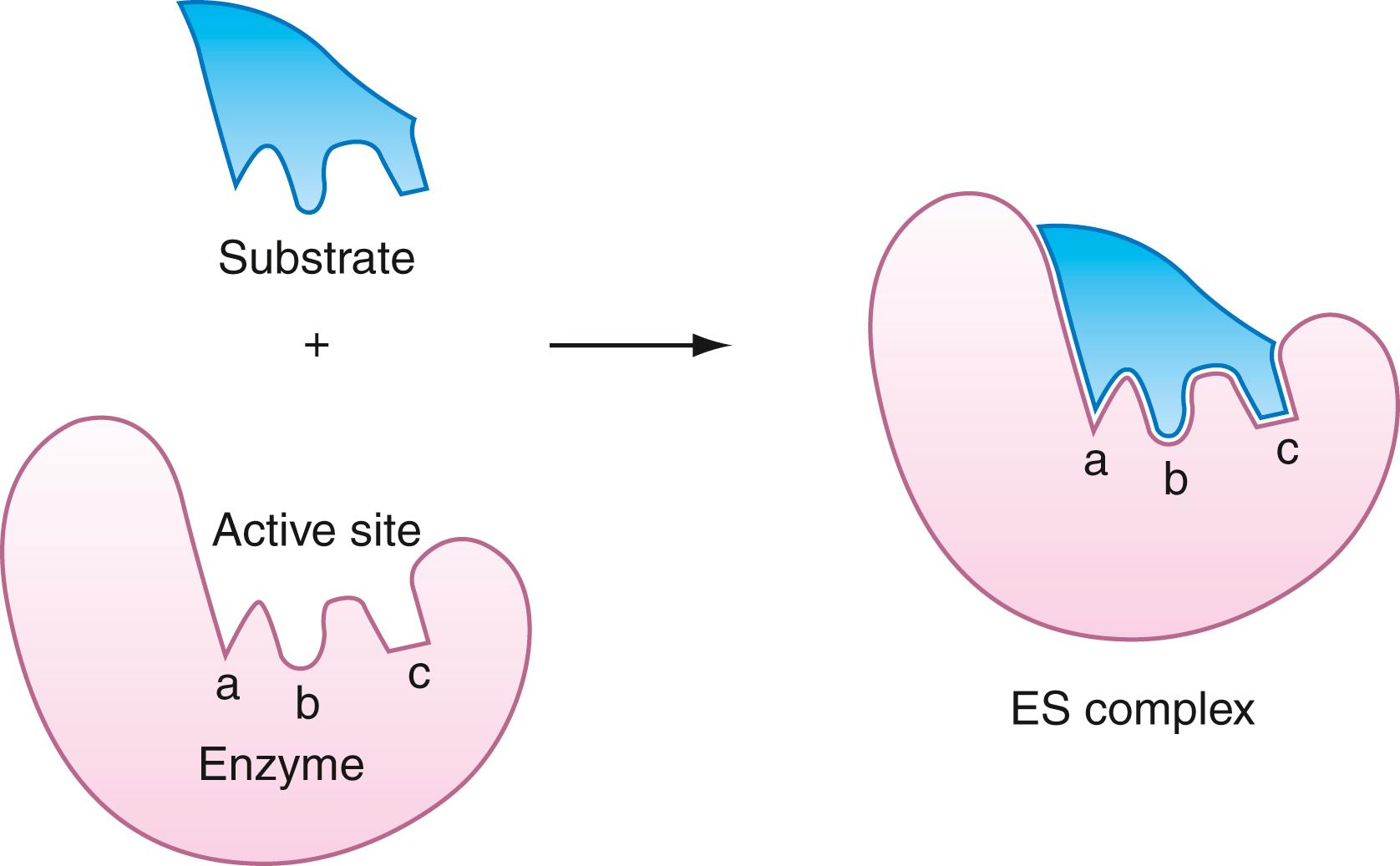
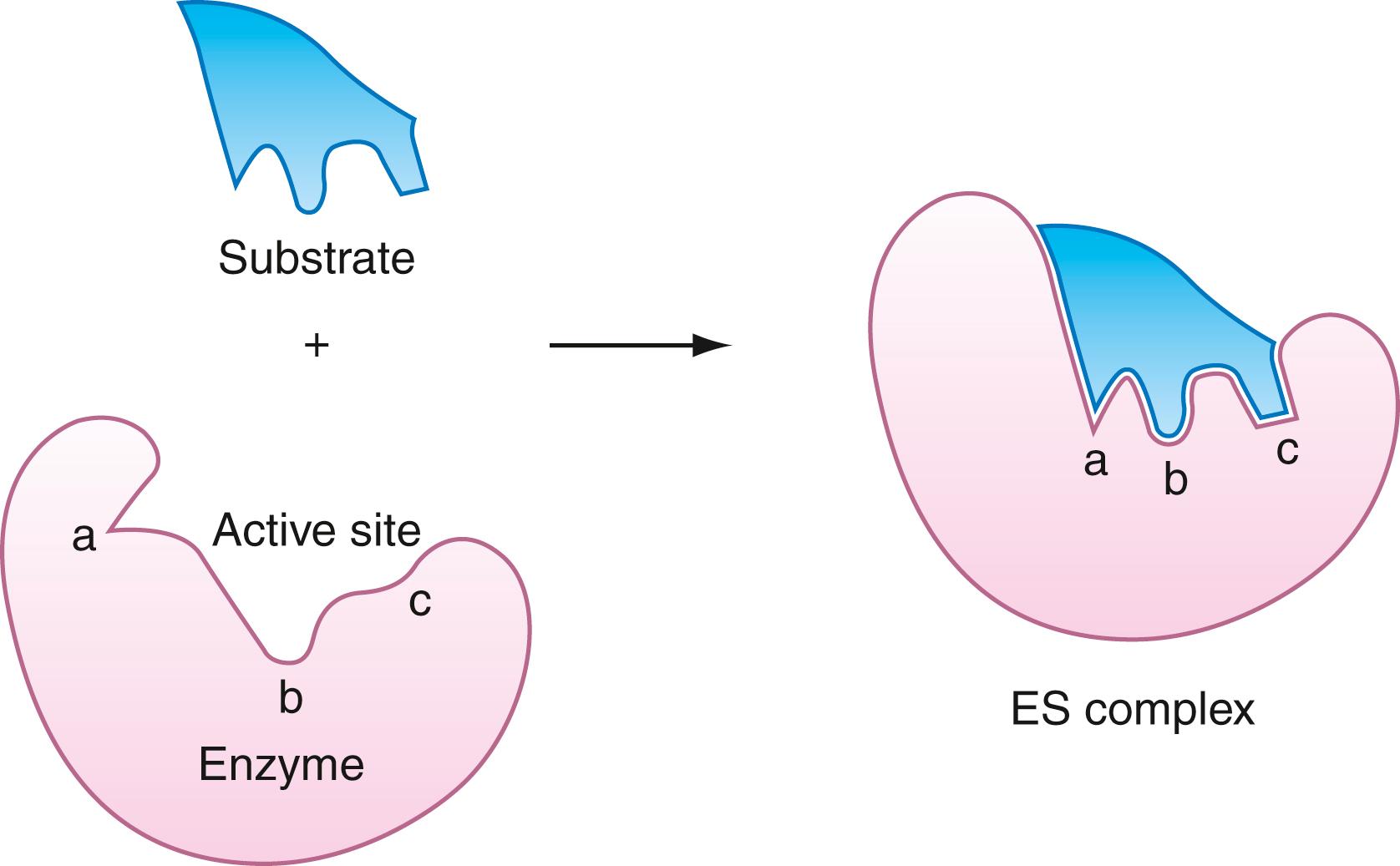
As noted previously, almost all known enzymes are proteins or conjugated proteins. A few enzymes are nucleoproteins, which are ribonucleic acid (RNA) molecules complexed to proteins. Enzymes contain a surface region referred to as the active site , where binding and catalysis occur. It is a cleft or crevice in which are embedded specific groups, suitably oriented, which carry out the roles of binding and bond-making, or bond cleavage. The three-dimensional shape of the active site is a vital determinant in the recognition and specificity process. The enzyme-substrate complex is the adduct formed by the physical adsorption of the substrate to the active site. Enzyme-substrate complex formation requires specific alignment of atoms in the active site with atoms in the substrate molecule. This complementary arrangement is referred to as the lock-and-key fit of the substrate in the active site and is illustrated in Figure 21.1 . Sometimes, the shape of the substrate molecule does not exactly match the contour of the active site. Yet, the substrate binds tightly because of its capacity to reshape the active site to a conformation that binds the substrate with high affinity. This type of substrate adsorption is described as induced fit . It is illustrated in Figure 21.2 . Active sites of induced-fit enzymes become complementary only after the substrate is bound. Some of the favorable binding energy is used in reorganizing the shape of the active site.

Figure 21.1, The lock-and-key model of substrate binding to the enzyme active site. The enzyme exhibits preformed steric and electronic complementarity to the shape and charge distribution of the substrate. No shape changes or electronic redistributions in the enzyme or the substrate are necessary for optimal binding.

Figure 21.2, The induced-fit model of substrate binding to the enzyme active site. The induced-fit model postulates an initial weak, flexible interaction of the substrate with groups in the enzyme’s substrate (ES) binding site. This is sufficient to trigger a conformational rearrangement of the enzyme’s surface that exposes additional ligand binding groups that enhance the binding affinity of the substrate for the enzyme.

Molecular Basis For Enzyme Catalysis

The free energy of activation is the energy absorbed by reactant molecules before they have a chance to convert to products. The free energy of activation is a barrier to chemical reactivity. When this barrier is large, the rate of a chemical reaction is very slow. The lower the barrier, the faster is the reaction rate. The barrier exists for almost all chemical reactions because, for bonds to be broken, they must be stretched and sometimes bent away from their equilibrium positions. These deformations require energy. Enzymes lower the free energy of activation. Most metabolic reactions have very high activation barriers and, in the absence of enzymes, reaction rates are imperceptibly slow. Cells can selectively reduce metabolic reaction rates to near zero by abolishing enzyme activity. This feature of metabolism allows cells to “turn on” and “turn off” metabolic pathways during different stages of the cell cycle. Enzymes lower the free energy of activation in various ways. Binding and appropriate orientation of the substrate in the active site increase its proximity to the catalytic groups. Various types of catalysis are used by enzymes. The major types of catalysis are acid-base, electrophilic, nucleophilic, elimination reactions, decarboxylation reactions, and metal ion and electrostatic catalysis. Reductions in the free energy of activation occur through preferential binding of the transition state (or intermediate enzyme-substrate complex) to active site groups. The side chains of different amino acids participate in catalysis. The side chain of histidine is an effective acid-base catalyst, and the side chains of serine, cysteine, lysine, histidine, and aspartic acid participate in covalent catalysis. The side chains of lysine and arginine, as well as metal ions, can act as electrostatic catalysts by stabilizing negative charges that develop during catalysis. Conversely, the side chains of aspartate and glutamate residues can stabilize the positive charges that develop during catalysis.

The rate of the reaction is proportional to the concentration of molecules that have attained energy equal to the free energy of activation, ΔG‡. This energy is higher for the uncatalyzed reaction. The idea that enzymes accelerate chemical reactions by lowering ΔG‡ is illustrated in Figure 21.3 , where the free energy needed for a productive reaction is compared for an uncatalyzed and an enzyme-catalyzed reaction. As shown in this figure, enzymes lower the activation energy. As explained later, an enzyme binds to its substrate to form an enzyme-substrate complex in an initial recognition step. In the subsequent step, the substrate is converted to product. The enzyme-substrate complex is more stable than the two separated species (i.e., has a lower free energy). However, this energy cannot be too low, as in the case of the dotted lines in Figure 21.3 , because, in this case, the activation energy would be raised and the reaction rate would be slower. As explained later, an enzyme binds to what is called the transition state on the reaction pathway. This is the reactive form of the substrate that is of relatively high free energy compared with the free energy of the ground state of the substrate. Thus, although the energy of the substrate is raised in the transition state complex, the enzyme provides stabilizing interactions with the transition state that result in overall stabilization of the complex and in an enhanced rate of reaction.

Figure 21.3, The free energy path of a reactant molecule through its transition state on its way to becoming a product molecule. The energy trajectory followed by a molecule undergoing a chemical reaction is the minimum free energy pathway known as the reaction coordinate . The transition state, the state of highest free energy, is the point where there is an equal probability that a reaction will take place, or that the activated complex will decompose back to the reactant. The free energy change, ΔG‡, is the energy that the substrate molecule must acquire to reach the activated complex, also called the activation energy barrier. A, The uncatalyzed reaction. The reactant, called S , must acquire the necessary energy, ΔG‡, to become converted into the product, P. This energy is the difference between the energy of the transition state and the ground-state energy of S. B, The enzyme-catalyzed reaction. In this case, the enzyme binds noncovalently to the substrate, resulting in a stable enzyme–substrate (ES) complex. In most textbooks, the ES complex is shown as having slightly higher energy than that for free E and S. This is because the energy of the substrate increases when it binds to the enzyme because the enzyme recognizes the transition state of the substrate (discussed later), which is a higher energy form for the substrate. However, overall, the energy of the ES complex is lower than that for the free enzyme and free substrate, as reflected in the favorable affinity constant (usually measured as 1/K M , explained later) for the binding of S to E. This is why the energy of ES is shown as lower than for the two isolated species. However, although this complex has a lower free energy than that for the two separated species (S and E), it should not be too much lower, as discussed later. The energy of activation, ΔG‡, now becomes the difference in energy between that of the transition state in the ES complex, and not for S alone, and that of the ground-state ES complex. This energy is less than that for the uncatalyzed reaction. A major reason why ΔG‡ for the enzyme-catalyzed reaction is less than for the uncatalyzed reaction in A is that the enzyme has a high affinity for the transition state, lowering its energy relative to that for the ground-state ES complex. Note in B what would happen if the enzyme had a very high affinity for ground-state ES (broken line). If the same transition state is assumed, the energy barrier to reach this transition state, instead of just being ΔG‡, will now be ΔG‡ + ΔG‡′, resulting in a slower rate of reaction.

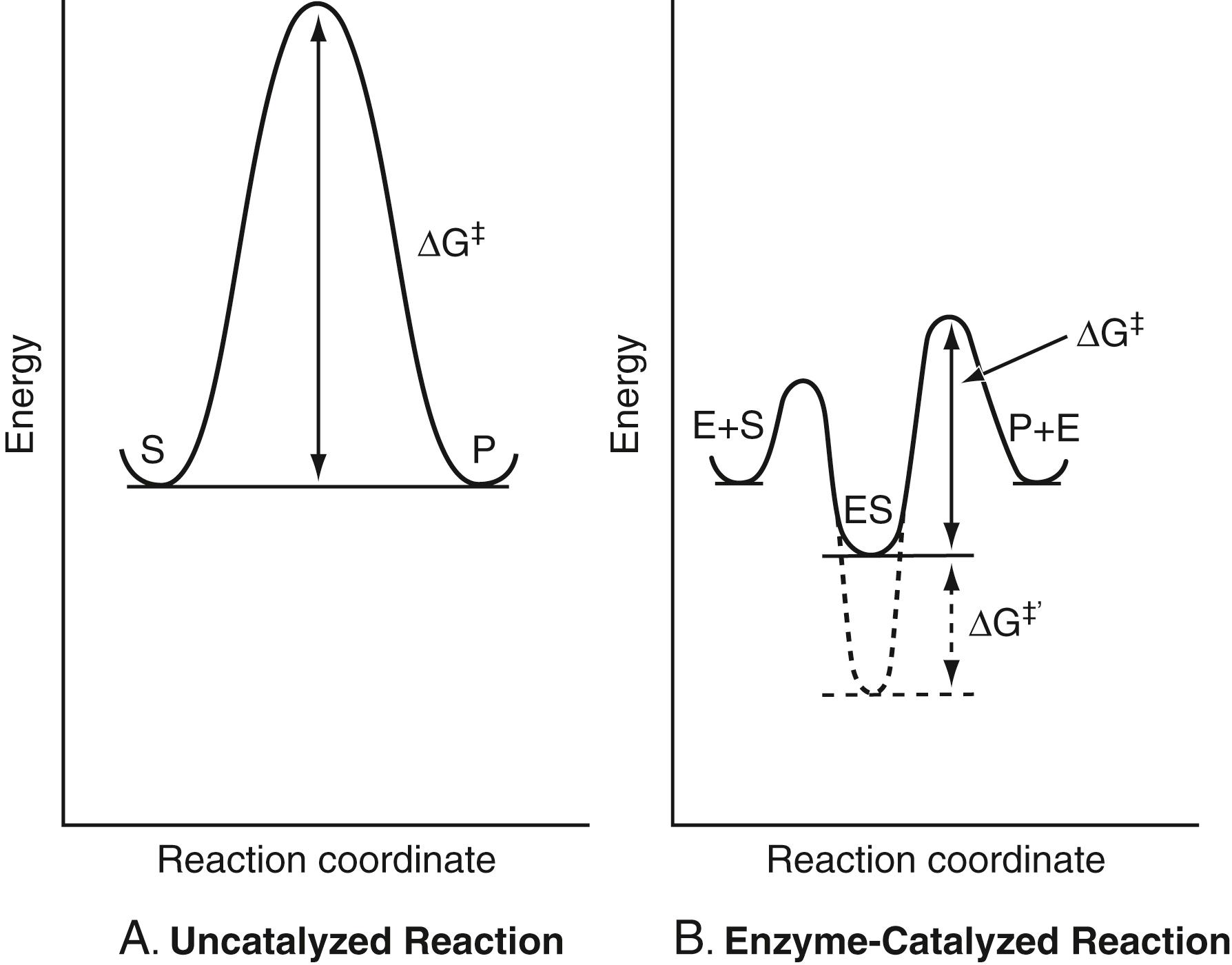
Enzymes have developed as extremely efficient catalysts because their active sites have evolved to bind transition states very tightly. It is this tight binding that stabilizes the transition state and lowers the free energy of activation. Enzymes do not alter the ground state energies of reactants and products of a chemical reaction. The equilibrium state is characterized as a state of lowest energy; the composition of the reactant and product mixture at equilibrium is a reflection of these ground state energies. Enzymes emerge from the catalytic process unaltered, although some undergo transient chemical modification during the reaction.

Nomenclature of Enzymes

The nomenclature of commonly measured enzymes was standardized by the Enzyme Commission (EC) of the . Each enzyme has two names: a practical or trivial name and a systematic name. The latter consists of a unique numeric code designation and the nature of the catalytic reaction, as follows: Enzymes are named by citing the name of the substrate molecule and by following that with the suffix, -ase; sometimes the name also includes a designation of the type of reaction catalyzed. Examples are as follows.

1.
RNA is hydrolyzed by an enzyme called ribonuclease.
2.
Lactic acid is oxidized to pyruvic acid by an enzyme called lactic acid dehydrogenase.

Older trivial names persist in the literature. Examples are trypsin, a protein-hydrolyzing enzyme secreted into the gut, and papain, a plant enzyme that also hydrolyzes proteins. A more systematic classification of enzymes has been implemented in the biochemical literature ( ). Enzymes have been organized by reaction type into six major classes, as shown in Table 21.1 .

TABLE 21.1

Enzyme Classification

Class	Type of Reaction Catalyzed
1. Oxidoreductases	Oxidation-reduction reactions
2. Transferases	Transfer of functional groups
3. Hydrolases	Hydrolysis reactions
4. Lyases	Group elimination to form double bonds
5. Isomerases	Isomerizations
6. Ligases	Bond formation coupled with ATP hydrolysis

ATP, Adenosine triphosphate.

Isozymes

Many enzymes have isoenzymes, called isozymes, of different forms that catalyze the same reaction. These different forms occur because of differences in the amino acid sequences of enzymes. Despite these differences in sequence, the enzymes fold to the same three-dimensional structures and frequently exhibit similar affinities for and catalytic rates with substrates. Often, isozymes occur as the result of differences in the chain composition of enzymes, as discussed later. Most commonly, different isoenzymes are found in specific organs or tissues; determination of the type of isoenzyme present can then be of use in identifying the damaged tissue and releasing the enzyme. The standard nomenclature of isoenzymes is based on their electrophoretic migration, with the isoenzyme migrating farthest toward the anode designated isoenzyme 1 . The most widely recognized isoenzymes are those that are composed of varying combinations of subunits; common examples are creatine kinase (CK), a dimer of muscle (M) and brain (B) subunits, and lactate dehydrogenase (LD), a tetramer of heart (H) and M subunits. In other cases, isoenzymes may have the same protein component but may differ based on modifications made by the cell of origin. For example, the bone, renal, and liver isoenzymes of alkaline phosphatase (ALP) have identical amino acid sequences but differ in carbohydrate composition.

In some cases, isoenzymes may have completely different protein structures. Distinct cytoplasmic and mitochondrial isoenzymes of both CK and aspartate aminotransferase (AST) have markedly differing structures. Placental and intestinal ALP isoenzymes have a different protein structure compared with that of the tissue-nonspecific forms found in liver, bone, and other organs.

Finally, enzymes can be modified by proteases present in serum to produce forms that differ slightly from each other; these are termed isoforms . As an example, CK-M subunits are partially metabolized by carboxypeptidase N, removing a lysine residue from the carboxy-terminal end of the molecule and converting the tissue isoform to a differently charged plasma isoform. The relative amounts of the tissue and plasma isoforms can be used as a marker of duration of injury to CK-containing cells. The official names and EC numbers of the commonly measured, clinically useful enzymes are given in Table 21.2 ( ).

TABLE 21.2

Names, Enzyme Numbers, Substrates for Enzymes

Enzyme (IUB Group, EC Number)	Substrate	Comments
AChE (hydrolase, EC 3.1.1.7)	Acetylcholine, acetyl thiocholine; hydrolyzes acetyl-β-methylcholine	Choline is HO-CH ₂ -CH ₂ -N ⁺ -(CH ₃ ) ₃ , a quaternary amine; many esters with the OH group are substrates. Critical in regulating acetylcholine neurotransmission.
PChE (hydrolase, EC 3.1.1.8)	Many aliphatic esters of choline; unlike AChE, does not hydrolyze acetyl-β-methylcholine but, also unlike AChE, does hydrolyze butyryl- and benzoylcholine.	Largely unknown function; it is critical in hydrolyzing the muscle relaxant succinylcholine.
ACP (hydrolase, EC 3.1.3.2)	G6P, phenyl-P, 3-glycerophosphate, phenolphthalein-P, thymolphthalein-P, naphthol-P	Cleaves phosphate esters like ALP (see next entry) but at pH values around 5.0.
ALP (hydrolase, EC 3.1.3.1)	See ACP	ALP has unusual pH optimum of about 9. Optimum pH varies with substrate and buffer.
ACE (bradykinin, hydrolase, EC 3.4.15.1)	Splits C-terminal His-Leu dipeptide of angiotensin 1 to yield angiotensin 2; also splits hippuryl-His-Leu to hippurate + His-Leu.	Considered a nonspecific hydrolase; acts on Met- and Leu-enkephalin.
LD (oxido reductase, 1.1.1.27)	Pyruvate and other keto acids + NADH Also lactate and other 2-hydroxy acids + NAD ⁺	Moderately specific
5′-Nucleotidase (hydrolase, EC 3.1.3.5)	5′-Monoribonucleotides	Wide specificity for 5′-monoribonucleotides

ACE, Angiotensin-converting enzyme; AChE, acetylcholinesterase; ACP, acid phosphatase; ADP, adenosine diphosphate; ALP, alkaline phosphatase; ATP, adenosine triphosphate; EC, Enzyme Commission; G6P, glucose-6-phosphate; IUB, International Union of Biochemistry; LD, lactate dehydrogenase; NAD ⁺ , nicotinamide-adenine dinucleotide; NADH, the reduced form of NAD ⁺ ; P, phosphate; PChE, pseudocholinesterase; pNPP, p -nitrophenylphosphate.

Enzyme Cofactors

Two-thirds of all enzymes contain cofactors that are a group of heat-stable substances required for catalysis. They are low-molecular-weight organic molecules and inorganic ions. The combination of cofactor plus the protein portion, the apoenzyme, forms the complete catalytic entity and is known as the holoenzyme . Organic cofactors are bound covalently or noncovalently to the apoenzyme. Covalently bound cofactors are sometimes referred to as prosthetic groups . Cofactors are observed in oxidation-reduction, group transfer, and isomerization reactions, and in reactions that form covalent bonds. Hydrolytic reactions generally do not require cofactors. Organic cofactors are listed in Table 21.3 . Inorganic cofactors that include mainly metal ions are listed in Box 20.1 . A cosubstrate is an organic cofactor that behaves as a second substrate in an enzyme-catalyzed reaction. Cofactors such as nicotinamide adenine dinucleotide (NAD ⁺ ) can serve as cosubstrates for many oxidoreductases. A single molecule of NAD ⁺ may act as a cosubstrate many thousands of times. The product, NADH (reducing agent derived from NAD ⁺ ), must first be oxidized back to NAD ⁺ before it can participate again as an electron and H atom acceptor. The recycling of the NAD-NADH oxidation-reduction couple depends on the ready availability of a chemical system capable of regenerating NAD ⁺ from NADH. A substrate molecule is usually irreversibly changed in a reaction. In contrast, cosubstrate molecules are recycled.

TABLE 21.3

Enzyme Cofactors

Coenzyme(s)	Reaction Type	Deficiency
Coenzyme A	Acyl transfer
Thiamine pyrophosphate	Aldehyde transfer	Beriberi
Folic acid coenzymes	One-carbon transfer	Megaloblastic anemia
Cobamide (B ₁₂ ) coenzymes	Alkylation	Pernicious anemia
Nicotinamide coenzymes	Oxidation-reduction	Pellagra
Flavin coenzymes	Oxidation-reduction
Biotin	Carboxylation
Lipoic acid	Acyl transfer
Pyridoxal phosphate	Amino group transfer
Coenzyme Q	Electron transfer

Box 21.1

Inorganic Cofactors for Enzymes

Mg ⁺⁺
Fe ⁺⁺ /Fe ⁺⁺⁺
Zn ⁺⁺
Cu ⁺ /Cu ⁺⁺
Ca ⁺⁺
Mn ⁺⁺
Co ⁺⁺

Factors Affecting Plasma Enzyme Activities

Plasma levels of enzymes may be increased by several mechanisms. Because enzymes are high-molecular-weight compounds, the most common cause for increased plasma enzymes is death of enzyme-containing cells. As cells die, activation of phospholipases leads to development of holes in the plasma membrane, allowing leakage of cytoplasmic macromolecules, such as proteins. Enzymes are also released in the process of normal cell turnover; this is thought to be the source of normal plasma levels of various enzymes. Increased synthesis of enzymes by cells also leads to increased plasma enzyme levels. With increased activity of osteoblasts, plasma levels of the bone isoenzyme of ALP increase. This may be responsible for the increase in muscle-related enzymes seen with increased exercise ( ). Many drugs that stimulate microsomal enzymes, including ethanol and antiepileptic agents, lead to increased plasma γ-glutamyl transferase (GGT). In some cases, release of enzyme from cells occurs without cell death or increased synthesis.

As discussed in Chapter 22 on liver function, acute liver injury from trauma, hepatitis, or toxic compounds such as ethanol causes release into blood of the aminotransferases, AST and ALT, and LD from damaged and necrotic hepatocytes. For ethanol, which also induces not only cellular damage but also mitochondrial damage to hepatocytes, there is likewise consequent release of the mitochondrial isoenzyme of AST, MT-AST, into blood. Where there is a blockade of bile flow, as occurs from stones in the common bile duct, retrograde buildup of bile salts induces membrane damage to hepatocytes and bile ductule epithelial cells at the cell-cell junction. This results in the release into blood of a number of liver enzymes, such as ALP, leucine aminopeptidase (LAP), and 5′-nucleotidase (5′-NT), which are bound to the canalicular membrane, and GGT, which is bound to the hepatocyte membrane at this junction.

Ischemia of myocardial cells leads to loss of troponin, CK, including the MB isozyme of CK, and glycogen phosphorylase into plasma. Ingestion of food leads to release of intestinal ALP into lymphatic fluid and may transiently increase plasma levels of ALP. Increased concentrations of bile salts with canalicular obstruction may release fragments of membrane with enzyme attached into the circulation or may solubilize the membrane-binding domain ( ). Finally, increased plasma enzyme levels may be due to decreased clearance of enzymes from the circulation. Some smaller enzymes, such as amylase and lipase, are partially cleared by glomerular filtration; renal failure increases their plasma levels. For many enzymes, autoantibodies against one or more isoenzymes may cause the development of enzyme–antibody complexes (often termed macroenzymes ), which result in enzyme half-lives similar to the 3-week half-life of immunoglobulin G ( ). Most commonly, no specific clinical feature is associated with such macroenzymes. However, it is common to see antibodies against the intestinal isoenzyme of ALP in persons with bacterial infection ( ). A similar phenomenon can occur when enzymes are bound to antibodies directed against other antigens, such as LD complexes with antibodies to streptokinase ( ).

Factors Affecting the Lifetime Of Enzymes In Blood

The time course of appearance and disappearance of enzymes with cell injury is dependent on a number of factors. With cell death, defects in cellular membranes enlarge gradually over time; thus, smaller cytoplasmic enzymes will leak from damaged cells sooner than larger ones. For example, with myocardial injury, CK and AST are smaller than LD and appear in plasma sooner. Some enzymes are not cytoplasmic but may be within mitochondria (isoenzymes of CK and AST) or bound to plasma membranes (such as ALP and GGT); cell death typically does not lead to release of such enzymes. If cell death is due to infarction caused by interruption of blood flow to a portion of an organ, enzymes released from damaged cells must diffuse away from the nonperfused region before appearing in the circulation. For example, in myocardial infarction, CK peaks later in persons whose coronary arteries are not successfully reperfused by the use of thrombolytic agents. The degree of elevation of an enzyme is related to the number of cells injured, the gradient in concentration between cell and plasma, and the rates of enzyme entry into and clearance from plasma. In myocardial infarction, the amount of CK released is strongly correlated to size of infarction; thus, enzyme levels with one-time injury are related to the amount of cell injury occurring. If injury is ongoing, plasma enzyme levels will continue to be elevated for a longer time period. For example, in acute hepatic injury, the time course of enzyme changes can be used to differentiate viral hepatitis, in which immunologic damage causes ongoing cell death and prolonged enzyme elevation, from ischemic and toxic injury, in which damage is immediate but short-lived and enzyme elevations rapidly return to normal.

Other important determinants of the time course of enzyme changes include the relative gradient in enzyme levels between cells and serum and the rate of clearance of enzyme from plasma. For any given amount of cell damage, the enzyme with the higher gradient between cells and serum will show greater elevation of plasma levels. For example, with hepatocyte injury, AST levels in hepatocytes are higher than those of alanine aminotransferase (ALT), and both are many times higher than levels of LD. Immediately after injury, therefore, AST will show a greater degree of elevation than will ALT, and LD will show the least degree of increase. In cardiac tissue, the gradient of CK between myocardial cells and plasma is several times higher than that for LD, leading to higher peak CK than LD levels. Once an enzyme reaches plasma, the rate of clearance also becomes important. For example, the half-life of AST is much shorter than that of ALT, and the half-life of CK is shorter than that of the cardiac isoenzymes of LD. With hepatic injury, therefore, plasma ALT often becomes higher than AST within a short time after injury. Following myocardial infarction, CK returns to normal several days earlier than does LD.

Enzyme Kinetics: Determination Of Total Enzyme Concentrations In Serum And Other Body Fluids

The basic objective of clinical enzymology is the determination of the total concentrations of specific enzymes in serum and other body fluids. Qualitatively, detecting the presence of enzymes in body fluids is fortunately quite simple because each enzyme has almost total specificity for one or at most a few substrate(s). By adding the substrate, say, to serum, and observing either its disappearance or the appearance of the product, the presence of the enzyme can be ascertained. As is now explained, the rate at which substrate disappears or product appears can be directly used to determine the concentration of enzyme present ( , ; ; ; ; ).

Determination Of Total Enzyme Concentration In Serum And Other Body Fluids By Michaelis-Menten Equation

Enzymes exhibit saturation, which occurs when the rate becomes unresponsive to further increases in substrate concentration. Ordinary chemical reactions occur with rates proportional to the entire range of reactant concentrations. In an enzyme-catalyzed reaction, at low substrate concentrations, rates are proportional to substrate concentration. At higher concentrations, the rate does not increase in direct proportion. At still higher substrate concentrations, the rate becomes constant and unresponsive to any further change in substrate concentration. This led to the proposal that enzyme catalysis is a two-step process that consists of an initial adsorption whereby the substrate combines with the enzyme to form a noncovalent enzyme–substrate (ES) complex, followed by a second step in which the ES complex decomposes into product (P) and free enzyme (E) as follows:

E+S ⇄_{k_{-1}}^{k_{1}} ES \overset{k_{2}}{\to} P+E

$E+S ⇄_{k_{-1}}^{k_{1}} ES \overset{k_{2}}{\to} P+E$

The formation of enzyme–substrate may be regarded as the step in which the enzyme recognizes the substrate. This process involves the formation of specific noncovalent interactions between enzyme and substrate. These interactions include ionic interactions, hydrophobic interactions, hydrogen bonding, and van der Waals interactions.

The physical explanation for saturation is that binding reduces the number of active sites available to form the enzyme-substrate complex. When all sites are filled, no further binding can occur until an active site discharges its contents. The step that determines the overall rate is the k ₂ step. Adding additional substrate molecules under saturating conditions does not change the rate because all unbound substrate molecules must wait until an active site becomes vacant. This kinetic model is now used to derive the Michaelis-Menten equation that enables direct determination of total enzyme concentration or activity.

Derivation of the Michaelis-Menten Equation

The velocity, v, the rate at which product forms, of an enzyme-catalyzed reaction is defined as:

v= v_{0} =d [p] /dt= k_{2} [ES]

$v= v_{0} =d [p] /dt= k_{2} [ES]$

where t is time. Note that v is the initial velocity of the reaction, referred to as v ₀ , where we know the concentration of the substrate. It is important to measure initial velocities to ensure the absence of product inhibition (when time [t] = 0, [P] = 0) and the loss of enzyme due to proteolysis, denaturation, or time-dependent adsorption onto glass or plastic surfaces.

The differential rate law, which gives the rate of change of [ES] with time, is the difference between the rate of the k ₁ step leading to formation of the complex and the rates of the steps leading to the disappearance of [ES] and k ₁ and k ₂ steps:

d [ES] /dt = K_{1} [E] [S] - K_{- 1} [ES] - K_{2} [ES]

$d [ES] /dt = K_{1} [E] [S] - K_{- 1} [ES] - K_{2} [ES]$

For a wide variety of enzyme-catalyzed reactions, it has been found that, over long periods of time, after an initial transient phase lasting a few milliseconds, the concentration of the ES complex remains constant (i.e., does not change in time), especially when S >> E. This is the steady-state assumption. Therefore,

d (ES) /dt=0= K_{1} [E] [S] - K_{- 1} [E] [S] - k_{2} [ES] = K_{1} [E] [S] - (K_{- 1} + K_{2}) [ES]

$d (ES) /dt=0= K_{1} [E] [S] - K_{- 1} [E] [S] - k_{2} [ES] = K_{1} [E] [S] - (K_{- 1} + K_{2}) [ES]$

and

[ES] = K_{1} [E] [S] / (K_{-1} + K_{2}) = [E] [S] / K_{M}

$[ES] = K_{1} [E] [S] / (K_{-1} + K_{2}) = [E] [S] / K_{M}$

where the ratio of the rate constants k ₁ /(k ₋₁ + k ₂ ) is defined as 1/K _M . K _M is termed the Michaelis constant , whose significance is discussed later.

If E _T is the total concentration of enzyme, it is equal to free enzyme plus enzyme bound to substrate, that is,

[E_{T}] = [E] + [ES]

$[E_{T}] = [E] + [ES]$

Then, using Equation 21.5 ,

[E_{T}] = [E] + [E] [S] / K_{M}

$[E_{T}] = [E] + [E] [S] / K_{M}$

and

[E] = [E_{T}] / (1+ [S] / K_{M})

$[E] = [E_{T}] / (1+ [S] / K_{M})$

and substituting for [E] in Equation 21.5 ,

\begin{matrix} [ES] = [E] [S] / K_{M} \\ = [ET] / (1+ [S] / K_{M}) \times [S] / K_{M} \\ = [ET] [S] / (K_{M} + [S]) \end{matrix}

$\begin{matrix} [ES] = [E] [S] / K_{M} \\ = [ET] / (1+ [S] / K_{M}) \times [S] / K_{M} \\ = [ET] [S] / (K_{M} + [S]) \end{matrix}$

\begin{matrix} [ES] = [E] [S] / K_{M} \\ = [ET] / [(1+ [S] / K_{M}) [S] / K_{M}] . \end{matrix}

$\begin{matrix} [ES] = [E] [S] / K_{M} \\ = [ET] / [(1+ [S] / K_{M}) [S] / K_{M}] . \end{matrix}$

Combining Equation 21.9 with Equation 21.2 , we have

\frac{d [P]}{dt} = V_{0} = K_{2} [ES] = \frac{K_{2} [E_{T}] [S]}{(K_{M} + S)} .

$\frac{d [P]}{dt} = V_{0} = K_{2} [ES] = \frac{K_{2} [E_{T}] [S]}{(K_{M} + S)} .$

Equation 21.10 , termed the Michaelis-Menten equation, accurately describes virtually all single-substrate enzyme-catalyzed reactions and many bisubstrate reactions in which the concentration of one substrate is constant throughout the course of the reaction.

Total Enzyme Concentration Can Be Determined from the Initial Rate at Saturation

A typical plot of v ₀ versus initial substrate concentration is shown in Figure 21.4 . The curve is a rectangular hyperbola, and the initial rate increases up to a particular substrate concentration beyond which the rate remains constant. This occurs on the curve where [S] > > K _M . This is referred to as saturation , in which all of the enzyme molecules are bound to the substrate, making it impossible to increase the rate any further by increasing [S]. Note that S is free S, unbound to the enzyme. The only manner in which S can be greater than K _M is if the total concentration of S is greater than the total enzyme concentration.

Figure 21.4, The effect of substrate concentration [S] on the velocity (V) of an enzyme-catalyzed reaction. The plot is for an enzyme that obeys Michaelis-Menten kinetics, where the maximal velocity is V max and [S] equals K M where (v) equals V max /2.

Note that, where saturation occurs, that is, where [S] > > K _M , Equation 21.10 reduces to

d [P] /dt= V_{0} = K_{2} [E_{T}]

$d [P] /dt= V_{0} = K_{2} [E_{T}]$

Because the rate is constant at saturation, the rate is zero order with respect to substrate; the rate does not depend on the concentration of reactants. There is a dependence on E _T , which, however, is not consumed in the reaction. At saturation, the initial velocity of the reaction is referred to as the maximal velocity , or V _max = k ₂ E _T . Under this saturating condition, the initial rate of the reaction is directly proportional to the total enzyme concentration. If k ₂ is known, then E _T can be directly computed as the observed initial rate divided by k ₂ . This equation solves the problem of determining the total enzyme concentration from measurements of the rate of the enzyme-catalyzed reaction where [S] > > K _M .

Knowledge of k ₂ and K _M Allows Determination of [S] Values That Will Saturate the Enzyme

To fulfill the conditions of Equation 21.11 , it is necessary to know both K _M and k ₂ . These can be estimated from plots similar to the one shown in Figure 21.4 . To generate these plots, the purified enzyme is dissolved in aqueous solution in a series of tubes at the same concentration. A different concentration of substrate is added to each of these tubes, and the initial rate of reaction for each tube is determined using a suitable (mostly spectrophotometric) technique. The value of v ₀ versus initial substrate concentration [S] can be plotted; the value of S at which the rate levels off (i.e., becomes constant) can be estimated from the plot.

The Lineweaver-Burk Plot Gives k ₂ and K _M

The problem with this approach is that, in the v ₀ versus [S] plot, the rate approaches V _max asymptotically. Therefore, V _max can only be estimated, often inaccurately, from such a plot. A more accurate method by which to accomplish this goal is to linearize the Michaelis-Menten equation ( Eq. 21.10 ) by taking the reciprocal of both sides of the equation and rearranging the terms, that is,

\frac{1}{V_{0}} = \frac{K_{M}}{V_{MAX}} . \frac{1}{[S]} + \frac{1}{V_{MAX}}

$\frac{1}{V_{0}} = \frac{K_{M}}{V_{MAX}} . \frac{1}{[S]} + \frac{1}{V_{MAX}}$

As can be seen from Equation 21.12 , a plot of 1/v ₀ versus 1/[S], called the double reciprocal plot , also called the Lineweaver-Burk plot , should be linear; the Y-intercept should be 1/V _max , and the slope should be K _M /V _max . Because 1/V _max is the Y-intercept, K _M can be computed as the slope/Y-intercept. Because from Equation 21.12 the X-intercept is –1/K _M , K _M can also be computed directly from this relationship. K _M can be computed directly from the Michaelis-Menten equation ( Eq. 21.10 ) from V _max . When [S] = K _M , from Equation 21.10 , v ₀ = V _max /2. Thus, the K _M is the substrate concentration necessary to reach V _max /2. A typical Lineweaver-Burk plot is shown in Figure 21.5 .

Figure 21.5, A typical Lineweaver-Burk (1/v o vs. 1/[S]) plot, from Equation 21.12 , for an enzyme-catalyzed reaction. v 0 is the initial velocity of the reaction at time t = 0, where the substrate concentration, [S], is known. The figure shows that [S] must cover a range from where it is significantly less than K M (0.5 K M ) to where it is significantly greater than K M (5 K M ) to obtain reliable values for K M and V max . The Y-intercept is 1/V max , and the X-intercept is –1/K M . The slope is K M /V max .

Practically, after the points are obtained from the double reciprocal plot, the least squares best line is drawn through the points from which the slope and X- and Y-intercepts are directly determined. The correlation coefficient, which is a measure of the closeness of fit of the experimental points to the best line, is also calculated and should be greater than 0.9, that is, a high correlation.

Note in the above procedure and as is illustrated in Figure 21.5 that substrate concentrations must span a range that brackets K _M . Measurements of v ₀ at low [S] have relatively large errors, as illustrated in the upper-right portion of the line in Figure 21.5 , yet it is these estimates that are critical in determining accurate values of K _M and V _max . Modern computer programs provide reasonably accurate values for K _M and V _max based on weighted values of the initial velocities. Weights are assigned based on the magnitude of v ₀ . In addition, other computer programs use nonlinear regression analysis to fit the weighted data to a hyperbolic v ₀ versus [S] curve, as in Equation 21.10 , and a Lineweaver-Burk plot is used only for visual display of the kinetic data.

Once K _M is known, saturating concentrations of substrate can be used such that [S] > > K _M . Thus, for example, if K _M = 1 × 10 ^–5 M for a certain enzyme for which an assay is desired, we can use a substrate concentration of 1 × 10 ^–3 M (1 mM) and be assured that [S] > > K _M , here by a factor of 100, so that Equation 21.11 applies. The substrate at this concentration is added to a patient sample (most often, serum), and the rate is observed and then divided by k ₂ to obtain the total concentration of enzyme. As discussed later, because many enzymes exist as different isozymes with different k ₂ and K _M values, division by k ₂ is not performed and the results are reported directly as k ₂ E _T , referred to as total activity units.

A Word About K _M

Equation 21.1 shows that the ES complex is in equilibrium with free E and free S. We can write an equilibrium constant for this process as a dissociation constant, K _s , as k ₋₁ /k ₁ , which is equal to [E][S]/[ES]. The reciprocal of this constant, or the association constant, K _A , is k ₁ /k ₋₁ = [ES]/[E][S]. From Equation 21.5 , K _M is defined as (k ₋₁ + k ₂ )/k ₁ . Note that when k ₋₁ > > k ₂ , K _M is the same as K _S . This condition actually pertains to most enzyme-catalyzed reactions; k ₋₁ is the rate of dissociation for the enzyme-substrate complex that almost always involves the breaking of noncovalent bonds, and k ₂ is the rate for the breaking and/or making of covalent bonds. Usually, the energy necessary for the former process is much less than for the latter; therefore, the rate of dissociation, k ₋₁ , of the noncovalent ES complex is higher than the rate, k ₂ , for the covalent catalysis step. Thus, K _M is the dissociation constant for the ES complex. The reciprocal of this is K _A , the association constant, and it is the affinity of the substrate for the enzyme.

However, in some cases, the rate for the covalent catalytic step is greatly enhanced. Examples include carbonic anhydrase (k ₂ = 10 ⁶ sec ^–1 ; carbon dioxide is the substrate) and catalase (k ₂ = 10 ⁷ sec ^–1 ; hydrogen peroxide is the substrate). For these enzymes, because k ₂ is large, K _M is not a dissociation constant but rather a steady-state constant, equal to k ₂ /k ₁ .

Enzyme Activity

As noted previously, computation of total enzyme concentration using Equation 21.11 is often not performed because many enzymes have multiple isozymes. For example, at least five isozymes of LD are known, each having a different set of values for K _M and k ₂ . In this case, the total enzyme activity of LD is given, that is, k ₂ × [E _T ]. In these cases, enzyme activities are all reported in units called international units , defined originally in 1964 by the International Commission on Enzymes. One international unit (IU) is the amount of enzyme that catalyzes the formation of one micromole of product (or the disappearance of 1 micromole of substrate) in 1 minute. It applies only under specified conditions of pH, temperature, and ionic strength, all factors that influence enzyme activity, as discussed later.

With development of the Système International d’Unités system and the use of moles and seconds as base units, a second definition for the unit of enzyme activity was developed, the katal: 1 katal is defined as the amount of enzyme that catalyzes the conversion of 1 mol of substrate to product in 1 second under the conditions used in the assay. One IU is equal to 16.7 nanokatal (nkat), and 1 katal is equal to 6 × 10 ⁷ IU. Both definitions unfortunately omit volume. Generally, 1 IU is reported per liter (L); the right side of Equation 21.11 has the units of concentration per time so that IU/L conforms to these units. It is vital that, if total enzyme activity is reported, the substrate used in the assay for the enzyme also be reported because the k ₂ value differs for different substrates.

As discussed later, many factors affect enzymatic activity, including pH, temperature, ionic strength, concentration of cofactors of an enzyme, presence of inhibitors, use of other enzyme reactions as indicators, and whether the forward or backward reaction is used to measure the enzyme concentration. For example, LD measured using the forward reaction has approximately one-third the activity of LD measured using the reverse reaction, and lipase measured with colipase present has 5 to 10 times the activity of lipase measured without its cofactor.

Therefore, even if the same substrate is used by different laboratories, the reference ranges of enzymes may differ dramatically among these laboratories. Furthermore, differences in reference ranges between two different laboratories can still exist even if the above factors are the same for both, because of different assay conditions.

To attempt to standardize enzyme activities, one approach is to have each laboratory set the upper boundary of the reference range to 100 ( ). Then all other values are expressed as percentages or ratios. A result indicating that an enzyme level was 10 times normal is useful to a physician. If the result is 10X U/L, then the physician must hunt the value of X and calculate the ratio. As long as the assays are performed with internal consistency in a highly reproducible manner, quantitative results are comparable between one laboratory and another if relative activities are reported. More commonly, the results of enzyme assays are now expressed in IU along with the reference ranges for each enzyme, allowing for evaluation of the patient’s condition, progression of disease, or efficacy of therapy.

Measuring Enzyme Activity

In principle, in the measurement of enzyme activity, either the rate of disappearance of substrate or the rate of appearance of product can be measured. In general, it is easier to measure small increases in product than to measure small decreases in a relatively high concentration of substrate often needed to achieve saturation. As discussed previously, to measure enzyme activity in a sample, it is most common to use substrates at saturating concentrations where zero-order kinetics with respect to [S] occur. Under these conditions, the reaction rate is directly proportional to the total amount of enzyme present.

Equation 21.11 states that, at saturation, the rate of product formation with time is constant. This implies that the concentration of product increases linearly with time. Experimentally, P is determined at different time points, and a least-squares best-fit line through the points is determined. If the correlation coefficient is high, [P] increases linearly with t, confirming saturation of the enzyme by substrate. The slope of this line is V _max , which may be reported directly as activity or divided by k ₂ to give enzyme concentration.

The most common cause of a nonlinear relationship between P and t is the presence of an inhibitor that will be discussed later. In cases such as these, dilution of the serum or other body fluid sample is warranted because this will dilute the concentration of the inhibitor, although it will also dilute the total enzyme concentration. However, as long as [S] is present at saturating conditions and [P] can be measured, valid total enzyme concentrations or activities can be measured.

Typically, in enzyme assays, a lag phase follows mixture of the specimen and reagents when preliminary reactions and mixing of sample occur. The initial absorbance of the sample is based on the absorbance due to the reagents and the sample and is considered to be zero in terms of making an interpretation of enzyme activity. Once the reaction begins, the graph will follow a straight line for a period of time. At this point, the reaction is zero-order and enzyme activity can be determined. If the reaction is allowed to proceed, substrate is consumed and [S] falls toward K _M . If [S] falls substantially below K _M , the reaction will then be first-order, and v ₀ will be affected both by the amount of substrate (which is not a constant) and by the enzyme activity.

Spectrophotometric Assays

In most cases, enzyme activity is measured spectrophotometrically. In addition, other detection methods are used as appropriate, depending on the product being measured. For example, lipase acts on emulsions of lipid; these are often turbid so that measurement of the rate of clearance of turbidity could be used to determine lipase activity. Glucose oxidase, widely used to measure glucose concentration, is a flavoprotein that uses oxygen as an electron acceptor. The change in potential due to alteration in charge on the acceptor can be measured to determine the reaction rate. Urease is widely used to measure urea concentration; urease splits urea into bicarbonate and ammonium ions. The change in conductance of the specimen due to the appearance of the ions in the sample can be used to determine the rate of reaction.

Because assay methods based on spectrophotometry are the most common, we will focus on these in describing how enzyme assays are performed. In the simplest case, the substrate does not absorb light at a particular wavelength at which the product absorbs strongly. An excellent example of this is LD, which catalyzes reversibly the oxidation of lactate to pyruvate. Because lactate is a unique substrate for LD, it is preferred. Pyruvate can be used as the substrate, except that it is also the substrate for several other enzymes such as pyruvate dehydrogenase and ALT, among others.

When lactate is oxidized to pyruvate, the cofactor, NAD ⁺ , becomes reduced to NADH. For each mole of lactate oxidized to pyruvate, 1 mole of NADH forms. NADH absorbs strongly at 340 nm; NAD ⁺ does not absorb light at this wavelength. Therefore, the addition of saturating concentrations of both lactate and NAD ⁺ to a patient’s serum will result in a linear increase in absorbance at 340 nm over a given period, from which total enzyme activity is directly determined as described earlier. In this case, the increase in concentration of NADH, ΔP, over the time period, Δt, is proportional to the increase in absorbance, ΔA, at 340 nm, by Beer’s law, as described in Chapter 4 , that is,

ΔP/Δt=ε× (ΔA/Δt) ×L

$ΔP/Δt=ε× (ΔA/Δt) ×L$

L in Equation 21.13 is the path length of the reaction vessel or cuvette, almost always equal to 1 cm. ε is a proportionality constant (most often, the molar extinction coefficient) in Beer’s law, which is 6.22 × 10 ³ L mol ^–1 cm ^–1 for NADH at 340 nm. On most current chemistry analyzers, a volume of a patient’s serum sample is added to the reaction cuvette containing the reaction components (lactate and NAD ⁺ ), and ΔA is observed. This results in dilution of the volume (Vp) of the patient’s serum to the total volume of the reaction mixture (Vo), so that

Enzyme activity=ΔP/Δt=ε× (ΔA/Δt) ×L (V_{0} / V_{P})

$Enzyme activity=ΔP/Δt=ε× (ΔA/Δt) ×L (V_{0} / V_{P})$

One caveat in the previous assay is that LD also catalyzes the reverse reaction (i.e., pyruvate to lactate). Therefore, as pyruvate forms, it can serve as an end-product competitive inhibitor (see the Inhibition of Enzymes section later in the chapter) and can drive the reaction back to lactate. Therefore, it is important to be able to take the measurements in Equation 21.14 over a short time before pyruvate builds up to significant levels.

Coupled Enzymatic Reactions

In many instances, however, neither the product nor the substrate of a chemical reaction can be measured conveniently. In such instances, the enzymatic reaction can be “coupled” to another reaction that uses the product of the enzyme-catalyzed reaction to produce an indicator substance. An example of a typical coupled enzymatic reaction is the Oliver-Rosalki method for measurement of CK activity, illustrated in Equations 21.15 through 21.17 , later. The reverse reaction of CK is used, producing adenosine triphosphate (ATP), which is used in a second reaction to produce glucose-6-phosphate (G6P) from glucose + ATP. The third reaction in the sequence results in the reduction of nicotinamide adenine dinucleotide phosphate, or NADP ⁺ , to NADPH, the indicator of the reaction. In these coupled reactions, it is critical that the rate-limiting step in the overall reaction is the CK-mediated step that generates ATP. This can be achieved by using high concentrations of the indicator enzymes to ensure rapid conversion of the substrates of the subsequent reactions.

One potential problem with CK measurements when this reaction scheme is used is the presence of other enzymes that can generate ATP. Adenylate kinase, an enzyme found in red blood cells and liver, converts adenosine diphosphate (ADP) to ATP (see Eq. 21.34 ); specimens with high adenylate kinase activity will have falsely elevated values for CK activity.

Creatine phosphate + ADP → Creatine + ATP (catalyzed by CK)

Glucose + ATP → G6P + ADP (catalyzed by hexokinase)

G6P + NADP ⁺ → 6 - Phosphogluconate + NADPH (catalyzed by glucose -6- phosphate dehydrogenase, or G6PD)

Complication:

2 ADP → ATP + AMP (catalyzed by adenylate kinase)

The absorbance increase at 340 nm due to NADPH is proportional to the [ATP] generated as the end-product of the CK reaction, as expressed in Equation 21.15 .

In assays of enzyme activity, some methods use endpoint measurements, discussed in Chapter 28 , determining the concentration of substrate or product at a specific time after addition of the sample. Endpoint methods are typically used in simple methods, such as bedside glucose testing or dipstick reactions, as for glucose or leukocyte esterase in urine. Endpoint methods may give erroneously low results in situations in which enzyme activity is very high. Most enzymatic assays use kinetic methods of measurement (as discussed earlier), whereby the rate of change in concentration of substrate or product is determined. (For the sake of simplicity, throughout the rest of this section, only measurement systems that detect appearance of product will be described. The same principles, however, would apply to situations in which rate of disappearance of substrate is being monitored.) Kinetic methods are more accurate and make it easier to detect changes in reaction conditions and samples requiring dilution. In a time-course study, the rate of reaction can be expressed as ΔP/Δt, the change in amount of product per unit time. Because the IU and the katal represent the amount of enzyme producing a specific amount of product in a given time period, this approach allows direct reporting of enzyme activity in either IU or katal, as desired.

Enzyme Assays Under Nonsaturating Conditions: First-Order Rate Processes

As discussed later, there are circumstances under which it may not be possible to perform an enzyme assay under saturating conditions in which Equation 21.11 applies. In these circumstances, assay conditions may be used in which S < K _M . The Michaelis-Menten equation (21.10) then becomes

V_{0} =d [p] /dt= K_{2} E_{T} \cdot [S] / K_{M}

$V_{0} =d [p] /dt= K_{2} E_{T} \cdot [S] / K_{M}$

Because E _T is constant, the initial rate of the reaction depends only on the concentration of S. When S decreases, ES and P increase so that –d[S]/dt = d[ES]/dt + d[P]/dt. But, under the reaction condition that [S] > > [E], the steady-state assumption, d[ES]/dt = 0, is valid. Therefore, the rate of product formation equals the rate of substrate depletion, that is,

V_{0} =d [p] /dt=- [S] d/dt= K_{2} E_{T} \cdot [S] / K_{M}

$V_{0} =d [p] /dt=- [S] d/dt= K_{2} E_{T} \cdot [S] / K_{M}$

This is the equation for a first-order process, that is, the rate depends only on the concentration of a single species, in this case the substrate. Because the rate also formally depends on E _T , it is properly called a second-order reaction. However, in this case, E _T is constant and does not change during the reaction. It is therefore referred to as a pseudo–first-order reaction. E _T can be determined from determination of the initial rate of the reaction in which the initial substrate concentration, S ₀ , is known. Because K _M and k ₂ are known,

E_{T} = (V_{0} / [S_{0}]) \times (K_{M} / K_{2})

$E_{T} = (V_{0} / [S_{0}]) \times (K_{M} / K_{2})$

If only total enzyme activity is to be reported, then v ₀ /S ₀ , which is equal to (k ₂ /K _M )[E _T ], is reported because this quantity is directly proportional to E _T . Note, though, that these are not the same activity units as are used under saturating conditions because the total enzyme concentration in that case is multiplied only by k ₂ and, in the current circumstance, it is multiplied by k ₂ /K _M because of the fact that saturation has not occurred.

Another approach to determination of E _T under nonsaturating conditions is to integrate Equation 21.20 for S in terms of t. This results in the following relationship:

\ln ([S] / [S_{0}]) =2 .303log ([S] / [S_{0}]) =- (K_{2} K_{T} / K_{M}) \cdot t

$\ln ([S] / [S_{0}]) =2 .303log ([S] / [S_{0}]) =- (K_{2} K_{T} / K_{M}) \cdot t$

where ln is the natural logarithm to the base e and [S ₀ ] is the initial substrate concentration. If the substrate concentration is determined at specific times, a plot of the log (S/S ₀ ) versus time should give a straight line whose slope is –(k ₂ E _T /K _M )/2.303. Because both k ₂ and K _M are known, E _T can be directly evaluated. This method eliminates the need to measure initial velocities involving small changes in [S]. This method is advantageous when the substrate solubility does not permit saturating substrate concentrations to be reached.

The above first-order rate equation is the general equation for all first-order rate processes that abound in biology. Many reactions in the body occur either by first-order processes or by pseudo–first-order processes in which the rate depends only on the concentration of one species. As discussed in Chapter 24 , when drugs are administered to the body, they decay very often by a first-order process, where the rate of disappearance of the drug depends only on the concentration of the drug. One important feature of this process is the so-called half-time . Note, from Equation 21.22 , that the half-time, t _1/2 , or the time required for half of S ₀ to be consumed, that is, when [S] = [S ₀ ]/2, is a constant that depends only on the rate constant in the equation. The nondependence of t _1/2 on concentration is a cardinal feature of first-order rate processes.

Because log (2) = 0.3, the above equation reduces to

t_{1/2} =0 .69/K

$t_{1/2} =0 .69/K$

where, in this case, k = K _M /k ₂ E _T and t _1/2 is the half-time, that is, the time required for half of the substrate to be consumed. Thus, if the half-time for substrate consumption is known, E _T can also be directly computed from Equation 21.23 provided that K _M and k ₂ are known.

Other Factors Affecting Enzyme Activity

Temperature

Enzyme-catalyzed reaction rates are extremely sensitive to temperature changes; to ensure accuracy, the temperature of the reaction mixture must not deviate by more than ±0.1° C from the assigned temperature. In general, every 10° C increase in temperature leads to an approximate doubling of enzyme activity, although this varies slightly from one enzyme to another. The use of higher temperatures gives faster reaction rates and improves sensitivity—an advantage when enzyme activities are low. Lower temperatures increase the linear limit of an assay, requiring fewer dilutions. The choice of temperature with most modern instruments is governed by the capabilities of the instrument. There is a limit to the amount of temperature increase that can be used; most enzymes start to denature and become inactive as the temperature is increased. For example, CK starts to denature at 37° C, and amylase begins to denature at 45° C. On the other hand, some enzymes remain stable at extremely high temperatures. As an extreme case, the Taq polymerase used in the polymerase chain reaction is stable at 95° C. Taq polymerase and the polymerase chain reaction are discussed in Chapter 69 .

Another issue concerning thermal stabilities of clinically significant enzymes is the effect of low temperatures on their stabilities, that is, when samples are stored prior to reassay or to initial assay. In the former case, it is sometimes necessary to perform a reassay for an enzyme if the first result was questionable clinically. Normally, patient samples that have been assayed are stored at 4° C (refrigeration temperature) for about 1 week, after which time they are discarded. The question is whether the reassay result is reproducible in this 1-week time period. Some earlier studies suggested that ALP, ALT, AST, CK, but not LDH are stable in this time period ( ) while other studies found that ALP was not stable, especially in the presence of magnesium ions. On the other hand, recent studies suggest that the stabilities of ALP, ALT, AST, CK, and LDH are all reproducible (statistically identical) over this time period ( ). In the latter case, in which samples are stored frozen either at −20° C or −80° C (dry ice temperature) prior to assay, there is a recent study on the activities of salivary ALP, ALT, AST, and LDH that suggests that the activities of all of these enzyme decrease in a statistically significant manner over a 2-week period when stored at −20° C but not when stored at −80° C ( ). In contrast, the activities of the same enzymes and CK in serum were found to be statistically reproducible over a 1-month period except for ALT when stored at −20° C ( ). These results suggest that the medium (salivary fluid vs. serum) may be an important determinant of reproducibility and that storage of serum samples over 1 month at −20° C will yield reproducible results for these enzymes, except for ALT.

pH

Enzymes have a pH optimum for maximal activity; usually, the pH of the reaction conditions is chosen to be that at which the enzyme exhibits the greatest activity. Selection of pH is not always critical; some enzymes have a very broad pH maximum so that small changes in pH do not appreciably change activity. For example, ALP has maximum activity at pH values between 9 and 10. In some cases, particularly for enzymes with multiple isoenzymes, selection of pH represents a compromise, as different isoenzymes may have maximum activity at differing pH values. In this situation, the pH for the reaction is selected to allow measurement of the activities of all isozymes.

Salt and Protein Concentrations

The ionic strength of solutions affects enzyme activity; if ionic strength is too high, enzyme activity drops. The activity of many enzymes is also affected by protein concentration. When enzyme activity is over the linear limits of the assay, dilution of plasma typically requires use of enzyme diluents containing plasma proteins. Human plasma contains about 70 g protein/L, but normal urine has almost no protein; use of proteins such as albumin increases the activity of urinary amylase and standardizes its measurement. In protein-free solutions, enzymes lose activity rapidly either by denaturation or by adsorption to the walls of the container.

Inhibitors and Interferences

Typically, enzymes are measured in serum samples. Heparinized plasma is generally considered an equivalent sample to serum for most routine analytes; however, this may not be the case for enzymes. Heparin may inhibit the activity of some enzymes—notably, amylase and AST (using some, but not all, methods). Citrate, used in evacuated collection tubes for coagulation testing and as a preservative in blood products, complexes divalent cations, among which calcium ion is most prominent. Citrate-containing specimens may cause falsely low results for enzymes such as CK and ALP. Ethylenediaminetetraacetic acid (EDTA) and fluoride inhibit the activity of many enzymes and should almost never be used for specimens for enzyme analysis. An exception is in measurement of renin, in which EDTA inhibits the action of enzymes that convert prorenin to the active enzyme renin and prevents artifactual increase in renin activity.

Caveats In Enzyme Assays

Some of the causes of errors in enzyme assays, such as the presence of inhibitors, have been mentioned previously. Here, we summarize the most common problems that can be encountered.

K _M -Type Mutations

In certain deficiency states, the conditions of the in vitro assay may not mirror the in vivo conditions that give rise to the deficiency state. In cases in which a genetic defect does not alter normal protein levels of enzyme and the k _cat value is unchanged, by applying the principle that the assay should be carried out at saturating substrate concentration, it is possible that a K _M -type mutation may go undetected. This is due to the fact that the enzyme, inactive at low substrate levels, exhibits full or nearly full activity at the higher [S] used in the assay. For example, a variant erythrocyte hypoxanthine-guanine-phosphoribosyltransferase is inactive in assays at low [S], but full activity is restored by increasing the substrate concentration. To guard against such a false positive, a clinical evaluation should include a determination of the K _M for the mutant enzyme.

One technique that can be employed to detect enzyme mutations that affect activity is the use of monoclonal antibodies directed against the enzyme of interest. Immunoassays for enzymes are discussed later. Correspondence between measurement of enzyme activity and the protein (enzyme) concentration from immunoassays will pertain as long as the enzyme antigen is fully active. Such is not always the case when inherited deficiencies associated with point mutations are involved. In these instances, estimates of enzyme concentration based on immunoassays can exceed those based on measurements of enzyme activity, indicating a defect in the enzyme. If the underlying basis of disease is genetic, it is best to estimate enzyme activity from kinetic measurements and compare these with normal values. Some mutations destabilize protein structure, leading to rapid intracellular proteolysis of the enzyme. In this instance, the results derived from immunologic methods and enzyme activity measurements can concur. The presence of inhibitors in the source biological fluid may lead to underestimation of the amount of enzyme present based on activity but not immunologic measurements. Usually, reversible enzyme inhibitors will not interfere with immunologic estimates of enzyme concentration.

You're Reading a Preview

Become a Clinical Tree membership for Full access and enjoy Unlimited articles

Become membership

If you are a member. Log in here

Key Points

General Properties of Enzymes

Catalysis

Enzyme Specificity

Enzyme Concentration And Activity

Molecular Basis For Enzyme Catalysis

Nomenclature of Enzymes

Isozymes

Enzyme Cofactors

Factors Affecting Plasma Enzyme Activities

Factors Affecting the Lifetime Of Enzymes In Blood

Enzyme Kinetics: Determination Of Total Enzyme Concentrations In Serum And Other Body Fluids

Determination Of Total Enzyme Concentration In Serum And Other Body Fluids By Michaelis-Menten Equation

Derivation of the Michaelis-Menten Equation

Total Enzyme Concentration Can Be Determined from the Initial Rate at Saturation

Knowledge of k 2 and K M Allows Determination of [S] Values That Will Saturate the Enzyme

The Lineweaver-Burk Plot Gives k 2 and K M

A Word About K M

Enzyme Activity

Measuring Enzyme Activity

Spectrophotometric Assays

Coupled Enzymatic Reactions

Enzyme Assays Under Nonsaturating Conditions: First-Order Rate Processes

Other Factors Affecting Enzyme Activity

Temperature

pH

Salt and Protein Concentrations

Inhibitors and Interferences

Caveats In Enzyme Assays

K M -Type Mutations

You're Reading a Preview

Related Posts

Guidelines for Ordering Blood for Elective Surgery

Disease/Organ Panels

Common Chimeric Genes Identified in Human Malignancies

SI Units

Knowledge of k ₂ and K _M Allows Determination of [S] Values That Will Saturate the Enzyme

The Lineweaver-Burk Plot Gives k ₂ and K _M

A Word About K _M

K _M -Type Mutations