Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Many doctors often equate statistics with the numbers and equations seen in research papers, but the term ‘statistics’ does not mean ‘numbers’; indeed, a competent statistical analysis of a paper should include non-numerical issues such as the nature of the sampling methods or the validity of a ‘gold standard’ diagnostic test. Furthermore, papers may be overflowing with numerical data but contain no statistics at all.
Statistics has been defined as the discipline concer-ned with:
Data collection and presentation
Inference from samples or experiments to the population at large
Modelling and analysis of complex systems
Broader issues to do with the application and interpretation of the above techniques in politics, management, the law, philosophy, ethics and the sciences.
One of the problems in getting to grips with statistics is that, in common with many other branches of medicine, it is becoming an increasingly sophisticated science, where standard textbooks appear to serve only those who are already members of its exclusive club. The analysis of large and complex datasets, and the techniques of mathematical modelling and statistical computer programming, are generally best left to the experts. However, the appraisal of many published articles relevant to the practicing obstetrician or gynaecologist can be greatly helped by an understanding of several basic principles, some of which are presented in this chapter.
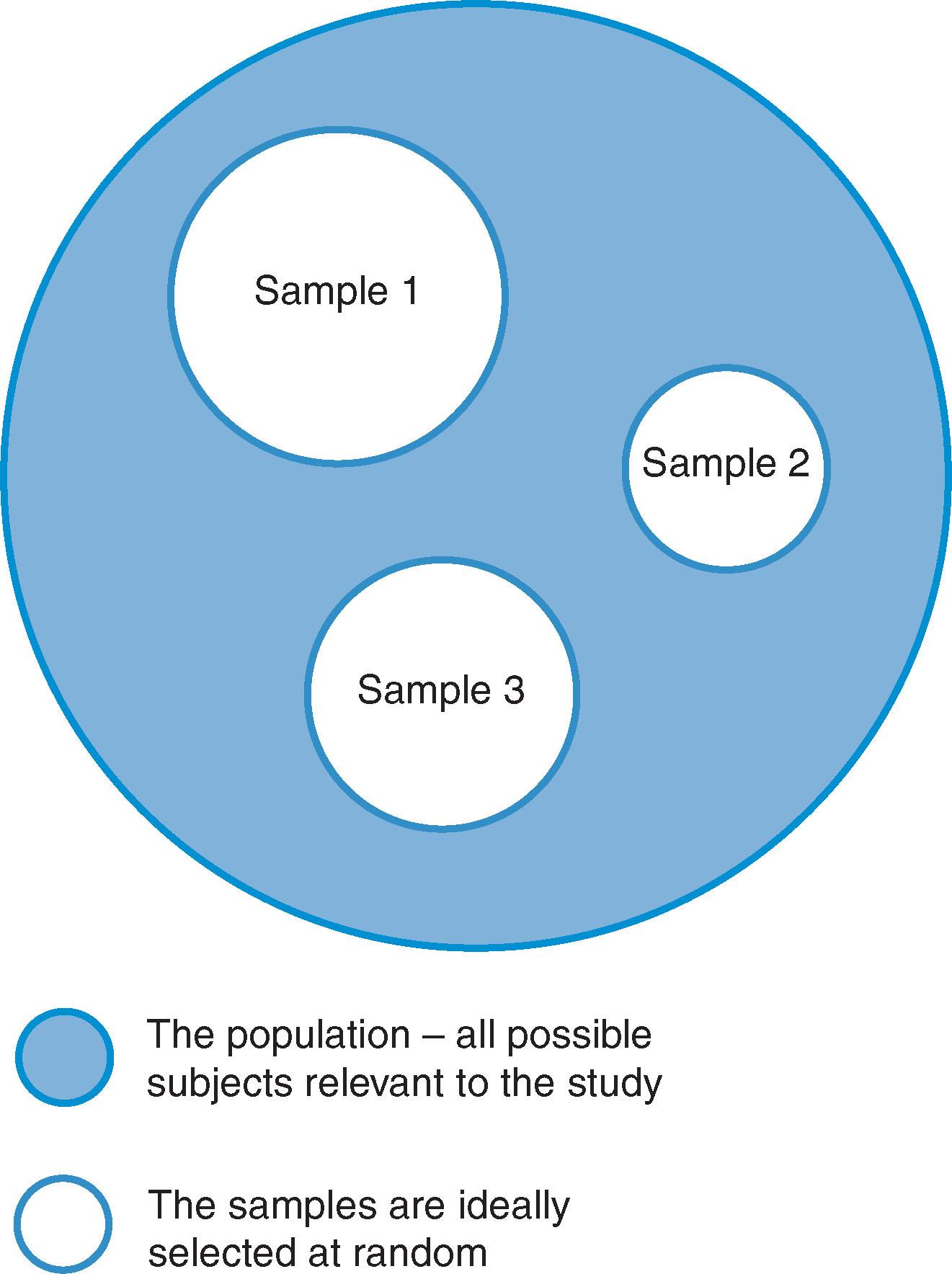
The most fundamental issue of statistics is that one is trying to relate data taken from a relatively small ‘sample’ to a much larger group where it would be impractical to collect all the available data. In medical statistics, this large and rather nebulous group of subjects is known as ‘the population’ and it can often be hard to define. This may seem obvious but understanding the concept of sampling is crucial in the interpretation of results from studies. The application of statistics to research is an attempt to ensure that the results from your sample are in general agreement with the results that would have occurred if you had been able to conduct the experiment on all relevant members of the population in question. Fig. 14.1 demonstrates this simple relationship, and it is intuitive to see that, as the sample size increases, it moves closer to representing the population. In general, as the size of the sample increases, the bias in the study decreases; however, this is not always the case, and in some unusual statistical settings the bias will remain, but these are beyond the scope of this chapter (see Peacock and Peacock, 2011).
The most important ‘take-home’ message for you as an investigator is that, if you repeated your experiment, you would almost certainly get a different result. You may still draw the same conclusions from that result, but the numbers used in the statistical calculations would differ from sample to sample. On average, you would expect the results to be consistent, but when there is disagreement between sample and population, the following types of error (Type 1 and Type 2 errors) can occur and these should always be at the front of your mind when interpreting study results.
This occurs when ‘the sample’ used in your experiment generates a significant result for your hypothesis but there would not have been a significant result if you had performed the experiment on ‘the population’; in other words, it occurred by chance. When we set a ‘significant’ P value at .05, we are allowing a 5% chance of a type 1 error occurring for our study. To have zero chance of a type 1 error we would need to perform the experiment on ‘the population’ itself, and this is not possible as it implies recruiting an infinite number of subjects. The 5% level is entirely arbitrary and purely a convention that seems ‘reasonable’ in most research situations. Thus, P values should be interpreted cautiously, always bearing in mind the study design and the size of the difference observed between the comparative groups. P values are a continuum that runs from 0 to 1 and thresholds such as .05 are only used as a guide. On occasions, different levels are used, such as 1% ( P value of .01) and 10% ( P value of .10).
Another consideration when interpreting the results of a study is whether many comparisons have been made using the same sample. This is known as ‘multiple testing’ and it is a common flaw seen in a number of studies in the published literature (see Peacock and Peacock 2011 for further details on how to address this). By setting your P value for significance at .05, you are allowing a 5% chance of a type 1 error, that is, 1 in 20 statistical comparisons will produce a significant result by chance and thus, if a large number of variables in the dataset are tested for significance, there is a considerable risk of getting a type 1 error. Multiple testing often goes hand in hand with an unclear hypothesis and a poorly thought through study design. If you wish to test many outcomes and exposures using the same sample of patients, you need to account for this by setting yourself a more stringent P value for significance, for example, .01. In this case, you would need to make 100 comparisons in order for one of them to be significant by chance.
This occurs when ‘the sample’ used in your experiment fails to generate a significant result for your hypothesis but there would have been a significant result if you had performed the experiment on ‘the population’, that is, you have missed a real and possibly important effect. When we require a study to have 90% power, we are allowing a 10% chance that our sample will not detect a significant result that in truth exists in the population. This commonly occurs in small studies where there is insufficient power. Under-powered studies can be frustrating to interpret, particularly when there appears to be quite a large difference between the groups but the P value does not reach the magical threshold for acceptance as a significant result. Some statisticians argue that no under-powered studies should ever be undertaken as they cannot be interpreted and can raise ethical concerns in terms of unjustified patient research, and this would probably condense the world’s research output to a fraction of its current amount. Most research funders now demand power calculations, but sometimes the assumptions on which power calculations are based are grossly optimistic. However, in many cases a balance can still be achieved between attaining sufficient power and setting a pragmatic target for the sample size.
It is always important to be able to define the null and active hypotheses for a study, and this means having clear definitions for both the outcome and the exposure or treatment. Under the null hypothesis, there is no difference between the groups that are being compared. This will tend to be the ‘default’ hypothesis unless the study sample accrues sufficient evidence to reject this null hypothesis and show that the active hypothesis is true.
When studies have been sampled in a non-random fashion, differences between the results from the sample and the true population can arise. Similarly, if treatments are allocated to patients non-randomly, estimates for differences between treatment groups can be biased. In other words, bias can arise if the sample is systematically unrepresentative of the population. However, bias and generalisability are not always the same thing. If one runs a well-powered randomised controlled trial (RCT), the results comparing randomised groups that are estimated from the sample are unlikely to be biased; however, they will only be generalisable to the sub-group of the population that met the inclusion criteria for the study. Thus, when interpreting the results from studies it is important to view them in relation to the study inclusion and exclusion criteria and the sampling methods that were employed when recruiting the subjects. There are many different types of bias and certain study designs are more prone to particular types of bias than others. This will be discussed in more depth in the section about types of study and experimental design ( pp 10 ).
When interpreting a result from a sample, it is useful to express the result with a range of possible values that it might have taken if other samples of the same size had been selected. This range of values is called a confidence interval (CI), and we can set the level of confidence as a percentage; 95% confidence is typically used. For example, if we measure the birth weight of 50 babies and calculate a point estimate for the mean weight of 3360 g and a 95% CI of 3200 to 3520 g, this means that we can be 95% confident that, given this sample size, the true mean birth weight for all babies in the population relevant to this study lies somewhere between 3200 and 3520 g. In general, as the sample size increases, the CI becomes narrower. The term precision is used to describe how wide the CI is around the point estimate, whereas accuracy gives an indication of how close the point estimate from the sample is to the true unmeasurable population value and is therefore more related to bias or generalisability. The calculation of CIs will be discussed in more detail on p. 7 .
When designing a study, there will often be many research outcomes listed. In general, one or a few of these outcomes will be identified as the primary outcome(s). The primary outcome(s) is used to calculate the sample size for the overall study. A well-presented study will provide the P value along with the CI of the primary outcome(s) being measured, while the estimates of the secondary outcomes should be reported with CIs.
Many statistical tests make assumptions about the independence of the subjects analysed in the study. If data are not independent (e.g. the same mother can be included more than once in a study on childbirth) then account should be taken of this in the analysis. Many commonly used statistical tests assume that all observations are from separate individuals and, by including subjects more than once, you are making your sample less varied than it would be if subjects were only entered once. Similarly, if your study design selected cases and controls by matching them in terms of covariates such as age and ethnic group, then your analysis must account for this matching. In general, it is preferable not to match any subjects within a study as it is possible to adjust for potential differences between your groups at the analysis stage. Furthermore, in studies where subjects have been assessed before and after experiencing an exposure, they should be investigated in a ‘paired’ fashion by analysing the difference between the before and after measurements, as this accounts for the lack of independence between them. This also tends to improve the power of the study as within-patient differences tend to be less variable than absolute variation between patients.
There are many different ways in which we can collate data on a subject of interest but, in general, data can be classified into the following types:
Quantitative or continuous – a continual spectrum of data measurements, for example, age, blood pressure, height or weight.
Ordinal – subjects are categorised into groups where there is some order to the categories, for example, mild, moderate or severe symptoms.
Categorical – subjects are categorised into groups but there is not necessarily any particular order to the categories, for example, ethnicity or country of birth.
Binary – this is a sub-group of ordinal and categorical data where there are just two possible categories, for example, pregnant or not pregnant, dead or alive.
Time-dependent data – where subjects have been followed up for different lengths of time, typically in cohort studies and RCTs when subjects have been recruited over an extended period of time. For example, the classification of a subject as pregnant or not pregnant may depend upon the length of their follow-up.
When analysing these data types, it is often necessary to make assumptions about how the data within our sample are likely to behave in relation to the population from which they came. In order to do this, it is helpful to assume a probability distribution which can be described by a mathematical equation, and this can then be used as a template to describe the sample data and make comparisons within it. There are many types of mathematical distribution used in statistics, but four of the most common ones are the binomial, Poisson, normal and chi-squared (χ 2 ) distributions:
The binomial distribution describes the probability distribution for binary data, and it relates to the common example of tossing a coin. For large sample sizes, the binomial distribution is very similar to the normal distribution and so the latter is often assumed in the statistical calculations.
The Poisson distribution can be assumed when investigating rates derived from time-to-event data, and it represents the idea that a certain event is occurring at a constant rate and thus, as we follow people through time, more events will occur. However, it should be noted that there are also more complex assumptions that are required when analysing time-to-event data, for example, Cox proportional hazards regression analysis is often used (see Peacock and Peacock, 2011).
The normal or Gaussian distribution is assumed when investigating measurements from continuous data, but it is also used as the basis for many aspects of medical statistics. More detail is provided for this distribution a little further on, as it is so important in understanding the application of statistics.
The chi-squared ( χ 2 ) distribution is derived by squaring the normal distribution, and it has particular properties that make it useful for investigating proportions from categorical, ordinal or binary data.
The normal distribution is one of the most important and widely used probability distributions in medical statistics. It can be described by a rather complex mathematical equation; however, if it is plotted in terms of probability, we can see that it generates the famous ‘bell-shaped’ curve shown in Fig. 14.2 . The x-axis is standardised such that the mean corresponds to zero (the most probable value) with units of standard deviation (SD) falling above and below this value. It can be seen that 95% of the area under the curve lies between the points that fall 1.96 SDs on either side of the mean value, and this number is particularly important as we can use it to give us an indicator of the range of values that would incorporate 95% of all possible values. In some cases, you may wish to know the range of values that incorporate 90% or even 99% of all values, and these ranges correspond to the 1.65 and 2.58 SDs on either side of the mean, respectively.
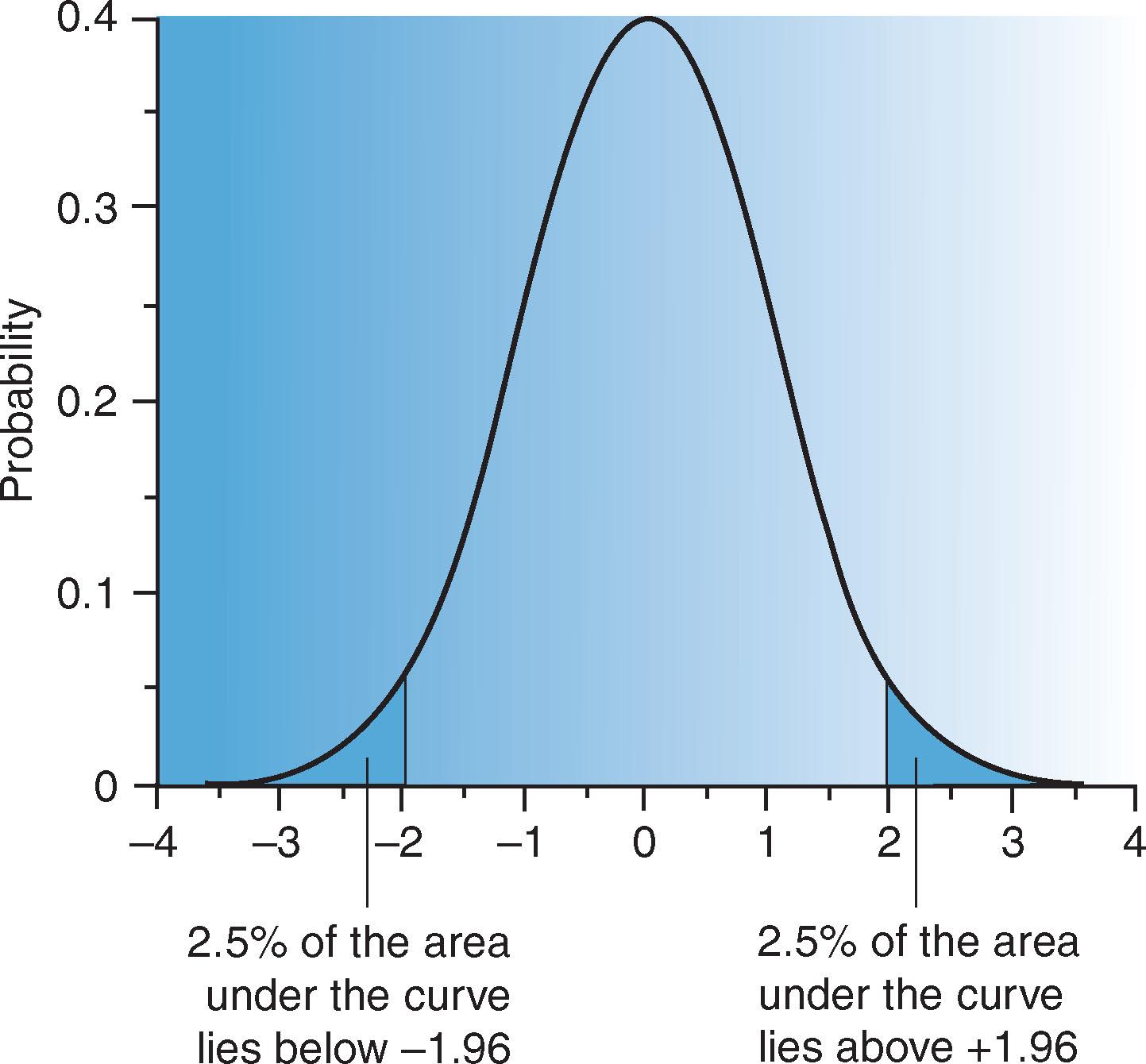
The beauty of the normal distribution is that this symmetrical property around the mean value holds whether we are plotting the actual data points from our sample or whether we are plotting the results of the study if we had repeated it over and over again. In this scenario, we would end up with the ‘mean of the mean of the samples’, and the range of mean values can be represented by the sampling distribution. The term standard error is essentially the SD of this sampling distribution and it is used throughout statistics to calculate CIs around point estimates. An example of how to calculate a CI for the mean is given on p. 7 .
Parametric statistical tests are ones where assumptions are made about which mathematical distribution best represents the sample and the population from which it was taken. Non-parametric statistical tests are ones where no assumption has been made about the distribution of the data. See Table 14.1 ‘A guide to unifactorial statistical methods’. In general, parametric tests tend to be more powerful and sensitive than non-parametric tests and therefore tend to be preferred, as fewer observations are required to provide evidence in favour of the hypothesis if it is true. A typical example of a parametric test is the use of a Student’s t -test to compare the mean values of a continuous variable between two groups. One of the test assumptions is that the continuous data measured in the sample can be assumed to follow the normal distribution. If this assumption is not valid, then the non-parametric Mann–Whitney U test can be used, which ranks the observations in order of size and compares the proportions that fall above and below the median value for each of the groups in question. Thus, the Mann–Whitney U test is less sensitive to large outlying values but also less informative as observations above or below the median are all treated in the same way.
| Design or Aim of Study | Type of Data/Assumptions | Statistical Method |
|---|---|---|
| Compare Two Independent Samples | ||
| Compare two means | Continuous, Normal distribution, same variance | t test for two independent means |
| Compare two proportions | Categorical, two categories, all expected values greater than 5 | Chi-squared test |
| Compare two proportions | Categorical, two categories, some expected values less than 5 | Fisher’s exact test |
| Compare distributions | Ordinal | Wilcoxin two-sample signed rank test equivalent to Mann Whitney U test |
| Compare time to an event (e.g. survival) in two groups | Continuous | Logrank test |
| Compare Several Independent Samples | ||
| Compare several means | Continuous, Normal distribution, same variance | One-way analysis of variance |
| Compare time to an event (e.g. survival) in several groups | Continuous | Logrank test |
| Compare Differences in a Paired Sample | ||
| Test mean difference | Continuous, Normal distribution for differences | t test for two paired (matched) means |
| Compare two paired proportions | Categorical, two categories (binary) | McNemar’s test |
| Distribution of differences | Ordinal, symmetrical distribution | Wilcoxon matched pairs test |
| Distribution of differences | Ordinal | Sign test |
| Relationships Between Two Variables | ||
| Test strength of linear relations between two variables | Continuous, at least one has Normal distribution | Pearson’s correlation |
| Test strength of relationship between two variables | Ordinal | Spearman’s rank correlation, Kendall’s tau (if many ties) |
| Examine nature of linear relationship between two variables | Continuous, residuals from Normal distribution, constant variance | Simple linear regression |
| Test association between two categorical variables | Categorical, more than two categories for either or both variables, at least 80% of expected frequencies greater than 5 | Chi-squared test |
| Test for trend in proportions | Categorical, one variable has two categories and the other has several categories which are ordered, sample greater than 30 | Chi-squared test for trend |
For binary data, the assumption of a binomial distribution may be valid, as according to Peacock and Peacock, 2011, the normal distribution ‘can be used as an approximation to the Binomial distribution when n is large. In precise this works if np and n(1−p) are both greater than 5 (where np and n(1−p) are number of successes and number of failures)’. When comparing proportions across binary, categorical or ordinal data, the chi-squared distribution is often assumed; however, if the numbers in the categories in a 2 × 2 table become very small (<5 in any one category) then it is often more appropriate to use Fisher’s exact test, which is described in any standard statistical textbook.
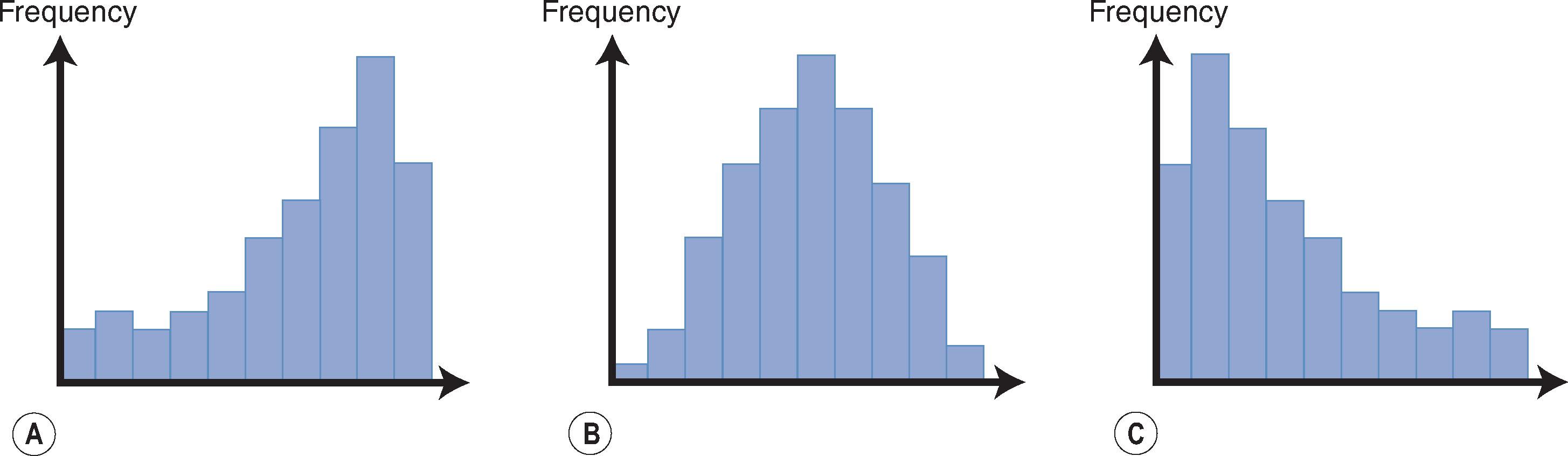
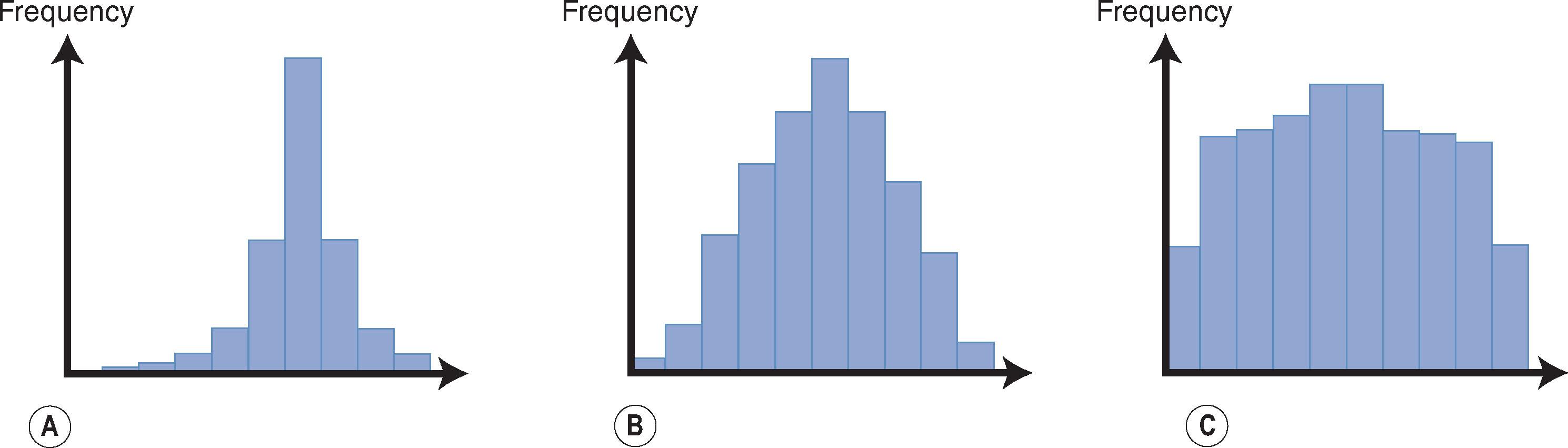
Probably the most common example of deciding whether to use a parametric or non-parametric test is when you want to know whether the continuous data in your sample can be assumed to follow a normal distribution. In general, for small samples of less than about 15 observations, it is not safe to assume the data are normally distributed, and non-parametric methods should generally be employed. However, it should be remembered that these tests are less powerful and the sample size is small, which will make the statistical results hard to interpret. If you have a reasonably large sample size, the first thing to do is to plot your data points on a scatter graph or group the data into bins and plot them on a histogram. Inspection of the graphs or histograms is the simplest way of assessing whether your distribution assumptions are valid. Deviations from the normal distribution can lead to significant skewness or kurtosis. Fig. 14.3 demonstrates histograms for data that follow a normal distribution or have a positively or negatively skewed distribution, and Fig. 14.4 shows how data can deviate from the classic ‘bell-shaped’ curve seen in the normal distribution and exhibit kurtosis. Kurtosis is concerned with the shape of the distribution and can have a considerable impact on the statistical analysis that you choose to perform on your data. When kurtosis is extreme, non-parametric tests should be used. It is worth noting that for data that are perfectly normally distributed, the mean, median and mode values are all the same, whereas for positively skewed data, the mean tends to be larger than the median and vice versa for negatively skewed data. When summarising skewed data (and also reporting descriptive results from a non-parametric test), it is often better to quote the median and interquartile range rather than the mean and SD, which are generally used for summarising normally distributed data. The way to calculate these summary statistics is described in the next section. In some cases, it helps to convert skewed data into another variable that can be assumed to follow the normal distribution (this is called transformation). For example, data that are positively skewed can often be manipulated into a more normally distributed format by transforming them onto the log scale; the t -test can then be used on the log-transformed data. There are more formal ways of testing your assumptions about the normal distribution, such as normal plots and Shapiro–Francia or Shapiro–Wilk tests, but these should be used cautiously and, if there is doubt, you should revert to using non-parametric methods.
There are numerous ways in which data can be summarised and presented, and the choice depends on the type of data. The previous section defined the different types of data and the distributions that are often assumed to analyse them. Table 14.2 shows some typical methods for summarising and presenting different data types. All statistical software packages will perform the analysis for summary statistics, but the following simple example shows how the basic ones can be calculated for a set of data.
| Data Type | Summary Statistics | Presentation |
|---|---|---|
| Quantitative or continuous | Mean or average, standard deviation, variance, standard error, confidence intervals, mode, median, range, interquartile range |
|
| Categorical, ordinal or binary |
|
|
| Time-dependent event outcomes |
|
|
For example, a study was conducted to investigate various aspects of pregnancy status, previous pregnancy, delivery type, birth weight and survival in a sample of 20 women recruited over 1 year and followed for 5 years.
This is the sum of all the observations divided by the number of observations.
For example, mean systolic blood pressure at 20 weeks’ gestation = (105 + 107 + 107 + … + 190 + 199)/20 = 144.35 mmHg.
Similarly, the mean age = 32.05 years.
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here