Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
The increasing complexity of biomedical research highlights the need for greater focus in the teaching of statistics and probability to physicians. Pharmaceutical and medical device literature can contain complicated statistical testing, making critical appraisal challenging. Academic studies that present potentially beneficial therapeutic advances are difficult to incorporate into practice when the experimental designs are not well understood. Further, patients often come armed with studies and claims from Internet resources and need help separating valuable information from dangerous conjecture.
In their most recent competencies, the Accreditation Council for Graduate Medical Education stated that physicians should be able to “locate, appraise, and assimilate evidence from scientific studies related to their patients’ health problems,” yet many physicians feel ill-equipped to do so. In a survey of British physicians, 79% of respondents considered probability and statistics important in their work, and 63% felt there was a part of their jobs that they could do better if they had a better understanding of probability and statistics ( ).
In the recent past, the statistics and experimental designs employed in medical research was not overly complicated. In fact, by today’s standards, many “classic papers” are significantly flawed in their design, have incorrect analysis applied, or make overly ambitious conclusions. As physicians and researchers continue to look for ways to advance patient care, increasingly rigorous studies are being published. Journal editors have addressed this by recruiting highly educated statistical consultants as reviewers and editors, and many journals now suggest that statisticians should be consulted prior to manuscript preparation.
Most physicians are not statisticians, nor do they have statistical experts readily available for daily consultations. So to be able to apply this body of increasingly complex research to patient care, physicians need to become educated consumers of research. Toward this end, this chapter will review the basic principles and concepts necessary for critical literature review. Attention will not be placed on performing specific statistical tests or on the mathematics behind them. Rather, a more intuitive approach will be used so that readers will understand the reasoning behind the common statistical tools and will be better able to appraise the literature.
Before delving into specific statistical tests or experimental designs, it is important to establish a few basic elements. The first of these are variable types and measures of “central tendency” (which are the ways to describe the number that reflects the middle of a data set). Typically, variables are classified as one of three scale types: numerical, ordinal, or nominal, which are described below.
Numerical scales reflect observations where the difference between the numbers has some concrete meaning. Blood pressure, height, and number of pregnancies are illustrative examples, and describing and testing this type of data is probably most familiar. Numerical scales can be further classified as continuous (weight) or discrete (number of pregnancies) data.
Means and standard deviations are typically used to describe both continuous and discrete numerical data. These are measures that most are familiar with and are the ones that are typically thought of when discussing central tendencies. The mean is calculated as the average value of the observations; the standard deviation (or its squared value, termed variance ) describes the spread around the mean. A common example is presented in Fig. 64.1 A.

Ordinal data is encountered frequently within the medical literature, making an intuitive knowledge of them crucial. These data can be placed in a logical order, but the differences between the individual points are not standardized. Mallampati score provides a succinct example, as it ranks the characterization of mouth opening to tongue size, but the difference in one’s confidence of a successful intubation from one level to the next may not be the same. Most practitioners believe that the difference between a Mallampati 1 to a Mallampati 2 does not reflect a large change in intubation difficulty, however many feel that moving from a 3 to a 4 should cause one to carefully consider alternative intubation techniques. Another common example is the popular 0 to 10 numerical pain score. In this case a pain of 8 is certainly worse than a 2, but a change in either to a 5 might not reflect the same change in pain intensity.
Percentages or proportions (further described below) are often used when describing ordinal data, but measures of “the average” of an ordinal data set are typically expressed by the median value. The median is the middle observation. Stated another way, the median is the value where half of the observations are higher and half are lower. Percentiles and interquartile ranges are used to describe the spread around the median value. A percentile is the percentage of the observations that are equal to or lower than some particular number. For example, 10 percent of the observations are less than the value that marks the 10th percentile. The interquartile range (illustrated in Fig. 64.1 B) describes the 25th and 75th percentile values. Between these two limits is the central 50% of the observations.
Finally, nominal scales categorize or describe the qualities of a data set and are often expressed as percentages or proportions. Examples of this include eye color or the type of anesthesia (general, sedation, or regional). Nominal data that can only be one of two values are termed dichotomous and are often analyzed with special statistics. Typical techniques for presenting nominal data include contingency tables or bar graphs ( Fig. 64.1 C). Variation ratios are sometimes used to describe the spread of nominal values, but they are not often used in the medical literature and will not be further described here.
With the variable types defined, we can now begin to discuss how to use data for medical decision-making and research. Most physicians are quite comfortable using clinical data for decision-making. Examples include using ST-segment elevation values to determine whether a myocardial infarction is taking place, measuring induration to a tuberculin skin test to determine whether someone is infected, or using point-of-care tests to detect pregnancy. But to fully understand the implications that a positive or negative test has on the likelihood that a person has the condition, the basics behind statistical decision analysis must be understood. These include a working understanding of sensitivity and specificity and the use of a receiver operating characteristic (ROC) curve, which characterizes the relationship between these two parameters.
The difference between sensitivity and specificity is easiest to understand using an example test that can return either a positive or negative result. For every population of people and any disease one can imagine, there are two groups: those with the disease and those without it. If we developed a screening tool to detect the presence of the disease, the results of the test could be characterized by the 2 × 2 shown in Table 64.1 . The sensitivity of the test is determined by the number of true positives divided by the total number of patients with the disease (a proportion). This number therefore represents the proportion of diseased patients detected by the test. When this number is high, the likelihood of missing a patient who has the disease would be low. Thus the test is sensitive to the presence of the disease. Stated another way, a false negative result is unlikely.
| PATIENT | |||
|---|---|---|---|
| Screening Test | Patient HAS the Disease | Patient DOES NOT Have the Disease | |
| Test is positive | True positive (TP) | False positive (FP) | PPV = TP/(TP + FP) |
| Test is negative | False negative (FN) | True negative (TN) | NPV = TN/(FN + TN) |
| Sensitivity = TP/(TP + FN) | Specificity = TN/(FP + TN) | ||
The specificity of a test is calculated by dividing the number of true negatives by the total number of patients without the disease. When this number is high, the test does not mislabel those without the disease. In this case a high value suggests that a negative test truly indicates that the patient does not have the disease: it is only positive in the presence of the specific disease. Correspondingly, a test with high specificity has a low false positive rate. Note that in Table 64.1 , the calculations for positive predictive value (the probability of a patient with a positive test to actually have the disease) and the negative predictive value (the percentage of patients with a negative test not to have the disease) have also been presented. These concepts are similar to sensitivity and specificity and should also be understood; the review by provides an excellent explanation of these and likelihood ratios, which is another important topic.
We will use data collected by in a study on intubation success as examples throughout much of this chapter. In that publication, it was stated that a composite measure of Mallampati class, cervical range of motion, normal mouth opening, presence or absence of teeth, and weight reflected the probability that the anesthesiologist would choose to use a videolaryngoscopic device instead of direct laryngoscopy for visualization during intubation. Assume that we can use that probability measure as a surrogate for intubation difficulty, and we choose a cutoff of 50% to represent a “positive” test result for a difficult intubation. The resulting data (presented in Table 64.2 ) shows that our sensitivity would be low, at 7.8%. The specificity, however, would be quite high, at 97.8%. Thus if we obtained a value of less than 50% for our prediction, we can feel comfortable that the patient will likely not be difficult to intubate.
| PATIENT | ||
|---|---|---|
| Screening Test | Difficult to Intubate | Not Difficult to Intubate |
| Prob > 50% | 14 | 34 |
| Prob < 50% | 174 | 1520 |
| Sensitivity = 14/(14 + 174) = 7.4% | Specificity = 1520/(34 + 1520) = 97.8% | |
But is this the test we would want? Most practitioners would rather overpredict the number of difficult-to-intubate patients and would therefore want a highly sensitive test. A perfect test would have a sensitivity and a specificity of 100%, but sensitivity and specificity are typically inversely related; increasing one decreases the other. To characterize this relationship, the ROC is used. As shown in Fig. 64.2 , this graph plots the value of sensitivity (true positive rate) on the y -axis against 1-specificity (equal to the false positive rate) on the x -axis as the cutoff score for a positive test is changed. The overall performance of the test improves as the apex of the graphed line approaches the left upper corner. The dotted line represents the line of zero discrimination, marking the area where our test is no better than a coin flip. Finally, the area under the ROC curve represents the probability that a randomly selected patient with a difficult intubation will have a higher test result than a randomly selected person that is not difficult.
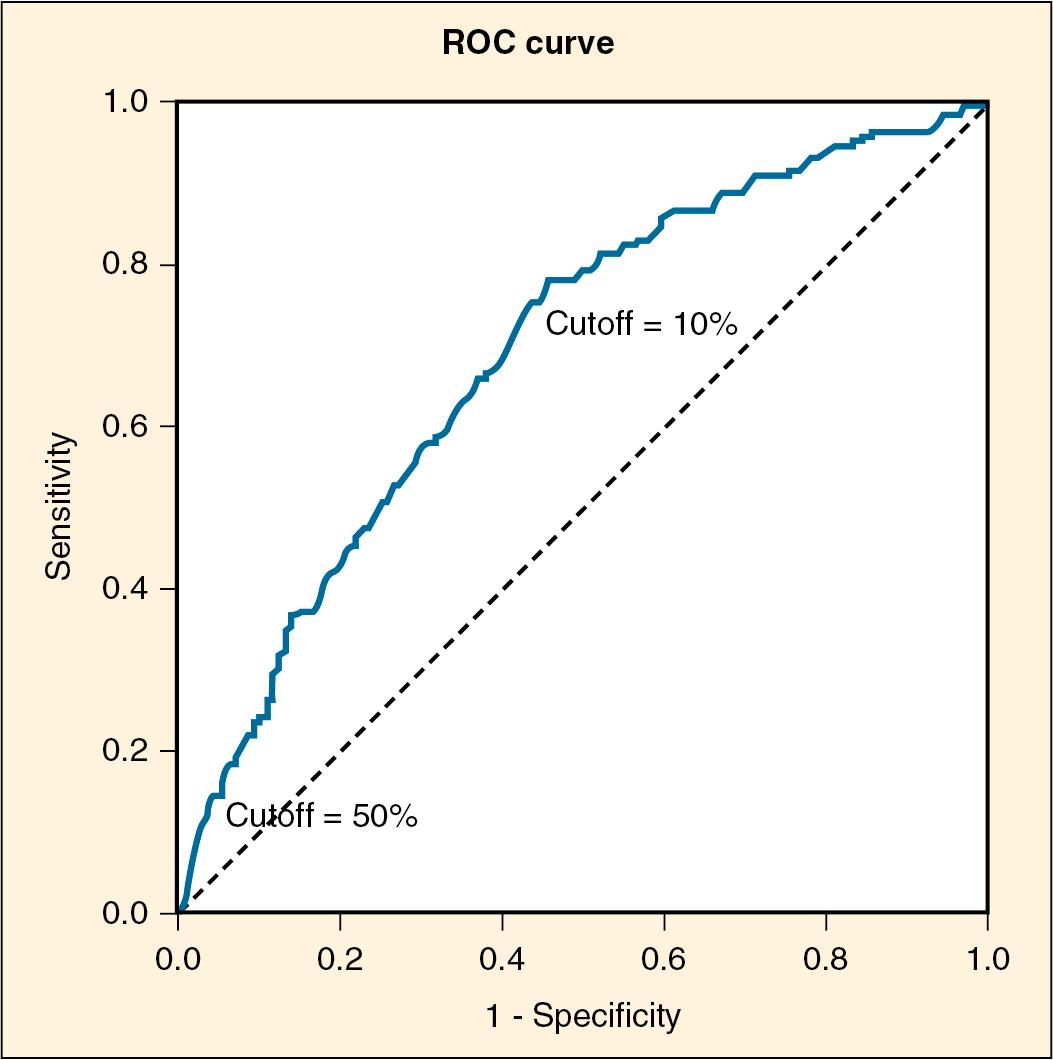
Continuing with the example, the 50% cutoff value provides a low sensitivity. From the ROC, we see that we can approach a sensitivity of 62% using a cutoff of 10% while maintaining a specificity of 65% (remember that ROC curves typically present 1-specificity), representing the point that would maximize both. Pushing the cutoff further would increase the sensitivity at the expense of being less specific (meaning more false positives). The area under the curve is 0.69, suggesting that the difficult-to-intubate patient will have a higher score than an easy patient almost 70% of the time. The balance between the sensitivity and specificity that are ideal for a particular test depends on the goal of the test. A screening test, for which the goal is to confidently rule out only those patients who do not have a disease, requires a sensitive test. If the goal is to rule a patient in, as with a confirmatory test, then high specificity is best.
Research studies involve more than just describing a sample of data. Groups are compared, associations are sought, and conclusions are drawn. To do this requires more than just looking at the numbers and declaring that a difference exists; instead, hypothesis testing is used to quantify the certainty in a declaration of difference. In this section, we will discuss the generation and testing of a hypothesis, using language meant to give the reader an intuitive sense of the process rather than statistical theory.
A hypothesis is a statement of prediction, in concrete and testable terms. The fact that it must be testable is important and differentiates it from an aim , which is a statement of overall purpose. For example, a statement such as “characterize the effects of etomidate” could be considered an aim, whereas “induction with etomidate result in smaller decreases in blood pressure than propofol” is a hypothesis. The latter is certainly testable and could help one toward the overall goal of the former. Conventional hypotheses state that a difference will be found, as opposed to an example hypothesis that “drug A and drug B will show similar decreases in pain score after administration.” Although this hypothesis would certainly be acceptable (and will be further discussed in the section on equivalence testing), it is more typical to test whether things are different rather than the same. This is done by assuming the “null hypothesis” is correct and then trying to prove that the null hypothesis is wrong with statistical testing. As an example, the null hypothesis from our etomidate example would be “the decreases in blood pressure seen after induction do not differ between etomidate and propofol.”
Two important concepts that should be briefly discussed before moving forward are populations and samples. When statisticians refer to populations, they are describing the entirety of a large set of elements believed to have something in common. An example, if we were trying to prove that diabetes shortens life expectancy, the population would be all of the diabetic patients in the world. Obtaining data from an entire population is impossible or completely impractical, however. Thus we use a subset of the population, termed the sample , as a surrogate for testing our hypothesis. We then try to generalize the results to the entire population using inferential statistics, like those discussed in the following sections. For medical research, populations typically refer to patients, however hospital systems, health care providers, or inanimate objects such as medical records could be the populations under investigation.
Sampling is typically accomplished in one of four ways. The first is simple (random) sampling, where each possible subject has the same chance of being assigned to the study. The most straightforward example is one where potential subjects are assigned a number, and numbers are selected (with random number generation software or even with a simple approach like drawing numbers out of a hat) to indicate who will be included in the sample. Although easy to understand, it requires that we identify each member of our entire study population. A more practical method would be systematic sampling, where every third patient in line at a general health clinic would be selected for our diabetes example above. Stratified sampling is similar, except that the population is first divided into smaller groups prior to randomizing. An example would be selecting a sample from a group of known insulin-dependent diabetics to compare against a control sample taken from age-matched nondiabetics. The above techniques are examples of probability sampling, as opposed to nonprobability sampling. In nonprobability sampling, the true probability that a particular subject might be chosen is unknown. Perhaps the most common example of nonprobability sampling is convenience sampling. In this technique, the sample is selected because it is convenient for the investigator (e.g., asking for volunteers from a medical school class). Generalization of convenience samples to the greater population is difficult because of sampling bias, but they are still common within medical research.
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here