Keratometry and Topography

Keratometry

Keratometry describes a method to measure the two principal meridional radii of curvature of the central cornea by measuring the size of mire reflections from the corneal surface. Each meridian of the central cornea is considered a section of a spherical convex reflecting mirror. From geometric optics, the magnification equation is:

where h′ is the height of the virtual image of the mire, h is the physical height of the mire, f is the focal length of the mirror, and x is the distance from the mire to the principal focus.

The focal length (f) of a convex mirror is given by:

where r is the radius of curvature. Then

or

Because the distance (x) from the mire to the focal point of the mirror surface is not known, the distance from the mire to the surface is used (d).

This dimension (d) is called the working distance and is a reasonable approximation if the distance from the mire to the surface is large compared with the focal length of the surface. Because the distance (d) from the keratometer to the surface (the cornea) can be fixed and the height of the mire (h) is known, one can solve for the radius of curvature (r) by measuring the size of the virtual image (h′). The keratometer is calibrated with measurements on test balls. Because the central area of the normal cornea is nearly spherical and the keratometer is designed to measure the curvature of the principal meridians at a 3–4-mm diameter, K readings can provide accurate measurements of curvature and cylinder within the pupil.

Although the radius of corneal curvature is useful for fitting contact lenses, corneal power is generally more useful for diagnostics and intraocular lens (IOL) calculations. Corneal power can be calculated from the radius of curvature:

where P is the corneal power, n′ is the corneal index of refraction, n is the index of refraction of air (1.000), and r is the corneal radius of curvature in meters. The index of refraction of the cornea is generally taken as 1.376. However, because the keratometer attempts to estimate the total refractive power of the cornea and not just the air-tear interface, a keratometric index of 1.3375, an effective index of refraction, is generally used instead. This accounts for the small negative power introduced by the posterior corneal surface. On average, the anterior cornea has a refractive power of approximately +48 diopters (D) of convergence and the posterior cornea −5 D of divergence. Thus Eq. (11.5 ) becomes:

The keratometric index makes several approximations, including the assumption of spherical radii of curvature for the anterior and posterior corneal surfaces. Corneal surgery or pathology that significantly alters corneal thickness or changes the curvature of the anterior and/or posterior cornea will introduce errors in this power relationship. Therefore K values used in IOL calculations should not be measured with keratometry in eyes that have undergone keratorefractive surgery or are irregular for any other reason; average central corneal power indices are available on several corneal topographers for this purpose.

In contrast to manual keratometry, autokeratometry allows for automated measurement of keratometric values. These devices also use reflective techniques, but the images of the reflected infrared mires are collected with infrared detectors and analyzed to calculate radii of curvature. The Tomey RC-5000 (Tomey Inc., Nagoya, Japan) and Topcon KR-8000 (Topcon Corp., Tokyo, Japan) autokeratometers measure corneal curvature at the flat and steep meridians in the central 3-mm zone and have been found to have excellent repeatability and reproducibility.

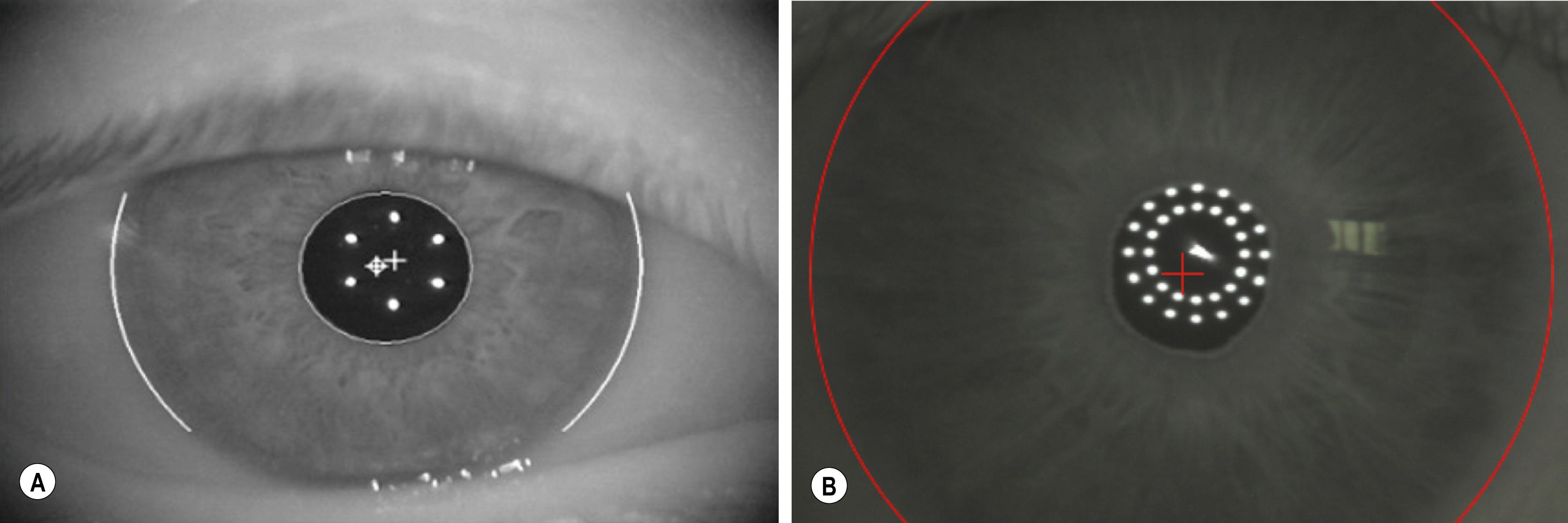
Optical biometers have been developed that can measure keratometric values in addition to other parameters necessary for IOL power calculation. The IOLMaster (Carl Zeiss Meditec, Jena, Germany), the first noncontact, optical biometer, uses partial coherence interferometry (PCI) to measure axial length (AL). The device calculates keratometry using six light-emitting diodes (LEDs) arranged in a circle, which are reflected off the anterior corneal surface to measure corneal curvature at a zone of approximately 2.3 mm ( Fig. 11.1 ). The Lenstar (Haag-Streit, Koeniz, Switzerland) uses optical lower-coherence reflectometry (OLCR) to measure AL and calculates keratometry in a similar manner but uses two circles with 16 points each, encompassing corneal zones with diameters of approximately 1.65 mm and 2.3 mm (see Fig. 11.1 ). ^, A large meta-analysis revealed no statistical difference in keratometry measurements between the two biometers. The IOLMaster 700 (Carl Zeiss Meditec, Jena, Germany) is a newer device that uses swept-source optical coherence tomography (SS-OCT) to generate optical cross-sections to calculate biometric parameters. The device calculates keratometry values in a similar fashion to the IOLMaster 500 and Lenstar using 18 reflected points that span zones out to an approximate diameter of 2.3 mm but also combines posterior corneal measurements obtained via SS-OCT with the anterior measurements to compute total keratometry (TK). Although experience with the TK power calculations is relatively new, the autokeratometry measurements have been found to have high repeatability and agreement with the earlier PCI and OLCR biometers. Other biometers have been recently introduced or are in development that use tomographic techniques to measure corneal power, in addition to their other measurements. The Galilei G6 (Ziemer Ophthalmic Systems AG, Port, Switzerland) and the Pentacam AXL (Oculus, Inc., Wetzlar, Germany) use Scheimpflug techniques to measure corneal curvature, whereas the Anterion (Heidelberg Engineering, Heidelberg, Germany) uses swept source OCT for corneal power calculation.

Corneal Topography

The result of efforts to extend measurement coverage of the corneal surface beyond the limited information provided by the keratometer, the modern corneal topographer emerged via a series of developments beginning with the keratoscope, followed by the photokeratoscope and then the videokeratoscope. The videokeratoscope, currently called the corneal topographer, combines video capture of corneal images with computer processing to provide maps of the corneal surface power distribution. All of these use a more complete target to examine a wider area of the cornea than the keratometer. The most commonly used target is still the Placido disk, which was introduced in 1880 and consists of concentric rings with alternating black and white mires.

Photokeratoscopes captured Placido reflections from the corneal surface to reveal irregular astigmatism in corneal grafts and surface distortion in moderate keratoconus. Unfortunately, they provided only qualitative information, and subtle, yet visually significant, distortions in corneal shape could not be detected by simple inspection of the mires. Doss published one of the first methods for calculating corneal power quantitatively from a photokeratoscope. Klyce extended this approach, exploring methods of representing the results for clinical application. Further advances included video capture of Placido disk images, automatic detection of mires, and calculation of corneal shape and power distribution, which led to the modern corneal topographer and the representation of corneal power with the color-coded contour map introduced by Maguire et al.

The rapid growth of keratorefractive surgery in the 1980s, along with the introduction of the personal computer, was the impetus driving corneal topography development. Corneal topography has been essential in diagnosing pathology, understanding visual complaints from early radial keratotomy (RK) and photorefractive keratectomy (PRK) cases, and evaluating new refractive surgery techniques. In screening for refractive surgery, corneal topography has become the standard of care. Since the introduction of Placido-based topography, other methods to measure corneal shape have been explored. These technologies include slit scanning tomography with Scheimpflug optics, raster stereography, scanning high-frequency ultrasound, holography, Fourier profilometry, optical coherence tomography, and grid-style reflection topography.

Devices for measuring corneal curvature and refractive power can be grouped in two categories: those that measure the anterior surface only and those that measure both the anterior and posterior corneal surfaces. Manual keratometry, automated keratometry, and reflection-based topography measure only the anterior corneal curvature and derive the total corneal power by reducing the corneal index of refraction from 1.376 to 1.3375 (in the United States) or 1.3320 (in Europe and other parts of the world) to account for the negative power of the posterior cornea. The underlying assumption is that the posterior curvature directly mirrors the anterior curvature, which may be a source of error. In contrast, slit scanning, Scheimpflug, and optical coherence tomography are able to directly measure both the anterior and posterior corneal surfaces to calculate the total corneal power using either Gaussian optics or ray tracing.

Placido Disk-based Topography

Placido disk-based topographers measure rings reflected from the anterior corneal surface ( Fig. 11.2 ). The first Purkinje image of the Placido target is digitized, and the radial position of points along the mires is determined in intervals as close as every one degree. Computer algorithms then calculate corneal curvatures consistent with the shapes of the mires. Close spacing of mires indicates relatively steep areas of the cornea, whereas broadly spaced mires overlie flatter regions. Although the algorithms used to calculate corneal curvatures vary considerably among different Placido-based topographers, with proper consideration, good accuracy can be achieved.

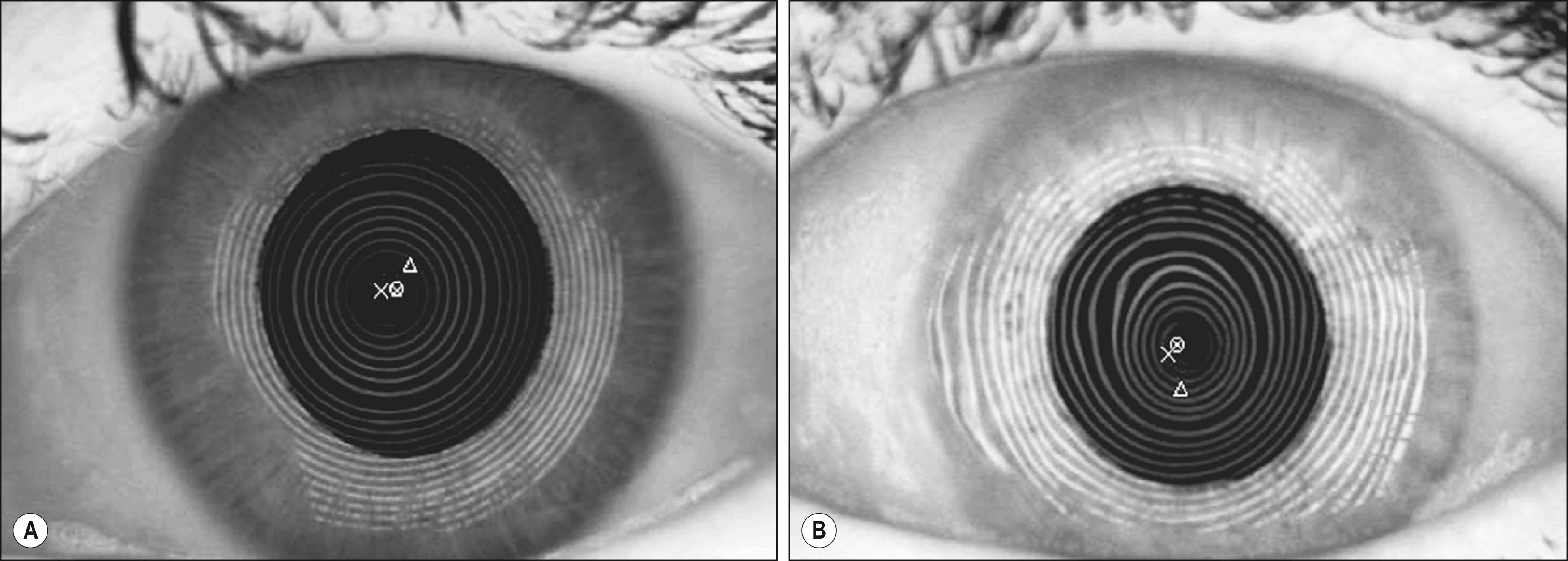
Although Placido topographers have good accuracy and repeatability and provide useful information on surface quality via their mires, they are not without limitations. Only the anterior surface is actually measured directly, and this technique is sensitive to disruptions in the tear film. Excessive delay of image capture following a blink can cause normal spherocylindrical corneas to exhibit irregularities due to tear film disruption. Thus topography should be performed prior to drop instillation and intraocular pressure measurement to maintain a regular, intact tear film.

Grid-Style Reflection Topography

Placido topography is reflection-based, which is an approach shared by a novel color-LED reflection topographer ( Fig. 11.3 ). The Cassini (i-Optics, The Hague, Netherlands) uses a grid-style target with point-to-point reconstruction of the specular reflections of color LEDs to determine corneal shape. This one-to-one correspondence between source points and image points helps to circumvent the skew ray problem encountered in Placido topography in which there is ambiguity in determining which point on the ring corresponds to which point on the image; this approach may thus allow for increased accuracy and precision.

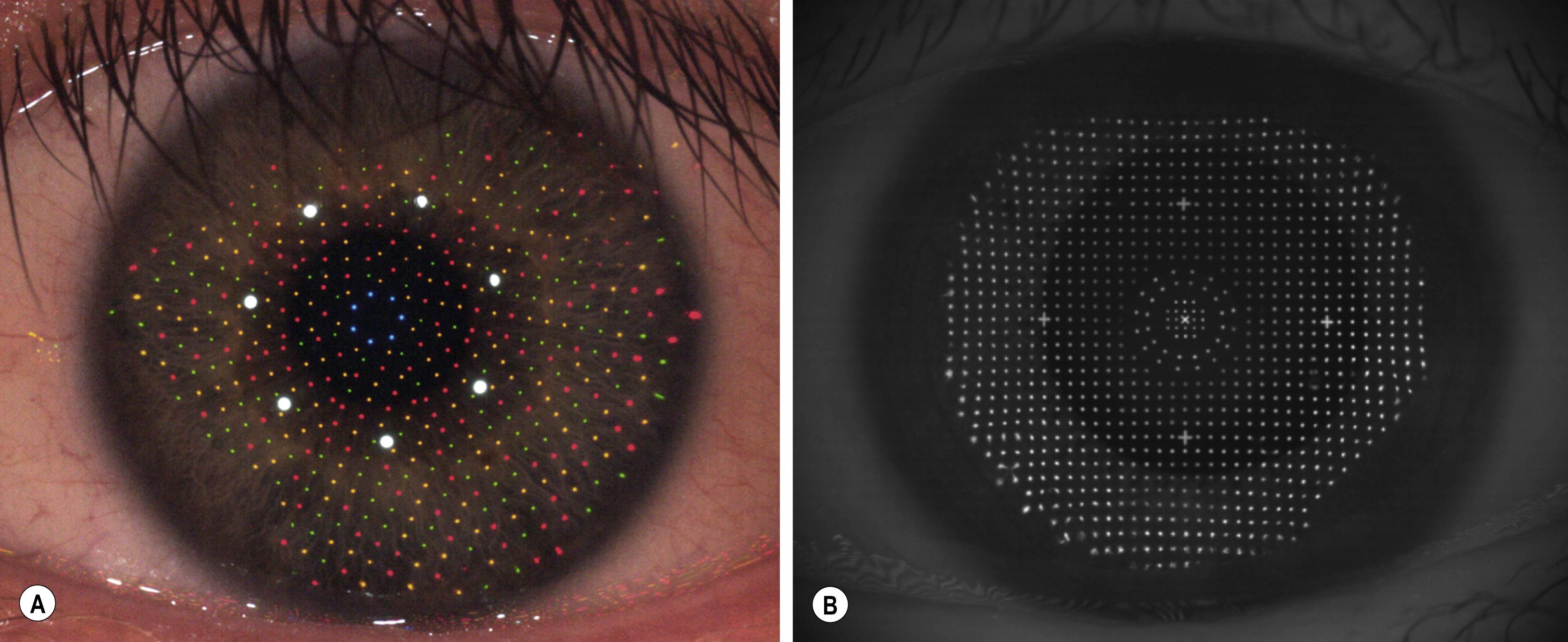
The iDesign (Abbott Medical Optics, Santa Ana, CA) aberrometer also calculates corneal topography using grid style reflection via the Hartman principle (see Fig 11.3 ). Uniformly illuminated spots arrayed in a Hartmann pattern are projected onto the cornea. Unlike Placido disk-based topography, actual data are captured from the central 3-mm zone without extrapolation. In addition, the lack of moving parts and high acquisition speed may lead to less motion artifact and centration errors. ^,

Slit Scanning Tomography

Slit scanning tomography uses a slit beam to capture light scatter from both anterior and posterior corneal surfaces, as during a slit lamp examination, to measure corneal shape and thickness. A series of slit beams are projected at regular intervals, and image analysis is used to determine locations of points on the corneal surfaces. The Orbscan (Model IIz, Bausch & Lomb, Rochester, NY), currently out of production, was the first commercially viable hybrid system that used Placido disk technology to display conventional corneal topography and scanning slits to determine corneal thickness ( Fig. 11.4 ). It projected slit beams at 45-degree angles 20 times on each side of the video axis in two 0.75-second intervals. Because the cornea is in constant motion from microsaccadic movements, ideal acquisition times are in the range of 30 ms. When actual measurement times exceed this, motion compensation is required to minimize the error in alignment of consecutive images.

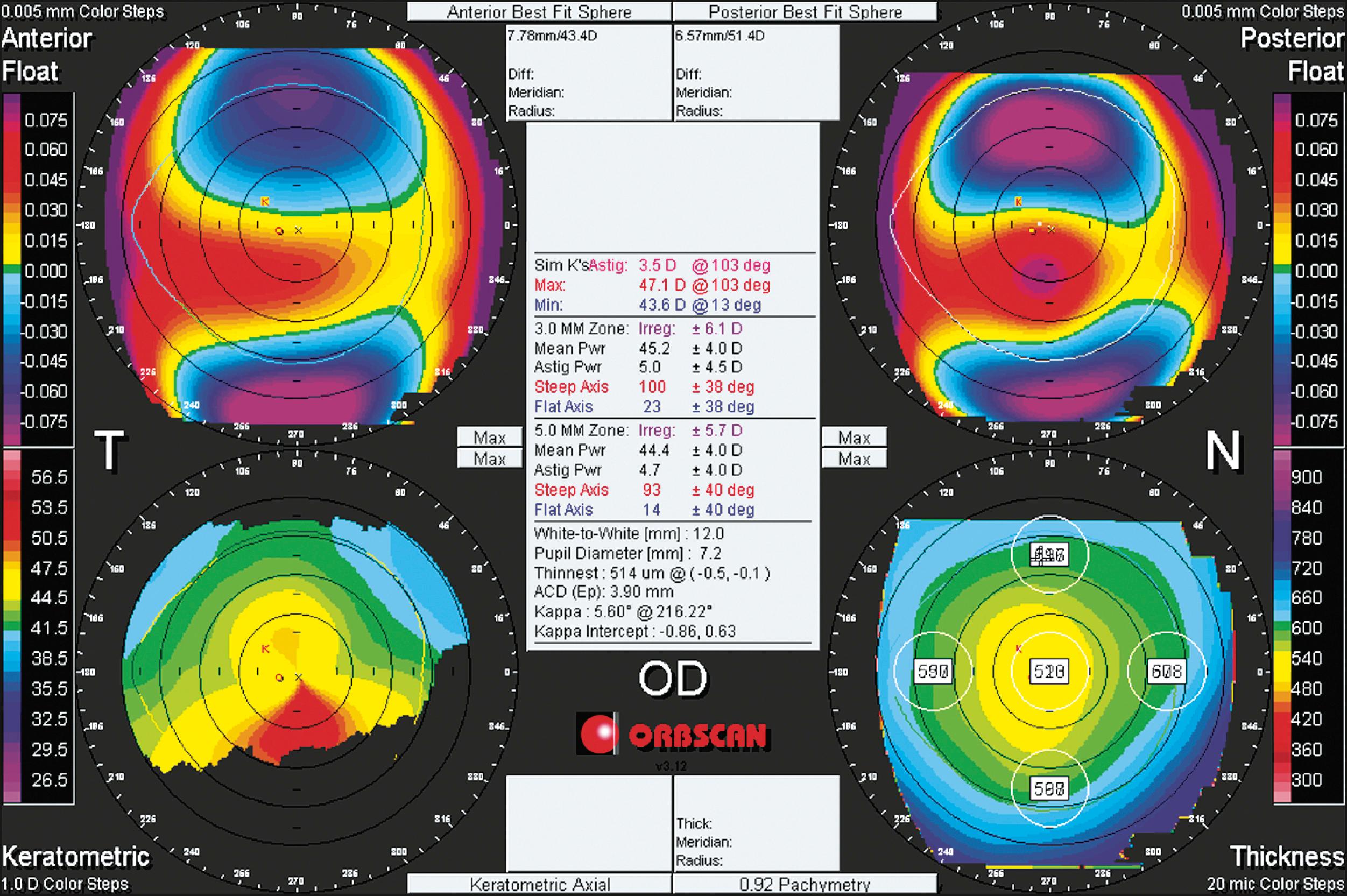
Because the elevation of each corneal surface is measured directly, errors in shape approximation are minimized, as in early Placido disk-based devices. For elevation-based devices to differentiate between two surfaces that differ in curvature by 0.25 D (the accepted target accuracy of Placido topography), they must be able to measure differences in surface elevation with a resolution of less than 1 micron. However, this is very difficult to achieve because elevation-based measurement is approximately 20 times less sensitive than Placido topography to changes in corneal power. An additional challenge in using slit-derived elevation data to calculate posterior corneal curvature and power is the difficulty in producing dual-surface calibration devices made of materials that mimic corneal light scattering. The accuracy of slit-based posterior elevation and pachymetric maps has not yet been resolved because of this.

Scheimpflug Tomography

In Scheimpflug tomography, sagittal sections of the anterior segment are photographed using Scheimpflug optics, which increases the depth of focus and enables simultaneous imaging of the cornea, anterior chamber, and lens. Unlike Placido disk-based devices, Scheimpflug tomographers can analyze the very center of the cornea and image both the anterior and posterior corneal surfaces. However, they cannot image the ciliary sulcus, and, like slit-scanning devices, require extremely high resolution to detect curvature differences.

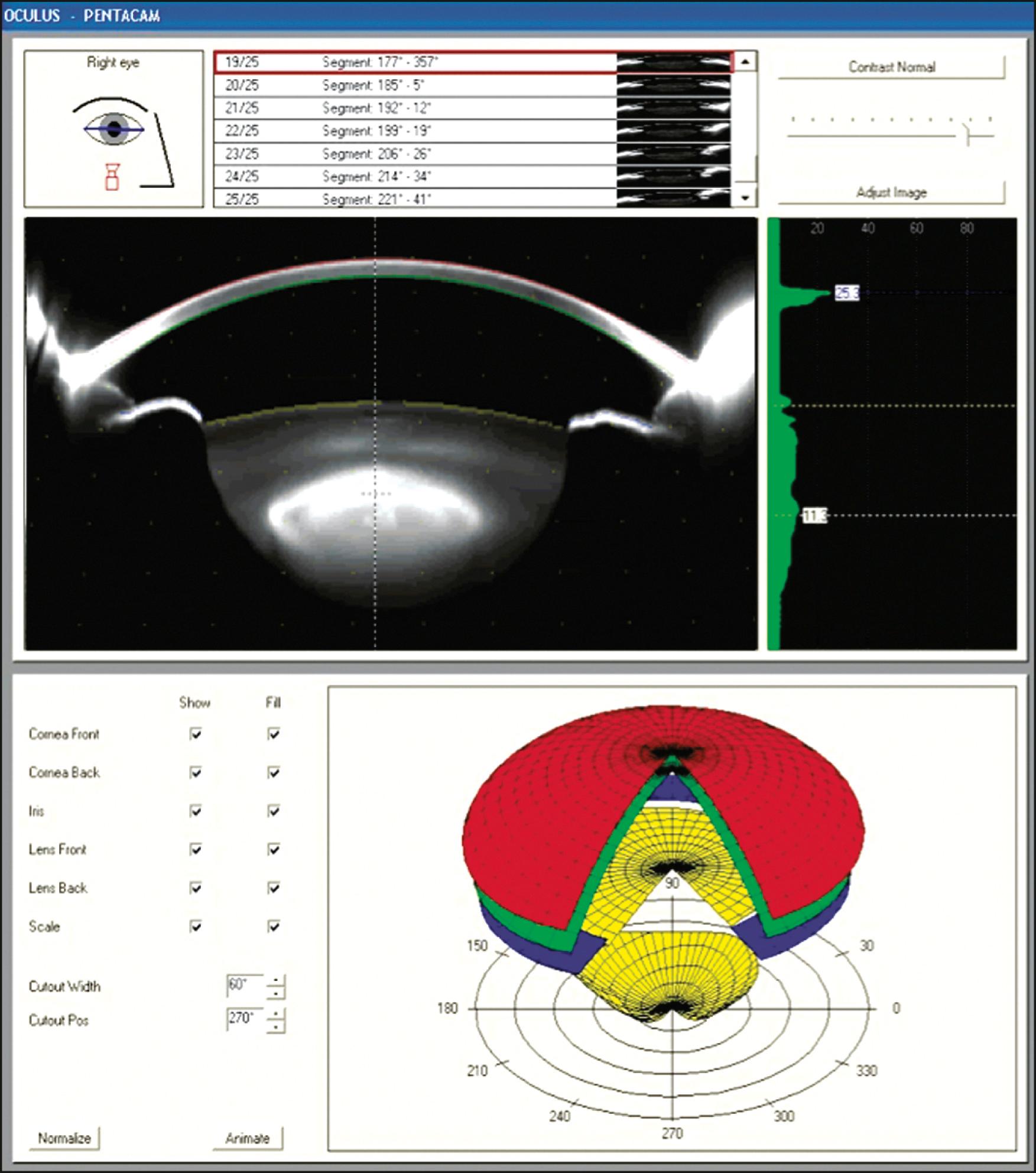
The Pentacam (Model HR, Oculus, Inc., Wetzlar, Germany) is a hybrid Placido-Scheimpflug device that rotates around the eye 180 degrees in 2 seconds, producing 50 images of both corneal surfaces and 138,000 elevation points to create a three-dimensional (3D) representation of the cornea ( Fig. 11.5 ). Like the Orbscan, the data must be translated and aligned to reduce errors due to eye movement during acquisition. The Sirius (Costruzione Strumenti Oftalmici, Florence, Italy) is another Placido-Scheimpflug hybrid device that records 25 Scheimpflug images and 1 keratoscopic measurement in less than 1 second. The Galilei (G4, Ziemer Ophthalmic Systems AG, Port, Switzerland) is a Placido-dual Scheimpflug analyzer that uses two Scheimpflug cameras rather than one. Elevation data are averaged from each camera, which occupies the gaps in the Placido rings. To fill in the gaps, two Placido images are recorded with cameras oriented both vertically and horizontally. By using two cameras, measurement errors due to angle of orientation and ocular decentration are greatly reduced.