Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
In the preceding chapters, we examined cardiovascular regulation at several different levels. Powerful systemic mechanisms operate over both the short term and the long term to control mean arterial pressure and cardiac output. Operating independently of these are local mechanisms of control that regulate blood flow at the microcirculatory level. In addition, individual organs have their own unique tools for managing specific circulatory requirements. In this chapter, we put it all together and learn how the cardiovascular system integrates the complex systemic, local, and individualized regulatory mechanisms in response to the demands of everyday life.
In the previous chapters, we often presented physiological responses in a linear sequence or on a linear chart. For instance, we might represent the carotid-baroreceptor feedback loop (see p. 534 ) as a linear sequence of events ( Fig. 25-1 A ). However, cardiovascular parameters and associated physiological responses are often related by multiple factors, requiring a more complex diagram called a branching tree (or an algorithmic tree). For example, in our discussion of the control of cardiac output (see pp. 545–548 ), we started with the knowledge that cardiac output depends on two parameters—stroke volume and heart rate. Therefore, with our very first step, we come to a fork in the road—an example of a branching tree (see Fig. 25-1 B ). At the next level, we encounter a pair of forks because stroke volume and heart rate both depend on two parameters. Finally, at the third level, we see that each of the determinants of stroke volume and heart rate depends on multiple factors (i.e., multiple forks).
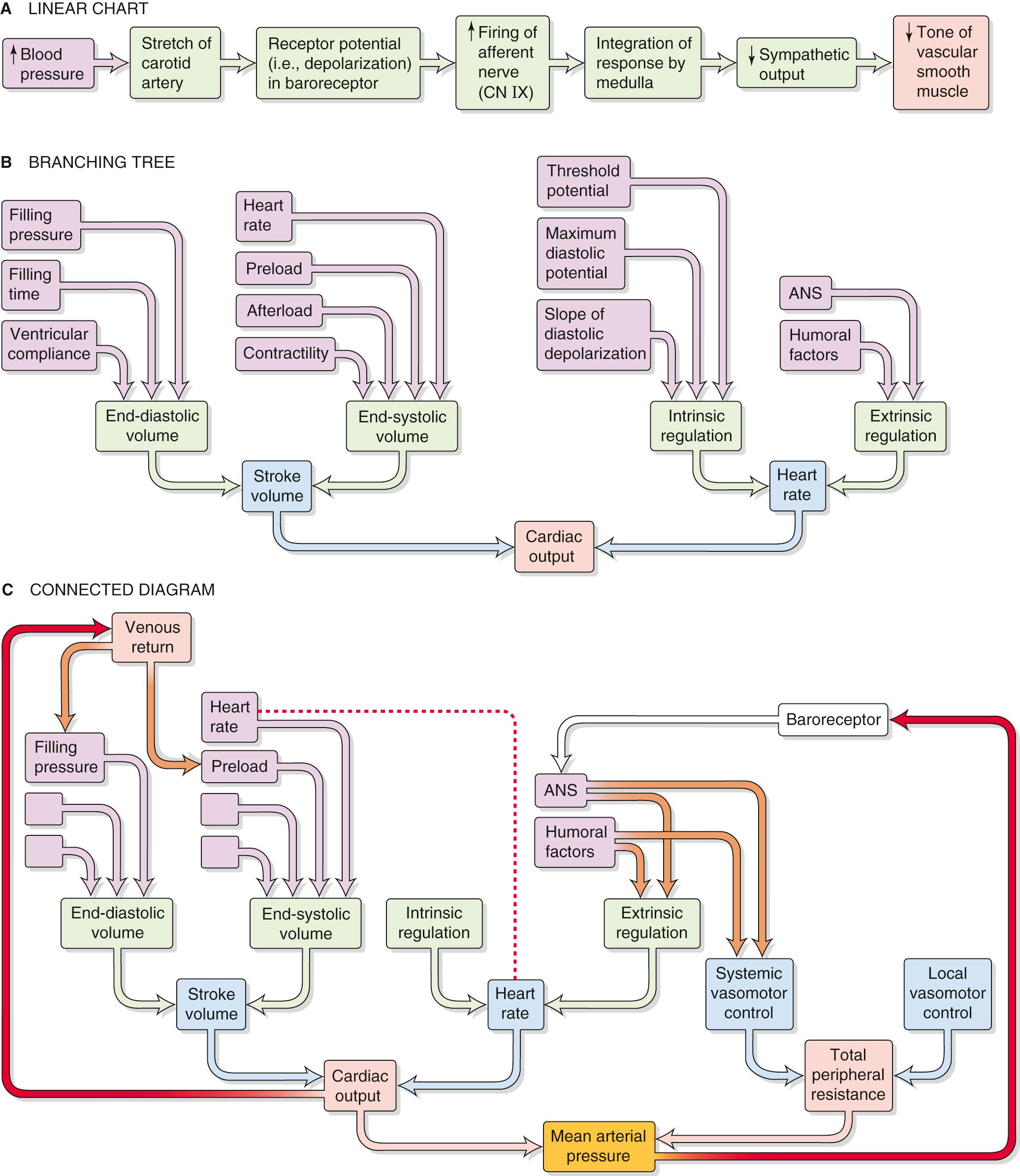
The control of some cardiovascular parameters is even more complex, requiring that we graft branches from smaller trees. For example, we know from Ohm's law that mean arterial pressure depends on both cardiac output (and all the elements in its branching tree in Fig. 25-1 B ) and total peripheral resistance, which requires a branching tree of its own (see Fig. 25-1 C ). Moreover, sometimes an element in one part of the “forest” interacts with another element that is far away. A physiological system with such complex interactions is best represented by a connected diagram, which may include feedback loops (see Fig. 25-1 C , red arrows), parameters that appear more than once in the tree (connected by a red dashed line), or factors that modulate parameters in two different branches of the tree (connected by brown arrows). Although not shown in Figure 25-1 C , several feedback loops may impinge on a single element, and some loops are more dominant than others. The complex interactions among parameters make it difficult to distinguish factors of overriding importance from those of lesser weight. Moreover, when one disturbs a single parameter in a complex physiological system, the initial state of other parameters determines the end state of the system. In previous chapters, we have chosen situations that artificially isolate one portion of the cardiovascular system (e.g., heart, microcirculation) to explain in a simple way the homeostatic control mechanisms that govern that subsystem. However, conditions isolating subsystems rarely apply to a real person.
How can we evaluate which parameters are crucial? As an example, consider one subsystem, the heart. Let us assume that we can rigorously analyze all determinants of cardiac function—such as Starling's law, force-velocity relationships, effect of heart rate on contractility, and so forth. These analyses take the form of mathematical expressions, which we can combine by systems analysis to create a model that describes the behavior of the entire heart—at least theoretically. How can we test whether our model is reasonable? We can compare the physiological response of the heart in vivo with the response predicted by a computer simulation of the model. Using this approach, we may be able to establish whether we have used the correct feedback loops, whether we have assigned proper values to various elements, and whether we have assigned the proper weight to each interaction. In this way, we can use any agreement between the experimental data and the performance of the model as evidence—but not proof—that the concepts contained in the model are reasonable.
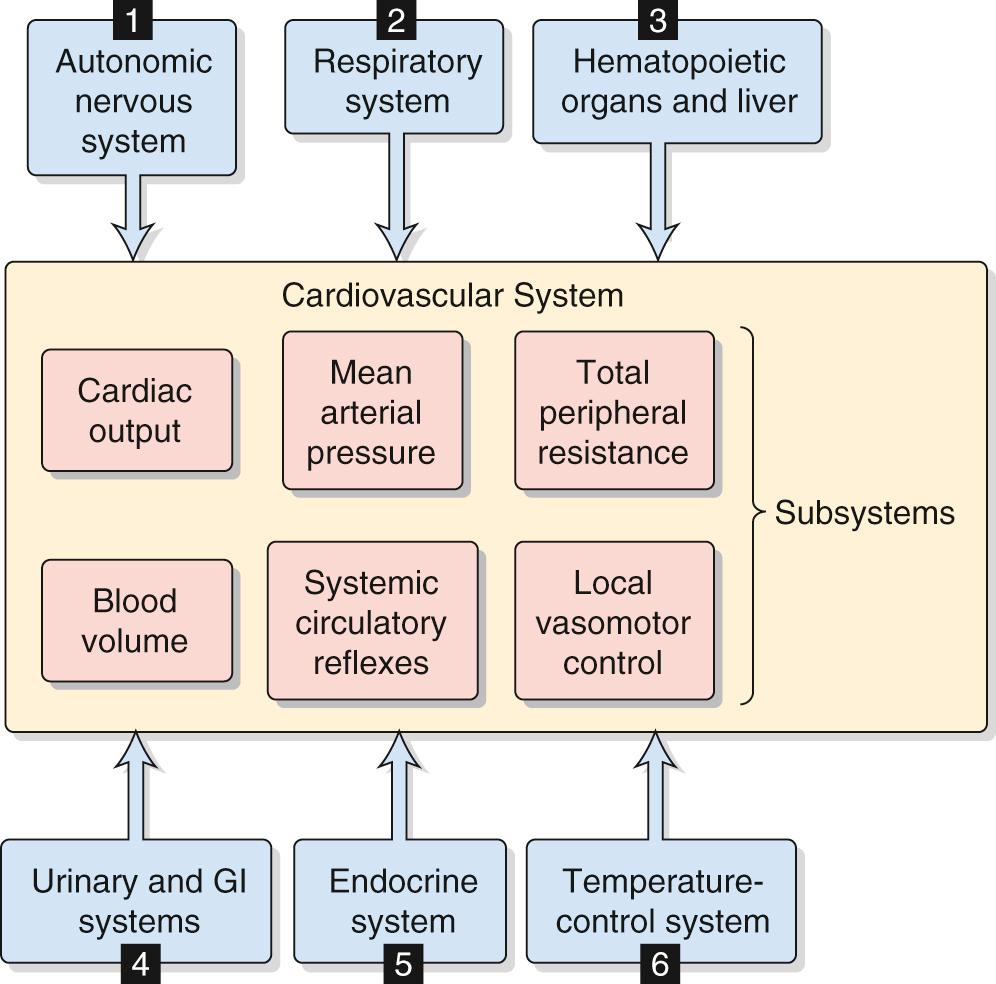
In performing a systems analysis of the entire cardiovascular system, we must consider the interrelationships among the various subsystems summarized in the central yellow block of Figure 25-2 . Not surprisingly, we cannot fully understand how a particular disturbance affects the overall circulation unless we consider all subsystems in an integrated fashion. For instance, consider the effects of administering norepinephrine, which has a high affinity for α 1 adrenoceptors, less for β 1 adrenoceptors, and far less for β 2 adrenoceptors. These receptors are present, in varying degrees, in both the blood vessels and the heart. A branching tree would predict the following. Because α 1 adrenoceptors (high affinity) are present in most vascular beds, we expect widespread vasoconstriction. Because β 2 adrenoceptors (low affinity) are present in only a few vascular beds, we predict little vasodilation. Because β 1 adrenoceptors (intermediate affinity) are present in pacemaker and myocardial cells of the heart, we would anticipate an increase in both heart rate and contractility and therefore an increase in cardiac output.
Although our analysis predicts that the heart rate should increase, in most cases the dominant effect of intravenous norepinephrine injection is to slow down the heart. The explanation, which relies on a connected diagram, is that increased peripheral resistance (caused by stimulation of α 1 receptors) and increased cardiac output (caused by stimulation of β 1 receptors) combine to cause a substantial rise in mean arterial pressure. The baroreceptor reflex (see red arrow on right in Fig. 25-1 C ) then intervenes to instruct the heart to slow down (see p. 534 ). However, bradycardia may not occur if many vascular beds were dilated before the administration of norepinephrine; in this case, the rise in blood pressure would be modest. Bradycardia might also not occur if the baroreceptor reflex were less sensitive, as would be the case in a chronically hypertensive patient (see Box 23-1 ). Thus, the effect of intravenous administration of norepinephrine on heart rate depends on the pre-existing state of various subsystems.
In trying to understand the integrated response of the cardiovascular system to an insult, we must include in our analysis not only all the subsystems of the cardiovascular system but also the pertinent control systems outside the circulation (see blue boxes in Fig. 25-2 ):
Autonomic nervous system (ANS). Part of the ANS is intimately involved in cardiovascular control (e.g., high-pressure baroreceptor response). On the other hand, a generalized activation of the ANS, such as occurs with the fight-or-flight response (see p. 347 ) also affects the circulation.
Respiratory system. We have already seen that ventilatory activity converts the intrinsic bradycardia response to tachycardia during stimulation of the peripheral chemoreceptors (see p. 545 ). In addition, the action of the respiratory muscles during inspiration causes intrathoracic pressure to become more negative (see p. 607 ), thereby increasing venous return. A third example is that the evaporative loss of water during breathing reduces total body water and, ultimately, blood volume.
Hematopoietic organs and liver. These systems control blood composition in terms of cell constituents and plasma proteins. The hematocrit and large proteins (e.g., fibrinogen) are major determinants of blood viscosity (see pp. 437–439 ) and therefore of blood flow. Because the plasma proteins also determine colloid osmotic pressure (see p. 470 ), they are a major component of the Starling forces (see pp. 467–468 ), which determine the distribution of extracellular fluid (ECF) between the interstitium and the blood plasma.
Gastrointestinal and urinary systems. Because the gastrointestinal tract and kidneys are the principal organs determining input and output of electrolytes and water, they are mainly responsible for controlling the volume and electrolyte composition of ECF. ECF volume plays a central role in the long-term control of blood pressure (see p. 838 ).
Endocrine system. Part of the endocrine system is intimately involved in cardiovascular control (e.g., epinephrine release by the adrenal medulla). Other hormones influence the cardiovascular system either because they are vasoactive agents (see pp. 551–554 ) or because they regulate fluid volume and electrolyte composition by acting on the kidney and gastrointestinal system.
Temperature control system. The cardiovascular system is a major effector organ for thermoregulation, carrying blood from the body core to the skin, where heat loss then occurs (see pp. 1200–1201 ). In part, this heat loss occurs as sweat glands secrete fluid that then evaporates. However, the loss of ECF volume reduces the effective circulating volume (see pp. 554–555 ).
Inclusion of control elements outside the circulation (see Fig. 25-2 ) in our connected diagram of the cardiovascular system (see Fig. 25-1 C ) would expand the computer model to include hundreds of independent and dependent variables. Rather than trying to grasp such an exhaustive model, we work here through the integrated cardiovascular responses to four important circulatory “stresses”: (1) orthostasis (i.e., standing up), (2) emotional stress, (3) exercise, and (4) hemorrhage.
About two thirds of the total blood volume resides in the systemic veins (see pp. 448–450 ). When a recumbent subject assumes an upright position, the blood shifts from the central blood volume reservoirs and other veins to large veins in the dependent limbs. In discussing Figure 17-8 B , we assumed that the cardiovascular system somehow made the adjustments necessary to keep right atrial pressure (RAP) constant at about +2 mm Hg. Indeed, unless compensatory mechanisms intervene, blood redistribution will lower not only arterial blood pressure but also venous return and thus cardiac output.
To illustrate the effect of blood redistribution on venous return, we will represent the entire circulatory system by a horizontal, distensible cylinder 180 cm in length (the height of our person) and 3 cm in radius ( Fig. 25-3 A ). This cylinder holds ~5000 mL of blood (the normal blood volume). We know that immediately after a cardiac arrest, the entire vascular system will have a mean systemic filling pressure (MSFP) of ~7 mm Hg (see p. 549 ). The MSFP is the pressure in the circulation that would remain in the absence of any pumping or any gravity effects. Thus, if a subject is recumbent and has no heartbeat, and if the cardiovascular system is filled with a normal blood volume of 5000 mL ( V o ), the overall compliance of the system will produce a uniform pressure of ~7 mm Hg. If we were to transfuse an additional 100 mL (Δ V ) of blood into our cylinder, the MSFP would rise by ~1 mm Hg (Δ P ). We can conclude that the compliance, expressed as a normalized distensibility (see p. 454 ), is
Thus, for every 2% increase in blood volume, the MSFP of the cylinder increases by 1 mm Hg.

What will happen to our cylinder if we now turn it upright? This position is called orthostasis (from the Greek orthos [upright] + histanai [to stand]). Because we have a vertical column of blood 180 cm tall, we must now consider gravity (see Fig. 25-3 B ). The highest pressures will be at the bottom of the cylinder. ( Fig. 17-8 shows that orthostasis causes venous pressure at the ankle to rise from 5 to 100 mm Hg.) Therefore, our cylinder will distend maximally at the bottom, and this distention represents a shift in blood volume. The bottom of the cylinder (corresponding to the “dependent areas” of a person) gains volume, whereas the top (i.e., corresponding to the cranial portion of a person) loses blood volume. In fact, there would be no blood at all at the top of the cylinder.
By just how much would the column of blood fall in our upright, 180-cm-tall cylinder? If the overall vascular volume distensibility were 0.02/(mm Hg), then the actual height of the blood column inside the cylinder would be only about 100 cm. ![]() N25-1 If the heart were 50 cm below the top of the cylinder, then the top of the column would now be ~30 cm below the level of the heart. Therefore, there would be no blood to return to the heart. Moreover, the RAP would be negative (−30 cm H 2 O, or about −22 mm Hg). Because the heart cannot create a vacuum this large at its input by “sucking” blood—in fact, the heart must be filled by a positive RAP—cardiac output would fall to zero.
N25-1 If the heart were 50 cm below the top of the cylinder, then the top of the column would now be ~30 cm below the level of the heart. Therefore, there would be no blood to return to the heart. Moreover, the RAP would be negative (−30 cm H 2 O, or about −22 mm Hg). Because the heart cannot create a vacuum this large at its input by “sucking” blood—in fact, the heart must be filled by a positive RAP—cardiac output would fall to zero.
Equation 19-4 and the identical Equation 25-1 both describe how the “relative” or “normalized” distensibility depends on the relative change in volume (Δ V / V o ) and the pressure difference (Δ P ):
We can now solve for the relative change in volume:
For a very thin disk of fluid (height h ) in the upright vessel, the change in volume (Δ V ) is due solely to a change in vessel radius. In other words, because V = h π r 2 , Δ V = h π(Δ r ) 2 . Thus, we can rewrite Equation NE 25-2 as
In order to compute the shape of the upright vessel in Figure 25-3 , the only other thing we need to know is how Δ P varies with height in the upright vessel. For a hydrostatic column, the pressure increases linearly as we descend to greater depths, as described by Equation 17-4 . We reproduce this equation here:
Here, ρ is the density of the liquid, g is the gravitational constant, and h is the height of the column. We could use this equation to compute the pressure in dynes per square centimeter or pascals. However, physiologists tend to express pressures in centimeters of H 2 O or millimeters of mercury. For example, in Figure 25-3 B , the pressure at the bottom of the 100-cm column is equivalent to 100 cm H 2 O, which is also (knowing the density of mercury) 73.5 mm Hg.
Now we can compute the relative distention at the bottom of the upright cylinder, which is under a pressure of 73.5 mm Hg. Rearranging Equation NE 25-3 and solving for Δ r (the change in radius), we have
Because the initial radius ( r o ) of the horizontal cylinder in Figure 25-3 A was everywhere 3 cm, the distended radius at the bottom of the upright column has increased by 3.6 cm for a total radius of 6.6 cm—in other words, the radius has more than doubled, and the volume has more than quadrupled (i.e., increased by a factor of 4.8).
If the relative distensibility were less (e.g., 0.01/mm Hg in Fig. 25-3 C ), then the Δ r would also be less at the bottom of the upright cylinder. On the other hand, because the Δ r is less at each height, the column of water would have to be higher to accommodate the volume. Thus, the pressure at the bottom of the column would be greater (i.e., 130 cm H 2 O or 95.6 mm Hg in the example of Fig. 25-3 C ). As in Equation NE 25-5 , we can compute the relative distention at the bottom of the upright cylinder, which this time is under a pressure of 95.6 mm Hg:
In other words, uniformly reducing the relative distensibility by a factor of 2 still results in a near doubling of the radius and a near quadrupling of the volume (i.e., increased by a factor of 3.8).
If our model predicts that orthostasis should cause RAP to fall to −22 mm Hg, how is it that the body manages to maintain RAP at about +2 mm Hg in the upright position? The answer is that pooling of blood in the dependent vessels is much less pronounced during orthostasis than would be predicted by Figure 25-3 B , where ~2.3 L disappeared from the top of the cylinder. The actual amount of pooling in both legs of a real person is only ~500 mL. ![]() N25-2 Four major factors help reduce pooling and maintain RAP.
N25-2 Four major factors help reduce pooling and maintain RAP.
In the example shown in Figure 25-3 B , the column of blood would reach a height of 100 cm. Because the horizontal cylinder in Figure 25-3 A had a length of 180 cm, turning the vessel upright reduced the length of the column by 80 cm. How much volume moved into the lower part of the distensible, upright vessel? The answer is the volume at the top of the white region in Figure 25-3 B , which is the product of the 80-cm length and cross-sectional area:
In our cylinder example, the blood was initially distributed evenly throughout the length of the cylinder. In a recumbent human, however, most of the blood in large veins is located in the central blood volume (see p. 449 ), that is, the vessels near the heart. If a large fraction of the blood had started off in the head, the orthostatic shift of blood would have been more dramatic, as in Figure 25-3 B . The majority of the 500 mL of blood that pools in the legs during orthostasis comes from the intrathoracic vascular compartments. What is the sequence of events by which blood volume redistributes during orthostasis? As one stands, the output from the heart for a number of beats exceeds the venous return into the thoracic pool. This excess blood ends up filling the vessels in the dependent regions of the body. The result is a net transfer of blood—by way of the heart—from the intrathoracic vascular compartments to the dependent vessels.
In Figure 25-3 B , we assumed a relative distensibility of 0.02/(mm Hg). If we had instead used a value of 0.01/(mm Hg)—that is, if the vessels were less distensible—standing would cause a less dramatic shift of blood to the dependent vessels, ~1.4 L (see Fig. 25-3 C ) instead of ~2.3 L (see Fig. 25-3 B ). ![]() N25-1 As a result, the height of the blood column would fall from 180 to only 130 cm (see Fig. 25-3 C ) in the upright position, rather than to 100 cm (see Fig. 25-3 B ). Assuming a lower distensibility for the leg veins is reasonable because small vessels are far stiffer than larger ones, such as the aorta and vena cava. With the lower relative distensibility of 0.01/(mm Hg), the column of blood would just reach the heart. Indeed, when a subject stands quietly, the zero effective pressure level—the height in the body where vascular pressure equals atmospheric pressure—is about at the level of the right atrium. Obviously, if the circulatory system reduces its distensibility even further through the regulated contraction of vascular smooth muscle (discussed below), the height of the column of blood will increase and improve venous return.
N25-1 As a result, the height of the blood column would fall from 180 to only 130 cm (see Fig. 25-3 C ) in the upright position, rather than to 100 cm (see Fig. 25-3 B ). Assuming a lower distensibility for the leg veins is reasonable because small vessels are far stiffer than larger ones, such as the aorta and vena cava. With the lower relative distensibility of 0.01/(mm Hg), the column of blood would just reach the heart. Indeed, when a subject stands quietly, the zero effective pressure level—the height in the body where vascular pressure equals atmospheric pressure—is about at the level of the right atrium. Obviously, if the circulatory system reduces its distensibility even further through the regulated contraction of vascular smooth muscle (discussed below), the height of the column of blood will increase and improve venous return.
An important compensation for blood pooling during orthostasis comes from skeletal muscle contraction. When a person stands, the muscles of the legs and abdomen tighten. The presence of valves in the veins, as well as intermittent muscular movement, contributes to the flow of blood upward along the veins (see Fig. 22-7 C and Fig. 24-6 ). Vessels of the abdominal region remain nearly unaffected by orthostasis because the abdominal viscera are contained in a water-filled jacket that is maintained by the tone of the abdominal muscles.
Because of decreased venous return, cardiac output tends to fall by ~20% soon after one assumes an erect position. However, the fall in cardiac output would be even greater in the absence of autonomic reflexes. The decreased venous return leads to a fall in RAP, which in turn leads to a decrease in stroke volume and thus arterial pressure. High-pressure baroreceptors (see pp. 534–535 ) sense this decrease in arterial pressure, ![]() N25-3 which leads to an increased sympathetic output that raises vascular tone throughout the body and increases heart rate and contractility. Together, the constriction of arterioles (which raises total peripheral resistance) and the increased heart rate restore the systemic mean arterial pressure, despite a small decrease in stroke volume. In the dependent regions of the body, the sympathetic response also increases the tone of the veins, thereby decreasing their diameter and their capacity (compare Fig. 25-3 B and C ).
N25-3 which leads to an increased sympathetic output that raises vascular tone throughout the body and increases heart rate and contractility. Together, the constriction of arterioles (which raises total peripheral resistance) and the increased heart rate restore the systemic mean arterial pressure, despite a small decrease in stroke volume. In the dependent regions of the body, the sympathetic response also increases the tone of the veins, thereby decreasing their diameter and their capacity (compare Fig. 25-3 B and C ).
As noted in the text (see p. 576 ), orthostasis leads to the following sequence of events: Decreased venous return → fall in RAP → decrease in stroke volume → decreased arterial pressure → response of high-pressure baroreceptors (see pp. 536–537 ) → increased sympathetic output → generalized vasoconstriction and increased heart rate/contractility. Because RAP falls early in this sequence, you might wonder what role the atrial low-pressure baroreceptors play in the response. Reduced atrial stretch has little effect on heart rate (see pp. 547–547 ) and causes an increase in sympathetic output only to the kidney (i.e., causing renal vasoconstriction). Therefore, the low-pressure baroreceptors make only a minor contribution to the overall orthostatic response (i.e., generalized vasoconstriction and increased heart rate/contractility).
In summary, of the four factors that contribute to the stability of RAP during orthostasis, two are anatomical (i.e., nonuniformities of initial blood volume distribution and distensibility) and two are physiological (i.e., muscle pumps and autonomic reflexes). The two physiological mechanisms are both important. Indeed, after a lumbar sympathectomy, patients tend to faint when standing. However, after some months, they are able to compensate, perhaps by using the muscle pumps more effectively or by enhancing the sympathetic response of the heart.
The extent of the orthostatic response —how much the heart rate or peripheral vascular resistance increases under the control of the ANS—depends on a variety of factors ( Table 25-1 ), which involve nearly the entire cardiovascular system. Because these factors may differ from person to person or may differ within any one individual according to the circumstances, the orthostatic response is highly variable. We now discuss two examples of this variability.
| Total blood volume |
| Distribution of blood volume |
| Size of vessels in dependent regions of the body |
| Vascular distensibility |
| Mean systemic filling pressure (pressure in the absence of cardiac output) |
| Level at which zero effective pressure is normally located in a particular individual |
| Degree of tilt |
| Skeletal muscle tone; strength and rate of intermittent contraction of skeletal muscles |
| Vascular sufficiency |
| Abdominal muscle tone |
| Temperature |
| Response of low-pressure receptors |
| Response of high-pressure baroreceptors |
| Activity of the sympathetic system |
| Initial heart rate |
| Initial myocardial contractility |
| Sensitivity of vascular smooth muscle to sympathetic stimulation |
* That is, by how much standing up increases heart rate and peripheral vascular resistance.
In very sensitive subjects lying on a tilt table, a sudden orthostatic tilt can cause such a large fall in arterial pressure that the individual becomes dizzy or even faints. Fainting is caused by a transient fall in arterial pressure that causes cerebral perfusion to become inadequate.
In a cool environment, in which the arterioles in the lower extremities are constricted, the initial dip in arterial pressure can be small, despite the decrease in stroke volume. The explanation is that the high arteriolar resistance delays the transfer of blood from the thoracic pool to the legs. As a result, the sympathetic response to the small drop in mean arterial pressure may already be in effect before further pooling can occur. In a warm environment, where the arterioles in the skin are more dilated, orthostasis leads to faster transfer of blood from the thoracic pool to the legs ![]() N25-4 so that—before the sympathetic response can develop—the initial decreases in stroke volume, mean arterial pressure, and pulse pressure can be large. Thus, soldiers standing quietly at attention in hot weather are more likely to faint than are soldiers marching in a cold environment because of differences in muscle pump activity and vasoconstriction.
N25-4 so that—before the sympathetic response can develop—the initial decreases in stroke volume, mean arterial pressure, and pulse pressure can be large. Thus, soldiers standing quietly at attention in hot weather are more likely to faint than are soldiers marching in a cold environment because of differences in muscle pump activity and vasoconstriction.
As discussed on page 565 , the contraction of skeletal muscle in the legs (the “muscle pump”—see Fig. 24-6 ) drives blood from the large veins in the lower limbs toward the heart. Conversely, each time these skeletal muscles relax, the vascular bed in the legs refills from the arterial side. Obviously, the arteriolar inflow resistance influences the rate at which the veins in the leg refill subsequent to the action of the muscle pump. When the lower limbs are at a high temperature, the arterioles dilate, lowering the inflow resistance and increasing the inflow of blood to the dependent vessels. Therefore, venous pooling worsens at high temperature, which explains why soldiers tend to faint under these conditions.
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here