Diffusion-Weighted Magnetic Resonance Imaging: Principles and Implementation in Clinical and Research Settings

Of the advanced magnetic resonance imaging (MRI) modalities, diffusion-weighted (DW) MRI has probably garnered the most excitement in both clinical and research settings during the past decade. Standard now in nearly every neuroimaging MR protocol, DW-MRI has demonstrated substantial clinical utility in the detection of acute ischemia, the differential diagnosis of intracranial lesions, and the evaluation of white matter. Diffusion tensor imaging (DTI) and other high-angular resolution diffusion imaging (HARDI) models have been applied to the evaluation of normal developmental processes and pathology, particularly that which involves the white matter. Numerous postprocessing methods have been developed that not only allow for group level comparisons of the underlying “tissue microstructure” but also allow for estimation (and visual representation) of the underlying white matter “tracts.” In this chapter, we will review (1) underlying principles of DW-MRI acquisitions; (2) basic diffusion-weighted imaging (DWI) acquisitions (its application in clinical settings); (3) DTI models and postprocessing methods, with emphasis on the strengths and potential pitfalls in both clinical and research settings; and (4) advanced diffusion imaging models.

Underlying Principles of DW-MRI Acquisition

At its core, DW-MRI involves the application of two additional pulses of magnetic field gradient (called “diffusion-encoding” or “diffusion-sensitizing” gradients) to a T2-weighted sequence after the excitation pulse but before the readout. During the first gradient pulse, spin precession is accelerated in accordance with the spatial position of the individual water molecules; spins associated with water molecules with a high Z coordinate, for example, will precess more quickly after administration of a gradient pulse along the Z direction, whereas spins associated with water molecules with a low Z coordinate will precess more slowly. Therefore the net effect of the first gradient pulse on the ensemble of spins is that the spins begin precessing at different rates and consequently “dephase,” resulting in signal attenuation. The second gradient pulse is equal in direction, magnitude, and duration (δ) to the first and is either of opposite polarity (in the case of a gradient echo acquisition) or of the same polarity (in the case of a spin echo acquisition) but placed after a 180-degree refocusing pulse. Assuming that the spins do not move from their original locations, the effect of the second gradient pulse will be to precisely undo the effect of the first and thus “rephase” the spins so there is no longer any signal attenuation due to spin dephasing. However, under physiologic conditions, water molecules possess thermal energy and therefore will move a finite distance away from their original locations during the time between gradient pulses (Δ). Thus, the rephasing is incomplete and the signal will be attenuated compared with the signal with no diffusion-sensitizing gradients.

Assuming that the movement of water molecules is not hindered by any form of barrier (so-called “free diffusion”), the mean squared distance that the spins will move over a given period is described by the Einstein-Smoluchowsky equation and is linearly proportional to the time (Δ) and to the self-diffusion coefficient D . The amount of attenuation is a function of the gradient strength G , gradient duration δ, time between gradient pulses Δ, and diffusion coefficient D . Typically G , δ, and Δ are combined to derive the “b-value”; the higher the b-value, the greater the signal attenuation in the resultant DW images ( Fig. 26.1 ). In fact, signal attenuation is exponential, where S is the measured signal and S ₀ is the signal in the absence of diffusion weighting. As a result, D (measured in mm ² /s) can be estimated by obtaining DW images at different b-values or by obtaining images with and without diffusion weighting.

However, the diffusion of water molecules in the brain differs in two important respects from free diffusion. First, the diffusion of water is hindered by a variety of barriers, including axon sheaths and glial cell and astrocyte membranes. Hence the measured diffusion coefficient is not a self-diffusion coefficient and therefore is referred to as an apparent diffusion coefficient (ADC). Furthermore, the diffusion of water in the brain is not isotropic (i.e., independent of direction). For instance, diffusivity along an axon direction will be larger than diffusivity perpendicular to the axon. Hence, DW images often are obtained using a variety of gradient directions to infer information about the diffusivity of water molecules in different directions; the amount of attenuation in the DW images is dependent on the diffusion of water molecules only in the direction of the applied diffusion-encoding gradients.

It also is important to note that, because DW measurements reflect an attenuation of signal at a given spatial location, maintenance of sufficient signal to noise in the resultant data is an inherent challenge in DWI. Moreover, the time needed to acquire data sufficient for some of the most advanced postprocessing techniques, which require acquisitions at many different gradient direction and b-values, is often well outside of what is typically feasible in clinical settings and in many pediatric populations. Thus in practice, most pediatric DW-MRI studies generally are limited to the more basic DW-MRI models (i.e., DTI, described in a later section of this chapter), although recent developments provide hope that other techniques will become clinically feasible.

Diffusion Weighting, Apparent Diffusivity, and Their Application in Clinical Settings

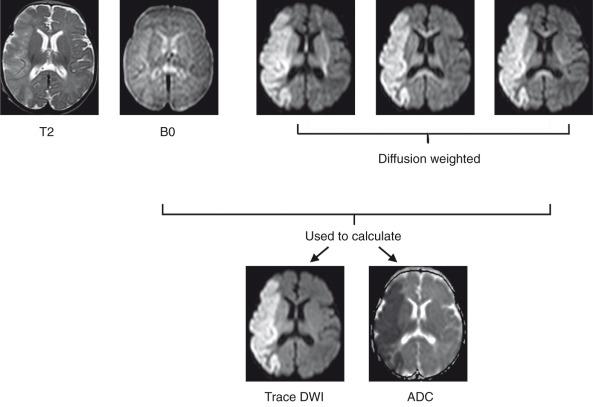
Clinically relevant information is available even from a single DWI acquisition. For instance, diffusion is restricted in regions of cytotoxic edema after a stroke, and these regions therefore will be hyperintense on DW images. However, typical DWI acquisitions are strongly T2-weighted, because a long echo time is necessary as a result of the time needed to apply the diffusion-sensitizing gradients. Therefore it is important to distinguish hyperintensity on DWI that represents true diffusion restriction from hyperintensity that reflects tissue T2 prolongation (often termed “T2 shine-through”). This differentiation usually is performed by the additional acquisition of an image without diffusion weighting (e.g., b = 0 s/mm ² ) and quantifying ADC on a pixel-by-pixel basis, which subsequently can be represented in gray scale as an ADC map. Additionally, instead of a single DW acquisition, three DW images typically are acquired using three orthogonal gradient directions, and the results are averaged to obtain directionally averaged DW images and ADC maps to minimize the effects of anisotropy. The directionally averaged ADC map is proportional to the trace of the diffusion tensor (described later), and thus the DWI images and ADC maps often are referred to as “trace-weighted DWI” and “trace diffusion tensor maps,” respectively ( Fig. 26.2 ).

As previously noted, in the past 2 decades, trace DW images with corresponding ADC values have demonstrated remarkable clinical utility in the detection of cerebral ischemia, before such injuries become apparent on T2-weighted MRI. Acutely, ischemia leads to energy failure, and more specifically, a failure of the Na+/K+–adenosine triphosphatase pumps in the cell membrane. This phenomenon, in turn, leads to an influx of sodium (and other ions) and water into the cell, resulting in cytotoxic edema and a concomitant decrease in ADC.

ADC values decrease within minutes after the onset of cerebral ischemia and reach a nadir around 3 days after onset, although this timing can be variable depending on the magnitude of initial insult, tissue reperfusion, and application of neuroprotective therapies (e.g., therapeutic hypothermia). Subsequently, ADC values begin to rise, reaching “normal values” approximately 1 week after onset (i.e., pseudonormalization) and then continuing higher in the subacute/chronic phase, paralleling cell death and the resultant decrease in cell density.

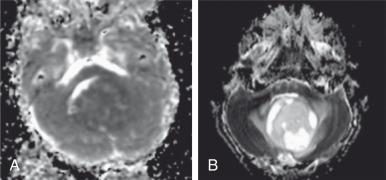
Because ADC is not only sensitive to edema but also cell density, DWI is becoming the method of choice for imaging cancerous lesions. DWI has advantages over positron emission tomography (PET) in that it does not use ionizing radiation or require injection of any radioactive tracer. Water diffusion decreases as cellularity increases; thus a low ADC is usually associated with a high degree of malignancy ( Fig. 26.3 ). By contrast, high ADC values are typically observed in low-grade lesions or in association with a positive treatment response. Recent studies have now combined serial ADC measurements with quantitative postprocessing techniques (i.e., parametric response mapping), which not only allow treatment response to be characterized on a voxelwise basis but also provide quantitative biomarkers for use in clinical trials and in clinical practice.