Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Vaccines are given to people to protect them against disease. They are also given to reduce transmission of infection, thereby preventing disease even in nonvaccinated persons, and thus protecting communities. The extension of perspective from individuals to their communities is the business of public health. The use of an increasing number of different vaccines, in all populations of the world, represents a major, evolving, and highly complicated intervention into human ecology.
For the past several decades, this subject has been discussed largely with reference to the concept of herd immunity , a term that refers to the prevalence or proportion of immune persons in a population, but that is often used with reference to indirect protection of nonimmune individuals, attributable to the presence, and proximity of immune individuals (in effect by the vaccine-derived protection of those who would otherwise infect them). – Much of the discussion has concentrated on the issue of threshold levels of immunity, which, if achieved and maintained, should lead to the decline and ultimate elimination of an infection from a population. Although this is clearly of theoretical interest and public health importance, the emphasis on such thresholds has turned attention away from other, more important, community implications of vaccination programs. In recognition of this, the editors of this volume suggested a broadening of the scope of this discussion, under the term community protection . The phrase is appropriate insofar as individuals can be protected by vaccines without being themselves immune, through reduced community transmission. In this context it is important to acknowledge, at the outset, that both individual and community protection may also be achieved through the direct and indirect effects of other interventions, including social distancing, drugs, education, and environmental changes, which are beyond the scope of this chapter and book.
The shift in perspective from the individual to the community raises many programmatic issues about vaccination, including schedules, consent, “hesitancy”, contraindications, legal enforcement and exemptions, access, public versus private providers, fixed versus mobile services, routine versus targeted programs, campaigns, coverage, monitoring, and evaluation. Many of these issues are covered with respect to particular vaccines and programs elsewhere in this volume. Here we consider more general issues concerning the distribution and implications of vaccine-derived immunity in communities. In simplest terms, one might expect disease incidence to be reduced by a factor equal to the product of vaccine coverage and vaccine efficacy. But the real world is not that simple, and, to predict a program’s impact, we must also consider other issues, such as (1) the distribution of vaccines and of disease risk in communities (neither of which is ever uniform or random); (2) the nature of the immunity induced by the vaccine (measured in terms of partial or complete protection against infection, or reinfection, or against disease, or even against transmission, as well as its natural boosting or waning over time); and (3) the indirect protection of nonimmune persons by the presence of immune persons (the traditional focus of herd immunity discussions).
The issue of indirect protection of nonimmune persons is central to discussions of community effects of vaccination. Such protection applies to important segments of society: to children too young to have been vaccinated, to immunocompromised or elderly persons who cannot make an adequate immune response, to persons with contraindications to vaccination, to persons in whom vaccine-induced immunity was incomplete or has waned, and to those who are unvaccinated, either by choice or because they do not have adequate access to vaccines. The social benefits of such indirect protection have important policy implications, including provision of a rationale for mandating immunization. It provides a justification for the vaccine injury compensation program in the United States: a child who is vaccinated is not only deriving direct protection but is also helping to protect the community; hence, society has some obligation for any injuries incurred by the vaccination. In addition, it is important in determining the full costs and benefits of immunization policies. As new vaccines have become increasingly costly, issues of indirect protection benefits become increasingly important in determining whether to introduce new vaccines and to whom they should be given. The community implications of indirect protection are indeed broad.
After a brief historical review, this chapter summarizes the theory and experience that have evolved to describe various aspects of community immunity, and then considers these principles with reference to major vaccines in use today.
Although both Jenner and Pasteur recognized explicitly the potential of vaccines to control and even to eradicate specific infections from populations, neither is known to have considered the practical issues involved in the application of vaccines to populations. Smallpox vaccination was introduced widely in Europe and North America during the early 19th century, with increasing success over time. Its enforcement through legislation would have long-lasting effects on public acceptance of vaccines, including the appearance of the first antivaccination sentiment opposed to this intrusion by states into the bodies of their citizens. This remains a major issue today. Close observers noted interesting implications of vaccination—for example, William Farr commented as early as 1840, “The smallpox would be disturbed, and sometimes arrested, by vaccination which protected a part of the population,” probably the first recorded recognition of indirect protection by vaccines.
The early years of the 20th century saw important advances in our understanding of the dynamics of infections in populations as a function of the balance of infectious, susceptible, and immune individuals. Several factors contributed to this—in particular, an increased understanding of disease patterns in communities, which arose from the introduction of morbidity (in addition to mortality) notification schemes, the growth of immunology as a discipline, and the development of a theoretical framework linking these data and disciplines together.
Though the phrase herd immunity was used in early veterinary literature , the first discussion of the term in a research context appears to have been in a paper published in 1923 by Topley and Wilson, entitled “The spread of bacterial infection: the problem of herd immunity.” This paper described one of a series of classical studies on epidemics of various infections in closely monitored populations of laboratory mice, and introduced the term in this manner: “Consideration of the results obtained during the past five years … led us to believe that the question of immunity as an attribute of the herd should be studied as a separate problem, closely related but in many ways distinct from, the problem of the immunity of an individual host.” They went on to pose an “obvious problem to be solved: Assuming a given total quantity of resistance against a specific bacterial parasite to be available among a considerable population, in what way should that resistance be distributed among the individuals at risk, so as best to ensure against the spread of the disease, of which the parasite is the causal agent”?
Wilson later recalled that the phrase “herd immunity” had been suggested to him in the course of a conversation with Major Greenwood (G.S. Wilson, personal communication, 1981), and Greenwood employed it in his 1935 textbook, Epidemics and Crowd Diseases . Although these authors did not distinguish explicitly between direct and indirect protection stemming from vaccine-derived immunity, later authors picked up the phrase and applied it in particular to the indirect protection afforded to nonimmune persons by the presence and proximity of immune persons.
The population implications of immunization programs became a major issue during the last quarter of the 20th century, in association with the widespread introduction of vaccines in all populations of the world. Discussion was stimulated in particular by the success of the global smallpox eradication program, as well as by the creation in 1974 of the World Health Organization’s (WHO’s) Expanded Program on Immunization, and the setting of targets to “eliminate” or to eradicate several infectious diseases through vaccines: global targets to eradicate polio and to eliminate neonatal tetanus, and national and regional goals to eliminate measles and rubella. These massive efforts encouraged a body of theoretical literature exploring the population implications of immunization programs, including much discussion of the extent of indirect protection by vaccines, and of coverage criteria for eradication of infection. Although much of the initial theory assumed that immunity was a simple property, that individuals were either fully immune or fully susceptible, and that the protection was solid and permanent against both infection and disease, it became increasingly clear during the 1980s and 1990s that this was incorrect, and that different infections and vaccines could induce different degrees of protection against infection, against disease, and even against infectiousness, and that these different sorts of immunity could wane or be boosted over time. More recent research has attempted to measure these different forms of immunity and to incorporate these subtleties into evaluations of immunity at the community level.
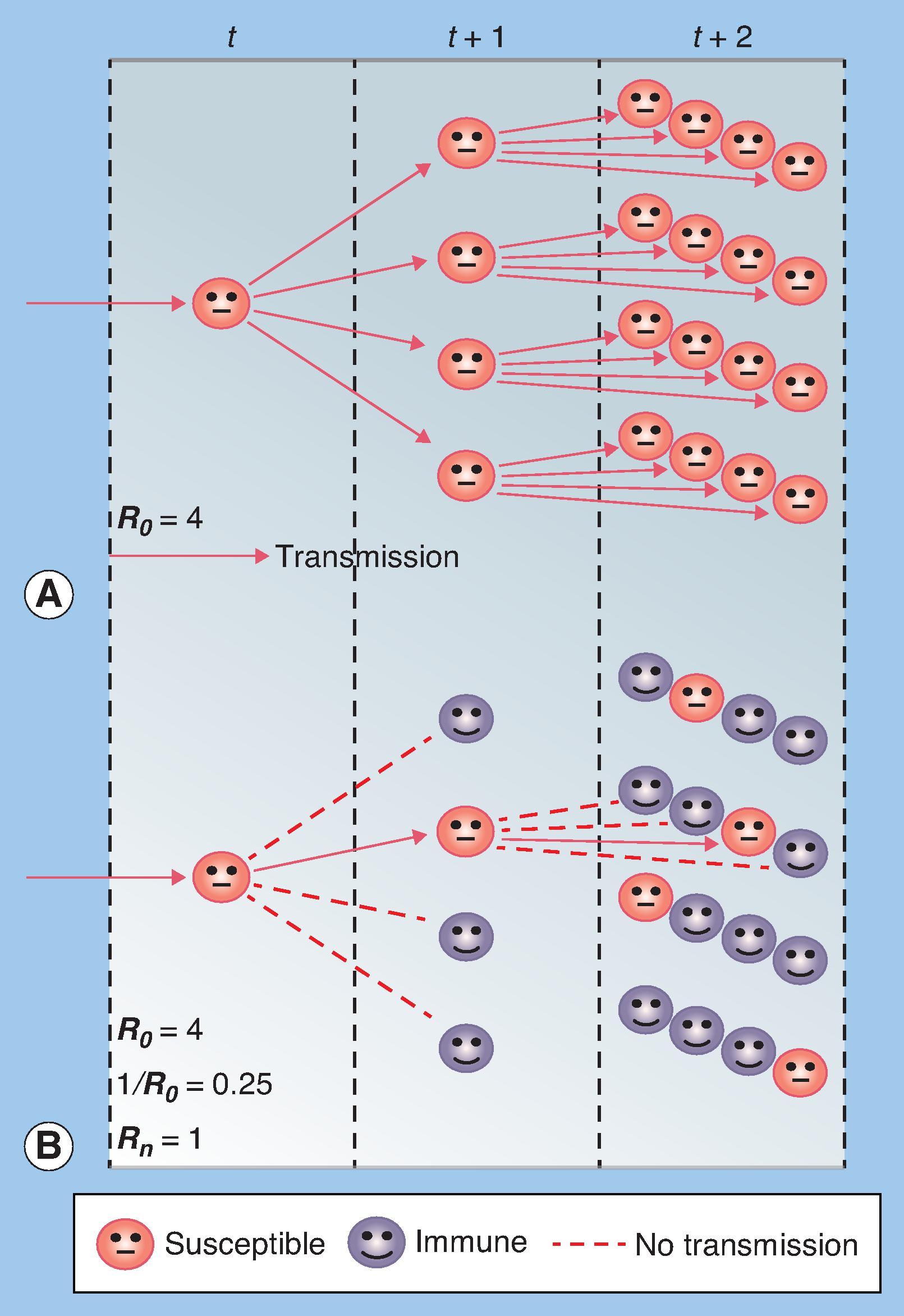
Underlying much of the theoretical work on community immunity has been the recognition that, if an infection or vaccine induces some degree of immunity against infection, then some nonimmune people will be protected indirectly, by the presence and proximity of immune persons, and transmission should stop in a population prior to all individuals becoming immune. This insight encourages the estimation of threshold numbers or proportions of immune individuals necessary for this cessation to occur. An elegant body of theory has evolved around this issue, developed initially to describe the implications of introducing fully immune people into randomly mixing populations, but subsequently extending to more realistic scenarios.
Fig. 78.1 illustrates (very simply) the principle of indirect protection by showing susceptible and immune individuals in a population, with arrows indicating the spread of an infection. Actual transmission patterns depend on the distribution of susceptible individuals in space and time (social mixing patterns), and some susceptible individuals may be shielded from infection by being surrounded by immune individuals. Representations such as Fig. 78.1 fail to show that, even if there were no immune individuals at the start of an outbreak, infections may generate immune individuals who can in turn block transmission and lead to termination of an epidemic before all individuals become infected. We thus need to consider dynamics.

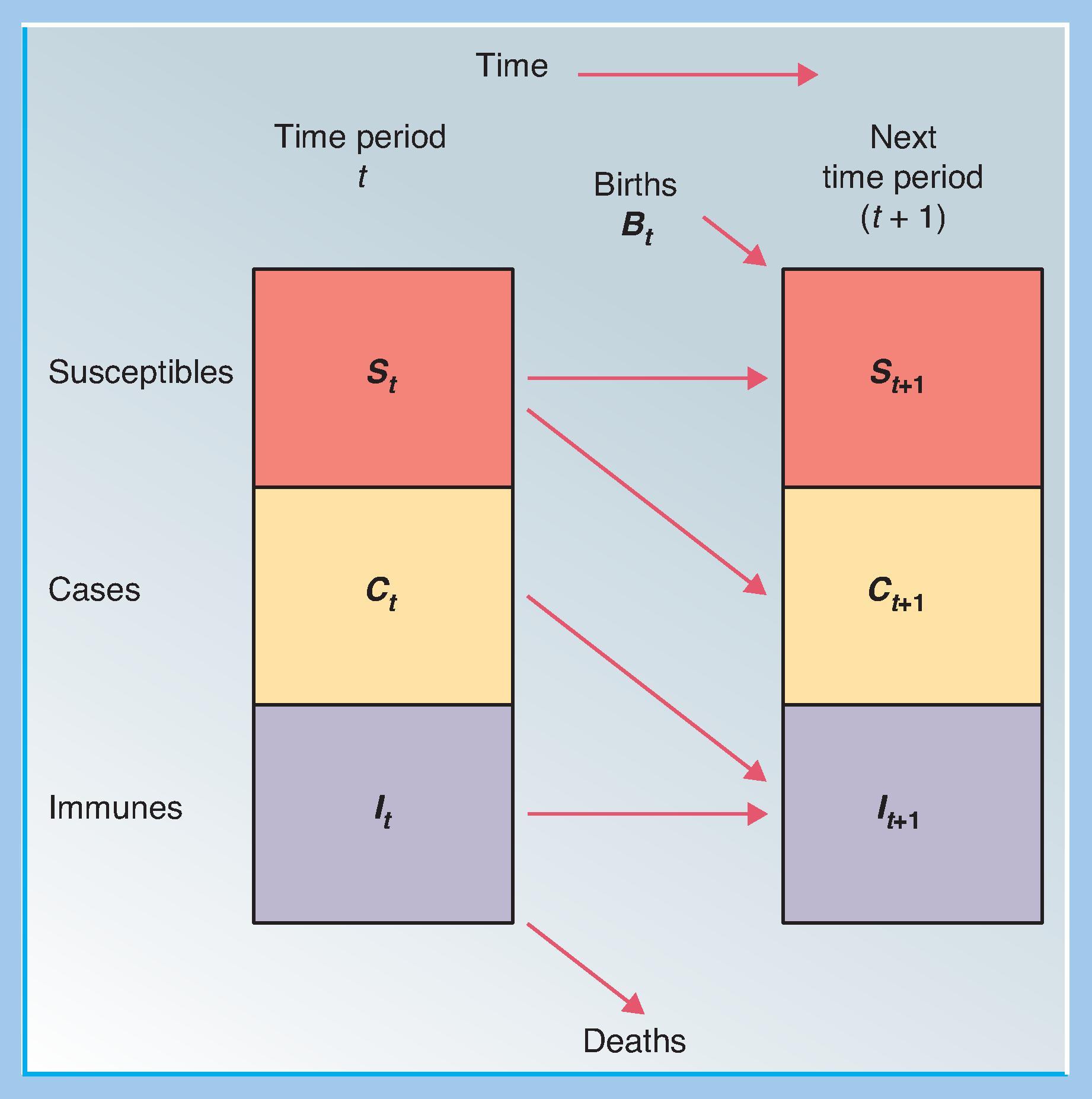
The crucial argument was introduced in 1906, by William Hamer, in the context of a discussion of the dynamics of measles in London. He argued that the number of new cases ( C t + 1 ) in a time period equal to the serial interval of the infection (thus one generation of cases, or approximately 2 weeks for measles) is a function of the product of the numbers of infectious cases and of susceptible persons in the previous time period ( C t and S t , respectively; Fig. 78.2 ). In simple terms,
where r is a transmission parameter, or contact rate—in effect, the proportion of all possible contacts between susceptible and infectious individuals that lead to new infections (so, r ≪1). For example, if there are 10 cases and 90 susceptibles, there are 900 possible connections between cases and susceptible individuals. The transmission parameter r is the proportion of those possible contacts resulting in transmission and new cases. To simulate successive changes over time, the number of susceptible individuals is recalculated for each new time period as
where S t + 1 is the number of susceptible individuals in the next time period and B t is the number of new susceptible individuals added (e.g., born into) the population per unit time. (Note that bold symbols are used in this chapter to denote numbers of individuals, and nonbold symbols to denote proportions or other descriptive statistics [ Table 78.1 ]). The relationship in Eq. (78.1) , that future incidence is a function of the product of current prevalence and current numbers susceptible, is known as the epidemiologic “law of mass action,” by analogy with the physico-chemical principle that the rate of a chemical reaction is a function of the product of the concentrations of the reactants. Often expressed as a differential (continuous time) rather than a difference (discrete time) equation, as here, this relationship underlies much theoretical work on the dynamics of infections in populations. Note that Eqs. (78.1) and ( 78.2 ) include no explicit term for immune individuals. By implication, deaths prior to infection are not considered in this simplest model (i.e., in each period, the same number of immune individuals die as susceptible people are born into the population). The introduction of terms for immune individuals; for individuals incubating the infection; for population growth and selective mortality of susceptible, infected, and immune individuals; and for age, is explored at length in the literature, but the additional terms do not change the basic message emphasized here. ,
| Symbol * | Variable Definition |
|---|---|
| C t , C t +1 | Numbers of cases in successive serial intervals |
| S t , S t +1 | Numbers of susceptible individuals in successive serial intervals |
| I t , I t +1 | Numbers of immune individuals in successive serial intervals |
| B t | Number of new susceptible individuals (i.e., births) per serial interval |
| r | Transmission parameter for the simple mass action model, interpretable as the proportion of all possible contacts between cases and susceptible individuals that lead to new infections |
| S E | Epidemic threshold number of susceptible individuals (if exceeded, incidence increases) |
| T | Total population size |
| H | Herd immunity threshold (proportion of immune individuals in a population required to lead to decline in incidence): H = 1 – S E / T = 1 – 1/ R 0 |
| R 0 | Basic reproduction number (average [expected] number of secondary cases attributable to a single case introduced into a totally susceptible population) |
| R n | Net reproduction number (actual number of transmissions per case) |
| S | Proportion of susceptible individuals in a population |
| A | Average age at infection in years |
| L | Average life expectancy in years |
| U | Vaccine coverage (“uptake”) |
| U H | Vaccine coverage (uptake) to achieve herd immunity threshold |
| P | Protective efficacy of vaccine (proportion protected among vaccinees) |
| P i | Protective efficacy of vaccine in terms of susceptibility to infection (proportion of vaccinees who are rendered nonsusceptible to infection) |
| P t | Protective efficacy of vaccine in terms of transmissibility (proportion of vaccinees who fail to shed organisms despite becoming infected) |
* Bold symbols represent numbers of individuals. Nonbold symbols represent proportions or other descriptive statistics.
Fig. 78.3 shows what happens when Eqs. (78.1) and ( 78.2 ) are iterated, and serves to illustrate several principles of the epidemiology of those acute immunizing infections, such as measles, mumps, rubella, chickenpox, poliomyelitis, and pertussis, that affect a high proportion of people in unvaccinated communities. First, the model predicts cycles of infection incidence, which are well recognized for many of the ubiquitous infections of childhood ( Fig. 78.4 ). The incidence of infection rises above and dips below the birth rate, or the rate of influx of new susceptible individuals. Second, the number of susceptible people also cycles, around a number that is sometimes described as the epidemic threshold ( S E ). Rearrangement of Eq. (78.1) to C t + 1 / C t = S t × r reveals that this threshold number of susceptible persons is numerically equivalent to the reciprocal of the transmission parameter r , as incidence increases (i.e., C t + 1 > C t ) when, and only when, S t > 1/ r , and thus S E = 1 /r . In the example illustrated in Fig. 78.3 , r = 0.0001 and S E is thus 10,000. The correspondence between the case and susceptible lines in the figure illustrates this relationship: whenever case incidence exceeds the birth rate, the number of susceptible people falls (as it must), and vice versa. Also, whenever the number of susceptible people rises above the epidemic threshold, incidence rises, and vice versa.


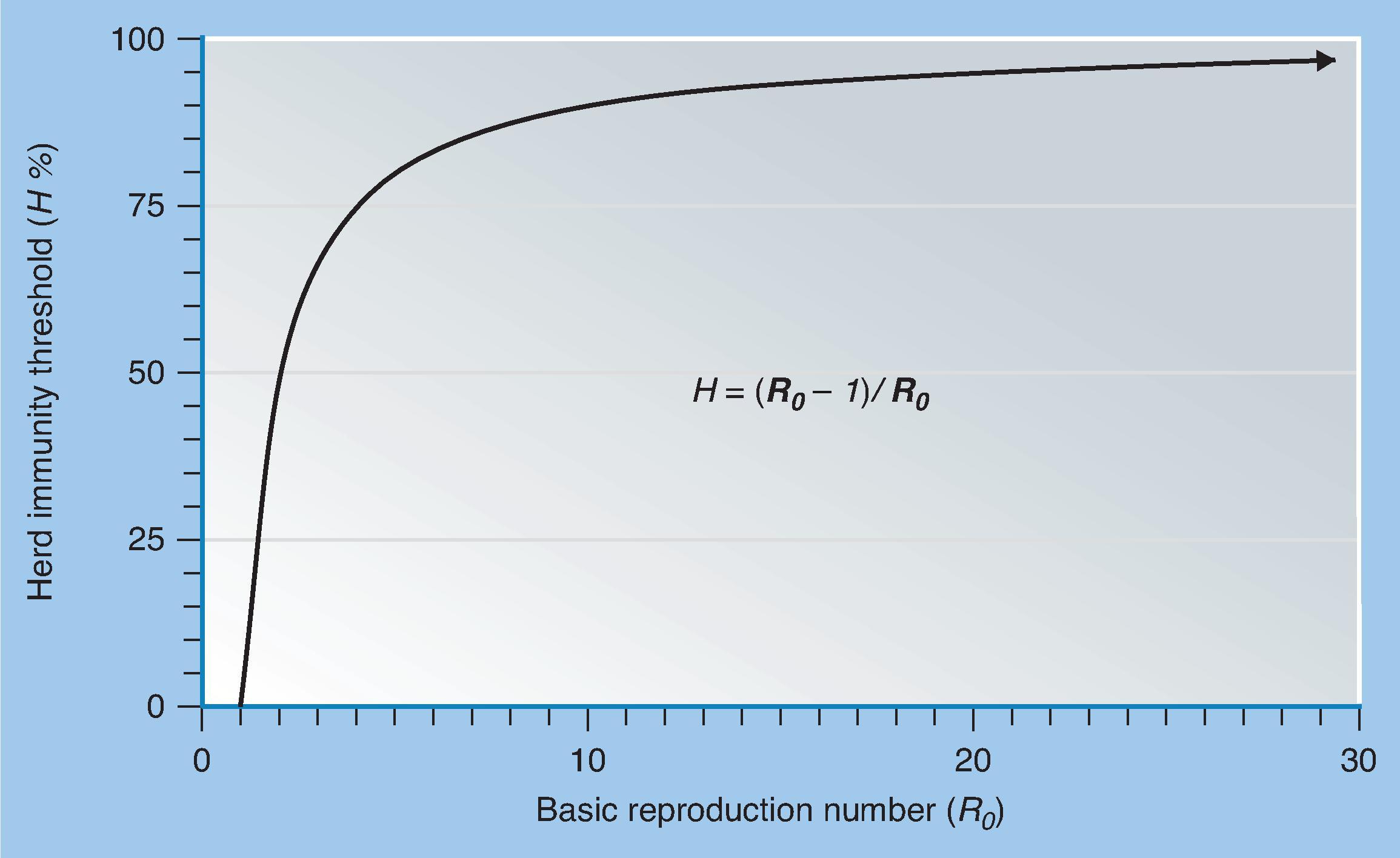
This epidemic threshold implies a simple herd immunity criterion. If the proportion immune is so high that the number of susceptible people is below the epidemic threshold, then incidence will decrease. We can express this threshold algebraically as follows:
where T is the total population size, S E is the epidemic threshold number of susceptible people for the population, S E / T is the proportion susceptible at the threshold, and H is the herd immunity threshold—that is, the proportion of immune individuals in the population that must be exceeded if incidence is to decrease. If the total population in the Fig. 78.3 example were 100,000, this would imply a herd immunity threshold ( H ) equal to 1−10,000/100,000 = 1−1/10, or 90%.
We can approach this herd immunity concept from an alternative, and equally informative, perspective. If an infection is to persist, each infected individual must, on average, transmit the agent to at least one other individual. If not, incidence will decline and the infection will disappear progressively from the population. The number, or distribution, of actual onward transmissions per case thus describes the spread of an infection in a population, and it is a function of four things: (1) the duration of infectiousness; (2) the likelihood of transmission per “contact” between infectious and susceptible individuals; (3) the rate and pattern of contact between members of the host population; and (4) the proportion susceptible in the host population. Its value under any set of circumstances is known as the “reproduction number” of the infection, by analogy with standard demographic measures (the average number of progeny per individual per generation). This average number of actual transmissions should be at a maximum if all members of the host population are susceptible—in which circumstance it is known as a basic reproduction number ( R 0 ) , defined formally as the average number of transmissions expected from a single primary case introduced into a totally susceptible population. This definition can be translated directly into the mass action formulation ( Eq. 78.1 ) by setting C t = 1 and S t = T , to represent the single case introduced into a fully susceptible population. The number of secondary cases, C t + 1 , is then equivalent, by definition, to the basic reproduction number ( R 0 ):
This basic reproduction number describes the maximal spreading potential of an infection in a population. Continuing with the example in Fig. 78.3 , the introduction of a single primary case into the population of T = 100,000 susceptible persons should lead to 10 secondary cases ( C t + 1 =100,000 × 0.0001 = 10 = R 0 ). Table 78.2 shows examples of numerical values of this statistic that are applicable to different infections and derived by methods described below. Fig. 78.5A is an illustration of the concept.
| Infection | Basic Reproduction Number ( R 0 ) | Crude Herd Immunity Threshold, H (%) |
|---|---|---|
| Covid-19 Ω | 2.5–5 | 43–80 |
| Diphtheria ∆ | 6–7 | 83–85 |
| Influenza ‡ | 1.4–4 | 30–75 |
| Measles | 12–18 | 92–94 |
| Mumps | 4–7 | 75–86 |
| Pertussis ‡‡ | 5–17 | 80–94 |
| Polio # | 2–20 | 50–95 |
| Rubella | 6–7 | 83–85 |
| Smallpox | 5–7 | 80–85 |
| Tetanus | Not applicable | Not applicable |
| Tuberculosis ¶ | ? | ? |
| Varicella ** | 8–10? | ? |
* Herd immunity threshold ( H ), calculated as 1–1/ R 0 or by epidemic growth trajectory.
† The values given in this table are approximate and crude; they do not properly reflect the tremendous range and diversity among populations, nor do they reflect the full immunologic complexity underlying the epidemiology and persistence of these infections. See text for further discussion.
Ω A range of R 0 values have been estimated (increasing with recent variants), and a variety of herd immunity thresholds calculated based upon different assumptions about population mixing and susceptibility. It is now known that immunity to infection with Covid-19 is not solid, and wanes with time.
∆ Complicated by fact that vaccine-derived immunity relates to toxin, not to infection.
‡ R 0 of influenza viruses probably varies greatly between subtypes.
‡‡ Note that immunity to B pertussis infection is not solid, but wanes over time.
# Complicated by uncertainties over immunity to infection and variation related to hygiene standards. ¶Protective immunity not defined.
** Immunity not sterile; herd immunity threshold not defined. These estimates drawn from references 1, 14, and publications cited in specific disease sections of this chapter.
If immune individuals are present in a population, then some of the contacts of infectious individuals will be with these immune individuals, and hence will fail to lead to transmission. As a result, the average number of actual infection transmissions per case will be less than the basic case reproduction number, and this has been defined as the net, or actual, or effective, reproduction number ( R n ). – This actual number of transmissions ( R n ) should be equivalent to the basic case reproduction number ( R 0 ) times the proportion susceptible in the population ( S ):
By this expression, if the proportion susceptible ( S ) were equal to the reciprocal of the basic reproduction number of the infection (1 / R 0 ), the average number of transmissions per case ( R n ) should be 1, and thus incidence should remain constant over time. Fig. 78.5B illustrates this, and it once again leads us directly to the herd immunity threshold ( H ). Because the proportion immune is just the complement of the proportion susceptible ( H = 1 − S ), we have:
The same expression can also be derived just by combining Eqs. (78.3) and ( 78.4 ). As long as the proportion immune is maintained above this threshold, incidence should decrease, ultimately to the point of elimination of the infection from the population. Fig. 78.6 shows the relationship graphically, which shows the implications for persistence or decline of an infection depending on its basic reproduction number and the proportion of individuals who are immune in the population. , , , ,
Given this theoretical relationship between the basic reproduction number of an infection in a population and the herd immunity threshold, the estimation of R 0 becomes an important challenge. If the infection is so common that it affects virtually everyone in unvaccinated populations, as is the case with many of the acute immunizable diseases of childhood (e.g., measles, mumps, rubella, and polio), one derivation of R 0 turns out to be relatively straightforward. According to the logic described above, R 0 is equivalent to the reciprocal of the average proportion susceptible in the population over an epidemic cycle (see Eq. 78.5 and Fig. 78.5 B; note that the proportion susceptible cycles around S E / T = 1 − H , as in Fig. 78.3 and Eq. 78.3 ). Dietz pointed out that for immunizing infections the proportion susceptible is approximated by the average age at infection ( A ) divided by the average life expectancy in years ( L ), and thus R 0 ≈ L/A . He went on to show that, for populations with exponential age structures (typically found in low-income countries), a better estimate of R 0 can be obtained with the following equation:
Another method of estimating R 0 , used in particular for influenza, and new infections such as COVID-19, is based on an analysis of the rate of increase in incidence in the early phase of an epidemic with a new virus. In theory, incidence should increase by a factor equal to R 0 each generation, or serial interval (the time between successive cases in a chain of transmission, approximately 3 days for influenza and 6 days for COVID-19). The effective reproduction number can also be estimated by this approach, if there is prior immunity in the population—and with knowledge of the fraction susceptible, it may then be possible to estimate R 0 , although this latter step is typically more difficult. Detailed discussion of the estimation of R 0 by these and other methods can be found in several references. , , , The herd immunity thresholds cited in Table 78.2 are based on these values, and provide crude estimates of the proportions of immune persons required, in theory , to eliminate these infections. As discussed below, and emphasized repeatedly in this chapter, these thresholds, even though widely cited, are based on unrealistic assumptions (solid immunity, homogeneity, random mixing) and should only be used as a very rough guide.
R 0 is a standard measure of the transmissibility of an infection, and hence of the potential rapidity of its spread in a population, per generation, or serial interval, of the infection. This can have very different real time implications, depending on whether the serial interval is relatively short (e.g., approximately 3 days for influenza) or relatively long (e.g., approximately 15 days for a measles-like infection). , Although the R 0 of influenza is appreciably smaller than that for measles (i.e., about 2 vs about 14) (see Table 78.2 ), influenza can go through 10 generations within a 30-day month whereas measles can go through only two generations, implying 2 10 = 1024 new cases of influenza at the end of the month compared with only 14 2 = 196 for measles, if the populations were 100% susceptible at the start of each outbreak. (These are just illustrative numbers; of course, the increase in the number of immune persons would slow down the spread.) Despite this more rapid spread of influenza in a virgin population, consideration of the R 0 values shows that influenza should be more easily brought under control than measles: the herd immunity thresholds being H = 50% for influenza versus H = 93% for measles infection, assuming an R 0 for influenza of 2 and for measles of 14. This distinction has received much attention in recent discussions of the feasibility of controlling pandemic influenza. ,
The elegant theory just summarized is built on extreme assumptions: that all individuals mix at random, that individuals are either fully susceptible or fully immune, and that the population is uniform (i.e., that all individuals behave the same way and all infected individuals are equally infectious). These assumptions are unlikely to hold for any infection in any human population. There has thus been an effort to adapt the theory to more realistic assumptions, including heterogeneity of mixing patterns and of susceptibility and infectiousness.
The first attempt to consider the implications of population heterogeneity for herd immunity appeared in a 1971 paper by Fox et al., entitled “Herd immunity: basic concept and relevance to public health immunization practices.” This paper, for many years the most frequently cited article on herd immunity, took a very different approach from that reviewed above, and was based on simulation rather than on analytic argument. The authors set up a population of 1000 people, divided into family, school, and social groupings, and assigned different contact rates within and between these groups. Importantly, they did not consider age, nor did they consider an influx of susceptible persons into the population (the B t term in Eq. 78.2 ). Their approach was thus applicable only to closed populations, and they were unable to address the larger issues of infections in dynamic populations. , Although the approach precluded estimation of a herd immunity- threshold, it provided a first glimpse of the epidemiologic complexity inherent in heterogeneous populations, and it led the authors to be skeptical of simplistic notions of herd immunity.
Subsequent workers have used a variety of analytic and computer simulation approaches to explore more realistic assumptions than those underlying the simple mass action theory. In particular, there has been exploration of the important implications of age, leading to elegant methods for estimating R 0 based on a description of different age-specific contact rates set out in a “who-acquires-infection-from-whom” (WAIFW) matrix. , These methods have provided formal arguments demonstrating the need to vaccinate as early in life as possible after maternal immunity has waned and before exposure to natural infections. These studies have allowed exploration of the effects of various vaccination strategies on the age distribution of infection—in particular, how low or moderate levels of vaccine coverage among infants or young children will change the dynamic equilibrium, slowing down transmission, and thereby leading to an increase in the average age at infection among those who fail to be immunized by the vaccine. These effects are particularly important for infections whose seriousness increases with age, such as rubella and, to a lesser extent, mumps, chickenpox, or polio. , For any vaccination program that targets one age group (often young children) but which may impact others (e.g., the elderly) the pattern of contact between groups will be critical. To help predict these effects, a number of studies of contact patterns have been performed, the largest and most influential to date being the POLYMOD study, which documented contact patterns across eight European countries. This study found remarkable consistency across Europe in the patterns of age-dependent mixing, with contacts being typically “assortative” (like with like), particularly in children and young adults.
There are many other forms of heterogeneity in human populations—in particular, geographic and social groupings—all of which have subtleties and are likely to confound one another, because different social groups tend to have different age and spatial patterns. Social groups may be separate or may overlap (e.g., neighborhood and occupational or school groupings) in different ways in different societies, and they may be associated with environments or behaviors that either encourage or discourage the transmission of infection. Consideration of such heterogeneities in simulation models has demonstrated that it is generally more efficient to target high-risk versus low-risk groups with vaccines, in the sense that the number of cases of disease prevented is greater per single vaccination in a high-risk than in a low-risk population. , However, a real vaccination program might be unwise to emphasize such a strategy, because of issues of social equity, and also because evidence shows that, in the absence of eradication, susceptible people continue to accumulate in the less-served areas, and population mobility continues to seed virus into such populations. According to yet another perspective, it has been argued that equal allocation of vaccine to high- and low-risk segments of a population will have a greater impact in the low-risk communities, and thus might increase health inequalities within the overall population! Table 78.3 summarizes the implications of these several heterogeneities for the simple herd immunity threshold values as shown in Table 78.2 .
| Variable and Assumption | Implications for Herd Immunity Threshold | References |
|---|---|---|
| Vaccination after maternal immunity wanes | If vaccines are not effective until maternal immunity wanes, crude H estimates based on ages from birth will be low. This can be corrected by considering that a child is not born until maternal immunity disappears. | |
| Timeliness in age at vaccination | Herd immunity effect is greatest ( H threshold lowest) when vaccination occurs at the earliest possible age. Delayed vaccination implies that threshold coverage level will be higher than simple estimates. | , , |
| Age differences in contact rates or infection risk | Implications vary with relationship between age and contact rate. Falling contact rates with age implies that true H may be lower than simple global estimate. | , |
| Seasonal changes in contact rates | Seasonality may imply lower herd immunity threshold if seasonal change is marked, and fade-out can occur during low transmission period. | |
| Geographic heterogeneity | In theory, geographic differences in contact rates may permit elimination with lower overall vaccine coverage than that implied by H based on total population, by targeting high-risk groups. | |
| Social structure (nonrandom mixing) | Social structure can have complicated implications because it implies group differences in vaccination uptake and infection risk. Existence of vaccine-neglecting high-contact groups means true H will be higher than simple estimates. This effect can be very large. | , (and others) |
On a more practical level, the nonuniformity of populations is used commonly either to target vaccines at high-risk groups or to facilitate widespread vaccine coverage. Thus, the selective use of varicella vaccine in nurses or family members reduces the likelihood of varicella transmission to immunosuppressed patients. The targeting of hepatitis B vaccine in prisons provides protection to a population at high risk through intravenous drug use. Several European countries now recommend bacille Calmette-Guérin (BCG) vaccine only to high-risk communities, and school-based programs have been widely used in many countries to access large numbers of children. At the time of writing this chapter, there is much discussion of strategies to allocate COVID-19 vaccines so as best to protect particularly vulnerable segments of society.
Thus far, our discussion has implicitly assumed that immunity is one face of a simple binary property—that individuals either are susceptible or they are solidly immune and protected from both infection and disease. For most infections, the real world is not like this at all. We know that immune responses are highly complex, involving humoral and cellular pathways, as well as a variety of cell types and chemical mediators, and that these vary among infections, among individuals, and over time. The epidemiologic implications of this heterogeneity are important.
The conventional epidemiologic measure of immunity induced by vaccination is known as vaccine efficacy , defined as the percent reduction in incidence of disease among vaccinated persons as compared with nonvaccinated, equally exposed controls. It is now recognized that this basic measure of vaccine-derived immunity is itself ambiguous, insofar as 80% efficacy could mean either that 80% of vaccinees are totally protected, by some all-or-none mechanism of protection, or that the vaccine-derived immunity is only “partial,” such that the level of susceptibility in all vaccinated individuals has been reduced by 80%. This distinction has profound implications both for measurement of vaccine effects (e.g., whether it is more appropriate to use risks or person-time rates in calculations) and for our understanding of immunity (e.g., whether certain immune responses are fully protective or only partially so, perhaps more effective against low-dose than against high-dose challenge, or more protective against closely related compared with more distantly related antigenic types of the pathogen). The combined epidemiologic and immunologic implications of the distinction between all-or-none and partial protection are not yet well understood.
It is known that immunity can wane with time, for some infections, and this has obvious importance for community protection and herd immunity thresholds. If not taken into account, estimates of vaccine effects will be over-optimistic. Because of this waning of immunity, boosters are recommended for many vaccines. The rate at which this waning occurs differs between infections and vaccines, being relatively slow for measles, for example, and higher for pertussis. The term boosting is interesting in this context, as there is increasing recognition that immunity to several infections (e.g., varicella, pertussis) is enhanced through repeated natural exposure throughout life. In the absence of natural boosting re-exposures, the risk of reinfection or reactivation disease may increase with time, many years after the first encounter.
Beyond these quantitative differences in immunity, there are also important qualitative differences, dependent on whether, and to what level, any protection acts against infection, against reinfection, against severe or mild disease, or against infectiousness (transmissibility). For some infections (e.g., measles), vaccine-induced immunity may protect similarly against infection and against disease, whereas for others (e.g., inactivated polio, pertussis, diphtheria, rotavirus, SARS-CoV-2), the vaccine-induced protection appears stronger against disease. It also may reduce shedding of the agent by infected persons (e.g., live polio, pertussis). We understand the biologic mechanisms for some of these differences—for example, live oral poliovirus vaccines induce local enteric immunity and hence are more effective against poliovirus infection than are killed, parenterally administered poliovirus vaccines. It is in theory possible to measure these different forms of protection epidemiologically, by collecting data on both infection and disease status of people, and by estimating vaccine efficacy conditional on the vaccination status of both the source and the recipient of potential transmission. Such data are sometimes available, in particular, in the context of household secondary attack rate studies, but their rarity means that most of our epidemiologic measures of immunity overlook these distinctions. This oversight does not mean that the distinctions are unimportant.
Vaccines reduce disease by direct protection of vaccinees and by indirect protection of nonimmune persons. Indirect protection depends on a reduction in infection transmission, and hence on protection (immunity) against infection, not just against disease. If a vaccine were to protect only against disease, and not at all against infection, then it would have no influence on infection transmission in the community and there would be no indirect protection (vaccination of one person would have no influence on any others in the community). It would be possible to reduce disease with such a vaccine but not to eradicate the infection. This is an extreme scenario (although it has been discussed in the context of tetanus, diphtheria, pertussis, and inactivated poliovirus vaccines), but we can explore more plausible circumstances.
We first assume that vaccine-induced immunity is a simple all-or-none affair, such that a proportion ( P ) of vaccinees is fully protected against an infectious agent. If vaccine coverage (“uptake”) is U , then a proportion P × U of the total population will be rendered fully immune. Under these circumstances, from Eq. (78.6) , the coverage required to reach the herd immunity threshold ( U H ), and thereby bring about a sustained reduction in incidence, will be as follows:
If, in contrast, a vaccine can protect to some degree against infection (a proportion P i of vaccinees are rendered no longer susceptible to infection) and can also reduce transmissibility, that is, infectiousness (a proportion P t among those vaccinated persons who do become infected do not shed, or shed fewer, organisms and hence cannot transmit infection), then, as shown by Longini et al., the coverage (“uptake”) required to reach the herd immunity threshold (i.e., to reduce incidence) should be as follows:
This expression is a way of illustrating the importance of vaccine-mediated reductions in infectiousness, as well as in reducing susceptibility to infection. If protection induced by the vaccine against infection ( P i ) and transmissibility ( P t ) are both 100%, this equation reduces to Eq. (78.6) , and the critical herd immunity coverage threshold is just ( R 0 − 1 )/( R 0 ). However, if, for example, the vaccine induced only 60% protection against infection, and 40% protection against transmissibility among those who were infected, the critical coverage threshold to reduce infection incidence should be ( R 0 − 1 )/( R 0 × [0.6 + 0.4 − 0.24]) = ( R 0 − 1)/( R 0 × [0.76]), thus about 4/3 times, or 33% higher, than the simple ( R 0 − 1)/( R 0 ) estimate. One should not expect precision in such estimates, but this result makes intuitive sense. The overall effect of a vaccine in reducing disease incidence in a community will combine these two mechanisms: protection against infection transmission, and direct protection of vaccinees against disease. These properties are important for understanding the effects of several vaccines in common use (e.g., polio, pertussis, diphtheria) and are likely to be even more important for several vaccines currently under development (e.g., malaria, hookworm, HIV).
We turn now to compare the implementation and impact of actual vaccination programs with what was and is predicted by theory, and to highlight a variety of issues raised by particular vaccine-preventable diseases. Readers are referred elsewhere in this text for further details on the infections and vaccines used here as examples.
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here