Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Organization of the Respiratory System
Comparative Physiology of Respiration
External respiration is the exchange of O 2 and CO 2 between the atmosphere and the mitochondria
For millennia, people have regarded breathing as being synonymous with life. Life begins and ends with breathing. The Bible states that God “breathed into [Adam's] nostrils the breath of life” and then later used part of Adam's ventilatory apparatus—a rib—to give life to Eve.
In the fourth and fifth centuries bc , writings attributed to Hippocrates suggested that the primary purpose of breathing is to cool the heart. It was not until the 18th century that the true role of breathing began to emerge as several investigators studied the chemistry of gases. Chemists had recognized similarities between combustion and breathing but thought that both involved the release of a “fire-essence” called phlogiston. According to their theory, neither combustion nor life could be supported once air became saturated with phlogiston.
In the 1750s, Joseph Black 
N26-1 found that heating calcium carbonate produces a gas he called “fixed air,” now known to be carbon dioxide (CO 2 ). He also found that animal respiration produces this gas. Shortly thereafter, Henry Cavendish N26-2 found that fermentation and putrefaction also produce fixed air. The early 1770s saw the codiscovery of oxygen (O 2 ) by Carl Scheele N26-3 (who called it “fire air”) and Joseph Priestley N26-4 (who called it “dephlogistonated air”). In 1785, Henry Cavendish N26-2 found that dephlogistonated air represents ~20% of atmospheric air. Priestley found that combustion, putrefaction, and breathing all consume dephlogistonated air, and all reduce the volume of room air by ~20%. Conversely, he found that green plants produce dephlogistonated air, which he quantitated by reacting it with nitric oxide (a colorless gas) to produce nitrogen dioxide (a red gas).
N26-1
Joseph Black (1728–1799)
Joseph Black, a Scottish physician and chemist, made three landmark discoveries. He discovered the concepts of latent heat and specific heat. Most important for respiratory physiology, he also discovered carbon dioxide (CO 2 ), which he called “fixed air.” In the critical experiments, Black found that either heating or adding acid to calcium carbonate (CaCO 3 ) produced fixed air. This work revolutionized chemistry by showing that other gases exist besides ordinary “air” and that a chemical reaction can involve a gas.
Black also demonstrated the reverse: bubbling fixed air through a solution containing calcium hydroxide caused the precipitation of CaCO 3 . Black used this assay to demonstrate that animal respiration produces fixed air.
For more information about Joseph Black, visit the following websites:
N26-2
Henry Cavendish (1731–1810)
Henry Cavendish is known for recognizing that hydrogen gas ( H 2 , or as he called it, “inflammable air”) is made up of an element. Along with James Watt and Antoine Lavoisier, Cavendish found that inflammable air reacts with oxygen (“dephlogistonated air”) to produce water (Lavoisier did similar work). Cavendish interpreted these data in terms of phlogiston; it was Lavoisier who made the modern interpretation and gave hydrogen its name. Cavendish—along with Joseph Priestly, N26-4 Joseph Black, N26-1 and others—is sometimes regarded as a pneumatic chemist.
Cavendish was not only brilliant but also extraordinarily shy. He made many discoveries that were never published but nevertheless predated the discoveries credited to others (Charles's and Dalton's laws dealing with gases and Ohm's and Coulomb's laws dealing with electricity). For more information about Henry Cavendish, visit the following websites:
N26-3
Carl Wilhelm Scheele (1742–1786)
Carl Scheele was a Swedish pharmacist and chemist who made several important discoveries in the early history of chemistry. Unfortunately, many of his key discoveries were published after those of his competitors. He died at an early age, apparently from the toxic effects of the chemicals that he studied.
Scheele obtained what he called “fire air” in 1771, first from manganese dioxide (MnO 2 ) and then from HgO and other oxygen-containing compounds. Priestley obtained “dephlogistonated air” from HgO in 1774.
For more information about Scheele, visit the following websites:
N26-4
Joseph Priestley (1733–1804)
Joseph Priestley was a theologian, philosopher, and chemist who—along with Carl Wilhelm Scheele—is generally credited with the discovery of oxygen (O 2 ), which he called “dephlogistonated air.” In his key experiment, which dates from 1774, Priestley focused the sun's rays on mercuric oxide (HgO), producing dephlogistonated air. Moreover, Priestley showed that dephlogistonated air was 5- to 6-fold more effective at supporting breathing or combustion than “common atmospherical air.”
Carl Wilhelm Scheele N26-3 discovered a gas that he called “fire air” (O 2 ), probably in 1771 (i.e., 3 years before Priestley). However, Scheele's work was not published until 1777. Scheele obtained fire air first from manganese dioxide (MnO 2 ) and then from HgO and other oxygen-containing compounds.
Priestley was a staunch supporter of the phlogiston theory; it was Antoine Lavoisier N26-5 who put the observations of Priestley on sound theoretical grounds.
Priestley's political views (e.g., supporting the American and French Revolutions) and religious views (e.g., supporting religious dissent and contributing to the founding of the Unitarian Church) forced him to flee to America, although not before his home was burned by rioters. He spent the last 10 years of his life in rural Pennsylvania, never having putting aside the phlogiston theory.
For more information about Priestley, visit the following websites:
In the mid-1770s, Priestley presented his findings to Antoine Lavoisier N26-5 —often regarded as the father of modern chemistry. Lavoisier quickly put Priestley's empirical observations into a theoretical framework that he used to demolish the phlogiston theory, which Priestley held to his death. Lavoisier recognized that dephlogistonated air, which he named “oxygen,” represents the ~20% of room air consumed by combustion in Priestley's experiments, leaving behind “nonvital” air, or nitrogen (N 2 ). Furthermore, he proposed that O 2 is consumed because it reacts with one substance to produce another. The mathematician Joseph-Louis Lagrange N26-6 suggested that O 2 consumption and CO 2 production occur not in the lungs but in isolated tissues, as Lazzaro Spallanzani later rigorously demonstrated in the late 18th century. N26-7
N26-5
Antoine Lavoisier (1743–1794)
Antoine-Laurent de Lavoisier—known simply as Antoine Lavoisier after the French Revolution—was a French nobleman who is sometimes regarded as the father of modern chemistry. He did not make any discoveries of chemicals to which others could not also lay claim (e.g., hydrogen gas in the case of Cavendish N26-2 ), nor develop any highly novel experimental apparatus. Rather, his contributions were mainly theoretical, supported by quantitative experiments that extended the work of others (e.g., Black, Scheele, Priestley, Cavendish) and put their work in a sound theoretical framework.
In his 1789 treatise on chemistry—regarded by some as the first modern textbook of chemistry—Lavoisier presented a unifying theory that elucidated the concept of a chemical element and how these can form chemical compounds. He pioneered the concepts of stoichiometry and the conservation of mass, and argued strongly against the phlogiston theory. As is sometimes the case in science, a number of the major proponents of the phlogiston theory were unmoved; however, the next generation of chemists found Lavoisier's arguments convincing and the phlogiston theory was abandoned.
The chemistry of the respiratory gases played a central role in Lavoisier's thinking. He recognized that both combustion and breathing involve the consumption of O 2 and production of CO 2 .
Lavoisier defended Lagrange and other foreign-born scientists whose rights were being abridged by the government. During the Reign of Terror, Lavoisier was summarily tried, convicted, and executed on May 8, 1794. For more information about Antoine Lavoisier, visit the following websites:
N26-6
Joseph-Louis Lagrange (1736–1813)
Giuseppe Lodovico Lagrangia—an astronomer and one of the greatest mathematicians of his time—was born in Turin, moved to Berlin in 1766, and then moved to Paris in 1786. He survived the French Revolution and died in France.
Lagrange's contribution to biology—specifically to respiratory physiology—is a conclusion that he based entirely on theory: he concluded that respiration (i.e., combustion) within the body could not take place entirely within the lungs because this would be inconsistent with the even distribution of heat throughout the body.
For more information about Lagrange, consult the following sources:
- 1
- 2
Holmes FL: Lavoisier and the Chemistry of Life. Madison, WI, University of Wisconsin Press, 1985.
N26-7
Lazzaro Spallanzani (1729–1799)
Lazzaro Spallanzani was an ordained Catholic priest and scientist who made contributions in a wide range of biological disciplines, including reproduction, regeneration (e.g., of amphibian limbs), and respiration. He argued strongly against the theory of spontaneous generation. His work on respiration, published posthumously, demonstrated that several tissues consume O 2 and evolve CO 2 .
For more information about Spallanzani, consult the following sources:
- 1
- 2
http://www.accessexcellence.org/RC/AB/BC/Spontaneous_Generation.php .
- 3
- 4
- 5
- 6
Keilin D: The History of Cell Respiration and Cytochrome. Cambridge, UK, Cambridge University Press, 1966.
Thus, by the end of the 18th century, chemists and physiologists appreciated that combustion, putrefaction, and respiration all involve chemical reactions that consume O 2 and produce CO 2 . Subsequent advances in the chemistry of gases by Boyle, Henry, Avogadro, and others laid the theoretical foundation for the physiology of O 2 and CO 2 . Thus, respiration was a unifying theme in the early histories of physiology, chemistry, and biochemistry.
Later work showed that mitochondrial respiration (i.e., the oxidation of carbon-containing compounds to form CO 2 ) is responsible for the O 2 consumption and CO 2 production observed by Spallanzani. This aspect of respiration is often called internal respiration or oxidative phosphorylation (see p. 1185 ).
In the chapters on respiratory physiology, we focus on external respiration, the dual processes of (1) transporting O 2 from the atmosphere to the mitochondria and (2) transporting CO 2 from the mitochondria to the atmosphere. We will also see that CO 2 transport is intimately related to acid-base homeostasis.
Diffusion is the major mechanism of external respiration for small aquatic organisms
The most fundamental mechanism of O 2 and CO 2 transport is diffusion (see p. 108 ). Random movements of molecules such as O 2 and CO 2 , whether in a gaseous phase or dissolved in water, result in a net movement of the substance from regions of high concentration to regions of low concentration ( Fig. 26-1 A , inset). No expenditure of energy is involved. The driving force for diffusion is the concentration gradient.
Imagine a unicellular organism suspended in a beaker of pond water at 37°C. The water is in equilibrium with an atmosphere that has the usual composition of O 2 and CO 2 ( Table 26-1 ). The partial pressures of O 2 ( 
) and of CO 2 ( 
) in the dry air are slightly higher than their corresponding values in the wet air immediately above the surface of the water ( Box 26-1 ). It is these partial pressures in wet air that determine the concentrations of dissolved O 2 ([O 2 ] dis ) and dissolved CO 2 ([CO 2 ] dis ) in the water ( Box 26-2 ). Thus, the 
in the wet air—as well as the water beneath it—will be ~149 mm Hg (or torr), and the will be an almost negligible 0.2 mm Hg. These numbers describe the composition of the bulk phase of the pond water (see Fig. 26-1 A , left side), at some distance from the organism. However, because the mitochondria within the organism continuously consume O 2 and produce CO 2 , the 
at the surface of the mitochondria will be lower than the bulk-phase 
, whereas the at the mitochondrial surface will be higher than the bulk-phase (see Fig. 26-1 A , right side). These differences in partial pressure cause O 2 to diffuse from the bulk pond water toward the mitochondria and the CO 2 to diffuse in the opposite direction.
TABLE 26-1
Composition of Air
| DRY AIR ATMOSPHERE | WET AIR TRACHEA | |||
|---|---|---|---|---|
| GAS | FRACTION IN AIR (%) | PARTIAL PRESSURE AT SEA LEVEL (mm Hg) | FRACTION IN AIR (%) | PARTIAL PRESSURE AT SEA LEVEL (mm Hg) |
| Nitrogen | 78.09 | 593.48 | 73.26 | 556.78 |
| Oxygen | 20.95 | 159.22 | 19.65 | 149.37 |
| Carbon dioxide | 0.03 | 0.23 | 0.03 | 0.21 |
| Argon | 0.93 | 7.07 | 0.87 | 6.63 |
| Water | 0 | 0 | 6.18 | 47 |
| Total | 100 | 760 | 100 | 760 |
Box 26-1
Wet Gases
Imagine that a beaker of water is equilibrated with a normal atmosphere and that both water and atmosphere have a temperature of 37°C. For dry air (i.e., air containing no water vapor), O 2 makes up ~21% of the total gas by volume (see Table 26-1 ). Thus, if the ambient pressure—or barometric pressure (P b ) —is 760 mm Hg, the partial pressure of O 2 ( 
) is 21% of 760 mm Hg, or 159 mm Hg ( Fig. 26-2 ). However, if the air-water interface is reasonably stationary, water vapor will saturate the air immediately adjacent to the liquid. What is the 
in this wet air? At 37°C, the partial pressure of water ( 
) is 47 mm Hg. Of the total pressure of the wet air, 
makes up 47 mm Hg, and the components of the dry air make up the remaining 760 − 47, or 713 mm Hg. Thus, the partial pressure of O 2 in this wet air is
The CO 2 composition of dry air is ~0.03% (see Table 26-1 ). Thus, the partial pressure of CO 2 in wet air is
These examples are realistic for respiratory physiology. As we inhale relatively cool and dry air, the nose and other upper respiratory passages rapidly warm and moisturize the passing air so that it assumes the composition of wet air given in Table 26-1 .
Box 26-2
Partial Pressures and Henry's Law
Respiratory physiologists generally express the concentration of a gas, whether it is mixed with another gas (e.g., O 2 mixed with N 2 , as is the case for air) or dissolved in an aqueous solution (e.g., O 2 dissolved in water), in terms of partial pressure. Dalton's law states that the total pressure (P total ) of a mixture of gases is the sum of their individual partial pressures. Imagine that we are dealing with an ideal gas (Z) mixed with other gases. Because the ratio of the partial pressure of Z (P Z ) to the total pressure (P total ) is its mole fraction (X Z ),
Thus, if P Z in one sample of gas were twice as high as in another, X Z (i.e., concentration of Z) would also be twice as high.
It may not be immediately obvious why—when Z is dissolved in aqueous solutions—it is still reasonable to express the concentration of Z in terms of P Z . According to Henry's law, the concentration of O 2 dissolved in water ([O 2 ] dis ) is proportional to 
in the gas phase:
The proportionality constant s is the solubility; for O 2 , s is ~0.0013 mM/mm Hg at 37°C for a solution mimicking blood plasma. The solubility of CO 2 is ~23-fold higher. Consider a beaker of water at 37°C equilibrated with an atmosphere having a 
of 100 mm Hg, the partial pressure in mammalian arterial blood plasma ( Fig. 26-3 A , solution #1):
Now consider a second beaker equilibrated with an atmosphere having a 
of 40 mm Hg, the partial pressure of O 2 in mixed-venous blood (see Fig. 26-3 A , solution #2):
If we now place samples of these two solutions on opposite sides of a semipermeable barrier in a closed container (see Fig. 26-3 B ), the O 2 gradient across this barrier expressed in terms of concentrations (Δ[O 2 ]) is 0.13 − 0.05 or 0.08 mM. Expressed in terms of partial pressures ( 
), this same gradient is 100 − 40 = 60 mm Hg.
Imagine now that we take a 5-mL sample of each of the solutions in the beakers in Figure 26-3 A , drawing the fluid up into syringes, sealing the syringes, putting them on ice, and sending them to a clinical laboratory for analysis—as is routinely done with samples of arterial blood. Even though there is no gas phase in equilibrium with either of the solutions in the syringes, the laboratory will report the O 2 levels in millimeters of mercury (mm Hg). These are the partial pressures of O 2 with which the solutions were or would have to be equilibrated to achieve the [O 2 ] dis in the liquid samples.
N26-8
Gas Laws
In the mid-17th century, Robert Boyle demonstrated that the relation between the pressure (P) and volume (V) of a real gas at a fixed temperature is essentially hyperbolic. Boyle's law states that P and V for an ideal gas vary inversely:
At the molecular level, the pressure exerted by a fixed number of gas molecules—the total force of gas per unit surface area of the container—reflects the number of collisions molecules make with the walls of the container. If we reduce the container's volume by half, the number of collisions doubles for each square centimeter of the container's walls, and, therefore, pressure doubles.
A century after Boyle's work, Jacques Charles found that the volume of a gas varies linearly with absolute temperature (T, in kelvin) if pressure is constant:
At the molecular level, Charles's law states that increasing the temperature increases the velocity of gas molecules, which forces the perfectly compliant container to increase in size.
Combining these two laws yields the so-called Boyle-Charles law:
For an ideal gas, “constant #3” is nothing more than n · R, where n is the number of moles and R is the universal gas constant. Incorporating n and R into Equation NE 26-3 yields the ideal gas law:
If we compare the relationship among pressure, volume, and temperature for a fixed number of moles of the gas under two conditions, we see that
With this simple equation, one better appreciates what happens when barometric pressure increases during diving or decreases during ascent to high altitude.
The barometric pressure (P b ) is the sum of the partial pressures of the individual gases in the air mixture ( Dalton's law; see Box 26-2 ). Thus, in the case of ordinary dry air (see Table 26-1 ), most of the sea-level P b of 760 mm Hg is due to N 2 (~593 mm Hg) and O 2 (~159 mm Hg), with smaller contributions from trace gases such as argon (~7 mm Hg) and CO 2 (~0.2 mm Hg). Thus, as P b increases during diving beneath the water, or as P b decreases during ascent to high altitude, the partial pressure of each constituent gas will change in proportion to the change in P b . This relationship is important for O 2 delivery to tissues, because a key variable that determines the O 2 saturation of hemoglobin (Hb) is 
in the inspired air (see p. 681 ).
The conducting airways humidify inspired air so that it becomes fully saturated with H 2 O vapor at body temperature (see Box 26-1 ). The H 2 O vapor then occupies part of the space in the lungs. At a body temperature of 37°C, 
is 47 mm Hg. If P b is 760 mm Hg, only 760 − 47 = 713 mm Hg is available for the sum of 
, 
, and 
. Because H 2 O readily evaporates from (or condenses into) liquid water, its partial pressure does not change with changes in P b .
The diffusion of O 2 follows a gradient of decreasing 
(see Fig. 26-1 A ). The region over which 
falls gradually from the bulk pond water toward the outer surface of the plasma membrane is the extracellular unstirred layer, so named because no convective mixing occurs in this zone. A similar gradual decline in 
drives O 2 diffusion through the intracellular unstirred layer, from the inner surface of the plasma membrane to the mitochondria. The abrupt fall in 
across the plasma membrane reflects some resistance to gas flow. The profile for is similar, although with the opposite orientation.
The rate at which O 2 or CO 2 moves across the surface of the organism is the flow ( units: moles/s). According to a simplified version of Fick's law (see p. 108 ), flow is proportional to the concentration difference across this barrier. Because we know from Henry's law that the concentration of a dissolved gas is proportional to its partial pressure in the gas phase, flow is also proportional to the partial-pressure difference (ΔP):
Simple diffusion is the mechanism by which O 2 and CO 2 move short distances in the respiratory system: between the air and blood in the alveoli, and between the mitochondria and blood of the peripheral circulation.
Convection enhances diffusion by producing steeper gradients across the diffusion barrier
A purely diffusive system can establish only a relatively small ΔP across the gas exchange barrier of the organism (see Fig. 26-1 A ). Yet, for small organisms, even this relatively small ΔP is adequate to meet the demands for O 2 uptake and CO 2 removal. However, when the organism's diameter exceeds ~1 mm, simple diffusion becomes inadequate for gas exchange. One way of ameliorating this problem is to introduce a mechanism for convection on the outside surface of the organism. For a paramecium, the beating cilia bring bulk-phase water—having a 
of ~154 mm Hg at 25°C and a of ~0.2 mm Hg—very near to the cell's surface. This mixing reduces the size of the extracellular unstirred layer, thereby increasing the 
and decreasing the on the outer surface of the organism. The net effect is that the partial-pressure gradients for both O 2 and CO 2 increase across the gas exchange barrier (see Fig. 26-1 B ), leading to a proportionate increase in the flow of both substances.
A filter feeder, such as an oyster or a clam, pumps bulk-phase water past its organ of gas exchange. Because of the relatively low solubility of O 2 in water, such an organism may need to pump 16,000 mL of water to extract a mere 1 mL of O 2 gas. In fish, which are far more efficient, the ratio may be considerably lower, ~400 : 1.
In mammals, the bulk phase is the atmosphere and the external convective system is an air pump that includes the chest wall, the respiratory muscles, and the passages through which the air flows (i.e., from the nose up to the alveoli). Ventilation is the process of moving air into and out of the lungs. Amphibians move air into their lungs by swallowing it. Reptiles, birds, and mammals expand their lungs by developing a negative pressure inside the thorax. Because of the much higher O 2 content of air (about 210 mL O 2 /L of air at standard temperature and pressure/dry, or STPD; Box 26-3 ), as opposed to water (~35 mL O 2 /L of water), humans need to move far less air than oysters need to move water. For example, a human may ventilate the alveoli with 4000 mL of fresh air every minute and extract from this air 250 mL of O 2 gas, a ratio of 16 : 1.
Box 26-3
Conventions for Measurement of Volumes of Gases
BTPS
Gases within the lung are saturated with water vapor at 37°C (310 K). At this temperature, 
is 47 mm Hg (see Box 26-1 ). If the glottis is open and no air is flowing, then the total pressure of the air in the lungs is P b , which we will assume to be 760 mm Hg. In this case, the partial pressure of dry gases in the lungs is (760 − 47) = 713 mm Hg. The convention is to report the volume of gases in the lungs—and changes in the volume of these gases—at body temperature and pressure, saturated with water vapor, or BTPS. Such volumes include both wet and dry gases.
ATPS
If a volume of air is exhaled from the lungs (ΔV BTPS ) into a spirometer, the “floor” of which is formed by water (see Fig. 26-8 ), the exhaled air will now be at ambient temperature and pressure, saturated with water vapor, or ATPS. Thus, we must correct the volume change (ΔV ATPS ) registered by the spirometer (at ATPS) to know the volume that this same gas had occupied in the lungs (at BTPS). Two factors are at work as warm alveolar air moves into a cooler spirometer: (1) 
decreases and some gaseous H 2 O condenses into liquid H 2 O, according to the temperature dependence of 
; and (2) the pressure exerted by the dry gas molecules decreases, according to Charles's law. N26-8 If we start from the Boyle-Charles law,
it is possible to show that N26-12
Here, T body and T ambient are absolute temperatures.
If T body is 37°C (310 K), then the corresponding 
is 47 mm Hg. If T ambient is 25°C (or 298 K), then the corresponding 
is 24 mm Hg. For these conditions, the conversion from an ATPS volume to a BTPS volume becomes
Thus, the same wet gas that occupies 1000 mL in the spirometer at ATPS occupies 1074 mL in the lungs at BTPS.
STPD
The convention is to report the volume of gases in the blood (e.g., dissolved CO 2 or O 2 bound to hemoglobin) in the same way that chemists would—at standard temperature and pressure/dry, or STPD. The standard temperature is 0°C (273 K), and the standard pressure is 760 mm Hg. You may recall from introductory chemistry that a mole of an ideal gas occupies 22.4 L at STPD. If you wish to convert a ΔV STPD to a ΔV BTPS , it is possible to show that N26-13
For a body temperature of 37°C, the conversion from a BTPS volume to an STPD volume becomes
Thus, the same dry gas that occupies 1000 mL under standard chemical conditions occupies 1210 mL in the body at BTPS.
N26-12
Conversion from ΔV BTPS to ΔV ATPS
The basis for our derivation will be the ideal gas law:
We are interested in following a portion of the total volume of gas in the lungs as this volume moves from the lungs—at BTPS —to a spirometer in equilibrium with liquid water—at ATPS. In the lungs, the volume exiting is ΔV BTPS . We will focus on the number of gas molecules in the volume ΔV BTPS :
Let us assume that the pressure inside the lungs (P BTPS ) is the same as barometric pressure (P b ), which is true when no air is flowing and the glottis is open:
The n in Equation NE 26-13 has two components: H 2 O and the dry gases (i.e., everything other than H 2 O). The number of dry-gas molecules is proportional to the partial pressure of the dry gases. Thus,
For example, if P b is 760 mm Hg and body temperature is 37°C, then the number of dry molecules is
Now, what volume would these same dry gas molecules occupy after exhalation into a spirometer at ambient temperature (T ATPS )? We will assume that the ambient pressure is P b . Rearranging the ideal gas law, we get
Substituting into Equation NE 26-16 the value for n dry from Equation NE 26-14 yields
Canceling R and rearranging terms, we get
For example, if P b is 760 mm Hg and ambient temperature is 25°C, then the volume occupied by the dry molecules exhaled from the lungs is
In other words, if the dry gas molecules occupied 1 L in the lungs, they would occupy only 902 mL in the spirometer.
However, this volume of dry-gas molecules does not represent all of the gas that we exhaled … we also exhaled water vapor. What volume does the water vapor occupy after we exhale it into the spirometer? The answer to this question may sound a bit strange, but the volume (or number) of water molecules exhaled from the lungs does not determine the volume (or number) of water molecules in the spirometer. The reason is that the partial pressure of H 2 O in the spirometer—the gas phase of which is in equilibrium with liquid H 2 O—depends not on the amount of H 2 O vapor that is exhaled but only on ambient temperature. Consider four examples:
If body temperature is higher than ambient temperature (i.e., 
is higher in the body than in the spirometer), then some of the exhaled H 2 O molecules condense into the liquid of the spirometer. This is the usual case. Once in the spirometer, the dry-gas molecules from the lungs are accompanied by fewer gaseous H 2 O molecules than had accompanied them in the lungs!
If the body temperature were the same as ambient temperature, then the number of H 2 O molecules that accompanied the exhaled dry gas in the lungs would be the same as the number of H 2 O molecules that accompany this exhaled dry gas in the spirometer. In other words, ΔV BTPS would be the same as ΔV ATPS .
If the body temperature were lower than ambient temperature, then the exhaled H 2 O molecules would be joined in the gas phase of the spirometer by additional H 2 O molecules evaporating from the spirometer's liquid water. In other words, once in the spirometer, the dry-gas molecules from the lungs would be accompanied by more gaseous H 2 O molecules than they had been accompanied by in the lungs!
Finally, imagine that, instead of exhaling into the spirometer a volume ΔV of BTPS air—consisting of both dry air and H 2 O vapor—we instead introduce into the spirometer only the dry air at body temperature contained within ΔV BTPS . This dry air will be joined in the gas phase of the spirometer by H 2 O molecules that evaporate from the spirometer's liquid water … and the final ΔV in the spirometer will be the same as if we had exhaled BTPS (i.e., wet) air into the spirometer!
Thus, in computing the total change in spirometer volume (ΔV ATPS ) we do not need to consider the number of H 2 O molecules exhaled from the lungs; we only need to compute how many gaseous H 2 O molecules must accompany the exhaled dry-gas molecules once these dry-gas molecules are in the friendly confines of the spirometer. We will approach this problem by computing the ratio of dry to total gas molecules contained in ΔV ATPS . Within the volume ΔV ATPS —inside the spirometer—the ratio of number of gas molecules is the same as the ratio of their respective pressures:
Because total pressure is P b , and because the partial pressure of the dry gases is the difference between P b and the vapor pressure of H 2 O,
Because the volume occupied by the gases is proportional to the number of gas molecules,
Solving for the total ΔV ATPS , we get
Equation NE 26-23 tells us that, if we know the volume that the exhaled dry gases occupy once they are in the spirometer, we can easily compute the total volume occupied by these dry molecules and their obligated H 2 O molecules. Substituting into Equation NE 26-23 our expression for ΔV of the dry molecules at ATPS in Equation NE 26-18 , we get
Thus, if P b is 760 mm Hg and ambient temperature is 25°C, then
If we wish to convert back from ΔV ATPS to ΔV BTPS , then the comparable equations are
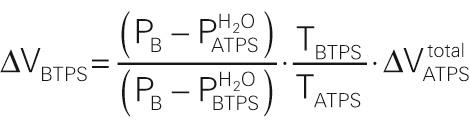
Equation NE 26-28 is the same as the last equation under the heading “ATPS” in Box 26-3 .
N26-13
Conversion from ΔV BTPS to ΔV STPD
The basis for our derivation will be the ideal gas law:
We are interested in following a portion of the total volume of gas in the lungs as this volume moves from the lungs—at BTPS —to a spirometer in equilibrium with liquid water—at ATPS. In the lungs, the volume exiting is ΔV BTPS . We will focus on the number of gas molecules in the volume ΔV BTPS :
Let us assume that the pressure inside the lungs (P BTPS ) is the same as barometric pressure (P b ), which is true when no air is flowing and the glottis is open:
The n in Equation NE 26-31 has two components: H 2 O and the dry gases (i.e., everything other than H 2 O). The number of dry-gas molecules is proportional to the partial pressure of the dry gases. Thus,
For example, if P b is 760 mm Hg and body temperature is 37°C, then the number of dry molecules is
Up to this point, the discussion has been identical to that in N26-12 , where we asked what volume this dry gas (as well as its obligated water vapor) would occupy at ATPS. In this webnote, we instead ask what volume these exhaled dry gas molecules would occupy at standard temperature and standard pressure. The definitions are the following:
Rearranging the ideal gas law, we get
Substituting into Equation NE 26-36 the value for n dry from Equation NE 26-32 yields
Canceling R and rearranging terms, we get
For example, if P b is 760 mm Hg, then the volume occupied by the dry molecules exhaled from the lungs is
In other words, if the dry gas molecules occupied 1 L in the lungs, they would occupy only 826 mL in the spirometer.
If we wish to convert back from ΔV STPD to ΔV BTPS , then the comparable equations are
Equation NE 26-41 is the same as the last equation under the heading “STPD” in Box 26-3 .
Although we are 1000-fold more efficient than oysters, the principle of external convective systems is the same: ensure that the external surface of the gas exchange barrier is in close contact with a fluid whose composition matches—as closely as is practical—that of the bulk phase. How “closely” is “practical”? The composition of alveolar air approaches that of wet inspired air as alveolar ventilation approaches infinity (see p. 680 ). Because high ventilatory rates have a significant metabolic cost, the body must trade off optimizing alveolar 
and on the one hand against minimizing the work of ventilation on the other. In the average adult human, the compromise that has evolved is an alveolar ventilation of ~4000 mL/min, an alveolar 
of ~100 mm Hg (versus 149 mm Hg in a wet atmosphere at 37°C), and an alveolar of ~40 mm Hg (versus 0.2 mm Hg).
A clinical example in which the external convective system fails is barbiturate poisoning. Here, drug intoxication inhibits the respiratory control centers in the medulla (see p. 700 ), so that ventilation slows or even stops. The consequence is that the unstirred layer between the bulk-phase atmosphere and the alveolar blood-gas barrier becomes extremely large (i.e., the distance between the nose and the alveoli). As a result, alveolar 
falls to such low levels that the 
across the alveolar wall cannot support an O 2 flow and an arterial [O 2 ] that is compatible with life. Cessation of ventilation also causes the alveolar to rise to such high levels that the CO 2 flow from blood to alveolar air is unacceptably low.
An external convective system maximizes gas exchange by continuously supplying bulk-phase water or air to the external surface of the gas exchange barrier, thereby maintaining a high external 
and a low external . A circulatory system is an internal convective system that maximizes flow of O 2 and CO 2 across the gas exchange barrier by delivering, to the inner surface of this barrier, blood that has as low a 
and as high a as is practical. Perfusion is the process of delivering blood to the lungs. Figure 26-1 C shows a primitive—and hypothetical—internal convective system, one that essentially stirs the entire internal contents of the organism, so that the 
of the bulk internal fluids is uniform, right up to the surface of the mitochondria. The result is that the 
across the gas exchange barrier is rather large, but the 
between the bulk internal fluid and the mitochondria is rather small.
Figure 26-1 D summarizes the 
and profiles for a sophisticated circulatory system built around a four-chambered heart and separate pulmonary and systemic circulations. The circulatory system carries (by convection) low- 
blood from a systemic capillary near the mitochondria to the alveolar wall. At the beginning of a pulmonary capillary, a high alveolar-to-blood 
gradient ensures a high O 2 inflow (by diffusion), and blood 
rises to match the alveolar (i.e., external) 
by the time the blood leaves the pulmonary capillary. Finally, the systemic arterial blood carries (by convection) this high- 
blood to the systemic capillaries, where a high blood-to-mitochondria 
gradient maximizes the O 2 flux into the mitochondria (by diffusion). The opposite happens with CO 2 . Thus, separate pulmonary and systemic circulations ensure maximal gradients for gas diffusion in both the pulmonary and systemic capillaries.
The scenario outlined in Figure 26-1 D requires the four-chambered heart characteristic of mammals as well as of advanced reptiles and birds. The right ventricle pumps low- 
/high- blood received from the peripheral veins to the lungs, whereas the left ventricle pumps high- 
/low- blood received from pulmonary veins to the periphery (i.e., mitochondria). Maintenance of maximal gradients for O 2 and CO 2 diffusion in both the pulmonary and systemic capillaries at the mitochondria requires that right and left ventricular blood not mix. However, this sort of mixing is exactly what occurs in fish and amphibians, whose hearts have a common ventricle. In these animals, the aortic blood has 
and values that are intermediate between the extreme values of venous blood returning from the systemic circulation and the blood returning from the gas exchange barrier. The result is less than optimal 
and gradients at both the gas exchange barrier and the mitochondria.
In humans, the internal convective system may fail when diseased heart valves cause a decrease in cardiac output. Another example is the shunting of blood between the pulmonary and the systemic circulations, as may occur in newborns with congenital anomalies (e.g., atrial or ventricular septal defects). The result is the same sort of mixing of systemic venous and gas exchange barrier blood that occurs in amphibians and fish. Thus, patients with shunts cannot establish normal 
and gradients in the pulmonary and peripheral capillaries and thus cannot generate normal flows of O 2 and CO 2 .
Surface area amplification enhances diffusion
The passive flow of O 2 or CO 2 across a barrier is proportional not only to the concentration gradient but also to the area of the barrier: N26-9
N26-9
Flow Versus Flux
On page 595 of the text, we state that the flow of a gas across the blood-gas barrier is proportional to (1) the driving force—in this case the partial-pressure gradient (ΔP) of the gas—across the barrier, and (2) the area of the barrier. This concept is embodied in Equation 26-2 (shown here as Equation NE 26-6 ):
Note that flow has the units of mass per unit time, such as mL/s. The flow per unit area is known as the flux, which might have the units of mL/(cm 2 s). Thus, the area term does not appear in the equation that describes flux:
Equation NE 26-7 is a restatement of Fick's law, which we introduced in the text in Equation 5-13 and also Equation 20-4 . For a more detailed discussion of Fick's law see N20-2 .
In the case of the lung, pulmonary specialists do not work with flux values, but with flow values because the surface area over which diffusion occurs is generally not known.
Indeed, higher animals have increased their ability to exchange O 2 and CO 2 with their environment by increasing the surface area across which gas exchange takes place. For example, mollusks (e.g., squid) and fish have gills, which they form by evaginating the gas exchange barrier, thus greatly amplifying its surface area. Higher land animals amplify their gas exchange barriers by invaginating them, forming lungs. In an amphibian such as the adult frog, the lungs are simple air sacs with a relatively small surface area. Not surprisingly, a large portion of their gas exchange must occur across the skin. The gas exchange barrier is considerably more sophisticated in reptiles, which line their lungs with alveoli or even subdivide them with alveoli-lined barriers. The net effect is to increase the surface-to-volume ratio of the lungs. Mammals increase the area available for diffusion even more, by developing highly complex lungs with bronchi and a large number of alveoli.
In humans, the lung surface is so large and so thin that O 2 and CO 2 transport across the alveolar wall is ~3-fold faster than necessary—at least when the person is resting at sea level. Nevertheless, this redundancy is extremely important during exercise (when cardiac output can increase markedly), for life at high altitude (where the 
is low), and in old age (when lung function diminishes). A substantial decrease in surface area, or thickening of the barrier, can be deleterious. Examples are the surgical removal of a lung (which reduces the total surface for gas exchange by about half) and pulmonary edema (which increases the effective thickness of the barrier). Thus, if an individual with a thickened barrier loses a lung, the remaining surface area may not be large enough to sustain adequate rates of gas exchange.
Respiratory pigments such as hemoglobin increase the carrying capacity of the blood for both O 2 and CO 2
In mammals, the external convective system (i.e., ventilatory apparatus), the internal convective system (i.e., circulatory system), and the barrier itself (i.e., alveolar wall) are so efficient that the diffusion of O 2 and CO 2 is not what limits the exchange of gases, at least not in healthy subjects at sea level.
Imagine what would happen if the mixed-venous blood flowing down a pulmonary capillary contained only water and salts. The diffusion of O 2 from the alveolar air space into the “blood” is so fast—and the solubility of O 2 in saline is so low (see Box 26-2 )—that before the blood could move ~1% of the way down the capillary, the 
of the blood would match the 
of the alveolar air (i.e., all of the O 2 that could move would have moved). For the remaining ~99% of the capillary, the 
gradient across the barrier would be nil, and no more O 2 would flow into the blood. As a result, at a normal cardiac output, the blood could never carry away enough O 2 from the lungs to the tissues to sustain life. The same would be true in reverse for the elimination of CO 2 .
Animals solve this problem with respiratory pigments, specialized metalloproteins that—via the metal—reversibly bind O 2 , greatly increasing the carrying capacity of blood for O 2 . In some arthropods and mollusks, the pigment is hemocyanin, which coordinates two copper atoms. Polychaete worms and brachiopods use hemerythrins, which coordinate two iron atoms. However, the most common—and most efficient—respiratory pigments are the hemoglobins, which coordinate a porphyrin ring that contains iron. All vertebrates as well as numerous unrelated groups of animals use hemoglobin, which is the chief component of erythrocytes or red blood cells.
The presence of hemoglobin markedly improves the dynamics of O 2 uptake by blood passing through the lungs. Under normal conditions, hemoglobin reversibly binds ~96% of the O 2 that diffuses from the alveolar air spaces to the pulmonary-capillary blood, greatly increasing the carrying capacity of blood for O 2 . Hemoglobin also plays a key role in the transport or carriage of CO 2 by reversibly binding CO 2 and by acting as a powerful pH buffer. In anemia, the hemoglobin content of blood is reduced, thus lowering the carrying capacity of blood for O 2 and CO 2 . An individual with anemia can compensate only if the systemic tissues extract more O 2 from each liter of blood or if cardiac output increases. However, there are limits to the amount of O 2 that tissues can extract or to the level to which the heart can increase its output.
You're Reading a Preview
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here