Does Strain in the Patella Change After Total Knee Arthroplasty? A Finite Element Investigation of Natural and Implanted Patellae

Materials and Methods

Specimen-specific FE models for eight male subjects were developed from CT and magnetic resonance imaging (MRI) scans of cadaveric knees. Femoral, tibial, and patellar bone and cartilage were reconstructed from MRI data, and patellar bone geometry was extracted from CT data. Eight-noded hexahedral meshes of articular cartilage were semiautomatically generated from the segmented geometries using custom-scripted coordinate data extraction and mesh morphing techniques. A convergence study was performed to determine an appropriate element size for the patellar bone mesh. Tetrahedral meshes with element edge length of 1.25, 1, and 0.8 mm were compared. Differences in average strain (per unit volume) between the coarsest and finest mesh were less than 0.03% in natural and implanted models. Perillo-Marcone et al. reported an element size comparable with the slice thickness of CT images to be sufficient for mesh convergence; they recommended an element size of 1.4 mm for convergence of the Young modulus, along with stress and risk results with a CT slice thickness of 1 mm. CT slice thickness for specimens in the current study varied from 0.5 to 1 mm. Based on slice thickness, computational efficiency, and minimal differences between 1 mm and finest mesh, an average element edge length of 1 mm was determined to appropriately represent the heterogeneity captured by CT data. Patellar bones were meshed using four-noded tetrahedral elements, such that natural and implanted patellae shared an element subset ( Fig. 22.1A ). The shared anterior element set ensured that muscle load could be applied through a common extensor mechanism in both models, eliminating potential differences in load application. Average numbers of elements in natural and implanted patellae were 140,000 and 85,000, respectively.

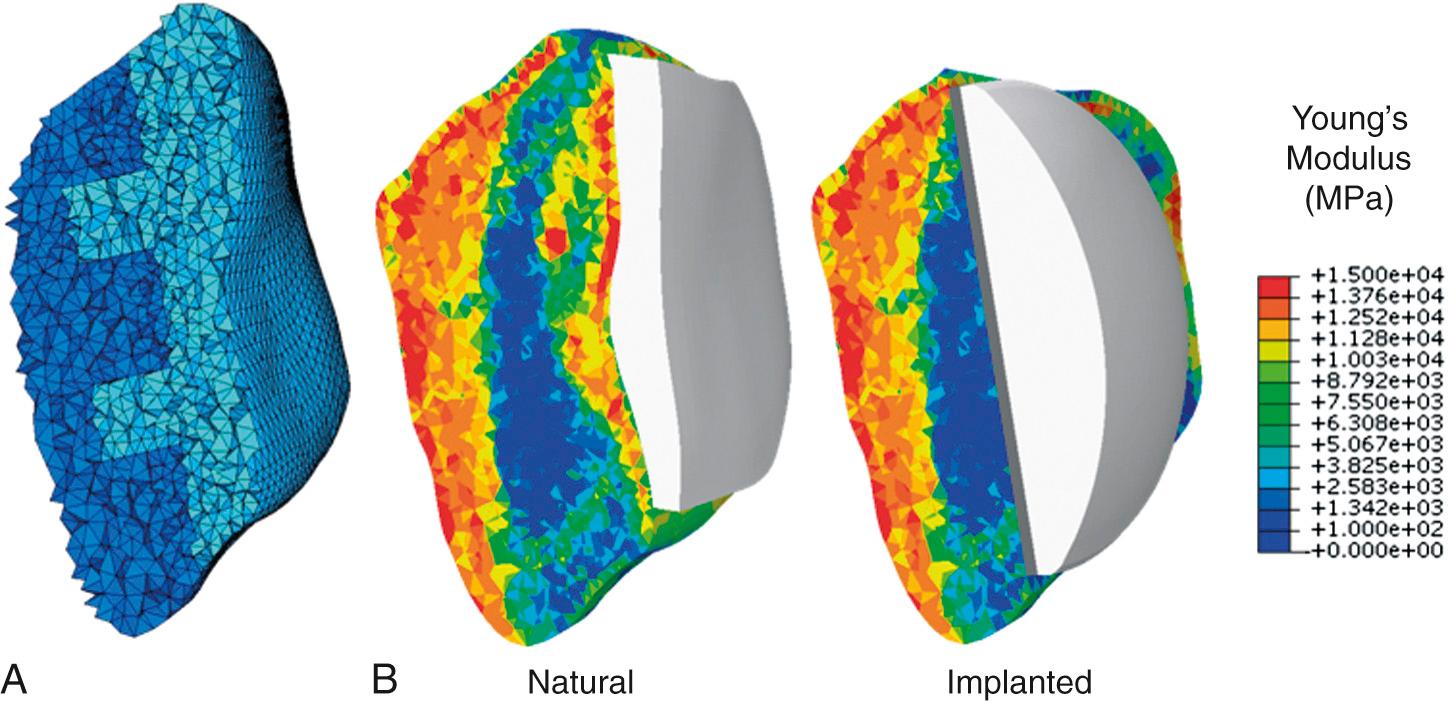
Two model representations were developed for each specimen: a natural model with bone and cartilage and an implanted model with a size-matched domed patellar button, a femoral component, and a tibial insert. Articular cartilage ( E = 12 MPa, ν = 0.45) and the patellar component ( E = 572 MPa, ν = 0.45) were modeled as fully deformable. In the natural model, patellar cartilage nodes were equivalenced with the posterior patellar bone to facilitate load transfer to the bone. In the implanted model, TKR components were positioned under the guidance of an orthopedic surgeon, and an intermediate cement layer ( E = 3400 MPa, ν = 0.3) was modeled between the patellar bone and button. Nodes were equivalenced between the button and the cement and between the cement and the resected patellar bone surface. For computational efficiency, femoral and tibial bones, in addition to femoral and tibial components, were modeled as rigid bodies using triangular surface elements.

Patellar strain is dependent not only on geometry and loading and contact mechanics but also on material properties of the bone. To account for specimen-specific bone material properties, mapped material properties of the patellar bone were extracted from CT data using BoneMat (Biomed Town, Bologna, Italy) (see Fig. 22.1B ). Calibration of CT data to correlate Hounsfield units (HUs) with apparent density ( ρ ) was performed using a linear relationship taken from the literature. Several studies have derived empirical relationships between bone density and mechanical properties. The power law for the Young modulus, E = 1990 ρ ³ . ⁴⁶ As proposed by Keller was applied in this analysis. The nonlinear nature of the density-elasticity relationship ensures that different properties will be obtained depending on whether the Young modulus for the element is calculated before or after averaging over the element. In a comparative study with experimentally obtained data, Taddei et al. reported that transforming HU values into Young's modulus values prior to averaging over the element was found to improve strain prediction accuracy compared with prior algorithms, which averaged HU values and then transformed them to modulus values. Hence this material mapping algorithm was adopted for the current study and was applied using BoneMat (version 3).

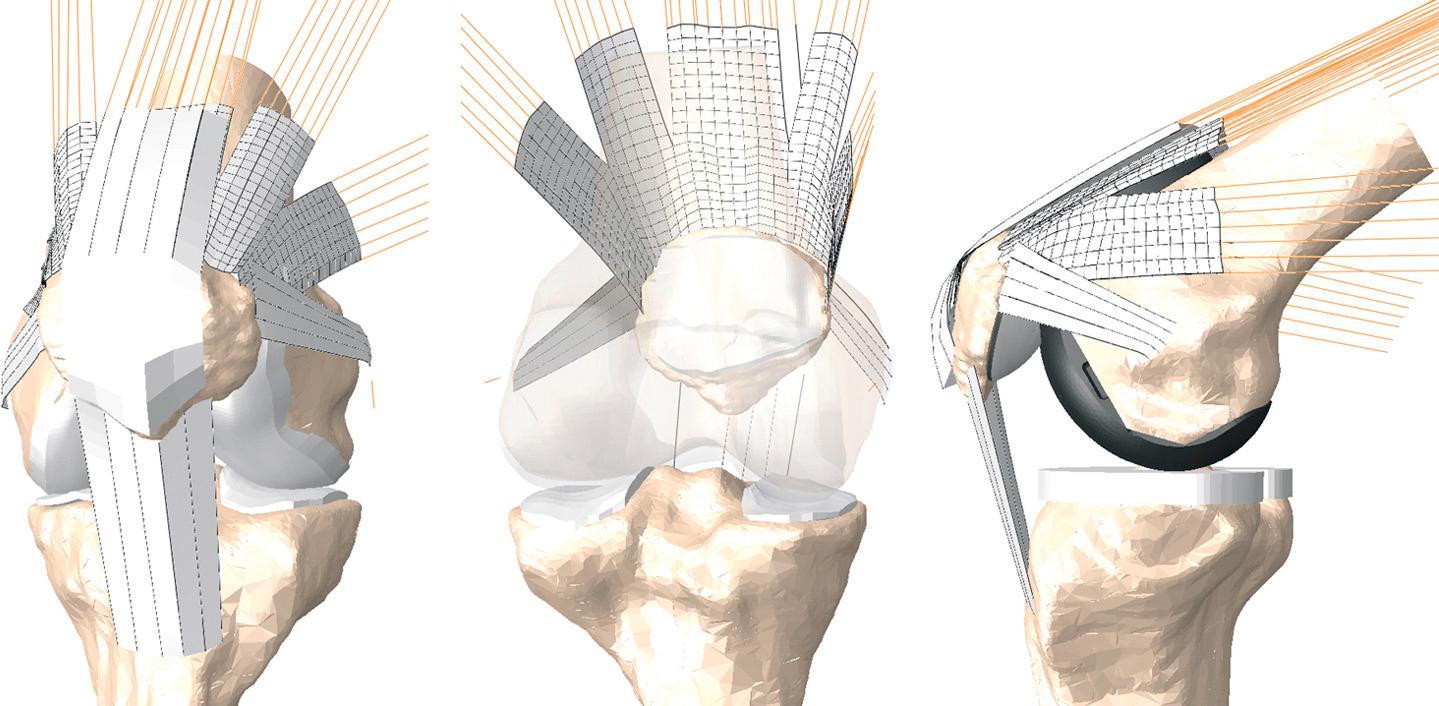
Each natural and implanted model was incorporated into an FE model of the isolated PF joint, which included two-dimensional (2D) fiber-reinforced membrane representations of the extensor mechanism and PF ligaments ( Fig. 22.2 ). An attachment site for each of the patellar ligament vasti, the rectus femoris, and the medial and lateral PF ligaments was defined on the surface of the patellar bone. Each node in the attachment site was rigidly beamed to its closest ligament fiber to physiologically transmit the ligament or muscle load to the patellar bone. A 1000 N ramped load was distributed among the heads of the quadriceps muscle as follows: vastus intermedius, 20%; vastus lateralis longus, 30%; vastus medialis longus, 15%; vasti lateralis obliquus, 10%; vasti medialis obliquus, 10%; and rectus femoris, 15%; these values are proportional to their physiologic cross-sectional areas as measured experimentally by Farahmand et al. Prior to flexion a 300-N load was applied to the quadriceps and was held constant to bring the PF articular surfaces into contact. The quadriceps load was then linearly ramped to 1000 N over a 120-degree simulated deep knee bend.

Maximum and minimum principal strains in the patella were quantified throughout the flexion cycle. Strain distributions throughout the bone volume were compared between natural and implanted conditions. Because peak maximum or minimum strain may occur in a very small localized region and may not provide an appropriate comparison, evaluations of a highly strained volume were performed, representing the bone volume experiencing strain above a specific threshold level. A threshold strain level of 0.5% was selected for comparison between natural and implanted cases. Bayraktar et al. and Kopperdahl and Keaveny, after measuring principal strains in trabecular and cortical bone, reported yield strains in the region of 0.6% to 1%. In addition, patellar bone volume was divided into four discrete regions: superior, medial, lateral, and inferior, centered at the midpoint of the patellar component. Strains in elements adjacent to the pegs of the patellar button were also compared with corresponding elements in the natural case. Strain levels and highly strained volumes in these regions were compared between implanted and natural cases. Finally, relationships between strain and the physical dimensions of the patella were investigated to determine whether strain correlated with size measurements that could be extracted preoperatively from x-rays.