Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
Carrie Haverty provided helpful comments on the manuscript.
The primary challenge of cell-free DNA (“cfDNA”) based prenatal testing (commonly called noninvasive prenatal testing or NIPT) is to identify fetal chromosomal anomalies from maternal plasma samples, where maternal cfDNA molecules far outnumber their fetal counterparts. Further complicating this task is the fact that the relative amounts of fetal and maternal fragments (i.e.; the fetal fraction) varies across pregnancies and gestational ages, reaching as high as 40% and as low as 1%. Therefore, to achieve maximal sensitivity and specificity, a cfDNA test’s analysis pipeline must determine both the fetal fraction (“FF”) of a sample and the likelihood of an aneuploid fetus. Several elegant molecular and bioinformatic strategies have emerged to infer FF and ploidy status reliably and at low cost, yielding a range of cfDNA test offerings that hold in common a remarkably high clinical sensitivity that has driven the rapid adoption of this screening modality. In this chapter, the analysis fundamentals are described for three cfDNA test platforms: whole-genome sequencing (WGS), single-nucleotide polymorphism (SNP), and microarray. The methodologies of aneuploidy identification, FF inference, and microdeletion detection are discussed in turn. These topics provide a basic understanding of how cell-free DNA based prenatal testing works in routine pregnancies and lay the groundwork for a discussion at the end of the chapter about edge cases that will themselves become common as use of the screening grows.
To help guide understanding of the algorithm underlying whole-genome sequencing (WGS)-based NIPT analysis , it is useful first to consider the ultimate goal of NIPT: robust identification of fetal copy-number anomalies in large genomic regions at low FF. The “copy-number anomalies” include trisomies and monosomies in the fetus; “large genomic regions” include whole chromosomes and relatively smaller variants like microdeletions, and we stipulate “low FF” because if the test is sensitive at low FF, then it will surely work well at high FF. This goal provides a framework to evaluate the challenges the analysis algorithm must overcome. For instance, in a pregnancy with 2% FF in which the fetus has trisomy 21—chr21 comprises 1.7% of the genome—only 1 in 3000 cfDNA fragments actually derives from the fetal copies of chr21 (1.7% ⁎ 2%) − 1 . Therefore to detect a 50% increase in the number of fetal copies of chr21 (i.e., from disomic to trisomic) with high statistical confidence, it is not sufficient to sequence thousands or even hundreds of thousands of random cfDNA fragments. Indeed, millions of sequenced cfDNA fragments are required.
The first step of the WGS analysis pipeline is to align the millions of sequenced cfDNA fragments (“reads”) to the human reference genome. Off-the-shelf software packages can map millions of reads to the 3-billion-base human reference genome in the order of minutes . Considering the goal of detecting a low-FF T21 sample, the key question is whether the number of reads mapping to chr21 is higher than expected. A naive approach would be to compare the level of chr21 reads to the reads mapped to a known disomic chromosome: for example, assume that there are two fetal copies of chr1 and use the number of reads mapped to chr1 as an estimate for the number of mapped reads to a disomic chr21 ( Fig. 1 A ). However, for an ordinary euploid sample, chr1 may have 1,000,000 reads while chr21 may have only 200,000, illustrating the folly of comparing read totals across chromosomes: chr1 trivially has ~ 10 × more than chr21 because it is ~ 10 × longer. Instead, for the comparisons of cfDNA abundance that underlie WGS-based analyses, it is best to use a length-agnostic measurement, such as the density of reads ( Fig. 1 B).
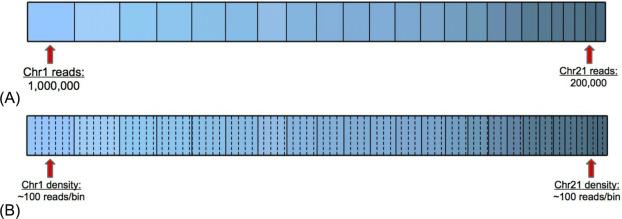
Read density in WGS-based NIPT algorithms is typically assessed by tiling each chromosome with nonoverlapping bins of equal size, counting the number of reads per bin, and averaging the reads per bin over a region of interest (e.g., a microdeletion or whole chromosome) . This process of averaging over bins requires two important choices when implementing the algorithm: the bin size to use and the method for calculating an average.
There is no strictly optimal bin size, yet noteworthy factors inform the choice. One key factor in bin size choice is the total number of reads the sample receives, which was asserted above to be in the tens of millions. In general, total reads and bin size are inversely proportional, with deeper sequencing permitting smaller bins. Ideally, bins should be small enough to allow clear differentiation of aneuploidy-scale deviations in signal from large, spurious deviations that should be omitted from the dataset (e.g., biological events like maternal CNVs or analytical artifacts like alignment mistakes; Fig. 2 ). For instance, if bins are so small that the average bin count is only two reads, the discreteness of NGS reads means that it is not straightforward to interpret a bin with four reads as being from a normal, aneuploid, or maternal-CNV-harboring chromosome. However, with larger bins that have 50 reads on average, it is much simpler to distinguish a deflection consistent with aneuploidy (e.g., 55 reads) from a maternal-CNV-caused deviation (e.g., 100 reads).

While the discretization of individual reads described previously provides an upward pressure on bin size, the existence of localized, anomalous genomic regions exerts a downward pressure that supports the use of smaller bins. These anomalous regions could be bins or portions of bins that have stochastic, idiosyncratic, and/or highly skewed levels of mapped reads; even very high-quality samples contain such regions. Fortunately, such regions are rare across the entire genome, yet they deviate greatly from one of the key underlying assumption of WGS, that is, that cfDNA fragments are uniformly sampled. In practice, the few anomalous bins are discarded from the analysis, demonstrating one reason why a large number of relatively small bins are beneficial. To see another reason, consider a 5-kb segment that is anomalous and rightfully caused its encompassing bin to be discarded. If bins were 20 kb, only 15 kb worth of nonanomalous signal would effectively be lost due to the anomaly. However, if bins were 100 kb, then 95 kb of valid sequence would be lost, illustrating the potentially substantial loss of signal resulting from using large bins. To see this argument from another perspective, suppose small anomalous regions occur every ~ 100 kb. If bin size were set to 200 kb, then nearly every bin would harbor signal-compromising anomalies that jeopardize the ability to accurately identify aneuploidy.
Consistent with the two arguments previously—which exert upward and downward forces on bin size—most WGS-based NIPT algorithms described in the literature use 50 kb bins.
Though it sounds straightforward to calculate an average of reads per bin across the many bins that tile a genomic region of interest, a lot of algorithmic nuance is required to maximize the screen's sensitivity and specificity given a sample's sequenced cfDNA fragments. To appreciate the performance gains from special algorithmic care, recall that WGS-based NIPT is a sampling problem: the sequenced reads in each bin are simply a sampling of the fragments present in the maternal plasma, which are themselves only samples from apoptotic cells in the placenta and other parts of the body. As in any sampling problem (e.g., polling prospective voters before an election), in WGS-based NIPT there is a margin of error by which the observed average reads per bin differ from its underlying and typically unobservable true value. Note that if the error in the calculated average reads per bin is too large, it causes false ploidy calls, thereby undercutting the goal of NIPT. The error can be represented as the standard error, σ /sqrt( N ), where σ is the standard deviation of reads per bin, and N is the number of bins. As N is an immutable property of a chromosome and the selected bin size, it is the standard deviation of reads per bin ( σ ) that drives the error of the observed bin count average. The aim, then, of a well-crafted WGS-based NIPT algorithm is to remove sources of bias that inflate σ such that it can descend to its theoretical minimum (which, by Poisson statistics, is σ ~ sqrt(reads per bin)) .
There are multiple sources of bias in WGS data, but methods exist to remove them or mitigate their effects. As described later, some biases (e.g., GC bias, nonunique sequence, etc.) have known molecular underpinnings and can be corrected with approaches tailored to their origin, while other biases may not have a known source but can be diminished through general robust analysis methods.
Sample-to-sample differences in the propensity with which fragments of particular GC content get sequenced can inflate σ above its theoretical minimum . This so-called GC bias arises due to the different thermodynamics of G:C base pairs, which have three hydrogen bonds, and A:T base pairs, which have two. GC bias can be introduced at any level of the NIPT workflow, including DNA extraction, NGS library preparation, and sequencing itself. To appreciate the manifestation of GC bias in WGS data, recall that the expectation is for WGS to yield a uniform sampling of reads across the genome. However, the empirical distribution of reads is not strictly uniform and instead correlates in part with GC content: cfDNA fragments that have high (~ 80%) or low (~ 20%) GC content often generate fewer reads than expected relative to fragments with average GC content (40%–60%). To correct for GC bias, the algorithm should first assess the extent of bias on a sample-specific basis by calculating the ratio between the observed number of reads with a given GC content and the number of such fragments in the whole genome ( Fig. 3 ). Next, observed fragments can be scaled by their particular GC content and known GC bias: for example, if fragments with 20% GC content were observed to be sequenced with only 50% relative efficiency, then each read observed from a fragment with 20% GC content should be scaled by 1/0.5 = 2.
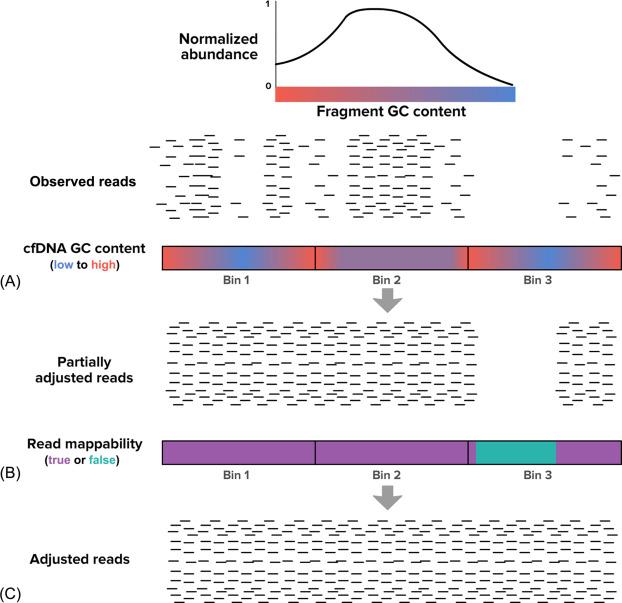
Redundant regions of the genome can also cause nonuniformity in WGS coverage and reduce NIPT accuracy if unaddressed . In redundant regions, it is impossible for the NGS read alignment software to infer the true genomic origin of a fragment. As such, even if a region occurs thousands of times in the genome (e.g., Alu repeats), the aligner may pile reads derived from all of those regions into just a single region; this skewed parsing of reads could create a single bin with a tremendously high number of reads, and many other bins with depressed read values. One way to address degenerate read mappability is to flag redundant regions in advance, mask them altogether to prohibit mapped reads from counting toward the bin total, and then scale the observed reads in a region by the reciprocal of its share of mappable bases (e.g., a bin with 60 reads that is 75% mappable would be scaled to have 80 reads) ( Fig. 3 ).
Maternal copy-number variants (“CNVs”) are another source of potential bias in WGS NIPT data , and their clear biological origin enables specific handling during analysis. In particular, maternal CNVs have a deflection in reads per bin that is very large but also predictable, 50% more or less than the disomic baseline. If such a deflection were of fetal origin, it would be consistent with 100% FF, which is clearly impossible. Maternal CNVs’ predictable signal makes it possible to computationally scan across the genome and identify contiguous spans of bins where the bin counts are increased or decreased by 50%. These bins can then be omitted from the calculation of the region average. Some of the early WGS-based NIPT algorithms did not attempt to identify maternal CNVs, meaning their constituent bins were not omitted from subsequent analysis. These strongly skewed bins increased the mean bin value on CNV-harboring chromosomes to the point that false-positive aneuploidy calls were yielded in several cases. These false-positive results revealed not only a shortcoming in maternal CNV handling, but also a suboptimal, nonrobust method of calculating the average (i.e., the mean), described further later.
Even if a source of bias has unknown molecular origin, its impact can be mitigated if the bias is systematic. For instance, if a bin has elevated reads relative to other bins reproducibly across all samples and with no obvious explanation, it can nevertheless be included in the analysis after a normalization step: for example, by removing signal from the first several principal components or, more simply, by calculating the median number of reads for the bin across a large sample cohort (where the median sample can be assumed to be disomic) and then subtracting this average from the bin in all samples. Applying this normalization procedure across all bins—whether or not they are outliers—reduces the systematic variance in the data and ultimately serves to reduce σ .
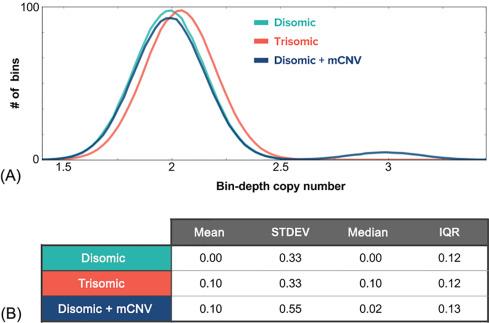
Finally, because any outlying bins that were not filtered out using the previous strategies could yield false results, it is important to reject such bins and/or use robust measures for both the average and the dispersion of bin density ( Fig. 4 ). In particular, for the average, it is best to use the median rather than the mean, as the median will not be skewed by a strong outlier, caused by biological phenomena (e.g., a maternal CNV) or analytical artifacts (e.g., alignment mistakes). For the dispersion, it is best to avoid the standard deviation, as it is susceptible to outliers; the interquartile range (IQR) is a more robust estimator of dispersion. To see the power of using the median and IQR relative to the mean and standard deviation, consider an analysis pipeline that was unaware of the existence of maternal CNVs (mCNVs). With the mean and standard deviation, an mCNV spanning ~ 2% of a chromosome would be enough to strongly risk a false-positive result, whereas using the median and IQR does not risk a false positive until an mCNV spans ~ 30% of the chromosome.
Taken together, the processes of aligning reads to bins, correcting for GC bias and mappability, filtering outlier bins, and averaging in a robust manner yield an observed read density for a region of interest ( μ obs ), but deducing an aneuploidy call from μ obs requires a couple other pieces of information. In particular, to say whether μ obs is statistically higher than expected, it is critical to know both the expected density under a disomic hypothesis ( μ exp ) and the average deviation between μ obs and μ exp , such that assessment of a statistically significant difference is possible.
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here