Physical Address
304 North Cardinal St.
Dorchester Center, MA 02124
In the most general sense, radiation biology is the study of the effects of electromagnetic radiation on biological systems. Three aspects of this definition deserve special mention. First, effects may include everything from DNA damage to genetic mutations, chromosome aberrations, cell killing, disturbances in cell cycle transit and cell proliferation, neoplastic transformation, early and late effects in normal tissues, teratogenesis, cataractogenesis, and carcinogenesis, to name but a few. Electromagnetic radiation refers to any type of radiant energy in motion with wave and/or particulate characteristics that has the capacity to impart some or all of its energy to the medium through which it passes. The amount of energy deposited can vary over some 25 orders of magnitude, depending on the type of electromagnetic radiation. For example, 1 kHz radio waves have energies in the range of 10 –11 to 10 –12 eV, whereas x-rays or γ-rays may have energies upwards of 10 MeV or more. The more energetic forms of electromagnetic radiation, the ionizing radiations, deposit energy as they traverse the medium by setting secondary particles in motion that can go on to produce further ionizations. Finally, biological systems may be, for example, quite simple cell-free extracts of biomolecules, or increasingly complex, from prokaryotes to single-celled eukaryotes, to mammalian cells in culture, to tissues and tumors in laboratory animals or humans, to entire ecosystems.
Radiotherapy-oriented radiobiology focuses on that portion of the electromagnetic spectrum energetic enough to cause ionization of atoms. This ultimately results in the breaking of chemical bonds, which can lead to damage to important biomolecules. The most significant effect of ionizing radiation in this context is cell killing, which directly or indirectly is at the root of nearly all of the normal tissue and tumor responses noted in patients.
Cytotoxicity is not the only significant biological effect caused by radiation exposure, although it will be the main focus of this chapter. Other important radiation effects—carcinogenesis, for example—will also be discussed, although the reader should be aware that radiation carcinogenesis is a large discipline in and of itself, involving investigators from fields as diverse as biochemistry, toxicology, epidemiology, environmental sciences, molecular biology, tumor biology, health and medical physics, as well as radiobiology. Most radiation protection standards are based on minimizing the risks associated with mutagenic and carcinogenic events. Therefore radiological health professionals are de facto educators of and advocates for the general public when it comes to ionizing radiation, who need to be fully conversant in the potential risks and benefits of medical procedures involving radiation.
The majority of this chapter will be devoted to so-called “foundational” radiobiology, that is, studies that largely predate the revolution in molecular biology and biotechnology during the 1980s and 1990s. While the reader might be tempted to view this body of knowledge as rather primitive by today's standards, relying too heavily on phenomenology, empiricism, and descriptive models and theories, the real challenge is to integrate the new biology into the already-existing framework of foundational radiobiology. Chapter 2 endeavors to do this.
Before examining any one aspect of radiobiology in depth, it is important to introduce several general concepts to provide a framework for putting the information in its proper perspective.
The most fundamental of these concepts is what is termed the therapeutic ratio—in essence, a risk-versus-benefit approach to planning a radiotherapy treatment regimen. Many of the radiobiological phenomena to be discussed in this chapter are thought to play important roles in optimizing, or at least “fine tuning,” the therapeutic ratio. In theory, it should be possible to eradicate any malignant tumor simply by delivering a sufficiently high dose of radiation. Of course, in practice, the biological consequences for normal tissues that are necessarily irradiated along with the tumor limit the total dose that can be safely administered. As such, a balance must be struck between what is deemed an acceptable probability of a radiation-induced complication in a normal tissue and the probability of tumor control. Ideally, one would hope to achieve the maximum likelihood of tumor control that does not produce unacceptable normal tissue damage.
The concept of therapeutic ratio is best illustrated graphically, by comparing dose-response curves for both tumor control and normal tissue complication rates plotted as a function of dose. Examples of this approach are shown in Fig. 1.1 for cases in which the therapeutic ratio is either “unfavorable,” “favorable,” or “optimal,” bearing in mind that these are theoretical curves. Actual dose-response curves derived from experimental or clinical data are much more variable, particularly for tumors, which tend to show much shallower dose responses. This serves to underscore how difficult it can be in practice to assign a single numerical value to the therapeutic ratio in any given situation.
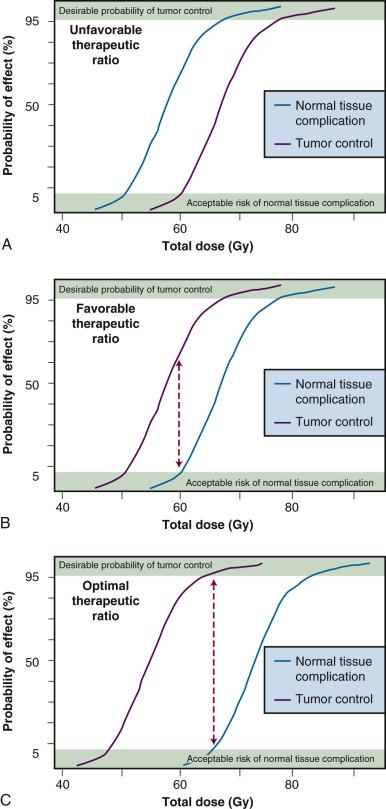
Many of the radiobiological properties of cells and tissues can have a favorable or adverse effect on the therapeutic ratio. Therefore, in planning a course of radiation therapy, the goal should be to optimize the therapeutic ratio as much as possible; in other words, using our graphical approach, increase the separation between the tumor control and normal tissue complication curves. This can be accomplished either by shifting the tumor control curve to the left with respect to the dose axis (toward lower doses, i.e., radiosensitization) or shifting the normal tissue complication curve to the right (toward higher doses, i.e., radioprotection) or, perhaps, some combination of both. The key, however, is to shift these curves differentially, not necessarily an easy task given that there are not that many exploitable differences in the radiobiology of cells derived from tumors and those derived from normal tissues.
There is a surprising continuity between the physical events that occur in the first few femtoseconds after ionizing radiation interacts with the atoms of a biomolecule and the ultimate consequences of that interaction on tissues. The consequences themselves may not become apparent until days, weeks, months, or even years after the radiation exposure. Some of the important steps in this radiobiology continuum are listed in Table 1.1 . The orderly progression from one stage of the continuum to the next—from physical to physicochemical to biochemical to biological—is particularly noteworthy not only because of the vastly different time scales over which the critical events occur but also because of the increasing biological complexity associated with each of the endpoints or outcomes. Each stage of the continuum also offers a unique radiobiological window of opportunity: the potential to intervene in the process and thereby modify all of the events and outcomes that follow.
| Time Scale of Events (“Stage”) |
Initial Event | Final Event | Response Modifiers/Possible Interventions |
|---|---|---|---|
| 10 −16 to 10 −12 second (“Physical”) | Ionization of atoms | Free radicals formed in biomolecules | Type of ionizing radiation; shielding |
| 10 −12 to 10 −2 second (“Physicochemical”) | Free radicals formed in biomolecules | DNA damage | Presence or absence of free radical scavengers, molecular oxygen and/or oxygen-mimetic radiosensitizers |
| 1.0 second to several hours (“Biochemical”) | DNA damage | Unrepaired or misrejoined DNA damage | Presence or absence of functioning DNA damage recognition and repair systems; repair-inhibiting drugs; altering the time required to complete repair processes |
| Hours to years (“Biological”) | Unrepaired or misrejoined DNA damage | Clonogenic cell death, apoptosis, mutagenesis, transformation, carcinogenesis, “early and late effects” normal tissues, whole body radiation syndromes, tumor control, etc. | Cell-cell interactions, biological response modifiers, adaptive mechanisms, structural and functional organization of tissues, cell kinetics, etc. |
Another important consideration in all radiobiological studies is the nature of the experimental system used to study a particular phenomenon, the assay(s) used, and the endpoint(s) assessed. For example, one investigator might be interested in studying DNA damage caused by ionizing radiation, in particular, the frequency of DNA double-strand breaks (DSBs) produced per unit dose. As an experimental system, the investigator might choose DNA extracted from irradiated mammalian cells and, as an endpoint, use pulsed field gel electrophoresis to measure the distance and rate at which irradiated DNA migrates through the gel compared with unirradiated DNA. The DNA containing more DSBs migrates farther than DNA containing fewer breaks, allowing a calibration curve to be generated that relates migration to the dose received. A second investigator, meanwhile, may be interested in improving the control rate of head and neck cancers with radiation therapy by employing a nonstandard fractionation schedule. In this case, the type of experiment would be a clinical trial. The experimental system would be a cohort of patients, some of whom are randomized to receive nonstandard fractionation and the rest receiving standard fractionation. The endpoints assessed could be one or more of the following: locoregional control, long-term survival, disease-free survival, normal tissue complication frequency, and so forth, evaluated at specific times after completion of the radiation therapy.
In considering both the strengths and weaknesses of these two investigators’ studies, any number of pertinent questions may be asked. Which is the more complex or heterogeneous system? Which is the more easily manipulated and controlled system? Which is more relevant for the day-to-day practice of radiation oncology? What kinds of results are gleaned from each and can these results be obtained in a timely manner? In this example, it is clear that human patients with spontaneously arising tumors represent a far more heterogeneous and complex experimental system than extracted mammalian DNA. However, the DNA system is much more easily manipulated, possible confounding factors can be more easily controlled, and the measurement of the desired endpoint (migration distance/rate) plus the data analysis can be completed within a day or two. Obviously, this is not the case with the human studies, in which numerous confounding factors can and do influence results, manipulation of the system can be difficult, if not impossible, and the experimental results typically take years to obtain.
The issue of relevance is an even thornier one. Arguably, both studies are relevant to radiation oncology in so far as the killing of cells is at the root of radiation’s normal tissue and tumor toxicity, and that cell killing usually is, directly or indirectly, a consequence of irreparable damage to DNA. As such, any laboratory findings that contribute to the knowledge base of radiation-induced DNA damage are relevant. Clearly, however, clinical trials with human patients not only are a more familiar experimental system to radiation oncologists but also, efficacy in conducting trials with cancer patients is ultimately what leads to new standards of care in clinical practice and becomes the gold standard against which all newer therapeutic strategies are judged.
There is a time and place both for relatively simple systems and more complex ones. The relatively simple, homogeneous, and easily manipulated systems are best suited for the study of the mechanisms of radiation action, such as measuring DNA or chromosomal damage, changes in gene expression, activation of cell cycle checkpoints, or the survival of irradiated cells in vitro. The more complicated and heterogeneous systems, with their unique endpoints, are more clinically relevant, such as assays of tumor control or normal tissue complication rates. Both types of assay systems have inherent strengths and weaknesses, yet both are critically important if we hope to improve the practice of radiation therapy based on sound biological principles.
Why is radiation therapy successful at controlling one patient's tumor but not another's when the two tumors in all other clinical respects seem identical? Why are we generally more successful at controlling certain types of cancers than others? The short answer to such questions is that, although the tumors may appear identical “macroscopically,” their component cells may be quite different genotypically and phenotypically. Also, there could be important differences between the two patients’ normal tissues.
Because normal tissues by definition are composed of more than one type of cell, they are necessarily heterogeneous. However, tumors, owing both to the genomic instability of individual cells and to microenvironmental differences, are much more so. Different subpopulations of cells isolated from human and experimental cancers can differ with respect to differentiation, invasive and metastatic potential, immunogenicity, and sensitivity to radiation and chemotherapy, to name but a few. (For reviews, see Heppner and Miller and Suit et al. ) This heterogeneity is manifest both within a particular patient and, to a much greater extent, between patients with otherwise similar tumors. Both intrinsic and extrinsic factors contribute to this heterogeneity. Intrinsic factors can include inherent radiosensitivity, genomic instability, gene expression patterns, DNA repair fidelity, mode(s) of cell death, cell cycle regulation, and how the tissue is structurally and functionally arranged. Extrinsic factors, on the other hand, are related to microenvironmental differences between tissues, such as the functionality of the vasculature, availability of oxygen and nutrients, pH, presence or absence of reactive oxygen species, cytokines and immune cells, energy charge, and cell-cell and cell-extracellular matrix interactions.
What are the practical implications of normal tissue and tumor heterogeneity? First, if one assumes that normal tissues are the more uniform and predictable in behavior of the two, then tumor heterogeneity is responsible, either directly or indirectly, for most radiotherapy failures. If so, this suggests that a valid clinical strategy might be to identify the radioresistant subpopulation(s) of tumor cells and then tailor therapy specifically to cope with them—although, admittedly, this approach is much easier said than done. Some clinical studies—both prospective and retrospective—now include one or more determinations of, for example, extent of tumor hypoxia or potential doubling time of tumor clonogens or specific tumor molecular/genetic factors. The hope is that these and other biomarkers can identify subsets of patients bearing tumors with different biological characteristics and that, accordingly, patients with particular characteristics can be assigned prospectively to different treatment groups.
Another consequence of tissue heterogeneity is that any radiobiological endpoint measured in an intact tissue necessarily reflects the sum total of the individual radiosensitivities of all of the subsets of cells, plus all other intrinsic and extrinsic factors that contribute to the overall response of the tissue. Since data on normal tissue tolerances and tumor control probabilities are also averaged across large numbers of patients, heterogeneity is even more pronounced.
Tumor control is achieved only when all clonogenic cells are killed or otherwise rendered unable to sustain tumor growth indefinitely. In order to estimate the likelihood of cure, it is necessary to know, or at least have an appreciation for, approximately how many clonogenic cells the tumor contains, how radiosensitive these cells are (i.e., some measure of killing efficiency per unit radiation dose), and what the relationship is between the number of clonogenic cells remaining after treatment and the probability of recurrence. The latter is perhaps the easiest to ascertain given our knowledge of both the random and discrete nature of radiation damage and the general shape of dose-response curves for mammalian cells and tissues. For a given number of surviving cells per tumor, the probability of local control can be derived from Poisson statistics using the equation P = e − n , where P is the tumor control probability and n is the average number of surviving clonogenic tumor cells. For example, when an average of one clonogenic cell per tumor remains at the end of radiation therapy, the tumor control rate will be about 37%. This means that about 6 out of 10 tumors of the same size and relative radiosensitivity will recur. Should the treatment reduce clonogenic cell numbers to an average of 0.1 per tumor, the tumor control probability would increase to 90%; 0.05 per tumor, 95%; and 0.01 per tumor, 99%, respectively.
The tumor control probability for a given fraction of surviving cells is not particularly helpful when the total number of cells at risk is unknown; this is where an understanding of logarithmic relationships and exponential cell killing is useful. For example, estimates are that a 1-cm 3 (1-g) tumor mass contains approximately 10 9 cells, admittedly a theoretical (and incorrect) value that assumes that all cells are perfectly packed and uniformly sized and that the tumor contains no stroma. A further assumption, that all such cells are clonogenic (rarely, if ever, the case), suggests that at least 9 logs of cell killing would be necessary before any appreciable tumor control (about 37%) would be achieved, and 10 logs of cell killing would be required for a high degree of tumor control (i.e., 90%).
After the first log or two of cell killing, however, some tumors respond by shrinking, a so-called partial response. After two to three logs of cell killing, the tumor may shrink to a size below the current limits of clinical detection, that is, a complete response. While partial and complete responses are valid clinical endpoints, a complete response does not necessarily equal a tumor cure. At least six more logs of cell killing would still be required before any significant probability of cure would be expected. This explains why radiation therapy is not halted if the tumor disappears during the course of treatment; this concept is illustrated graphically in Fig. 1.2 .
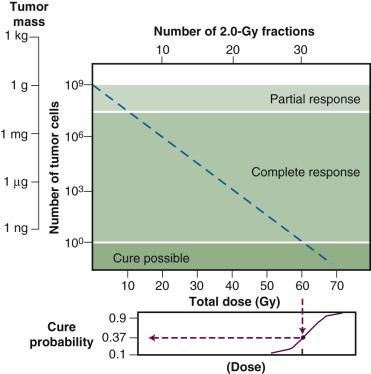
Finally, it should be noted that while the goal of curative radiation therapy is to reduce tumor cell survival by at least nine logs, even for the smallest tumor likely to be encountered, it is much less clear how many logs of cell killing a particular normal tissue can tolerate before it loses its structural and/or functional integrity. This would depend on how the tissue is organized structurally, functionally, and proliferatively, which constituent cells are the most and least radiosensitive, and which cells are the most important to the integrity of the tissue. It is unlikely, however, that many normal tissues could tolerate a depletion of two logs (99%) of their cells, let alone nine or more logs.
In fewer than 4 years after the discovery of x-rays by Roentgen, radioactivity by Becquerel, and radium by the Curies, the new modality of cancer treatment known as radiation therapy claimed its first cure of skin cancer. Today, more than 120 years later, radiotherapy is most commonly given as a series of small daily dose fractions of approximately 1.8 to 2.0 Gy each, 5 days per week, over a period of 5 to 7 weeks to total doses of 50 to 75 Gy. While it is true that the historical development of this conventional radiotherapy schedule was empirically based, there were a number of early radiobiological experiments that suggested this approach.
In the earliest days of radiotherapy, both x-rays and radium were used for cancer treatment. Due to the greater availability and convenience of using x-ray tubes and the higher intensities of radiation output achievable, it was fairly easy to deliver one or a few large doses in short overall treatment times. Thus, from about 1900 into the 1920s, this “massive dose technique” was a common way of administering radiation therapy. Normal tissue complications were often quite severe and, to make matters worse, the rate of local tumor recurrence was still unacceptably high.
Radium therapy was used more extensively in France. Because of the low activities available, radium applications necessarily involved longer overall treatment times in order to reach comparable total doses. Although extended treatments were less convenient, clinical results were often superior. Perceiving that the change in overall time was the critical factor, physicians began to experiment with the use of multiple, smaller x-ray doses delivered over extended periods. By that time, there was already a radiobiological precedent for expecting improvement in tumor control when radiation treatments were protracted.
As early as 1906, Bergonié and Tribondeau observed histologically that the immature, dividing cells of the rat testis showed evidence of damage at lower radiation doses than the mature, nondividing cells of the stroma. Based on these observations, they put forth some basic “laws” stating that x-rays were more effective on cells that were (1) actively dividing, (2) likely to continue to divide indefinitely, and (3) undifferentiated. Since tumors were already known to contain cells that were not only less differentiated but also exhibited greater mitotic activity, they reasoned that several radiation exposures might preferentially kill these tumor cells but not their slowly proliferating, differentiated counterparts in the surrounding normal tissues.
The end of common usage of the massive dose technique in favor of fractionated treatment came during the 1920s as a consequence of the pioneering experiments of Claude Regaud. Using the testes of the rabbit as a model tumor system (since the rapid and unlimited proliferation of spermatogenic cells simulated to some extent the pattern of cell proliferation in malignant tumors), Regaud showed that only through the use of multiple, smaller radiation doses could animals be completely sterilized without producing severe injury to the scrotum. Regaud suggested that the superior results afforded the multifraction irradiation scheme were related to alternating periods of relative radioresistance and sensitivity in the rapidly proliferating germ cells. These principles were soon tested in the clinic by Henri Coutard, who first used fractionated radiotherapy for the treatment of head and neck cancers, with spectacularly improved results, comparatively speaking. Largely as a result of these and related experiments, fractionated treatment subsequently became the standard form of radiation therapy.
Time-dose equivalents for skin erythema published by Reisner, Quimby and MacComb, and others formed the basis for the calculation of equivalents for other tissue and tumor responses. By plotting the total doses required for each of these “equivalents” for a given level of effect in a particular tissue, as a function of a treatment parameter—such as overall treatment time, number of fractions, dose per fraction, and so forth—an isoeffect curve could be derived. All time-dose combinations that fell along such a curve theoretically would produce tissue responses of equal magnitude. Isoeffect curves, relating the total dose to the overall treatment time, derived in later years from some of these data, are shown in Fig. 1.3 .
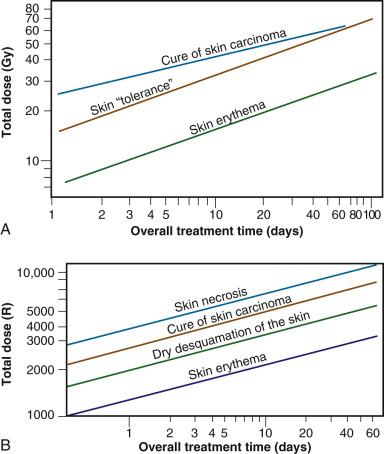
The first published isoeffect curves were produced by Strandqvist in 1944 and are also shown in Fig. 1.3 . When transformed on log-log coordinates, isoeffect curves for a variety of skin reactions and the cure of skin cancer were drawn as parallel lines, with common slopes of 0.33. These results implied that there would be no therapeutic advantage to using prolonged treatment times (i.e., multiple small fractions versus one, or a few, large doses) for the preferential eradication of tumors while simultaneously sparing normal tissues. It was somewhat ironic that the Strandqvist curves were so popular in the years that followed, when it was already known that the therapeutic ratio did increase (at least to a point) with prolonged, as opposed to very short, overall treatment times. However, the overarching advantage was that these isoeffect curves were quite reliable at predicting skin reactions, which were the dose-limiting factors at that time.
Perhaps the defining event that ushered in the golden age of radiation biology was the publication of the first survival curve for mammalian cells exposed to graded doses of x-rays. This first report of a quantitative measure of intrinsic radiosensitivity of a human cell line (HeLa, derived from a cervical carcinoma ) was published by Puck and Marcus in 1956. In order to put this seminal work in the proper perspective, it is first necessary to review the physicochemical basis for why ionizing radiation is toxic to biological materials.
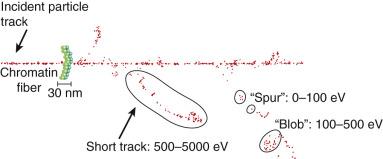
As mentioned in the introductory section of this chapter, ionizing radiation deposits energy as it traverses the absorbing medium through which it passes. The most important feature of the interaction of ionizing radiation with biological materials is the random and discrete nature of the energy deposition. Energy is deposited in increasingly energetic packets referred to as spurs (≤100 eV deposited), blobs (100–500 eV), or short tracks (500–5000 eV), each of which can leave from approximately three to several dozen ionized atoms in its wake. This is illustrated in Fig. 1.4 , along with a segment of (interphase) chromatin shown to scale. The frequency distribution and density of the different types of energy deposition events along the track of the incident photon or particle are measures of the radiation's linear energy transfer (LET; see also the “Relative Biological Effectiveness” section to come). Because these energy deposition events are discrete, it follows that while the average energy deposited in a macroscopic volume of biological material is small, the distribution of this energy on a microscopic scale may be quite large. This explains why ionizing radiation is so efficient at producing biological damage; the total amount of energy deposited in a 70-kg human that will result in a 50% probability of death is only about 70 calories, about as much energy as is absorbed by drinking one sip of hot coffee. The key difference is that the energy contained in the sip of coffee is uniformly distributed, not random and discrete.
Those biomolecules receiving a direct hit from a spur or blob receive, relatively speaking, a huge radiation dose, that is, a large energy deposition in a very small volume. For photons and charged particles, this energy deposition results in the ejection of orbital electrons from atoms, causing the target molecule to be converted first into an ion pair and then into a free radical. Further, the ejected electrons—themselves energetic charged particles—can go on to produce additional ionizations. For uncharged particles such as neutrons, the interaction is between the incident particles and the nuclei of the atoms in the absorbing medium, causing the ejection of recoil protons (charged) and lower-energy neutrons. The cycle of ionization, free radical production, and release of secondary charged particles continues until all of the energy of the incident photon or particle is expended. These interactions are complete within a picosecond after the initial energy transfer. After that time, the chemical reactions of the resulting free radicals predominate the radiation response (see later discussion).
Any and all cellular molecules are potential targets for the localized energy deposition events that occur in spurs, blobs, or short tracks. Whether the ionization of a particular biomolecule results in a measurable biological effect depends on a number of factors, including how probable a target the molecule represents from the point of view of the ionizing particle, how important the molecule is to the continued health of the cell, how many copies of the molecule are normally present in the cell and to what extent the cell can react to the loss of working copies, how important the cell is to the structure or function of its corresponding tissue or organ, and so on. DNA, for example, is obviously an important cellular macromolecule, and one that is present only as a single, double-stranded copy. On the other hand, other molecules in the cell may be less crucial to survival, yet are much more abundant than DNA and, therefore, have a much higher probability of being hit and ionized. By far, the most abundant molecule in the cell is water, comprising at least 70% to 80% of the cell on a per weight basis. The highly reactive free radicals formed by the radiolysis of water are capable of augmenting the DNA damage resulting from direct energy absorption by migrating to the DNA and damaging it indirectly. This mechanism is referred to as indirect radiation action to distinguish it from the aforementioned direct radiation action . The direct and indirect action pathways for ionizing radiation are illustrated below.
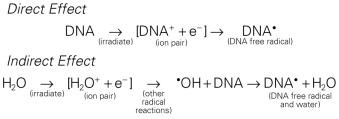
The most highly reactive and damaging species produced by the radiolysis of water is the hydroxyl radical ( • OH), although other free radical species are also produced in varying yields. Cell killing by indirect action constitutes some 70% of the total damage produced in DNA for low LET radiation.
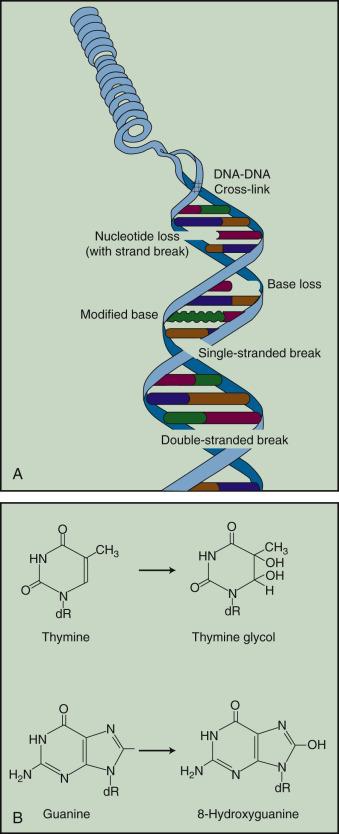
How do the free radicals produced by the direct and indirect action of ionizing radiation go on to cause the myriad lesions that have been identified in irradiated DNA? Since they contain unpaired electrons, free radicals are highly reactive chemically and will undergo multiple reactions in an attempt to either acquire new electrons or rid themselves of remaining unpaired ones. These reactions are considered quite slow compared with the time scale of the initial ionization events but are still fast relative to normal enzymatic processes in a typical mammalian cell. For all intents and purposes, free radical reactions are complete within milliseconds of irradiation. The • OH radical is capable of both abstraction of hydrogen atoms from other molecules and addition across carbon-carbon or other double bonds. More complex macromolecules that have been converted to free radicals can undergo a series of transmutations in an attempt to rid themselves of unpaired electrons, many of which result in the breakage of nearby chemical bonds. In the case of DNA, these broken bonds may result in the loss of a base or an entire nucleotide, or a frank scission of the sugar phosphate backbone, involving either one or both DNA strands. In some cases, chemical bonds are broken initially but then rearranged, exchanged, or rejoined in inappropriate ways. Bases in DNA may be modified by the addition of one or more hydroxyl groups (e.g., the base thymine converted to thymine glycol), pyrimidines may become dimerized, and/or the DNA may become cross-linked to itself or to associated proteins. Again, because the initial energy deposition events are discrete, the free radicals produced also are clustered and, therefore, undergo their multiple chemical reactions and produce multiple damages in a highly localized area. This has been termed the locally multiply damaged site or cluster hypothesis. Examples of the types of damage found in irradiated DNA are shown in Fig. 1.5 .
DNA is unique insofar as it is the only cellular macromolecule with its own repair system. Until as recently as 35 years ago, little was known about DNA repair processes in mammalian cells, particularly because of the complexities involved and the relative lack of spontaneously occurring mutants defective in genes involved with DNA repair. As a consequence, most studies of DNA repair were carried out either in bacteria or yeasts and usually employed UV radiation as the tool for producing DNA damage. Although these were rather simple and relatively clean systems in which to study DNA repair, their relevance to mammalian repair systems and to the broader spectrum of DNA damage produced by ionizing radiation ultimately limited their usefulness.
The study of DNA repair in mammalian cells received a significant boost during the late 1960s with publications by Cleaver that identified the molecular defect responsible for the human disease xeroderma pigmentosum (XP). Patients with XP are exquisitely sensitive to sunlight and highly (skin) cancer prone. Cleaver showed that cells derived from such patients were likewise sensitive to UV radiation and defective in the nucleotide excision repair pathway (see later discussion). These cells were not especially sensitive to ionizing radiation, however. Several years later, Taylor et al . reported that cells derived from patients with a second cancer-proneness disorder called ataxia telangiectasia (AT) were extremely sensitive to ionizing radiation and radiation-mimetic drugs, but not UV. In the years that followed, cell cultures derived from patients with these two conditions were used to help elucidate the complicated processes of DNA repair in mammalian cells. Today, dozens of other clinical syndromes associated with radiosensitivity, cancer proneness, or both have been identified.
Today, many rodent and human genes involved in DNA repair have been cloned and extensively characterized. Some 30 to 40 proteins participate in excision repair of base damage; about half that many are involved in the repair of strand breaks. Many of these proteins function as component parts of larger repair complexes. Some are interchangeable and participate in other DNA repair and replication pathways as well. It is also noteworthy that some are not involved with the repair process per se, but rather link DNA repair to other cellular functions, including transcription, cell cycle arrest, chromatin remodeling, and apoptosis. This attests to the fact that the maintenance of genomic integrity results from a complex interplay between not only the repair proteins themselves but also others that serve as damage sensors, signaling mediators and transducers, and effectors. Collectively, this complex network of proteins that sense, initiate, and coordinate DNA damage signaling and repair with other cellular activities is termed the DNA Damage Response (DDR). For example, the defect responsible for the disease AT is not in a gene that codes for a repair protein but rather in a gene that acts in part as a damage sensor and signal transducer but also participates in a related pathway that normally prevents cells from entering S phase and beginning DNA synthesis while residual DNA damage is present. This is termed the G 1 cell cycle checkpoint response. Because of this genetic defect, AT cells do not experience the normal G 1 arrest after irradiation and enter S phase with residual DNA damage. This accounts both for the exquisite radiosensitivity of AT cells and the resulting genomic instability that can lead to cancer.
The molecular and biochemical intricacies of DNA repair in mammalian cells are described in detail in Chapter 2 . A brief overview is also presented next.
The repair of base damage is initiated by DNA repair enzymes called glycosylases , which recognize specific types of damaged bases and excise them without otherwise disturbing the DNA strand. The action of the glycosylase results in the formation of another type of damage observed in irradiated DNA—an apurinic or apyrimidinic (AP) site. The AP site is then recognized by another repair enzyme, an endonuclease that nicks the DNA adjacent to the lesion, in effect creating a DNA single-stranded break. This break then becomes the substrate for an exonuclease, which removes the abasic site, along with a few additional bases. The small gap that results is patched by DNA polymerase using the opposite, hopefully undamaged, DNA strand as a template. Finally, DNA ligase seals the patch in place.
The DNA glycosylases that begin the process of base excision repair do not recognize all known forms of base damage, however, particularly bulky or complex lesions. In such cases, another group of enzymes, termed structure-specific endonucleases , initiate the excision repair process. These repair proteins do not recognize the specific lesion but rather the structural distortions in DNA that necessarily accompany a complex base lesion. The structure-specific endonucleases incise the affected DNA strand on both sides of the lesion, releasing an oligonucleotide fragment made up of the damage site and several bases on either side of it. After this step, the remainder of the nucleotide excision repair process is similar to that of base excision repair. The gap is then filled by DNA polymerase and sealed by DNA ligase.
For both types of excision repair, active genes in the process of transcription are repaired preferentially and more quickly. This has been termed transcription-coupled repair .
Single-strand breaks (SSBs) in the DNA backbone are common lesions, produced in the tens of thousands per cell per day as part of normal metabolism and respiration on top of any additional breaks introduced by radiation exposure. These are repaired using the machinery of excision repair, that is, gap filling by DNA polymerase and sealing by DNA ligase.
Despite the fact that unrepaired or misrejoined double-strand breaks (DSBs) often have the most catastrophic consequences for the cell in terms of loss of reproductive integrity, how mammalian cells repair these lesions has been more difficult to elucidate than how they repair base damage. Much of what was originally discovered about these repair processes is derived from studies of x-ray-sensitive rodent cells that were later discovered to harbor specific defects in strand break repair. Since then, dozens of other rodent and human cells characterized by DDR defects have been identified and are also used to help probe these fundamental processes.
With respect to the repair of DSBs, the situation is more complicated in that the damage on each strand of DNA may be different and, therefore, no intact template would be available to guide the repair process. Under these circumstances, cells must rely on a somewhat error-prone process that rejoins the break(s) regardless of the loss of intervening base pairs for which there is no template (nonhomologous end joining [NHEJ]) or depend on genetic recombination in which a template for presumably error-free repair is obtained from recently replicated DNA of a sister chromatid (homologous recombination [HR] ) to cope with the damage. NHEJ occurs throughout the cell cycle, but predominates in cells that have not yet replicated their DNA, that is, cells in the G 1 or G 0 phases of the cell cycle. NHEJ involves a heterodimeric enzyme complex consisting of the proteins Ku-70 and Ku-80, the catalytic subunit of DNA protein kinase (DNA-PK CS ), and DNA ligase IV. Cells that have already replicated most or all of their DNA—in the late S or G 2 phases of the cell cycle—depend on HR to repair DSBs. HR involves the assembly of a nucleoprotein filament that contains, among others, the proteins Rad51 and Rad52. This filament then invades the homologous DNA sequence of a sister chromatid, which becomes the template for repair. The BRCA2 protein is also implicated in HR as it interacts with the Rad51 protein. Defects in either the BRCA1 (which helps determine which DSB repair pathway will be used in a particular situation) or BRCA2 genes are associated with hereditary breast and ovarian cancer.
The primary role of mismatch repair (MMR) is to eliminate from newly synthesized DNA errors such as base/base mismatches and insertion/deletion loops caused by DNA polymerase. This process consists of three steps: mismatch recognition and assembly of the repair complex, degradation of the error-containing strand, and repair synthesis. In humans, MMR involves at least five proteins, including hMSH2 and hMLH1, as well as other members of the DNA repair and replication machinery.
Radiation-induced DNA lesions are not targets for mismatch repair per se. However, one manifestation of a defect in mismatch repair is germane to any study of oncogenesis: genomic instability, which renders affected cells hypermutable. This “mutator phenotype” is associated with several cancer predisposition syndromes, in particular, hereditary nonpolyposis colon cancer (HNPCC, a.k.a. Lynch syndrome). Genomic instability is considered one of the main enablers of normal cells to accumulate cancer-causing mutations and also drives tumor progression to more aggressive and potentially treatment-resistant phenotypes.
Historically, attempts to inhibit the repair of radiation-induced DNA damage were of interest to researchers probing these fundamental processes. However, clinical translation was typically lacking, mostly out of concern that normal tissues would also be affected in an adverse way. More recently, it has become clear that the cells of many tumors harbor one or more defects in the DDR (as a consequence of genomic instability) that are not present in normal cells and that this difference might be exploitable clinically.
One approach along these lines is the use of inhibitors of the protein poly(ADP-ribose) polymerase (PARP). As of 2018, dozens of trials were underway using PARP inhibitors in combination with chemo- and immunotherapies. PARP is a damage sensor involved in both base excision and SSB repair that, if inhibited, leads to the persistence of SSBs. If left unrejoined, these breaks can cause the collapse of replication forks in DNA that then impede DNA replication, transcription, and HR repair, leading to radiosensitization and, ultimately, cell death.
In normal cells, little or no toxicity caused by PARP inhibition would be expected, as all DDR pathways are intact and salvage repair pathways to bypass PARP inhibition are active. In tumor cells already harboring defects in HR, however, PARP inhibition would be preferentially toxic. One clinical example is the targeting of breast cancers harboring cellular defects in the BRCA1/2 proteins—which either orchestrate or are directly involved in HR—for PARP inhibition. This overall approach of using the combined lethal effect of two genetic defects (one inherent HR defect plus one synthetic one induced by PARP inhibition) that are otherwise nonlethal singly is termed synthetic lethality . Synthetic lethality approaches targeting DDR proteins (including those other than PARP) likely will play increasingly important roles in the future.
When cells divide following radiation exposure, chromosomes frequently contain visible structural aberrations that are the result of any unrepaired or misrejoined DNA damage that persists from the time of irradiation. Most chromosome aberrations are lethal to the cell. In some cases, these aberrations physically interfere with the processes of mitosis and cytokinesis, resulting in prompt cell death. In other cases, cell division can occur but the loss or uneven distribution of genetic material between the cell's progeny is ultimately lethal as well, although the affected cells may linger for several days before they die, with some even be able to go through a few more cell divisions in the interim.
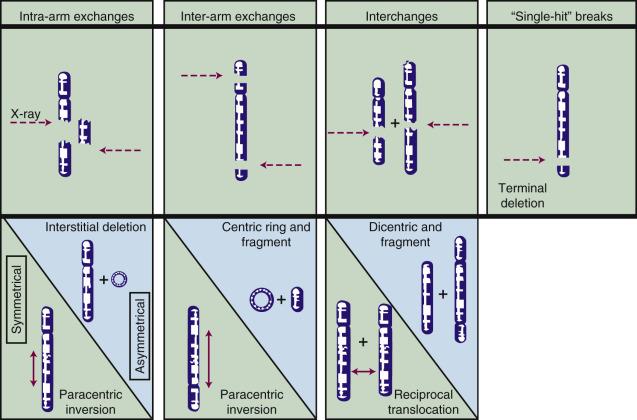
Most chromosome aberrations result from an interaction between two damage sites; therefore, they can be grouped into three different types of “exchange” categories. A fourth category is reserved for those chromosome aberrations that are thought to result from a single damage site. These categories are described here; representative types of aberrations from each category are shown in Fig. 1.6 :
Intra-arm Exchanges: An interaction between lesions on the same arm of a single chromosome (example: interstitial deletion).
Inter-arm Exchanges: An interaction between lesions on opposite arms of the same chromosome (example: centric ring).
Interchanges: An interaction between lesions on different chromosomes (example: dicentric).
“Single Hit” Breaks: The complete severance of part of one arm of a single chromosome not obviously associated with any more than a single lesion (example: terminal deletion).
These four categories can be further subdivided according to whether the initial radiation damage occurred before or after the DNA is replicated (a chromosome- vs. chromatid-type aberration, respectively) and, for the three exchange categories, whether the lesion interaction is symmetrical or asymmetrical. Asymmetrical exchanges always lead to the formation of acentric fragments that are usually lost in subsequent cell divisions and, therefore, are nearly always fatal to the cell. These fragments may be retained transiently in the cell's progeny as extranuclear chromatin bodies called micronuclei . Symmetrical exchanges are more insidious in that they do not lead to the formation of acentric fragments and the accompanying loss of genetic material at the next cell division; thus, they do not always kill the cell. As such, they will be transmitted to all progeny of the original cell. Some types of symmetrical exchanges (e.g., a reciprocal translocation) have been implicated in radiation carcinogenesis insofar as they have the net effect of either bringing new combinations of genes together or separating preexisting groups of genes. Depending on where in the genome the translocation takes place, genes normally active could be turned off or vice versa, potentially with adverse consequences.
Quantitation of the types and frequencies of chromosome aberrations in irradiated cells can be used to probe dose-response relationships for ionizing radiation and, to a first approximation, also can serve as a radiation dosimeter. For example, the dose-response curve for the induction of exchange-type aberrations after exposure to low-LET radiation tends to be linear-quadratic in shape, whereas that for single-hit aberrations tends to be linear. In mathematical terms, the incidence, I, of a particular aberration as a function of radiation dose, D, can be expressed as
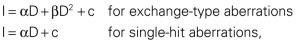
where α and β are proportionality constants related to the yields of the particular type of aberration and c is the spontaneous frequency of that aberration in unirradiated cells. For fractionated doses or continuous low dose rates of low-LET radiation, the yield of exchange-type aberrations decreases relative to that for acute doses, and the dose-response curve becomes more linear. For high-LET radiations, dose-response curves become steeper (higher aberration yields per unit dose) and more linear compared with those for low-LET radiations.
The traditional definition of death as a permanent, irreversible cessation of vital functions is not the same as what constitutes “death” to the radiation biologist or oncologist. For proliferating cells—including those maintained in vitro, the stem cells of normal tissues, and tumor clonogens—cell death in the radiobiological sense refers to a loss of reproductive integrity, that is, an inability to sustain proliferation indefinitely. This type of “reproductive” or “clonogenic” death does not preclude the possibility that a cell may remain physically intact, metabolically active, and continue its tissue-specific functions for some time after irradiation.
Compared with nearly 65 years ago, when the term clonogenic death was first coined and used as an endpoint in assays of cellular radiosensitivity, by today's standards it is clearly an operationally defined term that encompasses several distinct mechanisms by which cells die, all of which result in a cell losing its ability to divide indefinitely. These modes of cell death include mitotic catastrophe, apoptosis, necrosis, senescence, and autophagy. Strictly speaking, differentiation is included as well, because differentiated cells lose their ability to divide.
Mitotic catastrophe is the major mode of radiation-induced death for most mammalian cells, occurring secondary to chromosome aberrations and/or spindle defects that interfere with the cell division process. Accordingly, this type of cell death occurs during or soon after an attempted cell division postirradiation (although not necessarily during the very first division attempt), leaving in its wake large, flattened, and multinucleated cells that are typically aneuploid. Apoptosis, or programmed cell death, is a type of nonmitotic or interphase death commonly associated with embryonic development and normal tissue remodeling and homeostasis. However, certain normal tissue and tumor cells also undergo apoptosis following irradiation, including normal cells of hematopoietic or lymphoid origin, crypt cells of the small intestine, salivary gland cells, plus a few tumor cell lines of gynecological and hematological origin. Cells undergoing apoptosis exhibit a number of characteristic morphological (nuclear condensation and fragmentation, membrane blebbing, etc.) and biochemical (DNA degradation) changes that culminate in the fragmentation of the cell, typically within 12 to 24 hours of irradiation and prior to the first postirradiation mitosis. The remains of apoptotic cells are phagocytized by neighboring cells; therefore, they do not elicit the type of inflammatory response, tissue destruction, and disorganization characteristic of necrosis. Apoptosis is an active and carefully regulated pathway that involves multiple proteins and an appropriate stimulus that activates the pathway. The molecular biology of apoptosis, the apoptosis-resistant phenotype noted for many types of tumor cells, and the role that radiation may play in the process are discussed in detail in Chapter 2 . Senescence refers to a type of genetically controlled cellular growth arrest that, while not necessarily eliminating damaged cells, does halt permanently their continued movement through the cell cycle even in the presence of growth factors. Radiation can also induce senescence, presumably due to the permanent triggering of cell cycle checkpoints. However, it might better be termed radiation-induced permanent growth arrest to distinguish it from the normal process of cell age-related senescence. Autophagy is defined as the controlled lysosomal degradation of cytoplasmic organelles or other cytoplasmic components in response to cellular stressors, including nutrient deprivation, hypoxia, DNA damage, or an excess of reactive oxygen species. Likewise, necrosis—characterized by cell swelling followed by membrane rupture and the release of cellular contents into the extracellular space—can occur as a somewhat passive response to nutrient deprivation but also can follow a molecular program initiated by immune cells or various toxins.
Most assays of radiosensitivity of cells and tissues, including those described later, use reproductive integrity, either directly or indirectly, as an endpoint. While such assays have served the radiation oncology community well in terms of elucidating dose-response relationships for normal tissues and tumors, the interrelationships between the different modes of cell death can be quite complex. For example, Meyn has suggested that a tumor with a high spontaneous apoptotic index may be inherently more radiosensitive because cell death might be triggered by lower doses than are usually required to cause mitotic catastrophe. Also, tumors that readily undergo apoptosis may have higher rates of cell loss, the net effect of which would be to partially offset cell production, thereby reducing the number of tumor clonogens. On the other hand, recent studies suggest that the very enzymes that orchestrate the removal of radiation-damaged cells via apoptosis also may stimulate tumor cell repopulation during and after radiotherapy. Studies also suggest that senescent cells can produce inflammatory cytokines that further contribute to immunosuppression in the tumor microenvironment.
Survival curve theory originated in a consideration of the physics of energy deposition in matter by ionizing radiation. Early experiments with macromolecules and prokaryotes established that dose-response relationships could be explained by the random and discrete nature of energy absorption if it was assumed that the response resulted from critical “targets” receiving random “hits.” With an increasing number of shouldered survival and dose-response curves being described for cells irradiated both in vitro and in vivo, various equations were developed to fit these data. Target theory pioneers studied a number of different endpoints in the context of target theory, including enzyme inactivation in cell-free systems, cellular lethality, chromosomal damage, and radiation-induced cell cycle perturbations in microorganisms. Survival curves, in which the log of the “survival” of a certain biological activity was plotted as a function of the radiation dose, were found to be either exponential or sigmoid in shape, the latter usually noted for the survival of more complex organisms.
Exponential survival curves were thought to result from the single-hit, “all or nothing” inactivation of a single target, resulting in the loss of activity. A mathematical expression used to fit this type of dose-response relationship is
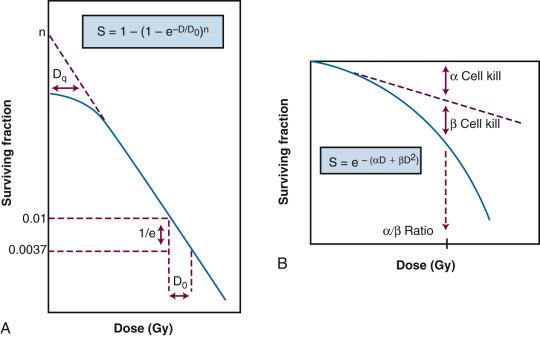
In this equation, S is the fraction of cells that survive a given dose, D, and D 0 is the dose increment that reduces the cell survival to 37% (1/e) of some initial value on the exponential portion of the curve (i.e., a measure of the reciprocal of the slope). Target theory could also be applied to survival curves with shoulders at low doses if one assumed that either multiple targets or multiple hits in a single target were necessary for radiation inactivation. A mathematical expression based on target theory that provided a fairly good fit to survival data was
with n being the back extrapolation of the exponential portion of the survival curve to zero dose. Implicit in this multitarget model was that damage had to accumulate before the overall effect was registered.
It soon became apparent that some features of this model were inadequate. The most obvious problem was that the single-hit, multitarget equation predicted that survival curves should have initial slopes of zero, that is, that for vanishingly small doses (e.g., repeated, small doses per fraction or continuous low dose rate exposure), the probability of cell killing would approach zero. This is not what was observed in practice for either mammalian cell survival curves or as inferred from clinical studies in which highly fractionated or low dose rate treatment schedules were compared to more conventional fractionation. There was no fractionation schedule that produced essentially no cell killing, all other radiobiological factors being equal.
A somewhat different interpretation of cell survival was proposed by Kellerer and Rossi in the late 1960s and early 1970s. The linear-quadratic or “alpha-beta” equation,
was shown to fit many survival data quite well, particularly in the low-dose region of the curve, and also provided for the negative initial slope that investigators had described. In this expression, S is again the fractional cell survival following a dose D, α is the rate of cell kill by a single-hit process, and β is the rate of cell kill by a two-hit mechanism. The theoretical derivation of the linear-quadratic equation is based on two sets of observations. Based on microdosimetric considerations, Kellerer and Rossi proposed that a radiation-induced lethal lesion resulted from the interaction of two sublesions. According to this interpretation, the αD term is the probability of these two sublesions being produced by a single event (the “intra-track” component), whereas βD 2 is the probability of the two sublesions being produced by two separate events (the “inter-track” component). Chadwick and Leenhouts derived the same equation based on a different set of assumptions, namely, that a DSB in DNA was a lethal lesion and that such a lesion could be produced by either a single energy deposition involving both strands of DNA or by two separate events, each involving a single strand.
A comparison of the features and parameters of the target theory and linear-quadratic survival curve expressions is shown in Fig. 1.7 .
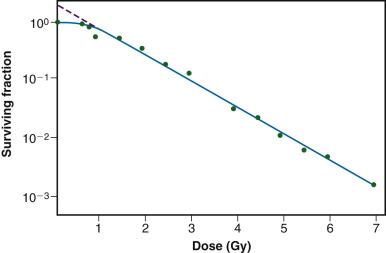
As mentioned previously, it was not until the mid-1950s that mammalian cell culture techniques were sufficiently refined to allow quantitation of the radiation responses of single cells. Puck and Marcus's acute dose, x-ray survival curve for the human tumor cell line HeLa is shown in Fig. 1.8 . Following graded x-ray doses, the reproductive integrity of single HeLa cells was measured by their ability to form macroscopic colonies of at least 50 cells (corresponding to approximately 6 successful postirradiation cell divisions) on petri dishes. Several features of this survival curve were of particular interest. First, qualitatively at least, the curve was similar in shape to those previously determined for many microorganisms, being characterized by a shoulder at low doses and a roughly exponential region at high doses. Of note, however, was the finding that the D 0 for HeLa cells was only 96 R, some 10- to 100-fold less than D 0 s determined for microorganisms and 1000- to 10,000-fold less than D 0 s for the inactivation of isolated macromolecules. Thus, cellular reproductive integrity was found to be a much more radiosensitive endpoint for HeLa cells than for prokaryotes or primitive eukaryotes. The value of the extrapolation number, n, was approximately 2.0, indicating that the survival curve did have a small shoulder but, again, much smaller than typically observed for microorganisms. Puck and Marcus suggested that the n value was a reflection of the number of critical targets in the cell, each requiring a single hit before the cell would be killed, and further postulated that the targets were, in fact, the chromosomes themselves. However, the potential pitfalls of deducing mechanisms of radiation action from parameters of a descriptive survival curve model were soon realized.
Survival curves for other types of mammalian cells, regardless of whether they were derived from humans or laboratory animals, or from tumors or normal tissues, have been shown to be qualitatively similar to the original HeLa cell survival curve.
In order to bridge the gap between the radiation responses of cells grown in culture and in an animal, Hewitt and Wilson developed an ingenious method to assay single-cell survival in vivo. Lymphocytic leukemia cells obtained from the livers of donor CBA mice were harvested, diluted, and inoculated into disease-free recipient mice. By injecting different numbers of donor cells, a standard curve was constructed that allowed a determination of the average number of injected cells necessary to cause leukemia in 50% of the recipient mice. It was determined that the endpoint of this titration, the 50% take dose (TD 50 ), corresponded to an inoculum of a mere two leukemia cells. Using this value as a reference, Hewitt and Wilson then injected leukemia cells harvested from γ-irradiated donor mice into recipients and again determined the TD 50 following different radiation exposures. In this way, the surviving fraction after a given radiation dose could be calculated from the ratio of the TD 50 for unirradiated cells to that for the irradiated cells. Using this technique, a complete survival curve was constructed that had a D 0 of 162 R and an n value close to 2.0, values quite similar to those generated for cell lines irradiated in vitro. For the most part, in vivo survival curves for a variety of cell types were also similar to corresponding in vitro curves.
A similar trend was apparent when in vivo survival curves for nontumorigenic cells were first produced. The first experiments by Till and McCulloch using normal bone marrow stem cells were inspired by the knowledge that failure of the hematopoietic system was a major cause of death following total body irradiation and that lethally irradiated animals could be “rescued” by a bone marrow transplant. The transplanted, viable bone marrow cells were observed to form discrete nodules or colonies in the otherwise sterilized spleens of irradiated animals. Subsequently, these authors transplanted known quantities of irradiated donor bone marrow into lethally irradiated recipient mice. They were able to count the resulting splenic nodules and then calculate the surviving fraction of the injected cells in much the same way as was done for in vitro experiments. The D 0 for mouse bone marrow was 0. 95 Gy. Other in vivo assay systems based on the counting of colonies or nodules included the skin epithelium assay of Withers, the intestinal crypt assays of Withers and Elkind, and the lung colony assay of Hill and Bush. During the late 1960s and early 1970s, it also became possible to do excision assays, in which tumors irradiated in vivo were removed, enzymatically dissociated, and single cells plated for clonogenic survival in vitro. This allowed more quantitative measurement of survival, avoiding some of the pitfalls of in vivo assays (e.g., Rockwell and Kallman ).
Some normal tissues and tumors are not amenable to clonogenic assays. Thus, new assays were needed that had clinical relevance yet did not rely on reproductive integrity as an endpoint. Use of such assays required one leap of faith—namely, that the endpoints assessed would have to be a consequence of the killing of clonogenic cells, although not necessarily in a direct, one-to-one manner. Because nonclonogenic assays do not directly measure cell survival as an endpoint, data derived from them and plotted as a function of radiation dose are properly called dose-response curves rather than cell survival curves, although such data are often analyzed and interpreted similarly.
Historically, among the first nonclonogenic assays was the mean lethal dose or LD 50 assay, in which the (whole body) radiation dose to produce lethality in approximately 50% of the test subjects is determined, usually at a fixed time after irradiation, such as 30 (LD 50/30 ) or 60 days (LD 50/60 ). Clearly, the LD 50 assay is not very specific in that the cause of death can result from damage to a number of different tissues.
Another widely used nonclonogenic method to assess normal tissue radioresponse is the skin reaction assay, originally developed by Fowler et al. Pigs were often used because their skin is similar to that of humans in several respects. An ordinate scoring system was used to compare and contrast different radiation schedules, which was derived from the average severity of the skin reaction noted during a certain time period (specific to the species and whether the endpoint occurs early or late) following irradiation. For example, for early skin reactions, a skin score of 1 might correspond to mild erythema, whereas a score of 4 might correspond to confluent moist desquamation over more than half of the irradiated area.
Finally, two common nonclonogenic assays for tumor response are the growth delay/regrowth delay assay and the tumor control dose assay. Both assays are simple and direct, are applicable to most solid tumors, and are clinically relevant. The growth delay assay involves measurements of a tumor's dimensions or volume as a function of time after irradiation. For tumors that regress rapidly during and after radiotherapy, the endpoint scored is typically the time in days that it takes for the tumor to regrow to its original volume at the start of irradiation. For tumors that regress more slowly, a more appropriate endpoint might be the time that it takes for the tumor to grow or regrow to a specified size, such as three times its original volume. Dose-response curves are generated by plotting the amount of growth delay as a function of radiation dose.
The tumor control assay is a logical extension of the growth delay assay. The endpoint of this assay is the total radiation dose required to achieve a specified probability of local tumor control—usually 50% (TCD 50 )—in a specified period of time after irradiation. The TCD 50 value is obtained from a plot of the percentage of tumors locally controlled as a function of total dose. The slope of the resulting dose-response curve may be used for comparative purposes as a measure of the tumor's inherent “radiosensitivity” and/or its degree of heterogeneity. More heterogeneous tumors tend to have shallower dose response curves than more homogeneous ones, as do spontaneous tumors relative to experimental ones maintained in inbred strains of mice.
Taking the cue from target theory that the shoulder region of the radiation survival curve indicated that “hits” had to accumulate prior to cell killing, Elkind and Sutton sought to better characterize the nature of the damage caused by these hits and how the cell processed this damage. Even in the absence of any detailed information about DNA damage and repair at the time, a few things seemed obvious. First, those hits or damages that were registered as part of the accumulation process yet did not in and of themselves produce cell killing were, by definition, sublethal. Second, sublethal damage (SLD) became lethal only when it interacted with additional sublethal damage, that is, when the total amount of damage had accumulated to a sufficient level to cause cell killing. But what would be the result of deliberately interfering with the damage accumulation process by, for example, delivering part of the intended radiation dose, inserting a radiation-free interval, and then delivering the remainder of the dose? The results of such “split-dose” experiments turned out to be crucial to the understanding of why and how fractionated radiation therapy works as it does. The discovery and characterization of SLD, as low tech and operational the concept may be by today's standards, still stands as arguably the single most important contribution that radiation biology has made to the practice of radiation oncology.
By varying the time interval between two doses of approximately 5.0 Gy and plotting the log of the surviving fraction of cells after both doses (i.e., 10 Gy total dose) as a function of the time between the doses, the resulting split-dose recovery curve was observed to rise to a maximum after about 2 hours and then level off. In other words, the overall surviving fraction of cells following 10 Gy was higher if the dose was split into two fractions with a time interval in between than delivered as a single dose. Elkind interpreted these results as indicating that the cells that survived the initial dose fraction had “repaired” some of the damage during the radiation-free interval and, as such, this damage was no longer available to interact with the damage inflicted by the second dose. At the time, Elkind referred to this phenomenon as sublethal damage repair (SLDR). In retrospect, it is perhaps preferable to call it sublethal damage recovery , since biochemical DNA repair processes were not actually measured, only changes in cell survival.
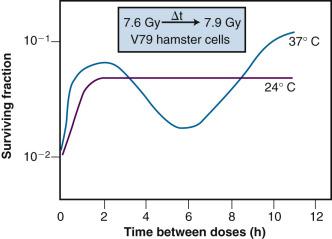
Of additional interest was the observation that the shape of the split-dose recovery curve varied with the temperature during the radiation-free interval ( Fig. 1.9 ). When the cells were maintained at room temperature between the split doses, the SLDR curve rose to a maximum after about 2 hours and then leveled off. When the cells were returned to a 37° C incubator for the radiation-free interval, a different pattern emerged. Initially, the split-dose recovery curve rose to a maximum after 2 hours; then, the curve exhibited a series of oscillations, dropping to a second minimum for a split of about 4 to 5 hours, and then rising again to a higher maximum for split-dose intervals of 10 hours or more. The interpretation of this pattern of SLDR was that other radiobiological phenomena operated simultaneously with cellular recovery. In this case, the fine structure of the split-dose recovery curve was not caused by an oscillating repair process but rather by a superimposed cell cycle effect: the so-called radiation “age response” through the cell cycle. This is discussed later in the “Ionizing Radiation and the Cell Cycle” section (see also Fig. 1.14 ).
Since Elkind and Sutton's original work, SLDR kinetics have been described for many different types of mammalian cells in culture, and for most normal and tumor tissues in vivo (e.g., Belli et al. and Emery et al. ). Pertinent findings include the following:
The amount of SLD capable of being repaired for a given cell type varies both with the radiation quality (less for radiations of increasing LET) and the oxygenation status of the cells (recovery reduced or absent at extremely low oxygen tensions).
The half-time for SLDR in mammalian cells in culture is, on average, about 1 hour, although there is evidence that it may be somewhat longer for late-responding normal tissues in vivo.
The survival increase between split doses is a manifestation of the “regeneration” of the shoulder of the radiation survival curve. After an initial radiation dose and an adequate time interval for SLDR, the response of surviving cells to graded additional doses is nearly identical to that obtained from cells without previous radiation exposure. Thus, the width of the shoulder of the survival curve came to be associated with the capacity of the cells for recovery from sublethal damage. This concept is illustrated in Fig. 1.10 .
Cells are able to undergo repeated cycles of damage and recovery without a change in recovery capacity. As such, one would predict an equal effect per dose fraction during the course of fractionated radiotherapy. In a more practical sense, this means that a multifraction survival curve can be generated using the formula SF n = (SF 1 ) n , where SF 1 is the surviving fraction of cells after a single-dose fraction (determined from a single-dose survival curve), and SF n is the surviving fraction of cells after n dose fractions. Accordingly, multifraction survival curves are shoulderless and exponential ( Fig. 1.11 ).
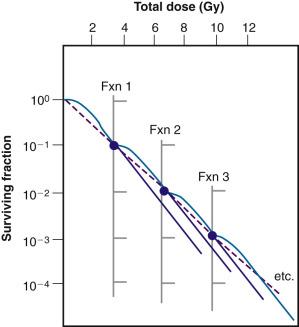
Sublethal damage recovery is largely responsible for the dose rate effect for low-LET radiation, which will be discussed in detail later in this chapter. As the dose per fraction (intermittent radiation) or dose rate (continuous irradiation) is decreased and the overall treatment time increased, the biological effectiveness of a given total dose is reduced. (Note that SLDR also occurs during continuous irradiation, i.e., that a radiation-free interval is not required per se.)
A second type of cellular recovery following irradiation is termed potentially lethal damage repair or recovery (PLDR), and was first described for mammalian cells by Phillips and Tolmach in 1966. PLD is, by definition, a spectrum of radiation damage that may or may not result in cell killing depending on the cell's postirradiation environment. Environmental conditions that favor PLDR include maintenance of cells in overcrowded conditions (plateau phase or contact-inhibited ) and incubation following irradiation at either reduced temperature in the presence of certain metabolic inhibitors or in balanced salt solutions rather than complete culture medium. What these treatment conditions have in common is that they are suboptimal for continued growth of cells. This gives resting cells more opportunity to repair DNA damage prior to cell division than cells that continue traversing the cell cycle immediately after irradiation. Phillips and Tolmach were the first to propose this repair-fixation or competition model to explain PLDR.
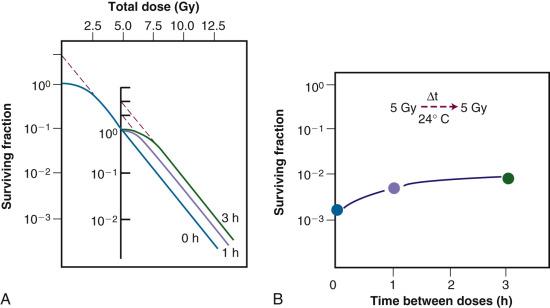
While, admittedly, some of these postirradiation conditions are not likely to be encountered in vivo, slow growth of cells in general, with or without a large fraction of resting cells, is a common characteristic of many tissues. As might be expected, tumors (and, subsequently, select normal tissues amenable to clonogenic assay) were shown to repair PLD. Experiments using rodent tumors were modeled after comparable studies using plateau phase cells in culture, that is, a delayed-plating assay was used. For such an experiment, irradiated cell cultures or animal tumors are left in a confluent state (either in the overcrowded cell culture or in the intact tumor in the animal) for varying lengths of time before removing them, dissociating them into single-cell suspensions and plating the cells for clonogenic survival at a low density. The longer the delay between irradiation and the clonogenic assay, the higher the resulting surviving fraction of individual cells, even though the radiation dose is the same. In general, survival rises to a maximum within 4 to 6 hours and levels off thereafter ( Fig. 1.12 ).
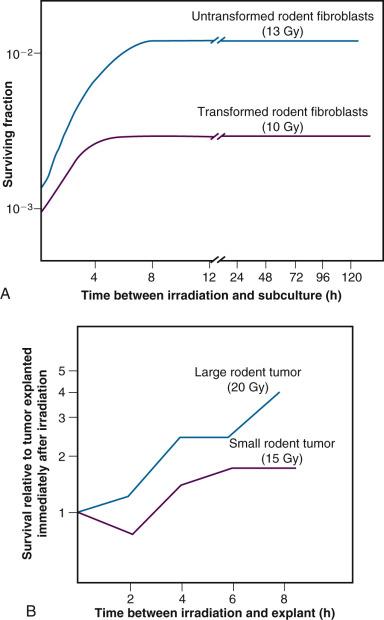
The kinetics and extent of recovery from both SLD and PLD are correlated with the molecular repair of DNA and the rejoining of chromosome breaks. For the purposes of radiation therapy, however, the most important consideration is that both processes have the potential to increase the surviving fraction of cells between subsequent dose fractions. Such a survival increase could be manifest clinically as either increased normal tissue tolerance or decreased tumor control. It is also important to appreciate that small differences in recovery capacity between normal and tumor cells after a single-dose fraction are magnified into large differences after 30 or more dose fractions.
When considering the repair phenomenon in intact tissues, it is important to remember that both the magnitude of the repair (related both to the shape of the shoulder region of the corresponding dose-response curve and the dose delivered) and the rate of the repair can influence how the tissue behaves during a course of radiation therapy. For example, a particular tissue—normal or tumor—may be quite capable of repairing most damage produced by each dose fraction, but if the interfraction interval is so short as to not allow all the damage to be repaired prior to the next dose, the tolerance of that tissue will be less than otherwise anticipated. Second, while the sparing effect of dose fractionation for both normal and tumor tissues can be explained largely by SLD recovery between fractions, at sufficiently small doses per fraction, the degree of sparing will reach a maximum below which no further sparing occurs, all other radiobiological factors being equal. This is a reflection of the fact that some radiation damage is necessarily lethal and not modifiable by either further fractionation or changing postirradiation conditions.
Become a Clinical Tree membership for Full access and enjoy Unlimited articles
If you are a member. Log in here